Research on modeling of nonlinear vibration isolation system based on Bouc-Wen model

Zhi-ling PENG*,Chun-gui ZHOU

College of Mechatronic Engineering,North University of China,Taiyuan 030051,China

Research on modeling of nonlinear vibration isolation system based on Bouc-Wen model

Zhi-ling PENG*,Chun-gui ZHOU

College of Mechatronic Engineering,North University of China,Taiyuan 030051,China

A feedforword neural network of multi-layer topologies for systems with hysteretic nonlinearity is constructed based on Bouc-Wen differential model.It not only refects the hysteresis force characteristics of the Bouc-Wen model,but also determines its corresponding parameters.The simulation results show that restoring force-displacement curve hysteresis loop is very close to the real curve.The model trained can accurately predict the time response of system.The model is checked under the noise level.The result shows that the model has higher modeling precision,good generalization capability and a certain anti-interference ability.

Bouc-Wen model;Nonlinearity;Vibration isolation system;Modeling

1.Introduction

The delay nonlinear systems,such as magneto-rheological damper,piezoelectric ceramic actuator and dry friction damping steel wire rope,exist in mechanical vibration isolation system,earthquake engineering,civil engineering,aerospace structural damping system,etc.Accurate modeling is an important prerequisite to the analysis and prediction of response of a dynamic system.It has been widely attention [1-3].Model is a widely used nonlinear phenomenological model[4].It describes smooth hysteresis behavior of lag element through the nonlinear differential equation.The nonlinear restoring force is divided into two parts:the frst part is the nonlinear an hysteretic restoring force only related to the instantaneous displacement and speed of the structure;the other part is pure lag restoring force related to the structure of the displacement time history,which can be described by frst order nonlinear differential equation[5-7].

In the paper,the Bouc-Wen model was used in the topology design of neural network layer.The corresponding relation of network weights and the model parameters was established.A neural network model was established through the network training,which can refect the hysteresis force characteristics of Bouc-Wen model and determine its corresponding parameters.

2.Mathematical model of hysteresis nonlinear system

In practical engineering applications,it is necessary to establish the mathematical description of hysteretic nonlinear force in order to analyze the hysteresis nonlinear dynamics system.Bouc-Wen differential model can describe the various forms of smooth hysteresis nonlinearity.As long as the parameters of the model are appropriately changed,it can describe the various types of hysteresis loops.Its expression is

whereR（t）is the restoring force of system lag;bx（t）is non-lag component;Z(t)is lag component.

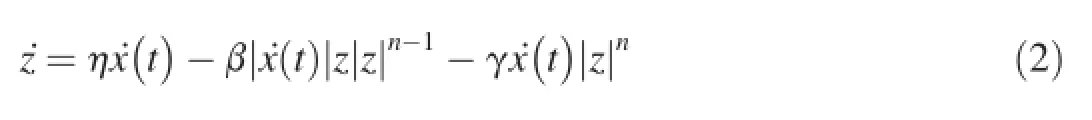
whereb,η,β,γ andnare the parameters to be identifed. Among them,b,η,β and γ control the shape of the hysteresis curve,andncontrols the smoothness of the transition zone in hysteresis curve.

Eq.(2)can be further rewritten as

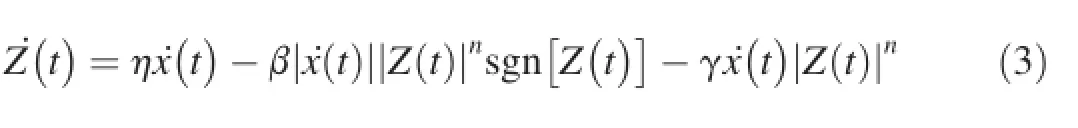
3.Modeling principle based on Bouc-Wen model

Bouc-Wen differential model refects the relation between the lag force and the displacement.As long as fve unknown parameters are obtained,the relationship between the restoring force and is determined[8,9].

According to the relation based on between restoring force and,by constructing a seriesofactivation functions, describing the differential equation by specifc neural network topology structure,correspond to the network weights and model parameters.A neural network model of the system lag resilience is established through the study of training of the custom network[10,11].The modeling principle is shown in Fig.1.

4.Neural network topology based on Bouc-Wen model

In order to construct a neural network topology,is obtained by discretized Eq.(1)

After frst order differential forward on Eqs.(2)and(3)can be

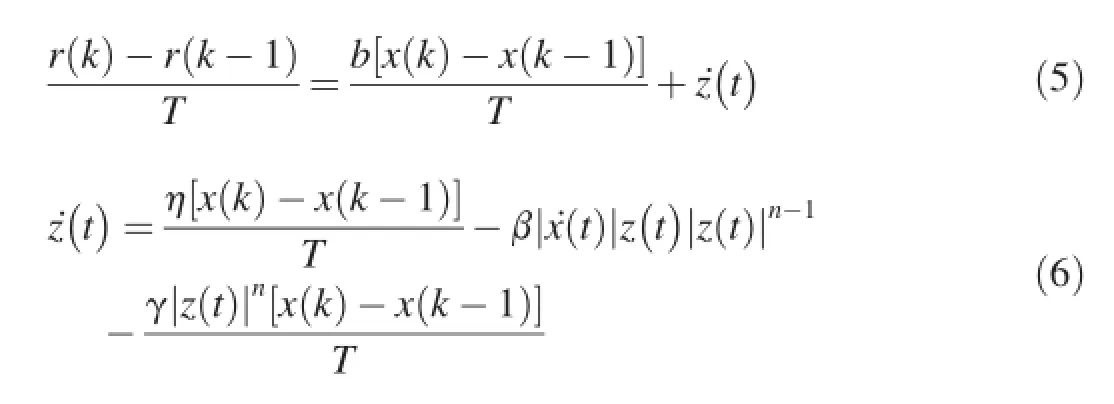
whereTis the sampling interval;k,k-1 are sampling time.

Eqs.(6)and(5)are combined together to gain a difference equation that indicates the relation between restoring force and displacement,and speed is

Fig.1.The principle of hysteresis nonlinear system modeling.

5.Establishment of neural network topology

According to Eq.(7),a neural network topology shown in Fig.2 can be established to achieve the hysteresis nonlinearity multilayer feedforward neural network modeling between restoring force and displacement.

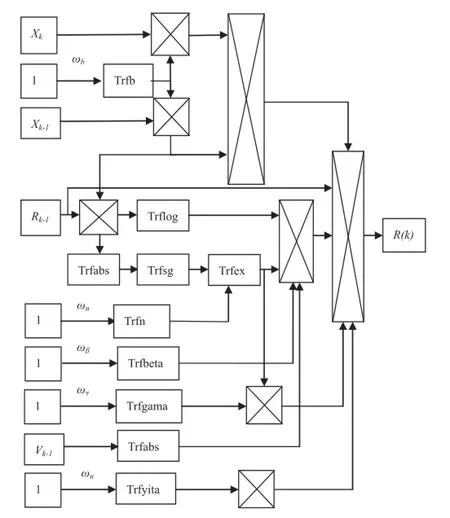
Fig.2.Multilayer feedforward neural network modeling.

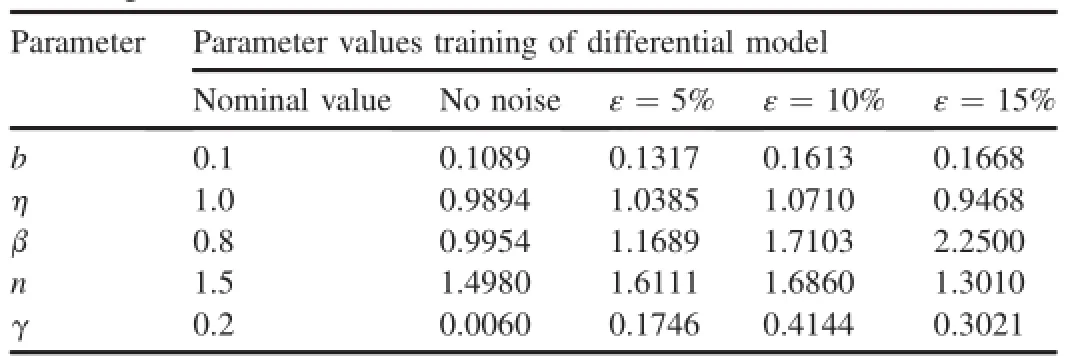
Table 1Modeling results of neural network based Bouc-Wen model.

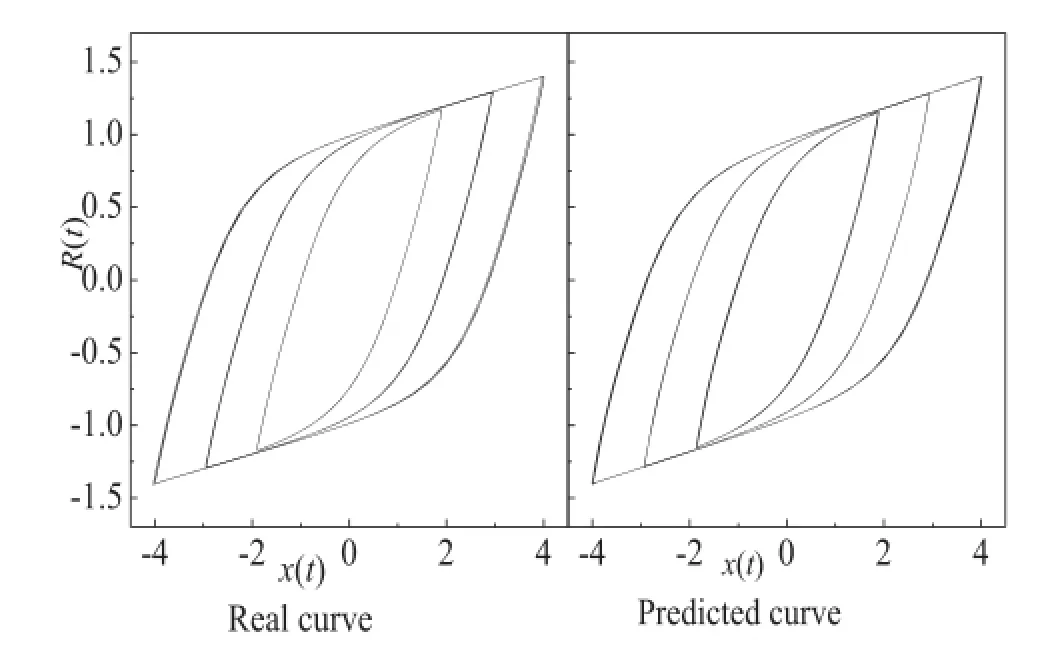
Fig.3.Horizontal excitation resilience-displacement hysteresis curves.

As shown in Fig.2,the model parameter information and structural information are embedded in the multilayer feedforward neural network which is integrated into the structure to be identifed as a priori knowledge of the model.In the MATLAB,acustom neuralnetwork isgenerated by net=network,called the init function,initializing the network with weights defned initialization function,to create hybrid network,training and learning,until it meets the requirements of training performance indicators.

6.Build neural network topology

Using the experimental data of three groups of response to custom neural network training fgure in Fig.2.Because the network created is static,training to learn through the improved BP algorithm[12,13].The parameter values of training results are presented in Table 1.In addition to the parameter γ,the other parameters are very close to the nominal values.

Fig.4.Comparison of steady-state responses under the three levels of motivation.

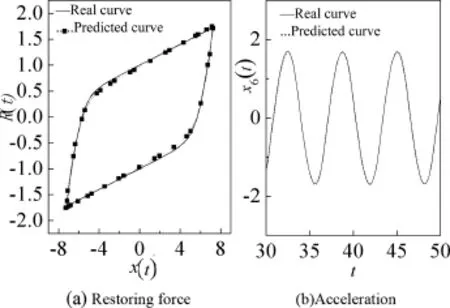
Fig.5.Hybrid models to predict compared with real response forXg4=6.0.

It can be found from Fig.3(a)and(b)that the restoring force-displacement hysteresis loop curve is very close to the real hysteresis loop curve.

In Fig.4,the comparison of the predicted steady-state responses of a real system under the three levels of motivation indicates that the training model can accurately predict the time response of the system.

To test the ability to promote the training of the hybrid network model,the predicted response is calculated and compared with the real response,as shown in Fig.5.The hybrid network model is still able to accurately predict the system response and the hysteresis curve,and has good generalization capability.

7.Model test in the presence of noise

Assuming that the restoring force data under the three levels of motivation is polluted by the noise,this is

whererjis the normal distribution with zero mean unit variance random signal sequence;Rj0is the magnitude of the restoring force;ε is noise level.

Fig.6.Hybrid models to predict compared with real response for ε=5%.

The hybrid network is trained in the use of data that ε is 5%,10%and 15%.The training parameters are listed inTable 1.When noise level is 5%,the training parameters have some deviation.But it can fnd that simulation model still can well predict the response of the system with hysteresis characteristics,as shown in Fig.6.In addition,the modeling results in Table 1 also indicate that the value of the error parameter training gradually increases with the increase in noise level. Then the effect of noise can be reduced by increasing the training sample data.

8.Conclusions

In the paper,a Bouc-Wen differential model of delay nonlinear systems was presented,a multilayer feedforward neural network model of neural network topology was constructed,and the model was trained and learning through experimental response data.The simulation results show that the restoring force-displacement hysteresis loop curve is very close to the real hysteresis loop curve,and the training model can accurately predict the time response of the system.It shows that the model has good generalization capability by comparing the predicted response with the real response.

[1]Tan Y,He Z,Gao JT.Isolation analysis of low-frequency vibration induced by high-speed railway.J South China Univ Technol(Natural Science Edition)2011;(6):132-6.

[2]Wen YK.Method for random vibration of hysteretic systems.J Eng Mech Div 1976;102(2):249-63.

[3]Fan YM,Li CJ.Non-linear system identifcation using lumped parameter models with embedded feedforward neural networks[J].Mech Syst Signal Process 2002;16(2-3):357-72.

[4]Ye Z,Sadeghian A,Wu B.Mechanical fault diagnostics for induction motor with variable speed drives using adaptive neuro-fuzzy inference system.Electr Power Syst Res 2006;76(9-10):742-52.

[5]Masri SF,Caffrey JP,Caughey TK,et al.Identifcation of the state equation in complex non-linear systems[J].Non-Linear Mechanics 2004;39:1111-27.

[6]Kovacic I,Brennan M,Waters T.A study of a nonlinear vibration isolator witha quasi-zero stiffness characteristic.JSoundVib2008;315(3):700-11.

[7]Ciarlini P,Maniscalco U.Wavelets and Elman neural networks for monitoring environmental variables. J Comput Appl Math 2008;221(2):302-9.

[8]Wang ZZ.The study of complex system modeling and simulation on evolution base.J Syst Simul(S1004-731X)2003;15(7):905-9.

[9]Li SH,Yang SP.Research status of hysteretic nonlinear models.J Dyn Control 2006;4(1):8-15.

[10]Lu JS,Fang R,Lan XJ.Hot research areas of simulation technique in the country-review of Journal of System Simulation in recent years.J Syst Simul(S1004-731X)2004;16(9):1910-3.

[11]Lou ML,Jia BY,Zong G,Shan TT.Measurement and analysis of subway-induced vibration of building with vibration isolation using continuous concrete wall.J South China Univ Technol(Natural Sci Ed 2013;(3):50-61.

[12]LuCH,BaiHB,YangJC,LiZZ.Researchonultra-low-frequencynonlinear vibration isolation system.2010.p.10-7(04).

[13]Chen BH,Woodley JM.Wavelet shrinkage data processing for neuralnetworksin bioprocessmodeling[J].ComputChem Eng 2002;26(11):1611-20.

Received 28 November 2013;revised 13 August 2014;accepted 13 August 2014 Available online 16 September 2014

*Corresponding author.

E-mail address:pengzhiling09@126.com(Z.L.PENG).

Peer review under responsibility of China Ordnance Society.

http://dx.doi.org/10.1016/j.dt.2014.08.001

2214-9147/Copyright©2014,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Copyright©2014,China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.