基于Pareto 蚁群算法的风电项目工期－成本－质量均衡优化

刘吉成，常 昊，王素花

(1．华北电力大学经济与管理学院，北京市102206;2．大唐三门峡电力有限责任公司，河南省三门峡市472143)

0 引 言

目前国内风电行业正在经历漫长而又痛苦的结构调整期，行业困境日益凸显，企业生存能力大幅削弱，尽管享受着来自国家层面的各项补贴，但风电企业发展的黄金周期已经过去。若将风电基地的建设、运营、并网工作做好，风电行业过剩产能就能在相对较短的时间内得到有效消化，而结构失衡、市场在外、企业盈利能力低下等问题也会得到缓解。

任何项目的基建期都需要考虑工期、成本和质量3个主要因素，风电项目基建也不例外，自始至终都是以工期－质量－成本这条主线开展各项工作的。风电工程建设期一般为1年，在相对较短的建设期内，机组基础混凝土施工、升压站建筑、设备安装调试、线路工程等众多分项工程可能需要同时展开施工，各环节衔接配套关系紧密［1］。但是，很多风电项目工期拖延严重，成本难以控制，质量难以保证。因此，风电项目工期、成本和质量的均衡优化是风电项目基建期的重点工作。

工期－成本－质量均衡优化问题一直是国内外学者研究的热点，很多文献都对这方面做了深入的研究。文献［2－4］分析了工期－成本－质量的关系，文献［5－7］分别利用模糊算法、随机算法和整数规划算法对工期－成本进行了均衡优化，文献［8］利用非支配排序遗传算法对工期－成本－资源进行了综合优化。关于风电项目的研究主要侧重于前期投资决策方面［9-10］，目前关于风电项目基建期工期－成本－质量优化的研究很少。

基于此，本文在分析风电项目工期－成本－质量关系的基础上，从效用函数的角度，利用多目标优化Pareto 蚁群算法对风电项目基建期的工期－成本－质量进行均衡优化。

1 风电项目工期－成本－质量关系

风电项目基建期施工环境比较恶劣，相邻风机间间距较大，作业范围广，隐蔽工程较多。风电场的建设大多处于边远地区。风电工程的里程碑节点如表1 所示。从表中可以看出风电项目施工有11个里程碑节点，第1 ～9个节点与工期－成本－质量息息相关，是基建期不容忽视的环节。每个节点又由多个工序组成，每个工序的管理都涉及到3个方面即工期、成本、质量，工序的持续时间决定了该节点的完成时间和下一个节点的开始时间，各个工序的持续时间不同，其成本和质量也不同。

表1 风电工程里程碑节点Tab.1 Milestone nodes of wind power project

2 风电项目工期－成本－质量均衡优化模型的建立

2.1 决策变量

在风电项目建设过程中，各工序的持续时间可以根据人力、物力等资源的变化而缩短或延长。各工序不同的持续时间会对整个项目的工期、成本和质量产生影响，为了得到最优的选择方案，本文将工序的实际持续时间、成本、质量作为决策变量。

2.2 效用目标函数

2.2.1 工期效用函数

对于工程项目每个确定的施工方案，各个工序的持续时间是确定的，工期的效用值为各个工序持续时间的效用值和，在一定的工序持续时间范围内，工期效用函数如式(1)所示。工期效用函数是在工程中所获得的效用与工序时间分配之间的数量关系。

式中:U(t)为工期的效用值;ti为工序i 的实际持续时间;t1i为工序i 的最短持续时间;t2i为工序i 的最长持续时间;ai为工序i 效用系数;u 为工序数量;U 为全部工序的集合。

2.2.2 成本效用函数

风电工程项目的建安成本由直接成本和间接成本组成。其中，直接成本是指直接用于生产过程的各项费用，包括人工费、材料费、机械台班费等;间接成本包括对项目进行管理、审查等工作的费用。成本的效用值为各个工序成本的效用值和，在一定的成本范围内，成本效用函数如式(2)所示。成本效用函数是在工程中获得的效用与所需的成本费用之间的数量关系。

式中:U(c)为成本的效用值;ci为工序i 实际持续时间下的成本;c1i为工序i 的最小成本;c2i为工序i 最大成本;δi为成本效用函数的系数;θi为成本的固有效用值。

2.2.3 质量效用函数

风电工程质量是由施工过程中的工序质量决定的。每一道工序的质量好坏，最终都会直接或间接地影响工程质量，所以工序质量是形成工程质量最基本的环节。质量的效用值为各个工序质量的效用值和，在一定的质量范围内，质量效用函数如式(3)所示。质量效用函数是指在工程中获得的效用与工程达到的质量标准之间的数量关系。

式中:U(q)为质量的效用值;qi为工序i 实际持续时间下的质量;q1i为工序i 的最劣质量，即经质量评定后的最低分值;q2i为工序i 最优质量，即经质量评定后的最高分值;ηi为质量效用函数的系数;ρi为质量的固有效用值。

2.2.4 工期－成本－质量均衡优化模型

通过建立工期效用函数、成本效用函数、质量效用函数，可以得知工期最短的时候，成本不是最小，质量也不是最优，如何使得三者之间达到Pareto 最优，需要建立风电工程项目工期、成本、质量多目标优化模型，具体如下:

3 模型求解的Pareto 蚁群算法

Pareto 蚁群算法(Pareto ant colony optimization，PACO )是一种多目标单种群蚁群算法［11-12］。与单目标蚁群算法最大的不同就是各条路径上对应k个目标有k个信息素，用信息素向量τki表示。在每只蚂蚁构造解的开始阶段随机确定k个目标的权重ωk，其中0 ≤ωk≤1，

Pareto 蚁群算法采用伪随机比例规则选择下一路径，即设定一个常数ξ0，生成一个在［0，1］上均匀分布的随机变量ξ，如果ξ ≤ξ0，则选择式(5)，否则选择式(6)。

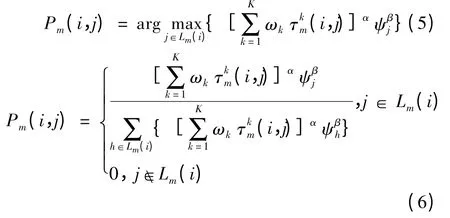
式中:Pm(i，j)代表蚂蚁m 第i 步选择前进路径j 的转移概率;Lm(i)代表蚂蚁m 第i 步所能选择的所有前进路径;τkm(i，j)代表蚂蚁m 第i 步所选择的路径j 上对应目标k 的信息素向量;表示路径j上信息素向量的加权和;为能见度因子;α 反映了蚂蚁在运动过程中所积累的信息在蚂蚁选择路径中的重要性;β 反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的重要性。

每1 只蚂蚁完成1次搜索时，进行信息素强度的局部更新。如果路径(i，j)是蚂蚁m 所选择的前进路径之一，则按式(7)更新信息素强度:

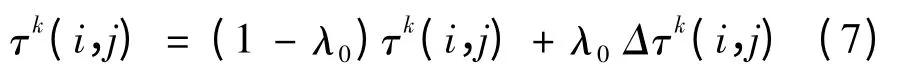
式中:0 ≤λ0≤1 为常数，(1 －λ0)τk(i，j)代表信息素的挥发。

所有蚂蚁均完成1次检索时，对于当前最优方案上的路径，按式(8)进行全局信息素更新:

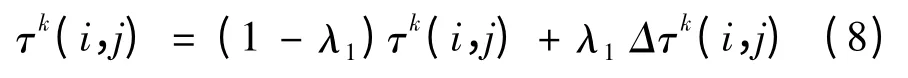
对其他路径，按式(9)进行全局信息素更新:

式中:0 ≤λ1≤1 为常数，(1 －λ1)τk(i，j)代表信息素的挥发。

4 实证分析

4.1 风电项目概况

假设某风电工程项目施工网络计划如图1 所示。各工序的最短持续时间、最长持续时间、成本、质量、效用系数等参数数据如表2 所示。

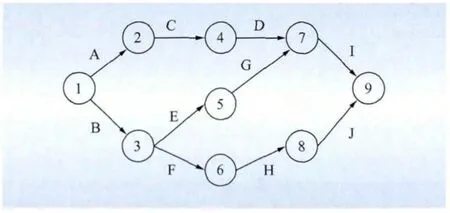
图1 某风电工程项目施工网络计划图Fig.1 Construction network plan of a wind power project

表2 风电项目相关参数及数据Tab.2 Related parameters and data of wind power project

4.2 模型求解

由图1 可以计算得出该风电工程项目的关键路径为A-C-D-I，工期的变化范围为65 ～90 天。本文采用Pareto 蚁群算法求解风电项目基建期工期－成本－质量均衡优化模型。本项目共10个工序，因此为10 维的列向量，蚂蚁个数设为20个，ψj，α，β 参数均取1，工期效用目标、成本效用目标、质量效用目标对应的信息素分别为:τ1(i，j)，τ2(i，j)，τ3(i，j)。

在蚂蚁每次构造之前，随机确定工期效用目标权重ω1(0 ≤ω1≤1)，成本效用目标权重ω2(0 ≤ω2≤1，质量效用目标ω3= 1 － ω1－ ω2)。

对于局部信息素更新，式(7)中的Δτk(i，j)选取规则为:

式中:local1，local2，local3 为常数;u(t)，u(c)，u(q)分别为第m 只蚂蚁选择的方案按式(1)，(2)，(3)所得的效用目标函数值。

对于局部信息素更新，式(8)中的Δτk(i，j)选取规则有2 种。

(1)只更新当前Pareto 前沿中目标函数(1)，(2)，(3)的最大值所选择的路径上的信息素:

(2)只更新当前Pareto 前沿中综合目标最大值所选择的路径上的信息素:

式中:global1，global2，global3 为常数;max u(t)，max u(c)，max u(q)和max u(t，c，q)分别为当前Pareto 前沿中效用目标函数(1)，(2)，(3)和综合目标的最大值。

PACO 有关参数设置为:初始信息素设为1，ξ0=0.5，λ0=0.1，λ1=0.1，local1 =0.9，local2 = 0.8，local3 = 0.7，global1 =1，global2 =0.9，global3 =0.6，迭代次数为400，用MATLAB 编写Pareto 蚁群算法(PACO)程序进行求解。

4.3 结果分析

通过运行结果可以得出该风电工程项目进行工期－成本－质量多目标优化后的部分Pareto 最优解集和Pareto 前沿如图2 所示。从图2 中可以看出，通过Pareto 蚁群算法得到的目标值比较理想，工期效用、成本效用、质量效用这3个目标值达到了Pareto最优。

部分Pareto 解及其对应的工期－成本－质量效用值如表3 所示。将工期拆分为各个工序的持续时间，综合目标最优时，对应的各个工序的Pareto 解如表4 所示。表3、4 为决策者提供了决策依据，决策者可以根据其对工期、成本、质量的偏好程度确定每个工序的持续时间、成本与质量。

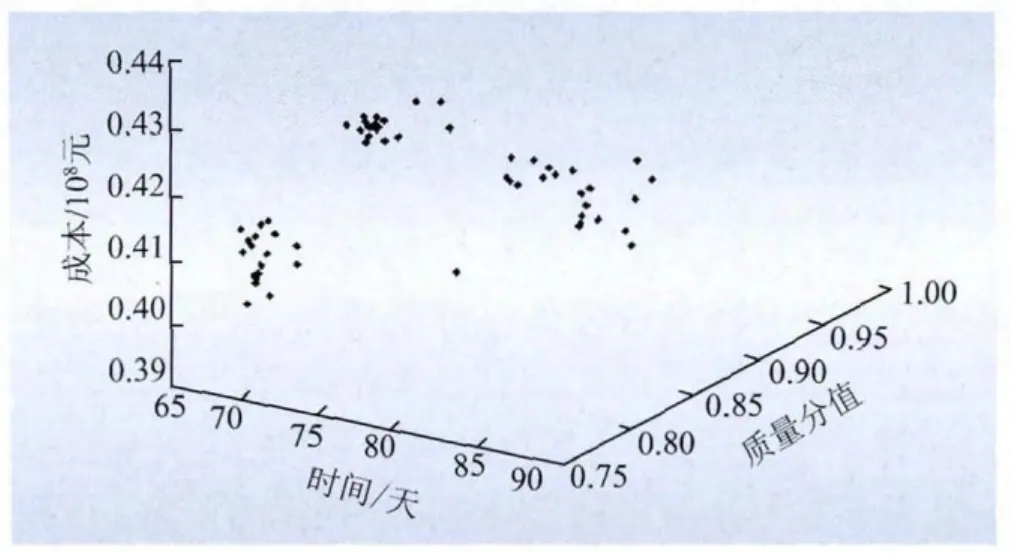
图2 工期－成本－质量效用的Pareto 前沿Fig.2 Pareto frontier of time-cost-quality utility

表3 工期、成本、质量效用目标值及其pareto 解Tab.3 Time-cost-quality utility objective values and Pareto solution

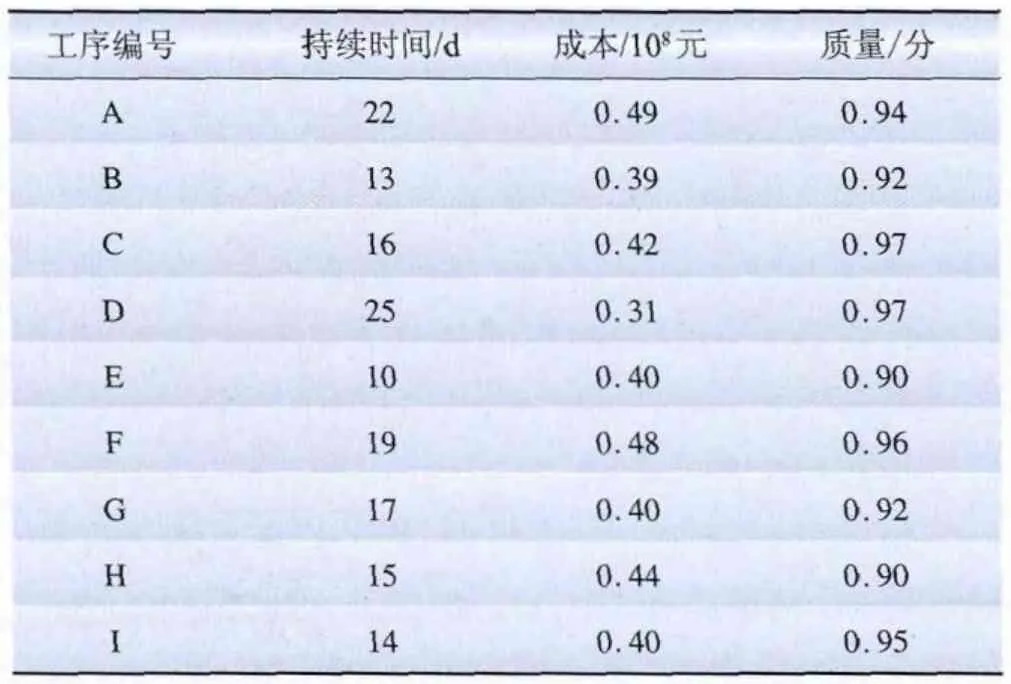
表4 工期—成本—质量效用最优时对应的工序pareto 解Tab.4 Pareto solution of working procedure when time-cost-quality utility is optimal

5 结 语

破解风电建设难点的当务之急就是开展风电项目管理的研究［13-14］。本文针对风电工程项目基建期的实际问题，在对风电工程项目中工期－成本－质量的关系分析的基础上，运用效用函数思想，构建了风电项目工期—成本—质量均衡优化模型，采用多目标优化算法Pareto 蚁群算法，得到一组Pareto 最优解，并生成三维pareto 图，不仅验证了该优化模型的可行性，还更直观地为管理者提供了决策依据，具有一定的理论意义和实践意义。本文是采用Pareto 蚁群算法在风电项目工期－成本－质量中的初探，在优化过程中没有将项目管理中的四大因素之一——安全目标考虑进去，在后续的研究中将加入安全目标，这样会更符合工程实际。

［1］王勇．风电工程建设中的管理模式及风险因素分析［J］． 风能，2010，(9):34-37．

［2］Tareghian H R，Taheri S H． On the discrete time，cost and quality trade-off problem［J］． Applied Mathematics and Computation，2006，181 (2):1305-1312．

［3］Chen C H，Chong Y T，Chang W C，et al． A quality – time –cost-oriented strategy for product conceptualization［J］． Advanced Engineering Informatics，2012，26(1):51-52．

［4］代逸生，刘媛． 基于MCCAA 的工期成本质量的多目标优化分析［J］． 科学技术与工程，2012，12(19):4676-4680．

［5］Eshtehardian E，Afshar A，Abbasni R，et al． Fuzzy-based MOGA approach to stochastic time-cost trade-off problem［J］．Automation in Construction，2009，18(5):692-701．

［6］Yang． I T． Stochastic time-cost tradeoff analysis:A distribution-free approach with focus on correlation and stochastic dominance［J］．Automation in Construction，2011，20(7):916-926．

［7］Szmerekovsky J G，Venkateshan P． An integer programming formulation for the project scheduling problem with irregular time–cost tradeoffs［J］． Computers ＆Operations Research，2012，39(7):1402-1410．

［8］Ghoddousi P，Eshtehardian E，Jooybanpour S，et al． Multi-mode resource-constrained discrete time – cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm［J］． Automation in Construction，2013，30(1):216-227．

［9］Janss G F E，Lucas M，Whitfield D P，et al． The precautionary principle and wind-farm planning in Andalucia［J］． Biological Conservation，2010，143(8):1827-1828．

［10］Muthuselvan N B，Devesh R M，Somasundaram P． Cauchy-Gaussian Infused Particle Swarm Optimization for Economic Dispatch with Wind Power Generation［J］． International Review of Electrical Engineering-IREE，2011，6(1):387-395．

［11］Xu R，Chen H P，Li X P． A bi-objective scheduling problem on batch machines via a Pareto-based ant colony system ［J］．International Journal of Production Economics，2013，145 (1):371-386．

［12］Doerner K F，Gutjahr W J，Hartl R F，et al． Pareto ant colony optimization with ILP preprocessing in multiobjective project portfolio selection［J］． European Journal of Operational Research，2006，171(3):830-841．

［13］靳丹，何世恩，丁坤． 关于大规模风电基地建设的思考［J］． 电力建设，2011，32(10):63-65．

［14］盛大凯，仇卫东，齐立忠． 实现风电发展“五个转变”的有效途径［J］． 电力建设，2011，32(11):6-9．