考虑电价－出力关联不确定性的风电场投资分析

曹银利，刘继春，张 放，邓 创，王 玮，陈振寰，张 鹏

(1．甘肃电力调度通信中心，兰州市730050;2．四川大学电气信息学院，成都市610065;3．四川省电力公司电力应急中心，成都市610041)

0 引 言

近年来，风能作为一种无污染的可再生能源得到了快速的发展，风电的投资规模也不断增加。然而，风力发电的可控性差，与传统电网的协调性能低，造成风电资源的闲置和浪费，制约着风电及其电网的可持续发展。在风电大规模并网之后，电网投资不仅仅只有负荷、潮流变化等传统的不确定性，风电资源的随机性对电网投资的影响也日渐明显。

目前，对电网投资组合及投资风险分析已有大量研究。文献［1］综合考虑了电网建设项目的社会性和可靠性，选取容载比量化投资可靠性，建立电网最优投资组合模型。文献［2-3］从成本和收益的角度，引入集对分析理论处理电网规划中的不确定因素，构建了电网投资的成本－效益净现值的决策评估模型。文献［4］通过情景模拟，根据投资组合的风险分散化原理，建立了基于条件风险价值的动态多阶段资产配置模型，分析了不同资产调整策略对资产配置效果的影响。上述文献均没有定量地考虑风电资源的不确定性对电网投资的影响。文献［5］从风能资源的充分利用和环境价值两方面出发对风电场的选址及布局做了规划，但并未计及风电场的建设成本和风电容量的分配。文献［6］引入“能源环境效益”的概念，建立了环境效益好，资源消耗少，系统安全性高的多目标优化调度模型。文献［7］利用投资组合理论，构建以常规机组投资成本低和风电并网后投资组合风险小为目标的投资组合模型，但其求解相对较复杂。

电力市场中，电价的强波动性和风能资源的随机特性，使估计风电场的投资效益变得困难，因此寻找有效方法评估潜在的投资风险，减少经济损失显得尤为重要。利用现代投资组合理论指导风电场投资，可以在可承受风险范围内大大提高投资收益。然而风电场实测数据庞大，求解过程计算量大，为了在保证精度的同时有效地减小计算量，采用粒子群算法求解优化模型，得到最优风险组合方案。本文分析风电出力与电价的关联不确定性，利用风险投资组合理论建立风电场年收益风险评估模型;根据投资组合理论研究不同风电场之间的关联关系，定量研究风电场集群收益特性及其风险评估;设定可承受风险阈值，利用粒子群算法求解模型，以验证风电集群效应在减小投资风险上的有效性，为投资者提供有价值的参考方案。

1 计及不确定性的风电场组合投资分析

风电场的年收益主要由风电出力及其电网收购价格决定。风电出力的间歇性、波动性和不可控性，电价的不确定性使得风电投资面临着风险。本文先讨论在电价和出力关联不确定性的影响下，根据投资组合理论，用方差或标准差来表征风电场年收益的投资风险。

1.1 单个风电场的年收益期望和方差

设某地区风电场个数为N，收购电价为λh，风电场每h 出力为Ph，则单个风电场每h 的收益可以表示为［8-9］

风电场年收益是每个结算期收益(1 h 为1个结算期)的连续相加，则年收益期望可表示为

对于风电场年收益期望计算，价格λh和出力Ph均呈现出周期性的变化，根据计量经济学中相关知识可知，估计收益期望时可通过一个中间变量来消除可观测变量的周期性典型波动变化的影响［10］。假设风电场出力及其价格在1年中每1个月的每1 天中的相同时段具有相似的波动规律，这个时段称为典型波动时段，则1年共有k = 12 ×24个= 288个典型波动时段。设矩阵S 为所需的中间变量矩阵，S = (s1，s2，…，sk)，其中sk为一个8 760 ×1 列向量。对sk的确定有以下说明:s1中的元素从1月的1:00 开始到12月的24:00 依次编号，当元素所在位置刚好为1月的1:00时元素就为1，即1月1 日1:00，1月2 日1:00，…，1月31 日1:00 所对应位置的元素值为1，其余位置为0。s1～s24分别为1月的24个时段所对应的向量，其余依此类推。基于中间变量矩阵计算的价格可表示为

式中λ 为由对应的典型波动时段的价格期望组成的向量，λ = (λ1，λ2，…，λ288)T。同理，基于中间变量矩阵计算的风电场出力为

式中P 为由对应的典型波动时段的出力期望值组成的向量，P = (P1，P2，…，P288)T。此时，年收益期望计算式为

令式(5)中STS = m，计算可知矩阵m 为一对角阵，且主对角线上元素正好为每个月的天数。

根据式(3)～(6)可得:

由式(1)和概率统计相关知识可知，第k个典型波动时段的收益方差为

式中:λk、Pk分别为第k个典型波动时段的收购电价和风电场出力期望值。

由于风速在时间尺度上几乎是连续变化的，风速的观测值相对靠近观测前一时段的几率很大，所以对于各个时段的风速观测值存在自相关性。由此可知风电场时段间的出力也不是完全独立的，存在着一定的相关性，因此风电场年收益的方差并不是多个时段独立收益方差的简单相加，还包含时段收益间的自相关方差。时段间的自相关方差计算公式为

式中:ρij为时段(i，j)的相关系数;δ2(Ri)、δ2(Rj)分别为第i 时段、第j 时段的收益方差。

设矩阵Δ 是以δ2(Rk)为主对角元素的对称矩阵，则

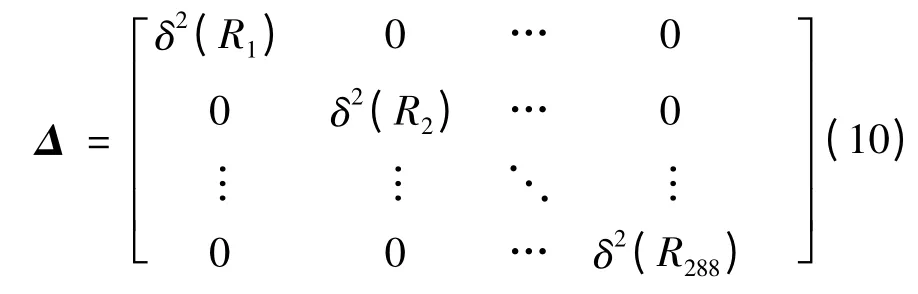
由式(7)～(10)可得年收益方差为

式(11)中，当i 属于第k个典型波动时段时，δ2(Rk(i))= δ2(Rk);同理，当j 属于第k个典型波动时段时，δ2(Rk(j))= δ2(Rk)。

1.2 风电场组合的投资风险分析

在第1.1 节的分析中，得到单个风电场的投资风险。投资时，投资者在规避高风险的同时争取高额利润，投资组合理论表明投资组合的风险比单个资产风险小，并且当资产间收益率的波动规律相反时，可能出现零风险的情况，因此对多个风电场的投资比例分配以及组合投资的意义巨大。下面将对风电场投资组合风险进行分析。

某区域有N =10个风电场，若投资者选择n个风电场作为投资，则共有种组合方式，这些组合方式构成投资决策集合。设对第i个风电场投入的资金比例为xi，则

由投资组合理论可知第j 种组合的组合年收益为

组合年收益期望为

组合年收益方差为>

式中:vil为风电场组合(i，l)的年收益协方差;为独立风电场i 的年收益方差。

实际投资中需要得到多个风电场的最优投资比例，如果要得到最优化的投资组合方案，则需要在建立投资模型后对模型求解。拟建风电场多年实测数据繁多，由此模拟出来的风机出力数据也十分庞大，如果按照传统方法求解则计算过程十分复杂。为了在保证精度的前提下快速求解模型，得到最优化投资组合方案，本文采用粒子群算法求解风险投资组合模型。投资者可以根据自身的风险承受能力决定承担多大的风险，通过优化配置获得相应的收益奖励。

2 风电场投资组合模型建模及求解

2.1 风电场风险投资建模

在一定风险阈值下，风电场投资组合模型为

式中:R 为独立风电场年收入期望矩阵;x 为各个风电场投资比例;v 为年收入协方差矩阵，其元素vil可通过式(11)～(14)得出;δ2为风电场年收入方差的设定阈值，即能接受的最大风险;L 为风电场配置比例下限;U 为风电场配置比例上限。

2.2 基于粒子群算法的模型求解

在对风电场进行分析时，由于数据庞大，按照传统的求解风险投资组合方式，计算量大，过程复杂，耗时多，收敛速度慢。因此，本文将采用粒子群算法求解模型，可以在短时内收敛，寻求到全局最优解。

粒子群优化算法(particle swarm optimization，PSO)作为一种人工智能算法，在电力系统中已经得到非常广泛的应用。其迭代公式为

式中:β 为粒子的惯性权重，用来调整粒子的搜索速度;vid(t)为粒子i 的第d 维在第t次迭代时的速度;xid(t)为粒子i 的第d 维在第t次迭代时的位置;r1、r2为［0，1］之间均匀分布的随机数;c1、c2为学习因子，c1、c2≥0，代表将每个粒子推向个体历史最优位置和群体历史最优位置;Pid为每个粒子本身的最优解;Pgd为整个种群目前找到的最优解，即所有粒子中位置最佳的一个。

利用粒子群算法求解风电场风险投资模型，则每个粒子位置的每个维度代表各个风电场资源配置比例，即最终所求的投资方案;粒子的适应度代表目标函数，个体适应度Pid代表该粒子从开始搜索到当前所求得的最优适应度，全局适应度Pgd代表全体粒子从开始搜索到当前所求得的最优适应度。

基于粒子群算法的风电场风险评估模型求解步骤如下:

(1)输入风电场风险投资计算所需的历年数据，根据风速数据及风功曲线估算风机出力，计算独立风电场每MW 装机年收入期望和标准差。

(2)初始化粒子群N，粒子位置xi的每一维代表风电场的资金配置比例，粒子速度vi随即初始化。

(3)根据粒子的位置xi，即各个风电场资金配置比例，计算投资风险，如果风险大于设定阈值则重新生产粒子。

(4)计算函数适应度，求出当前全局最优值，如果满足阈值或者迭代次数超过设定值则结束迭代，不满足要求则更新粒子的速度vi和位置xi，进入迭代循环。

模型求解流程如图1 所示。

图1 模型求解流程Fig.1 Flow chart of model

3 算例计算

本文采用某地区近几年的风电场数据进行仿真分析。根据我国风电实行标杆电价的政策，设风电的价格为一固定值λ =0.45元/(kW·h)，δ 取为独立风电场年收入标准差的平均水平。仿真中c1取1.5，c2取2，β 取0.5，L 取0，U 取1，粒子位置和初始速度均随机初始化。为了消除风电场装机容量各不相同造成无法评价比较的情况，将单位装机容量产生的年收入期望和年收入标准差进行比较。收集拟建设的风电场风速数据及风功曲线估算风机出力，在此基础上计算得到独立风电场每MW 装机年收入期望和标准差，结果如表1 所示。

表1 独立风电场年收入期望和标准差Tab.1 Annual income expectations and standard deviation of independent wind farm

图2 是约束条件下的投资目标函数变化趋势。由图2 可见，在第5次迭代时目标函数收敛达到了全局最优值115.71万元，此时代表投资风险的年收益标准差为8.78万元。

图2 函数适应度曲线Fig.2 Fitness curve

表2 为目标函数达到全局最优时各个风电场投资配置比例。

表2 各个风电场投资配置比例Tab.2 Allocation weights of each wind farm

优化资源配置后投资获得的年收益达到了115.71万元的高值，虽然比8 号风电场单独运行时稍低，但是风险却大大降低，低于投资单个风电场时风险最小值2.7%，相比其他风电场单独运行时年收入期望也提高了很多。由此可见基于粒子群的风险投资方案能在可控风险范围内有效提高投资收益，投资者可以根据自己的风险承受能力和投资偏好设置风险阈值，加入相应约束条件。

4 结 论

(1)本文在分析了风电价格和出力关联不确定性的基础上，应用投资组合理论建立风电场投资风险评估方法。通过比较单个风电场和风电场组合投资的收益和风险，验证了风电场组合投资的收益比构成组合的单个资产收益大，而相应的风险却减小很多，直观地说明了投资组合的意义。

(2)采用粒子群算法求解风险投资组合模型，能快速得到收敛解。由仿真可知，利用风险投资理论优化配置资源可以在保持投资收益高的同时大大降低投资风险;相对于单独投资某个风电场，在风险可承受范围内投资收益更令投资者满意。

(3)当2个风电场的相关系数为负时，波动具有一定程度相反趋势，形成互补，更加有效地降低风险。投资者在建立风险投资模型时可以根据自己的期望收益或风险承受能力设定阈值，求解模型。

［1］董军，马博． 考虑社会效益的电网最优投资组合模型研究［J］． 运筹与管理，2010，19(4):131-135．

［2］谢敬东，王磊，唐国庆．集对分析评价法及其在电网规划中的应用［J］．电网技术，2002，26(11):37-40．

［3］王绵斌，谭忠富，张丽英，等． 市场环境下电网投资风险评估的集对分析方法［J］．中国电机工程学报，2010，30(19):91-99．

［4］赵文会，王炜，施泉生，等．基于条件风险价值的动态对阶段电力资产配置模型［J］．电网技术，2009，33(7):77-82．

［5］乔歆慧，张延迟，解大．风电场的选址及局部优化仿真［J］．华东电力，2010，38(6):934-936．

［6］陈道君，龚庆武，张茂林，等． 考虑能源环境效益的含风电场多目标优化调度［J］．中国电机工程学报，2011，31(13):10-17．

［7］曾鸣，张徐东，田廓，等．考虑风电并网的发电容量投资组合优化模型［J］．电网技术，2011，35(12):153-159．

［8］Edwin J E，Martin J G，Stephen J B，et al． Modern portfolio theory and investment analysis［M］． John Wiley ＆Sons，Inc，1991:45-66．

［9］．Gomez C Q，Hugo A G． Price and resource-related uncertainty in the estimation of the revenue of a wind farm［J］． IEEE Trans on Power Systems，2011，26(4):2074-2083．

［10］Davidson R，Mackinnon J G． Econometric theory and methods［M］． New York:Oxford Univ，Press，2004．