快速解列判据在多通道互联电网中的应用研究

俞璐，武群丽，杨雨昂，杨明玉

(华北电力大学，河北省保定市071003)

0 引言

近年来，全国联网、“西电东输”和“南北互供”等战略的实施，特高压交直流输电线路的投入使用，光伏、风力发电等新能源大量接入电网，使得我国电力系统得到了进一步发展，同时大电网的结构越来越复杂，这必然使电网的安全稳定控制面临着更高的挑战。许多大电网由于存在严重的安全防御系统隐患，一旦遭遇无法预料及连锁发生的偶然事件，很有可能导致重大事故，其影响波及面将更加广泛，不仅会造成巨大经济损失，还有可能影响人们的正常生活，甚至造成社会混乱［1-5］。不过，从电力系统发生故障到大面积停电往往都要经历一个较长的演变过程，如果能够采取快速有效的控制措施，大停电事故是有可能控制和避免的。

失步解列作为针对罕见的严重复杂故障的第3道防线的控制措施，能够有效避免事故扩大可能导致的长时间、大范围停电和系统崩溃，并尽量减少负荷损失，以免造成巨大经济损失和社会影响，因此在我国得到了广泛的应用。

目前国际上失步解列研究的发展趋势是，研究基于就地信号进行失步判断的新算法，和基于同步相量测量技术的自适应失步解列装置。国内目前的失步解列装置除采用传统的失步判别算法，例如阻抗继电器法和角度变化法外［6-8］，还有根据输电线路功率的变化趋势、线路两端电压相角差的变化趋势，以及系统振荡中心的位置等因素，预测系统失步的快速解列装置［9］。

经理论和实践验证，快速解列装置的判据对于具有单失步通道(大区之间失步联络线路)的电力系统是严格且有效的，但对于具有多通道的复杂电力系统，由于各通道参数变化具有不同时性，快速解列装置是否仍然能够有效解列各通道，这是个需要研究的问题。本文将以三机系统为例，通过对三机振荡中心发展机理的分析，研究快速解列判据在复杂多通道电力系统应用的有效性。同时，通过实际系统仿真计算，验证本文的研究结论。

1 快速解列装置原理简介

PAC-1000电力系统失步快速解列装置，根据输电线路功率的变化趋势、线路两端电压相角差的变化趋势以及系统振荡中心的位置等因素，来形成失步解列判据［10-11］。系统在由同步运行状态向异步运行状态转移过程中，线路两侧的电压功角差以加速度增加，但线路有功功率不断减少，当振荡中心进入装置保护范围内且振荡中心的电压低于门槛值时，装置即发出解列启动信号。

PAC-1000电力系统失步快速解列判据如下:

(1)ECS，振荡中心在本线路上;

(4)UECS＜USET，振荡中心电压小于门槛值。

本失步解列判据主要具有以下特点:(1)快速，可以在系统第1个异步运行周期内发出解列信号;(2)准确，可以确定振荡中心的位置，在振荡中心所在的断面将系统解列;(3)简单，判据运算所需的信号仅为装置安装点的线路电压和线路电流信号，不需要其他辅助信号和远方信号。但这一组判据只是基于单通道简单系统提出来的，在具有多通道联络线的复杂电力系统上的应用以及通道间相继解列的相互影响并未有任何文献考虑到其适用性。

2 快速解列判据在多通道失步时有效性分析

多机电力系统与简单两机系统的不同在于失步振荡时电气量变化更加复杂，由于各线路参数变化具有不同时性，同一失步断面各个通道存在不同时解列情况。若某一通道先出口解列，其他通道判定失步与否过程中是否会受到影响，以下将以三机系统为例，通过分析本系统两失步通道在失步振荡时功角、角速度及电磁功率的变化特征，研究快速解列判据在多通道情况下的适用性。

2.1 三机系统解列情况分析

三机系统如图1所示。假设L1－2－1故障断开导致线路重载进而失步。由于大量理论和实践经验表明，在系统第1失步周期，往往形成2个失步机群，现假设机组G1为一同调机群，剩余机组为另一同调机群。显然，在这种假设情况下失步断面如图1所示，失步通道是联络线L1－2(L1－2－2)和L1－3。现分析这2条通道是否满足判据要求。

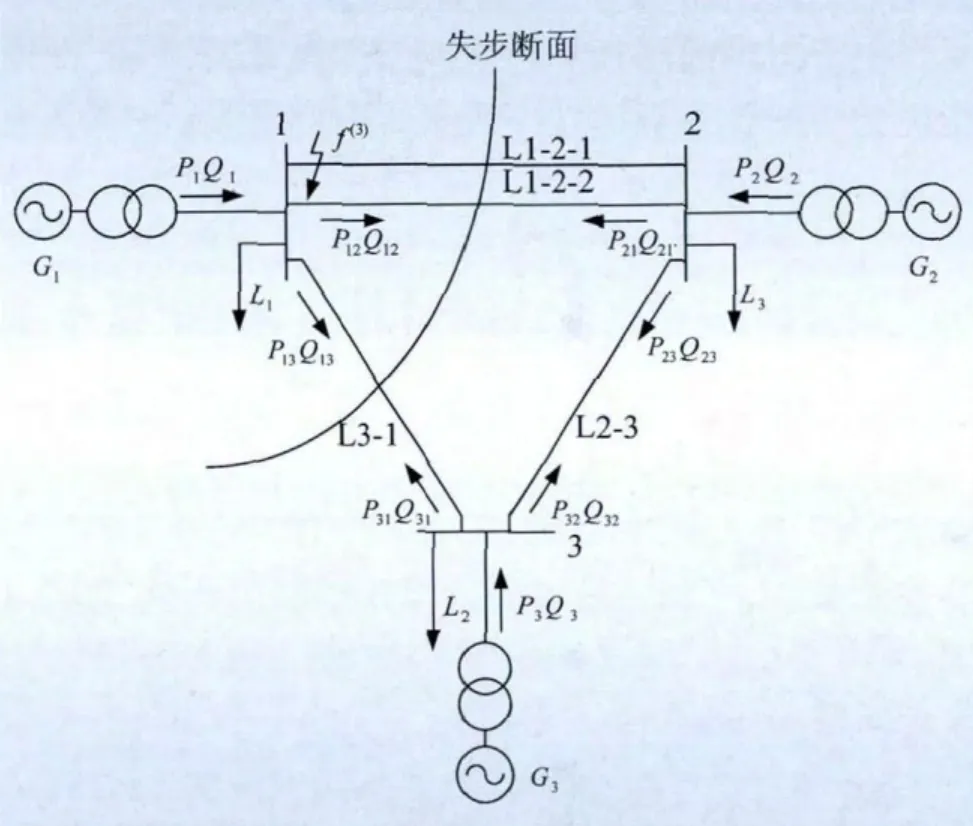
图1 三机系统模型Fig.1 Three-machine system model

机组G1的转子运动方程为

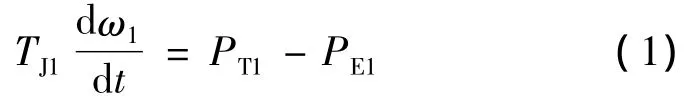
式中:TJ1为机组G1的惯性时间常数，s;ω1为机组G1的角速度，标幺值;PT1为机组G1的机械功率，标幺值;PE1为机组G1的电磁功率，标幺值。

由文献［12］可知，复杂互联电网的发电机电磁功率表达式为

式中:Pei为机组Gi的电磁功率，标幺值;E'i为机组Gi的电势，标幺值;δ为功角差，rad;G、B为雅克比矩阵中的参数;i，j为机组编号。

则机组G1的电磁功率表达式为

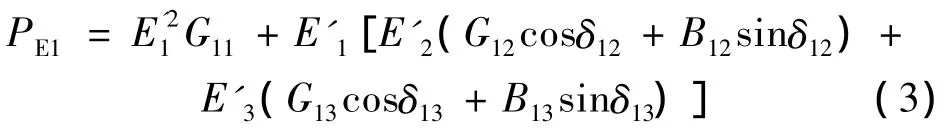
为分析方便对式(1)、(3)拆分和简化，将机组G1的电磁功率PE1看成分别供给通道L1－2和L1－3的电磁功率P12和P13之和，并忽略式中带电导Gij的项，得到式(4)、(5)为

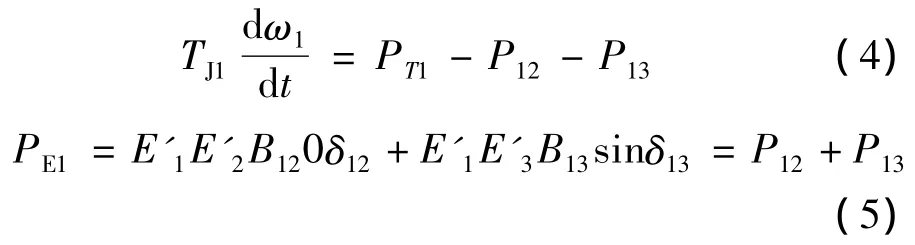
将式(5)中的P12和P13分别对时间t求导后，得到式(6)、(7)为

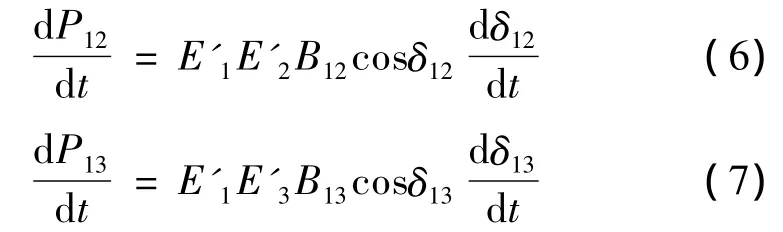
由于故障线路切除过晚或线路重载等因素，使得受扰动后的转子加速功率较大，减速阶段无法将其完全抵消掉。所以在第1失步周期内，失步通道两端的等效机组之间相对功角从一个很小的值逐渐增加到360°的过程，其值是呈“加速增加—减速增加—加速增加”的失步过程，显然，这期间始终是正值。

从式(6)和(7)可知，失步通道相对功角不断拉大的过程中和将先后由正值转为负值。即第1失步周期内，通道L1－2和L1－3的和参数总有一个在某一刻之后会满足的失步判据。

因此，故障后系统第1失步周期中，当最低电压点落入通道L1－2和L1－3之间的断面且最低点电压低于规定数值后，如果在相角差不断增加的过程中出现由负值转为正值，说明有发电机之间的功角差越过了不稳定平衡点，这时再有，则可以断定系统出现失步，满足所有判据的解列装置将动作解列相关通道，例如解列线路L1－2。

本文研究的重点是线路L1－2－1故障引起系统失步，解列通道L1－2后，通道L1－3上各判据参数的变化情况。

由于各通道线路参数、各自初始相对功角和其他辅助措施等因素的不同影响，即使是相邻通道的失步线路，其电磁功率变化也是有差别的，即:有可能出现在相邻通道都满足判据前提下，某通道提前满足功角变化率判据，从而先于其他通道解列的情况。

现假设机组G1与其他发电机之间功角差已越过了不稳定平衡点，即已由负值转为正值，通道L1－2和L1－3判据都已经满足，只等待判据满足后分别出口解列。

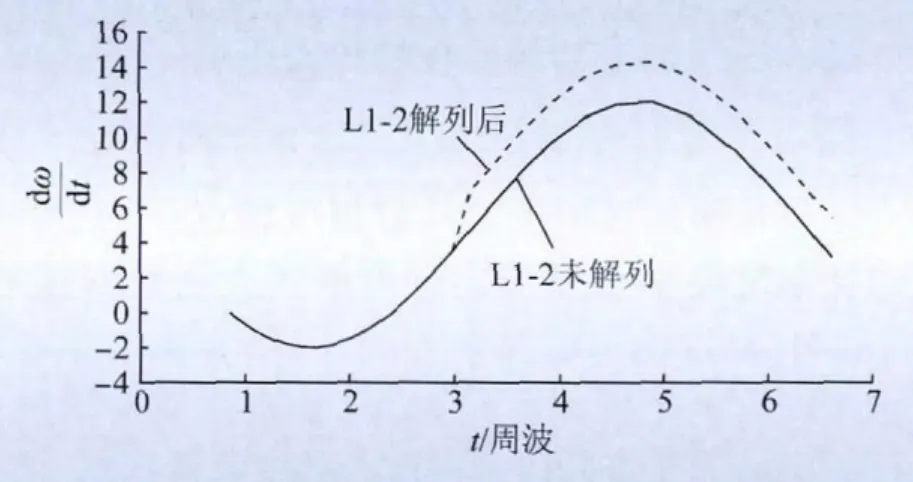
图2 判据对比图Fig.2 Criterion comparison

2.2 三机系统模型仿真验证

本文采用的三机算例，系统参数见表1～3，系统图如图1，使用BPA软件仿真。设置0.6 s时，双回联络线中的一条线路L1－2－1发生了三相短路故障，经过0.3 s后保护正确动作切除该联络线，由于潮流转移以及保护动作不及时，导致系统失步。通道L1－3所测快速解列相关判据变化情况如图3、4所示。计算结果验证了前面对多通道失步不同时解列时电气量特征推理的正确性和判据的有效性。

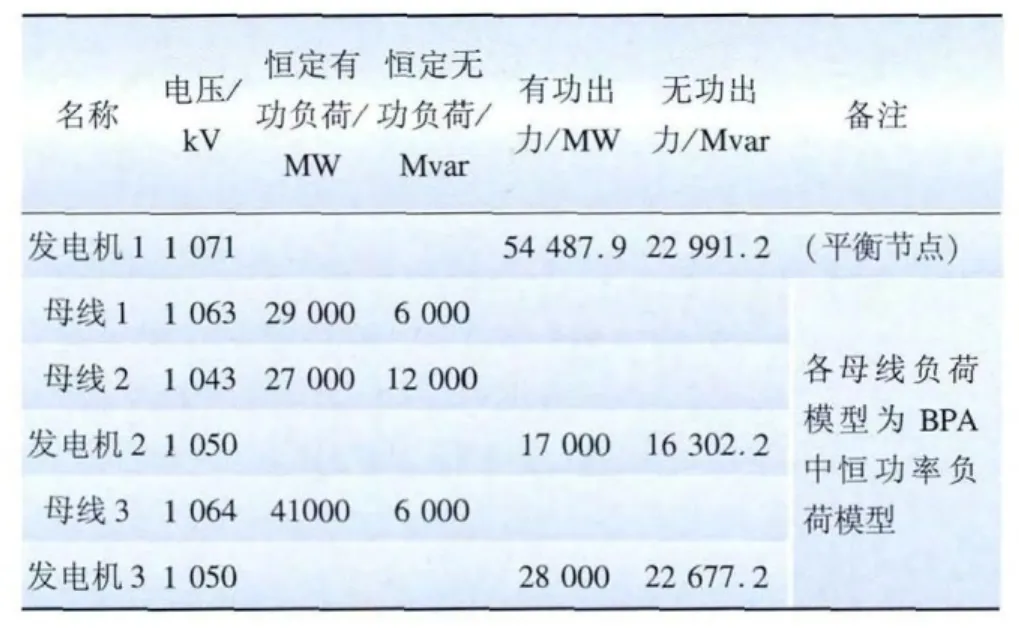
表1 三机算例节点参数Tab.1 Node parameters of three-machine model

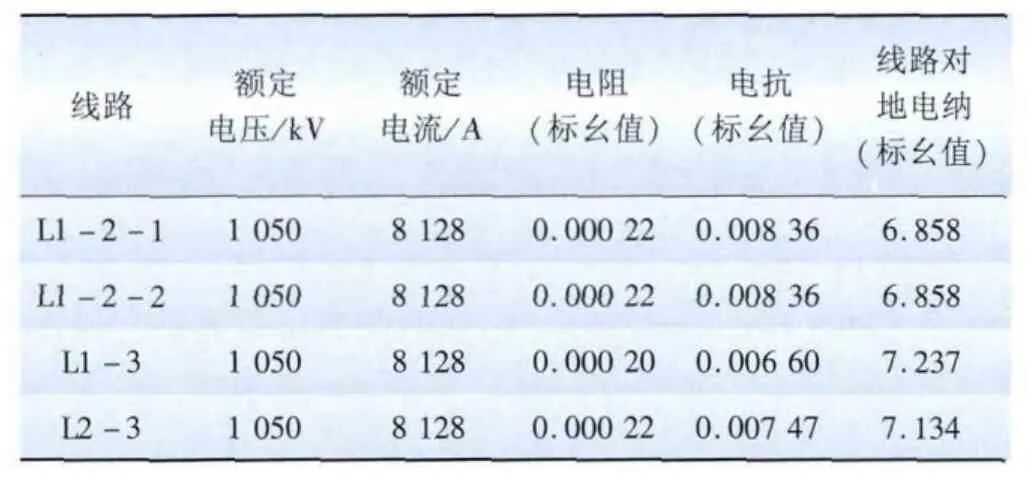
表2 三机算例线路参数Tab.4 Line parameters of three-machine model

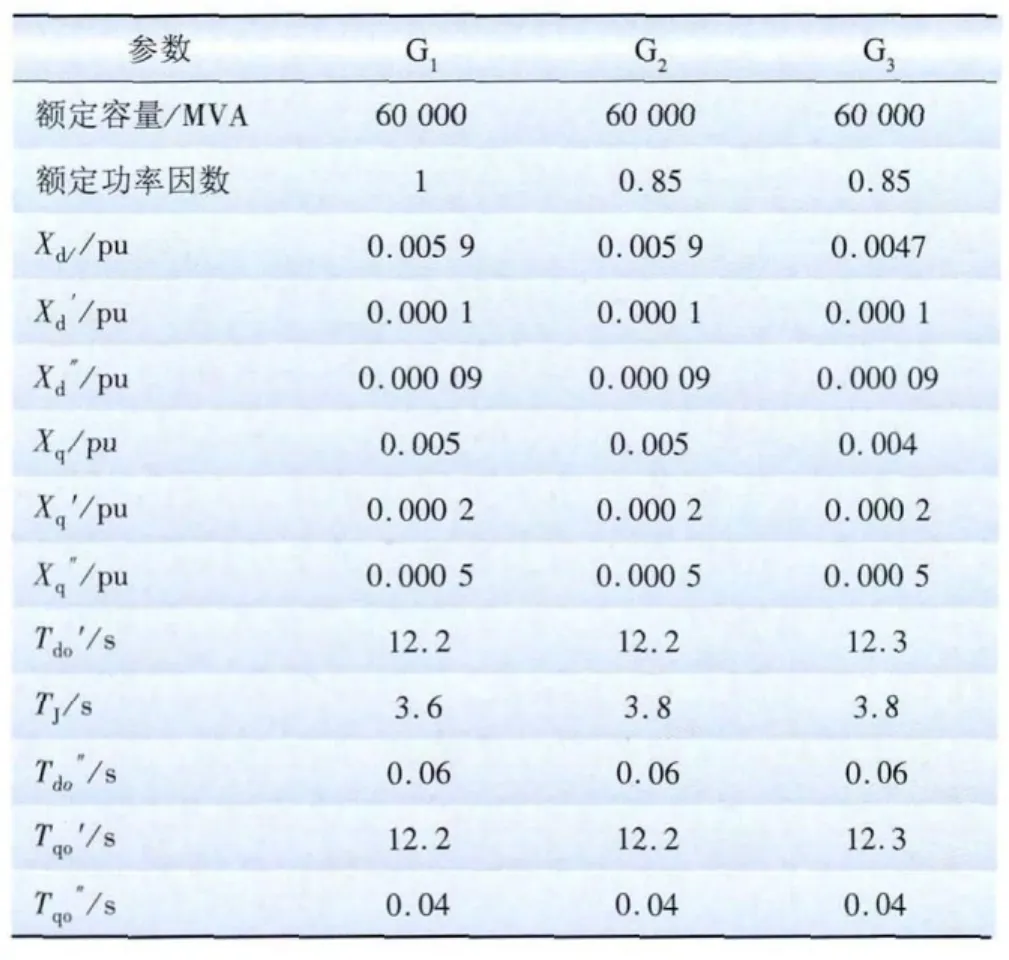
表3 三机算例发电机参数Tab.4 Generator parameters of three-machine model

图3 母线频率偏差Fig.3 Bus frequency deviation

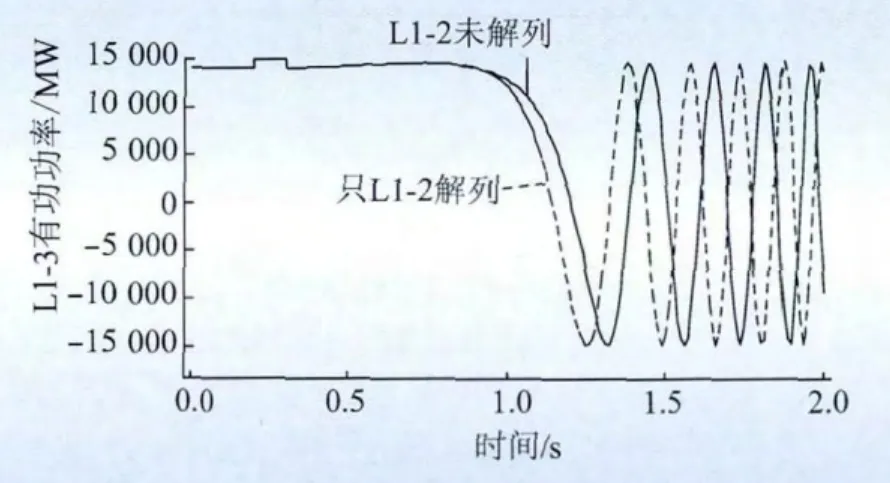
图4 线路有功功率Fig.4 Active power of line

图3、4说明2点:(1)不实施解列措施时，失步通道L1－3从0.84 s开始一段时间内满足快速解列判据，即通道两端相对功角明显持续拉大使;L1－3母线端频差经过故障加速减速后已过渡到再次加速增大阶段;有功功率判据也明显满足。(2)对比不实施解列措施时和解列掉联络线L1－2－2(图中简写为L1－2)后的联络线L1－3快速解列判据曲线，仿真结果与上面理论分析相吻合，相邻通道解列后剩余通道L1－3各结果值不仅满足判据要求，而且比相邻通道未解列时满足判据的时刻有所提前，判据值相对更快地满足判据要求。

上述理论推导和简单算例初步表明，在复杂多通道电力系统发生失步振荡时，快速解列判据可以在第1个失步振荡周期内识别出振荡中心所在线路，将不同步的2个系统正确及时分开，并且在不同时解列时先解列通道不会对后续解列的通道造成不良影响，反而加速后续通道的解列进程，以防止产生更恶劣的后果。

3 实际电网仿真验证

为了进一步验证快速解列判据于复杂多通道电力系统上应用的有效性，以中国2013年南方电网模型为算例，使用BPA软件仿真。设置0.2 s时，云南楚雄—广东穗东±800 kV直流双极闭锁故障，经过0.1 s切除楚穗直流两极节点并联无功负荷4 831 Mvar，由此导致系统失步。失步中心所在区域为广东—广西(两广)500 kV联络线路断面，此断面快速解列装置安装在连接两地区电网的各通道两端:桂林—贤令山双回失步通道、贺州—东坡双回失步通道、梧州—罗洞双回失步通道和茂名—蝶岭双回失步通道。图5为500 kV两广断面地理接线。

图5 500 kV广西—广东失步断面图Fig.5 500 kV Guangdong－Guangxi out-of-step section

在以下2种情况下仿真:(1)不设置快速解列措施，计算失步振荡时失步联络线断面两端功角差、有功功率变化规律以及振荡中心电压值;(2)在失步断面各通道上配置快速解列装置，研究快速解列判据在多通道复杂互联电网失步时是否能够将振荡线路在第1振荡周期内快速且正确解列，并验证第2节推理的不同时解列时加速判据满足结论的正确性。图6～8为茂名—蝶岭失步通道其中一回线快速解列各个判据变量仿真曲线图(由于各通道解列对振荡中心及振荡中心电压值并无直接影响，这里不再列出其仿真结果)。

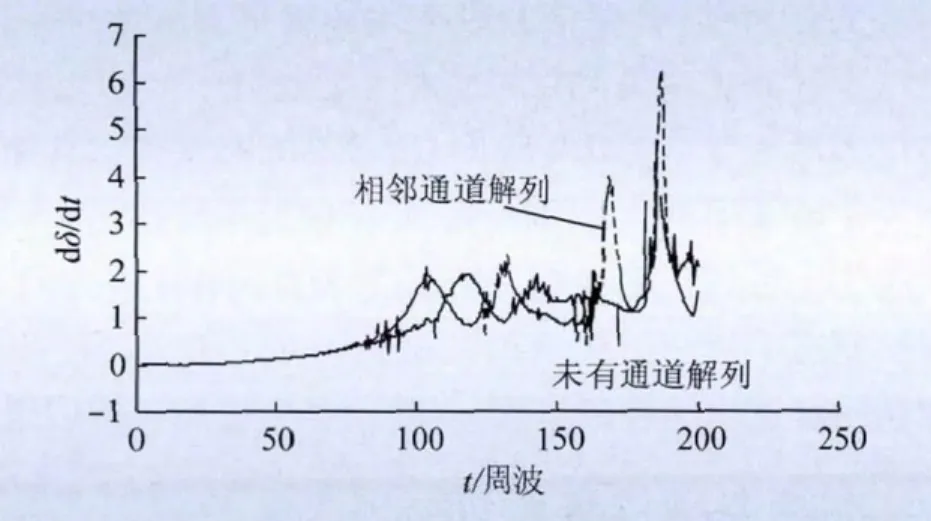
图6 茂名—蝶岭失步通道仿真结果图Fig.6 simulation result of Maoming-Dieling out-of-step channel

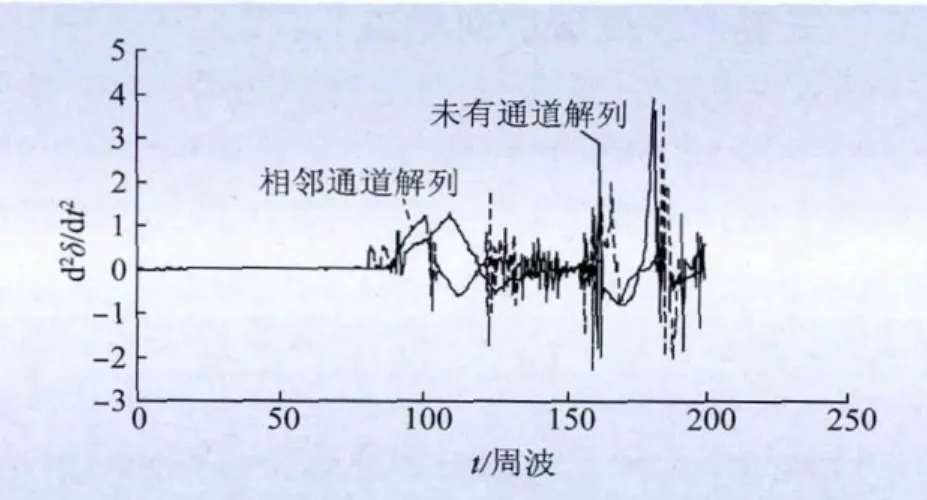
图7 茂名—蝶岭失步通道真结果图Fig.7 simulation result of Maoming-Dieling out-of-step channel

图8 茂名－蝶岭失步通道仿真结果图Fig.8 simulation result of Maoming-Dieling out-of-step channel

由图6～8实线曲线可知，110周波后该通道开始满足解列判据，即:同时满足而虚线曲线表明，其他通道的解列使得该通道在90周波后就满足快速解列判据了。

为使结论更清晰，提取图6～8中各个判据仿真值，得到两广失步断面中茂名—蝶岭双回线其中1回失步通道在其他失步通道不动作和已动作的仿真具体数值结果，如表4和表5所示。

结合图6～8实线曲线及表4和表5数据可以看出，茂名—蝶岭失步通道在其他通道未实施解列措施的情况下，于113～114.5周波满足功角变化率和频差变化率大于0、有功功率变化率值小于0;由图6～8虚线曲线可知，在其他失步通道满足快解判据将对应失步通道解列后，茂名—蝶岭失步通道达到解列条件的时间提前了22个周波，并且计算得到判据值也比其他通道不实施解列时显著，如其他通道实施快速解列措施后，此联络线有功功率变化率在91周波时已经达到了－2.93，而未实施解列措施的线路113周波时才达到了－2.65。

表4 茂名—蝶岭失步通道仿真结果(相邻通道未解列)Tab.4 Simulation result of Maoming－Dieling out-of-step channel(adjacent channel without splitting)

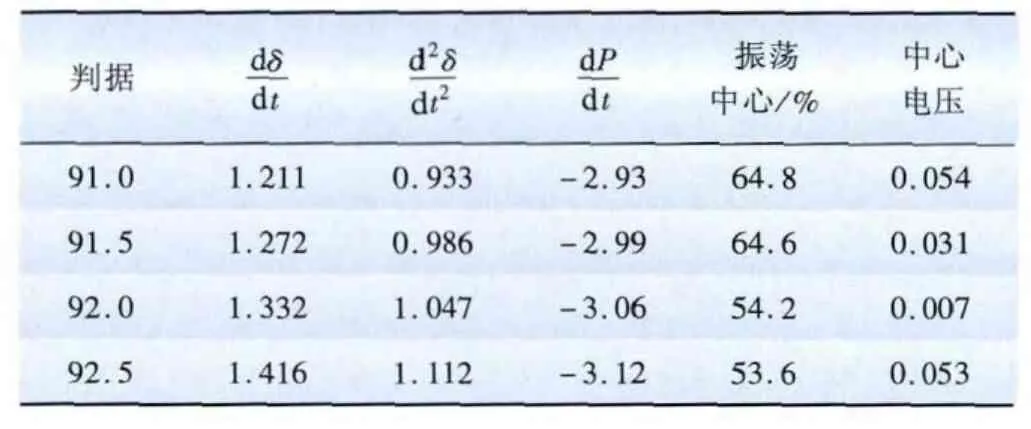
表5 茂名—蝶岭失步通道仿真结果(相邻通道解列)Tab.5 Simulation result of Maoming－Dieling out-of-step channel(adjacent channel splitting)

本例说明在多通道不同时解列时，以单通道设计的快速解列判据不仅是有效的，而且有加速剩余解列通道满足判据的功能，使得各个通道在第一失步周期内均能够快速解列，通道间解列并无不良影响，提高了解列后各个子系统的稳定性。由此表明，快速解列判据在复杂多通道电力系统应用是有效可行的，并且在解列速度上有其优越性。

4 结论

现有的快速解列判据是基于单机无穷大系统推导出来的，而对于复杂多通道互联电力系统，若要准确判断失步断面各个通道相继解列时是否相互干扰甚至引起拒动，仍需要从振荡机理进行理论分析和推导论证。

(1)根据多机系统发生失步振荡的机理推导分析，运用发电机转子运动方程和多机系统电磁功率公式，并对其做了合理的简化和拆分，得到快速解列功角变化率判据和有功功率变化率判据，可以在复杂多通道互联电力系统联络通道发生失步并且各通道不同时解列时应用的结论。

(2)理论证明出快速解列判据不仅可以判断复杂多通道电力系统失步通道，而且论证出这种解列方式能够在各通道不同时解列时，已解列通道的出口解列不会对后续解列通道满足判据造成不良的反向影响，而是加速后解列通道的解列进度。

(3)为验证本文推理的正确性，使用BPA仿真于三机系统模型和我国实际电网上，仿真结果证明了快速解列判据在复杂多通道电力系统不同时解列时具有优越性。

［1］高鹏，王建全，甘德强，等.电力系统失步解列综述［J］.电力系统自动化，2005，29(19):90-96.

［2］孙光辉，吴小辰，曾勇刚，等.电网第三道防线问题分析及失步解列解决方案构想［J］.南方电网技术，2008，2(3):7-11.

［3］潘贞存，桑在中，戴方涛，等.电网自动解列的新判据［J］.电力系统自动化，1995，19(7):34-37.

［4］蔡国伟，孟祥霞，李晓峰，等.基于网络结构及暂态能量的失步解列方案的研究［J］.中国电力，2006，39(12):7-10.

［5］孟祥侠，罗远翔，潘广林，等.合理配置输电网中STATCOM 对功角稳定的影响［J］.电力系统及其自动化学报，2011，23(2):69-75.

［6］Haner J M，Laughlin T D，Taylor C W.Experience with the R-Rdot Out-of-step Relay［J］.IEEE Trans.on Power Delivery，1986，1(2):35-39.

［7］汪成根，张保会，郝治国，等.一种电力系统失步解列面的实时搜索方法［J］.中国电机工程学报，2010，30(7):48-55.

［8］雷晓鹏.大型互联电力系统失步解列分析与研究［D］.陕西:西安理工大学，2008.

［9］王俊永，周敏，周春霞.快速失步解列装置在特高压电网的应用［J］.电网技术，2008，32(2):1-3.

［10］王永俊，许勇，汤涌，等.一种电力系统失步快速解列判断方法:中国，201010538013.6［P］，2010-11-10.

［11］王永俊，王慧铮，许勇，等.一种电力系统振荡中心快速定位方法:中国，200910087999.7［P］.2009-07-06.

［12］李光琦.电力系统暂态分析［M］.北京:中国电力出版社，2007.