覆冰状态下架空输电线路模型参数变化分析
刘根宁,呙 年,梁自超
(1.国网安徽省电力公司安庆供电公司,安徽省安庆市246003;2.上海电力学院电气工程学院,上海市200090)
0 引 言
覆冰对于电力系统来说,是一种严重的自然灾害,严重威胁电力系统的安全稳定运行。我国地域广阔,地形复杂,气候多变,面临的覆冰危害相当严重。导线覆冰导致的电力系统事故,严重威胁电力事业的发展,影响正常的国民经济生活。
近年来,国内外不断出现电力系统遭受冰雪灾害的事故。文献[1]介绍了美国和加拿大的电网近年来遭受的大范围、长时间的冰冻灾害。文献[2]对我国各类输电线路发生的冰害事故做了详细统计。文献[3]介绍了2008年初,我国南方遭受的有气象记录以来的最严重的冰雪灾害天气,在此次冰雪灾害天气中,湖南、江西、贵州、浙江等地区的电网受灾十分严重,出现了大范围的冰闪跳闸和断线倒杆,导致大面积停电和部分电网解裂等事故。为了保证电网系统安全可靠运行,国家电网公司对输电线防雪灾、冰灾提出了更高的要求,因此,对输电架空线路覆冰进行深入的研究具有十分重要的实际应用价值。
输电线路覆冰作为一项世界性难题,国外研究起步较早,国内在2008年初的冰灾发生后,才对线路覆冰进行了大量的研究工作。文献[4]介绍了覆冰对电力系统造成的各种危害。文献[5]分析了我国输电线路因覆冰而导致事故频发的主要原因。文献[6]介绍了目前常用的输电线路的除冰防冰措施。
国内外科研人员对覆冰架空线路已经做了大量研究工作[7-15],主要集中在导线覆冰的机理、不同覆冰模型的分析对比以及覆冰导线的舞动和输电线路的防冰、除冰技术等方面。目前,关于架空输电线路的数学模型的理论已经比较成熟,然而这些理论中的线路模型很少考虑线路覆冰后的情况,但是架空输电线路在覆冰状态下,线路模型中的参数将会发生变化。因此,本文通过分析架空输电导线周围的电场和磁场分布,并经过电磁场的相关计算,研究覆冰状态下架空输电线路模型中相关参数的修正问题。
1 覆冰状态下架空输电线路模型参数的修正
1.1 覆冰状态下架空线路电阻的变化
有色金属导线每相单位长度的直流电阻可按下式计算:

式中:R 为导线每相单位长度的直流电阻,Ω/km;ρ为导线的电阻率,Ω·mm2/km;S 为导线载流部分的标称截面积,mm2。
按公式(1)计算所得的电阻值,都是指温度为20 ℃时的值,在精度要求较高时,温度t 时的电阻值Rt可按下式计算:
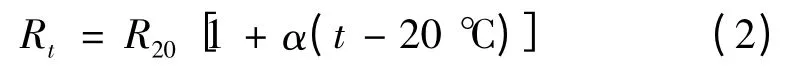
式中:Rt、R20分别为t、20 ℃时的电阻;α 代表电阻温度系数[16]。
对于覆冰状态下的架空输电线路,由于导线外层所覆盖的冰层基本不导电,可以认为输电导线载流部分的截面积S 保持不变;此时,电力线路的电阻率仅与载流部分的材料有关,所以架空输电线路在覆冰状态下电阻率ρ 保持不变。覆冰状态下,影响架空输电线路电阻的因素为线路实际运行的温度。
架空线路覆冰时,其实际运行温度与没有覆冰时差别不大,因此,覆冰状态下架空线路的电阻与不覆冰的架空线路相差不大。
1.2 覆冰状态下架空线路电抗的变化
通过对三相线路导线周围磁场的分析,经过相关计算可以得出计及三相架空线路换位后,导线单位长度的电抗表达式:
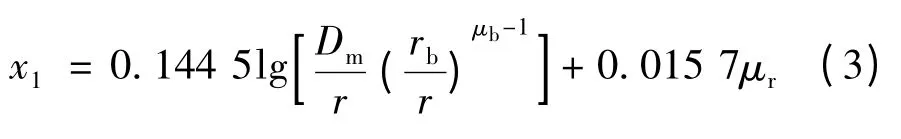
式中:x1为导线单位长度的电抗,Ω/km;r 是导线的半径,cm 或mm;rb是冰层的厚度与导线半径之和,cm 或mm;μb是冰的相对导磁系数;Dm代表几何均距,cm 或mm;μr为导磁系数。
由式(3)可知,线路的电抗实际上有2个部分组成。第1 部分如式(4)所示,其取决于导线的布置方式和截面积,但与是否导磁无关。这部分是由导线的外部磁场所决定的,因此称为导线的外电抗。覆冰状态下的架空线路由于在导线外部所覆盖的冰层会对导线的外部磁场产生影响,因此,覆冰状态下架空线路电抗的修正需要对导线的外电抗进行修正。
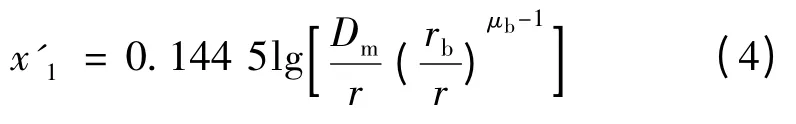
第2 部分如式(5)所示,其只与导磁系数μr有关,从而取决于导线的导磁。这部分是由导线的内部磁场所决定的,因此称为导线的内电抗。导线覆冰后并不会对导线的内部磁场产生影响,即导线的内电抗不变。因此,覆冰状态下架空线路电抗的修正只需要对导线的外电抗进行修正。
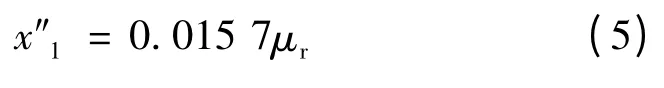
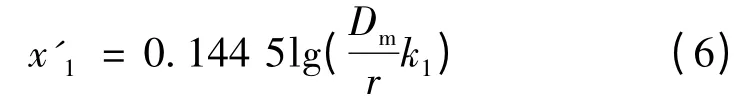
由于冰的相对导磁率μb≈1,即k1≈1,所以
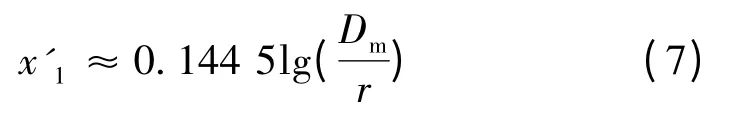
因此覆冰后架空线路的电抗与非覆冰时架空线路的电抗相差不大,覆冰对架空线路电抗的影响可以忽略不计。
1.3 覆冰状态下架空线路电导的变化
线路的电导取决于沿绝缘子串的泄漏和电晕。线路的电导可采用下式计算:
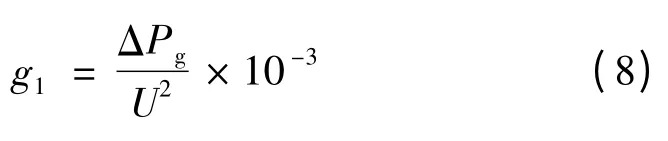
式中:g1为导线单位长度的电导,S/km;ΔPg为三相线路泄漏和电晕损耗功率,kW/km;U 为线路电压,kV。
覆冰状态下,架空输电线路电导的变化与当时的气象情况和空气的相对密度有关。当在天气较恶劣,空气湿度较大时,临界电压会有所降低,这就会增加发生电晕的可能性或增大电晕损耗,而输电线路的电导与电晕损耗成正比,有可能使线路的电导增大。
但是实际上,由于沿绝缘子串的泄漏通常很小,而在设计线路时,就已经检验了所选导线半径能否满足在晴朗的天气下不发生电晕的要求,一般情况下,可以认为g1≈0。
1.4 覆冰状态下架空线路电纳的修正
1.4.1 单相架空线路的电纳
线路的电纳取决于导线周围电场的分布,2 点之间的电位差及单相线路周围的电场示意图如图1、2所示。单根导线单位长度电荷为q 时,距导线中心x处的电场强度Ex为

式中:εr为相对介电常数(对空气,εr=1;冰的相对介电常数为εb)。
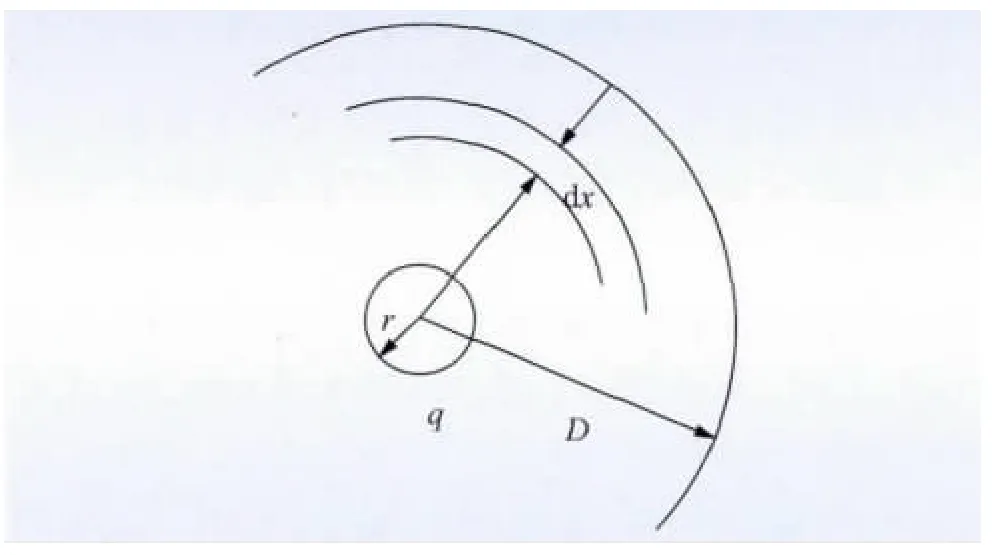
图1 2 点之间的电位差Fig.1 Potential difference between two points
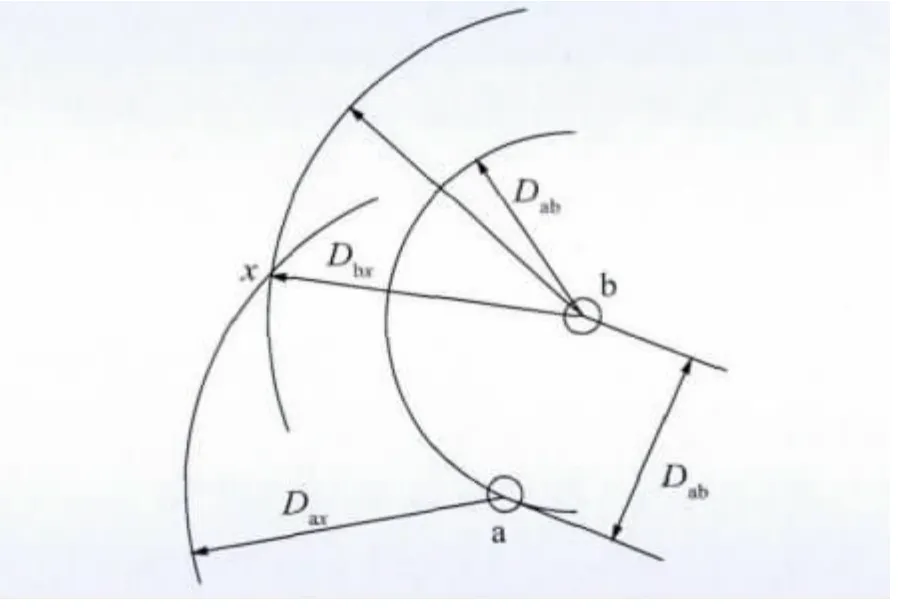
图2 单相线路的电场Fig.2 Electric field of single-phase wire
图1 中导线表面与距导线表面D(D >rb)处某一点之间的电位差urD为
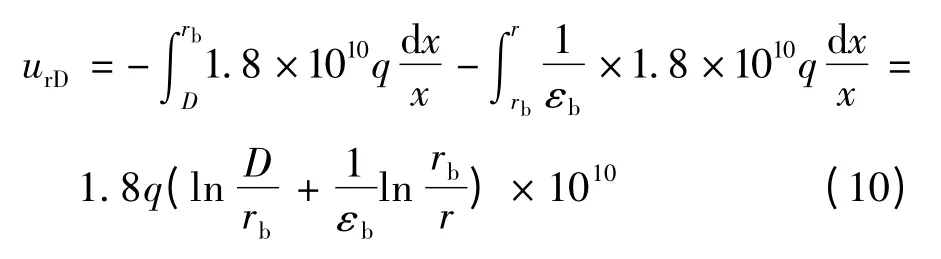
用叠加原理分析可得a 线(或b 线)对中点的电容为
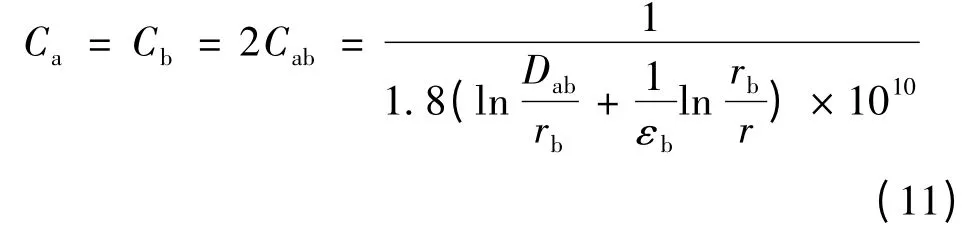
经换算可得电纳b1的表达式如下:
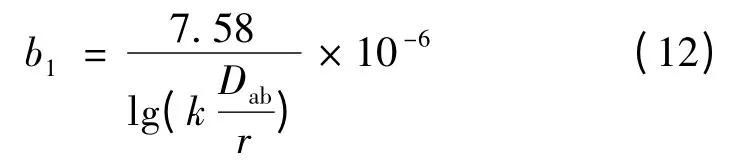
其中修正系数k2为
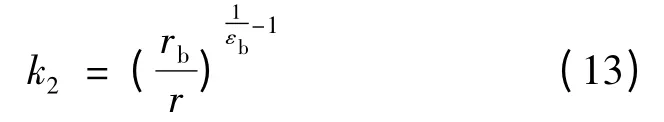
由式(12)可知,单相架空线路覆冰后会使线路的单位电纳增大,且单位电纳的增量与导线外部的覆冰厚度成正比。
1.4.2 三相架空线路的电纳
通过对三相线路导线周围电场的分析和相关计算,可以得出计及三相架空线路换位后,覆冰状态下单位长度架空线路电纳的计算式为
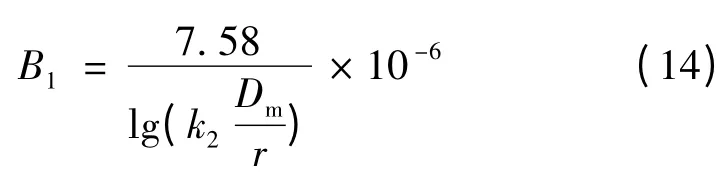
由式(14)可知,三相架空线路的单位电纳与导线的半径和导线外层覆冰的厚度以及导线的几何均距Dm有关。取冰层的相对介电常数εb为80,当架空线路覆冰的厚度取不同值时,LGJ-185/10、LGJ-300/50、LGJ-400/50、LGJ-500/45、LGJ-630/45 这5 种导线单位电抗的数值变化见表1。其中,设d 为导线覆冰的标准厚度,d=0 表示导线没有覆冰的情况,且各导线均为水平排列,2 相导线之间的距离分别为5、8 和13 m。
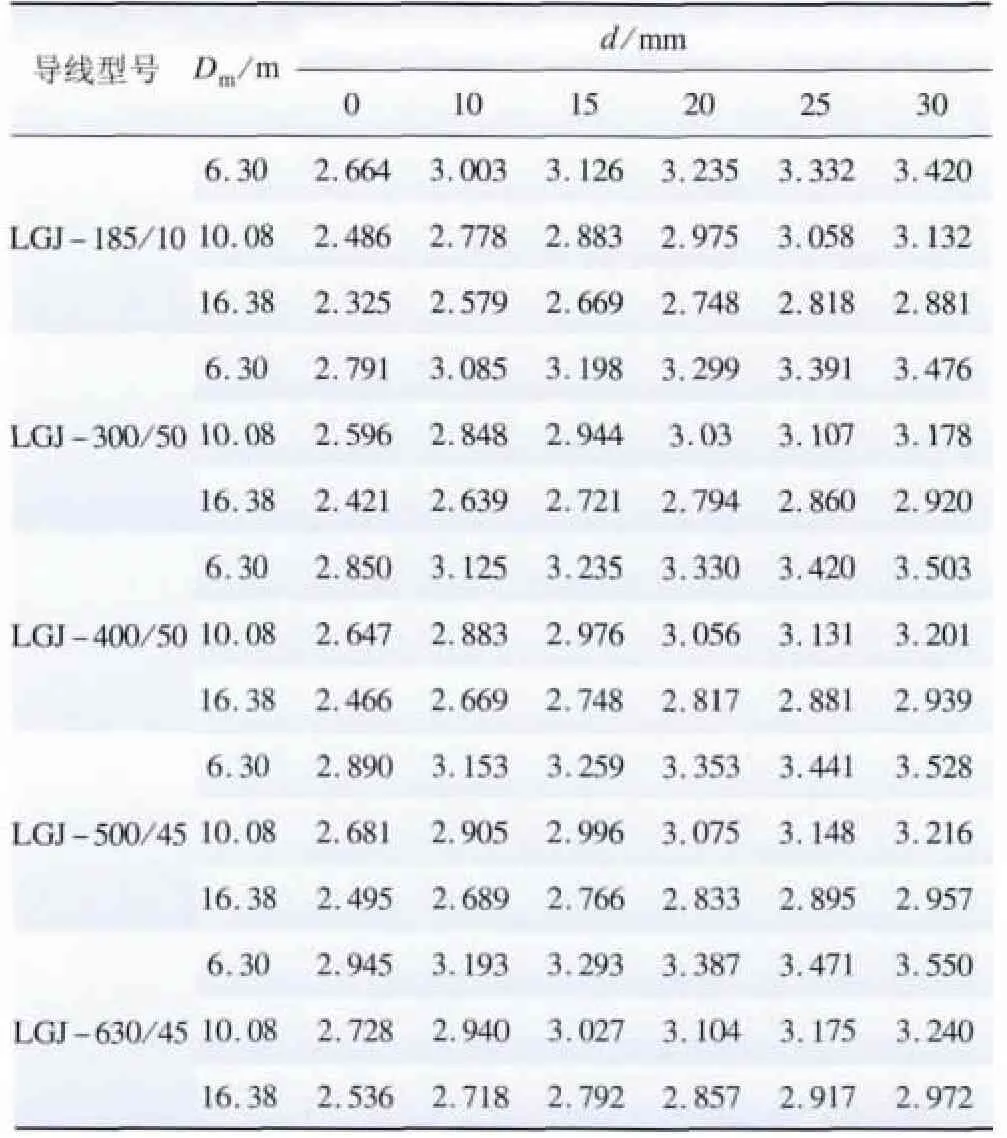
表1 不同覆冰厚度下三相架空线路的电纳Table 1 Susceptance of three-phase overhead lines under different ice thickness 106S/km
图3 为LGJ-400/50 导线在不同覆冰厚度和几何均距下单位电纳的变化曲面,当几何均距为10 m 时,导线单位电纳与覆冰厚度和导线半径的关系曲面如图4 所示。
由图3、4 可知,同种导线,几何均距越小,覆冰后导线的电纳越大;当几何均距一定时,导线半径越大,覆冰后线路电纳越大。图5 为根据图4 所得的截面图,即在导线几何均距为10 m 时,5 种不同导线的三相单位电纳值随导线覆冰厚度的变化趋势。由图5 可知,三相架空线路覆冰后会使线路的单位电纳增大,且单位电纳的增量与导线外部的覆冰厚度成正比。
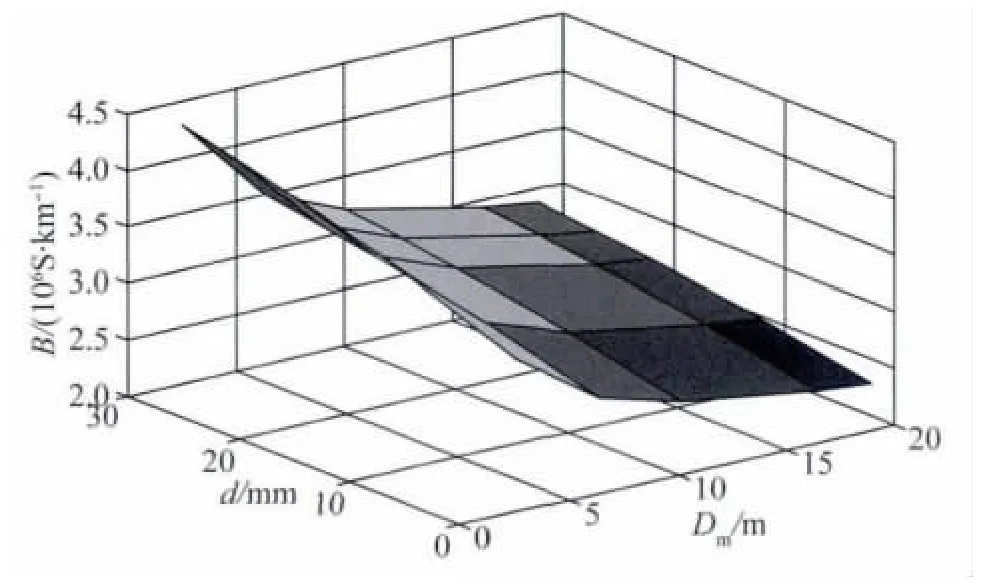
图3 单位电纳与覆冰厚度和几何均距的关系曲面Fig.3 Curved surface of unit susceptance,ice thickness and geometric mean distance
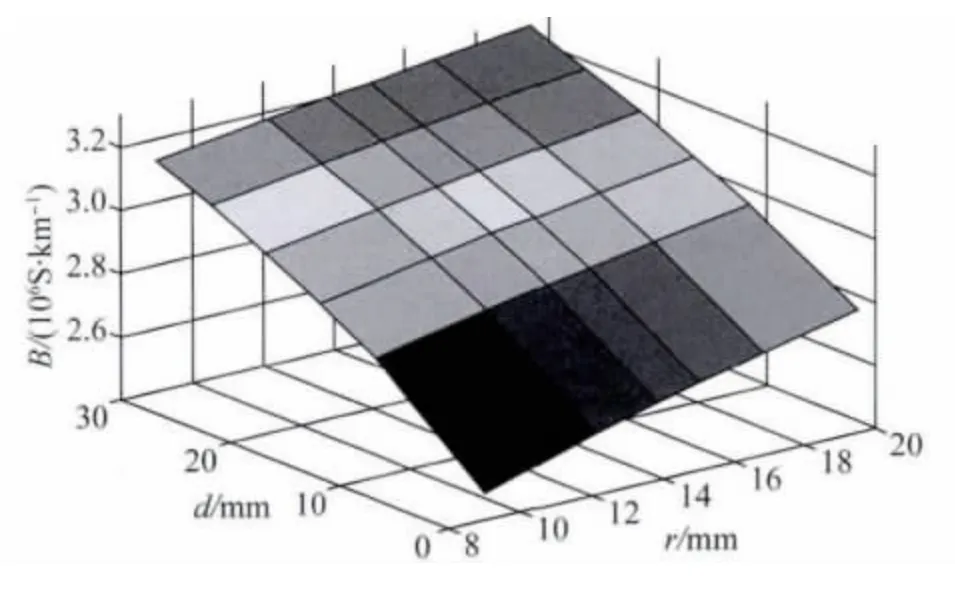
图4 单位电纳与覆冰厚度和导线半径的关系曲面Fig.4 Curved surface of unit susceptance,ice thickness and wire radius
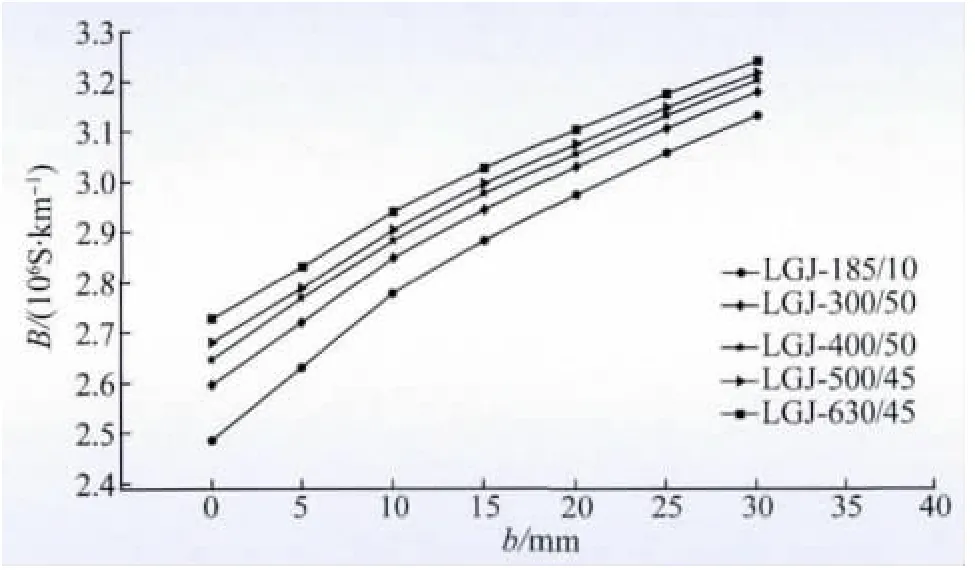
图5 不同导线单位电纳与覆冰厚度的关系图Fig.5 Relationship between unit susceptance of different wires and ice thickness
从表1 中可以看出,各种类型的导线在不同覆冰厚度和不同分裂间距下线路的单位电纳值。但是,覆冰后线路电纳相对没有覆冰时电纳变化的百分数可以更加直观地显示出电纳变化的规律。不同覆冰厚度下三相架空线路电纳变化的百分数ΔB%如表2 所示,ΔB 的定义如式(15)所示:
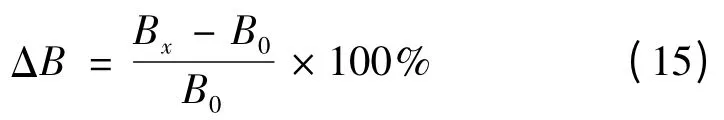
式中B0、Bx分别表示导线在覆冰前后的单位电纳值。
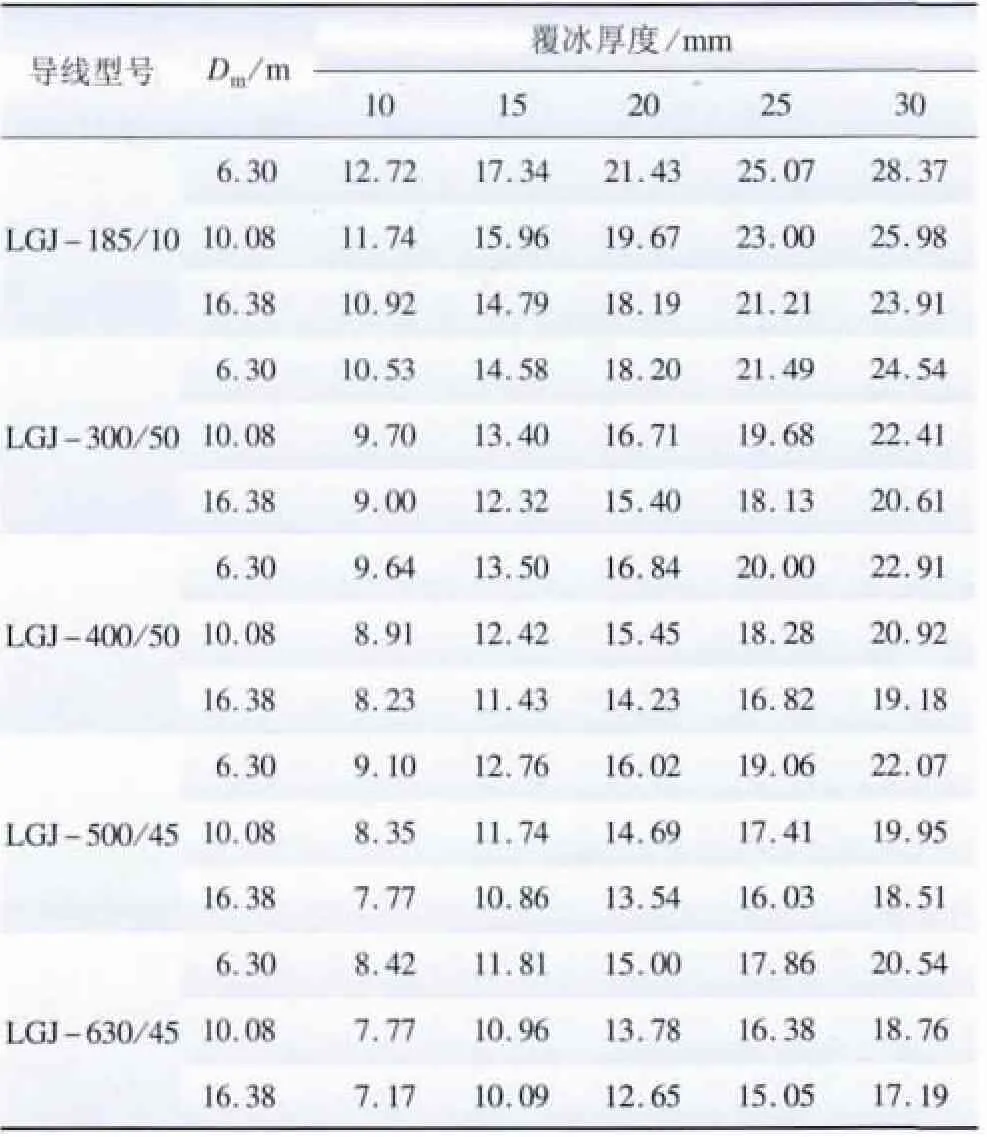
表2 不同覆冰厚度下线路电纳变化量的百分数ΔB%Table 2 Percentage of susceptance variation ΔB% of lines under different ice thickness %
由表2 可知,在相同条件下,导线几何均距越小,导线覆冰后电纳变化越大;在相同条件下,导线半径越小,导线覆冰后电纳变化越大;在相同条件下,覆冰厚度越大,导线覆冰后的电纳变化越大。
在工程计算中,当覆冰线路电纳的变化量小于10%时,可以忽略覆冰对电纳的影响。由表2 可知,当覆冰厚度为10 mm(轻度覆冰)时,线路覆冰对电纳的影响较小,大多数数据可以忽略。当线路覆冰厚度为30 mm(重度覆冰)时,线路覆冰对电纳的影响很大,电纳的变化量在20%左右,此时必须考虑覆冰对线路电纳的影响。
2 覆冰状态下架空线路的数学模型
在电力系统的稳态分析中电力线路的数学模型就是以电阻、电抗、电导、电纳表示的它们的等值电路。按式(1)、(3)、(8)、(14)求得单位长度的电阻、电抗、电导、电纳后,就可以作出最原始的覆冰状态下架空电力线路等值电路,如图6 所示。
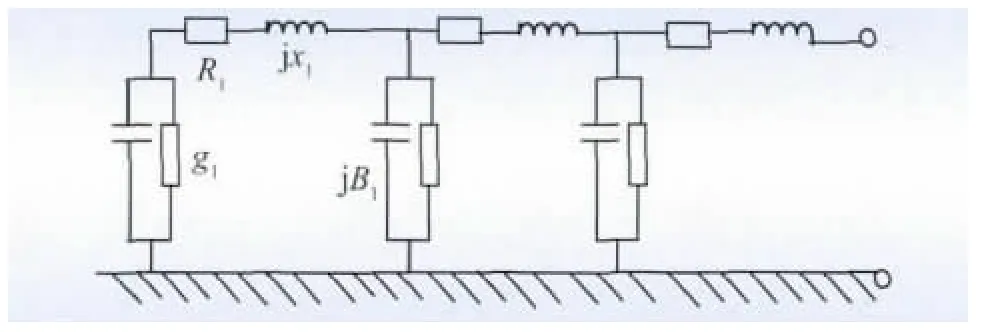
图6 电力线路的单相等值电路Fig.6 Single-phase equivalent circuit of transmission line
3 结 论
覆冰对架空输电线路参数的影响,主要体现在对电纳的影响上,覆冰对电阻、电抗、电导的影响很小,基本可以忽略。导线覆冰会使线路的单位电纳明显增大,为得到更加精确的线路模型,在对中等及中等以下长度的架空输电线路建立数学模型时,也应当考虑分布参数特性的影响。本文论述的覆冰修正模型能为输电线路设计单位提供参考,具有一定的实际应用意义。
[1]Fu P.Modelling and simulation of the ice accretion process on fixed or rotating cylindrical objects by the boundary element method[D].Canada:Université du Québec,2004.
[2]孙才新.重视和加强防止复杂气候环境及输变电设备故障导致电网大面积事故的安全技术研究[J].中国电力,2004,37(6):1-8.
[3]周卫华,蒋兴良.输电线路绝缘子冰闪防治措施的研究[J]. 湖南电力,2008,28(1):1-5.
[4]蒋兴良,易辉.输电线路覆冰及防护[M].北京:中国电力出版社,2002:6-11.
[5]陈凌.旋转圆柱体覆冰增长模型与线路覆冰参数预测方法研究[D].重庆:重庆大学,2011.
[6]周迪,黄素逸.覆冰导线风动脱冰研究[J].长沙电力学院学报:自然科学版,2002,17(2):54-56.
[7]蒋兴良,周仿荣,王少华,等. 输电导线覆冰舞动机理及防治措施[J].电力建设,2008,29(9):14-18.
[8]李成榕,吕玉珍,崔翔,等.冰雪灾害条件下我国电网安全运行面临的问题[J].电网技术,2008,32(4):14-22.
[9]张欢,李炜,张亚军,等.输电线路档距组合对覆冰导线动态特性的影响分析[J].高电压技术,2013,39(3):755-761.
[10]景乾明,胡春梅,胡基才,等.微地形对输电线路舞动的影响[J].电力建设,2012,33(6):23-26.
[11]Fan R X,Wu S N. A new type of DC de-icing system for transmission lines a power-electronics-based transmission line deicing system[C]// International Conference on Electrical and Control Engineering (ICECE),Wuhan,China:IEEE,2010:4916-4919.
[12]李海若,郭海超,谢强. 薄覆冰导线气动力特性风洞试验研究[J].电力建设,2013,34(3):12-16.
[13]Q/GDW 179—2008 110 ~750 kV 架空输电线路设计技术规定[S].北京:国家电网公司科技部,2008.
[14]陆航波.2008年桂北架空线路覆冰的初步分析[J]. 红水河,2009,28(2):98-101.
[15]舒立春,王晓峰,蒋兴良.输电线路冰区划分方法分析[J]. 电力建设,2009,30(1):44-46.
[16]陈珩.电力系统稳态分析[M]. 北京:中国电力出版社,2007:30-30.

