混合储能系统中超级电容的作用及容量设计方法

黄秀琼，丁若星，肖 曦，王 奎，田培根

(1．广西电网公司，南宁市530023;2．中国舰船研究设计中心，武汉市430064;3．电力系统及大型发电设备安全控制国家重点实验室(清华大学电机系)，北京市100084)

0 引 言

储能系统是微电网不可或缺的组成部分，能起到紧急供电、调峰、提升电能质量等作用［1］。超级电容具有功率密度大、循环寿命长、效率高、大电流充放电不影响寿命等优点，但是能量密度小。因此，将能量密度大的锂离子电池与功率密度大的超级电容组成混合储能系统(hybrid energy storage system，HESS)，可以使储能系统兼备较好的功率特性和能量特性［2］。

文献［3］分析比较了混合电源系统中超级电容与蓄电池直接并联、通过电感器并联、通过功率变换器并联这3 种结构的性能，但储能形式和控制的灵活性有限。为获得更充分的控制灵活性，更好地实现控制目标，可以对不同类型的储能装置进行独立控制;将不同类型储能装置分别经双向DC/DC 变换器升压后并联，是一种普遍采用的拓扑［4］。通过控制对应DC/DC 变换器，可实现对不同类型储能装置的功率调节。

以交流母线型微电网中超级电容和锂离子电池组成的混合储能系统为例，直流母线通过双向DC/AC 变换器接入微电网，来实现储能系统与微电网的功率交换。直流或交直流混合母线型微电网中，光伏、风力发电机等微电源以及负荷可以并联到直流母线上，直接与储能系统进行功率交换。

根据超级电容与锂离子电池的功率和能量特性，基于频率分解的滤波法作为混合储能系统功率分配的方法被广泛采用，即利用滤波器将波动的储能系统整体功率指令分解为高频分量和低频分量，然后将其分别分配给功率特性较好的超级电容和容量较大的电池［5-7］。为提高混合储能的经济性，文献［8］给出一种基于遗传算法的超级电容器蓄电池混合储能系统的容量设计方法，但算法相对较复杂，且主要只针对经济成本目标进行优化。

本文针对锂离子电池和超级电容经Buck-Boost双向DC/DC 变换器升压后共用直流母线的混合储能系统，详细分析其电流响应特性;根据超级电容在储能系统中应起到的作用，给出一种基于荷电状态的功率分配方法，以及在此功率分配方法下超级电容基于需求的容量设计依据，并结合直驱型波浪发电输出功率的波动特性给出算例。尽管在混合储能系统实际应用中应同时对超级电容和电池容量进行设计，但锂离子电池的容量设计方法不在本文的讨论范围内。

1 混合储能系统电流响应特性分析

图1 为交流母线型微电网中超级电容和锂离子电池组成的混合储能系统。图中的双向DC/DC 变换器可采用如图2 所示的拓扑结构，其中ui为输入端电压，uo为输出端电压。这种拓扑结构简单，通过控制电感电流iL平均值的大小和方向，即可实现功率的双向流动。超级电容或电池接入输入端后，可将uo或iL作为控制目标，通过改变桥臂上下管开通的占空比来实现控制。

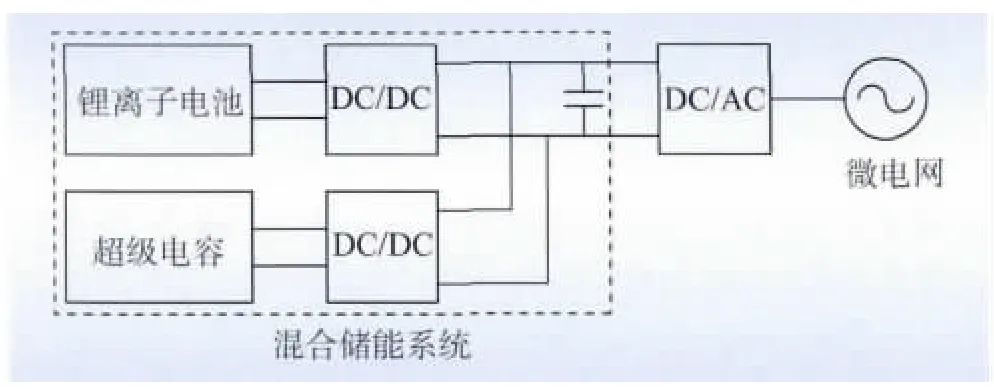
图1 交流母线型微电网中混合储能系统结构示意图Fig.1 HESS structure in microgrid with AC bus

图2 双向DC/DC 变换器拓扑Fig.2 Topology of bidirectional DC/DCconverter

设开关周期为T，电感值为L，桥臂下管导通的占空比为D;iL参考方向如图2 所示，且有uo＞ui。电流连续模式下的方程如式(1)所示。由式(1)可知，电流瞬时值变化率仅由ui、uo和L 决定。

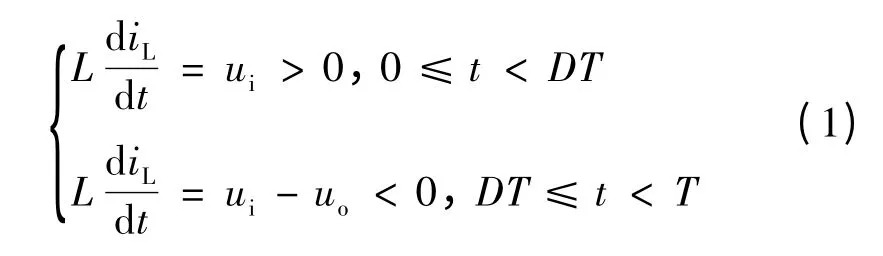
当下管占空比为D 时，经过1个周期，电流平均值的增量ΔI 为

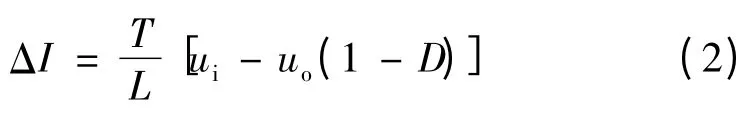
若D 的上限设为Dmax，则电感电流平均值的最大变化率为

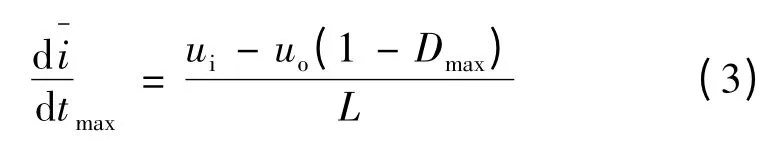
由式(1)和(3)可知，电感电流平均值的最大变化率始终小于电感电流瞬时值的最大变化率。

下面给出图2 所示DC/DC 变换器电流响应的仿真结果。假设ui= 50 V，uo= 100 V，T = 0.1 ms，L = 5 mH，Dmax= 0.9;电流指令从－10 A 阶跃至10 A。根据式(2)可算得1个周期内电流平均值的最大增量为0.8 A;若占空比能始终保持最大值0.9，则电流实际值跟上电流指令值需要经过25个周期，即2.5 ms。

使用上述参数和图3 所示的电流控制策略，在Matlab/Simulink 环境下进行仿真;电流实际值iL对电流指令值iLref的跟踪情况如图4 所示。电感电流指令值发生阶跃后，实际电流平均值经过约2.5 ms 跟上指令值;电流平均值变化率受瞬时值变化率的限制，并与电流环PI 调节器参数有关。

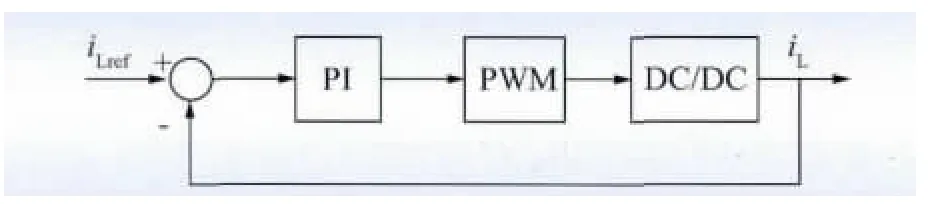
图3 电流控制框图Fig.3 Block diagram of current control

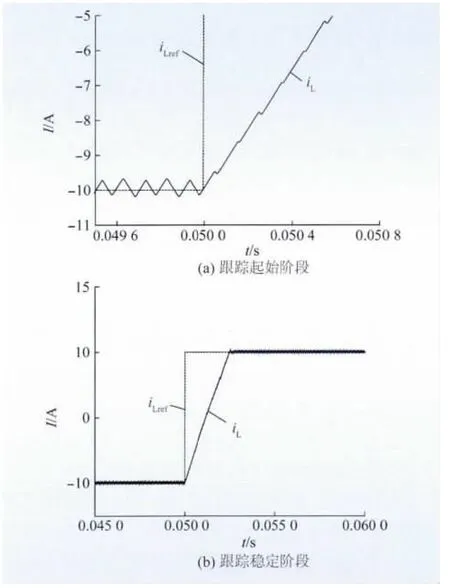
图4 DC/DC 变换器电感电流对指令值的跟踪Fig.4 Inductor current of DC/DCconverter tracking on command value

在如图1 所示，储能装置经DC/DC 变换器升压后并联的结构下，由文献［9-11］可知，电池和超级电容均可采用不含电感元件的模型，可将储能装置等效成端电压随荷电状态和电流变化的电压源，而不必考虑其本身对电流响应速度的影响。

由前文分析可知，DC/DC 变换器电感电流平均值的最大变化率受输入输出端电压、占空比上限和电感值影响。其中，电感值的选取与抑制电流纹波的要求相关;电感值越大，电流纹波越小。与电池相比，超级电容对充放电电流大小的限制较少，能够承受更大的电流纹波;因此，在必要时，超级电容可以通过减小对应DC/DC 变换器的输入电感，达到比锂离子电池更快的电流响应速度。

2 超级电容的作用

文献［12］给出了超级电容储能电站和锂离子电池储能电站相关参数的对比，其中，超级电容的能量单价是锂离子电池的30 倍。由于成本的限制，在混合储能系统的实际应用中，超级电容的储存能量一般比锂离子电池小得多，难以进行长时间的功率支撑。

虽然超级电容的能量密度小，但其功率密度大、循环寿命长、可进行大电流快速充放电的优点是锂离子电池不具备的。充放电倍率过大将严重影响电池寿命［13-14］。根据文献［13］的实验结果，与1C 的充电倍率相比，单体电池在1.1C 和2C 充电倍率下的循环寿命衰减分别加快了约15%和40%。

混合储能系统的设计初衷是发挥不同类型储能装置的优势，以获得较好的综合性能。根据前文给出的超级电容与锂离子电池特性的对比分析，可利用功率特性较好的超级电容响应储能系统整体的短时大功率指令，而利用更易达到大容量规模的电池满足对储能系统较长时间尺度内的能量需求。超级电容响应尖峰功率，可避免锂离子电池短时间内的高倍率充放电和深度放电。而在某些合适的功率指令波动情况下，如能充分利用超级电容的容量，尽量减小锂离子电池的充放电循环次数，也可在一定程度上延长锂离子电池的使用时间。

荷电状态(state of charge，SOC)反映电流的累积效应，变化较电流和功率缓慢;采用式(4)所示的功率分配方法，使电池的功率指令随超级电容SOC 平缓地变化，则能够利用超级电容的容量平抑电池功率的波动，使超级电容得以发挥上述2 点作用。

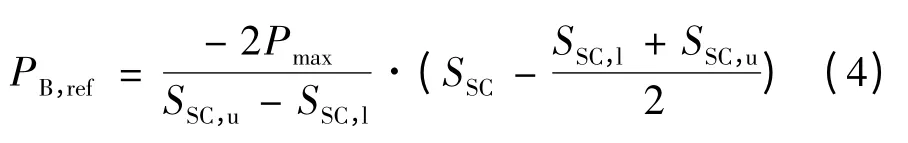
式中:Pmax为混合储能系统整体功率指令绝对值的上限;PB，ref表示电池的功率指令;SSC为超级电容SOC;SSC，u和SSC，l分别为SSC的上限和下限。

功率以储能装置放电为正，根据式(4)得到电池的功率指令后，超级电容功率指令由直流母线电压环的输出得到。PB，ref与SSC成线性关系，SSC过高则电池充电，从而迫使超级电容放电;反之亦然。

对于额定端电压U 和容值C 一定的超级电容，其额定储存能量W = CU2/2 一定。由于超级电容的储存能量与锂离子电池相比十分有限，所以针对发电功率与负荷之间的功率差额，超级电容一般用于将某段时间内的功率波动平抑成该段时间内的功率平均值，而由锂离子电池处理这段时间内平均功率与实际所需功率之间的差值。

采用第2 节所述的功率分配方法时，由于不再以常规滤波法采用的频率作为功率分配依据，所以不需对功率波动进行分解，可以直接根据需平抑的功率波动波形来设计超级电容容量。

下面分析额定储存能量W 一定的，超级电容能处理的，平均值为0 的周期性波动功率，其最大幅值与波动频率的关系。以正弦波为例，对角频率ω =2πf、幅值为Pm的正弦波来说，令功率波形正半周对时间的积分不超过W，即

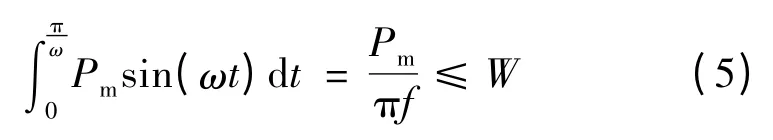
则允许的功率波动最大幅值Pm，max= πWf，与频率f 成正比。

将规则的功率波形推广到任意功率波形P(t)。若利用超级电容将一段时间内的功率波动P(t)平抑成该段时间内的平均功率Pavg，则需要超级电容储存或释放的最大能量为

式中t1、t2分别为该段时间内P(t)－Pavg与时间轴包围面积最大部分的起止时间。

下面以平抑波浪发电输出功率的波动为例，定性分析超级电容容量的设计原则。

直驱型波浪发电装置输出功率的波动分为长时间尺度和短时间尺度二种形式。其中，长时间尺度的功率波动与风力发电和光伏发电一样，指在数10 min 或h 级的时间尺度上，受天气状况影响而出现的功率波动。而短时间尺度的波动为直驱型海浪发电系统所特有，即使波浪的周期、幅值都保持不变，电机在往复运动中的速度也在不断变化，使得波浪发电产生的电能具有瞬时功率波动频繁，且波动范围大的特点。根据理论推导，这种功率波动的峰均值比不小于2［15］。

文献［15］利用2 台永磁直线电机，搭建了一套2 kW的永磁直驱波浪发电模拟系统实验平台。其中，1 台直线电机作为电动机，模拟动力输出装置的受力;另外1 台电机作为发电机，模拟永磁直线波浪发电机的发电特性。根据文献中给出的实验结果，波浪周期为3 s，波浪幅值约0.5 m，单自由度控制模式下，直驱型波浪发电瞬时输出功率的短时间尺度波动为周期1.5 s、幅值160 W 的正弦波叠加约80 W 的直流分量，如图5 所示。

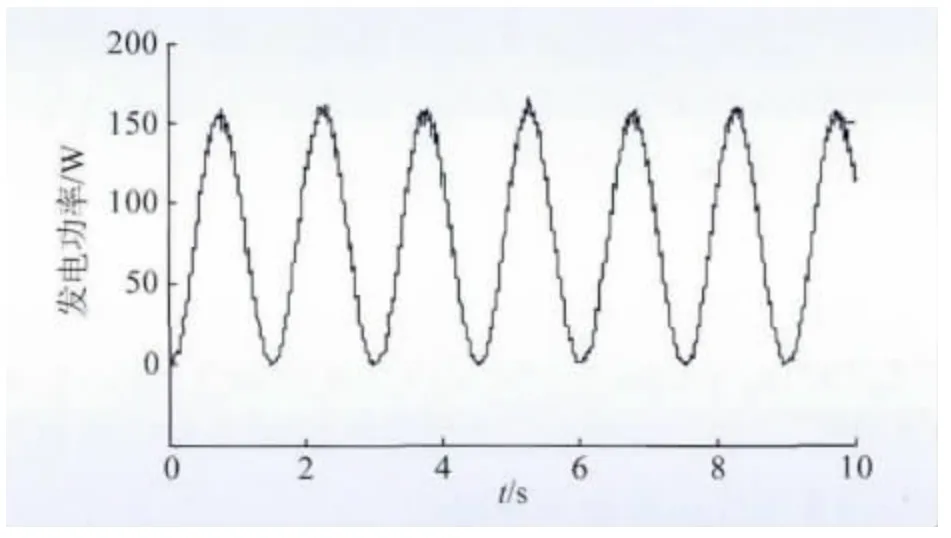
图5 直驱型波浪发电输出功率实验波形Fig.5 Experimental waveform of power output of direct-drive wave power generation

由于波动频率较高，根据式(5)，采用较小容量的超级电容即可对较大幅值的功率波动进行平抑。由于峰均值比较大，如果储能系统中只采用锂离子电池，则在平抑功率波动时锂离子电池可能处于高倍率充放电状态。将锂离子电池与超级电容组合成混合储能系统，则锂离子电池只需处理平均功率与实际所需功率之间的差值，充放电电流可以维持在可接受范围内，有利于延长电池寿命。

根据式(5)，若将图5 所示的功率波动平抑至其平均功率，则所需的超级电容额定储存能量最小值Wmin为

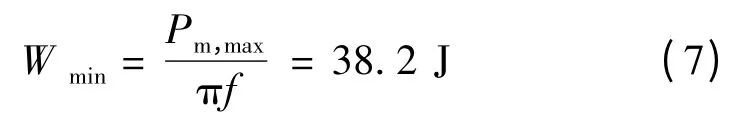
实际应用中，为保证超级电容后端DC/DC 变换器的正常工作，需对超级电容端电压进行限制，比如令超级电容正常电压范围为50% ～100%额定电压。在这一限制条件下，超级电容最多能够吸收或放出75%的能量，此时实际采用的超级电容应在上述计算结果的基础上进行一定的扩容。

上面的算例针对的是超级电容对小容量直驱型波浪发电机在一定浪高和波浪频率下输出功率波动的平抑。实际工程应用中，如海浪的浪高或波浪频率、发电机容量等参数发生变化，造成功率波动的频率或幅值发生变化，则所需的超级电容容量也随之变化。应综合统计各种气象条件下波浪参数的分布范围，然后推算出满足系统正常运行要求的超级电容容量。

对于以风力发电或光伏发电为微电源的微电网，混合储能系统中的超级电容容量也可以根据类似的方法进行设计。

3 结 论

在超级电容和锂离子电池分别经DC/DC 变换器升压后并联的混合储能系统中，超级电容由于能量单价远高于锂离子电池，一般无法提供长时间的功率支撑，但能够承担短时高倍率的充放电任务，从而减小电池的充放电电流和循环次数来延长电池使用时间。通过对该系统的分析，得出以下结论:

(1)基于超级电容较好的功率特性，可采用使电池调节超级电容荷电状态，从而使超级电容直接响应储能系统整体功率指令的功率分配方法。

(2)尽管混合储能系统的功率响应速度受到DC/DC 变换器限制，但在该功率分配方法下，可通过减小超级电容对应DC/DC 变换器的输入电感来提高储能系统整体的功率响应速度。

(3)采用该功率分配方法时，若利用超级电容将某段时间内的功率波动平抑成该段时间内的功率平均值，则可直接通过该段时间内功率波形对时间的积分得到所需的超级电容容量，为超级电容的容量设计提供一定依据。

［1］周林，黄勇，郭珂，等．微电网储能技术研究综述［J］． 电力系统保护与控制，2011，39(7):147-152．

［2］Babazadeh H，Gao W Z，Wang X Y． Controller design for a hybrid energy storage system enabling longer battery life in wind turbine generators［C］//North American Power Symposium (NAPS)，Boston:IEEE，2011:1-7．

［3］唐西胜，齐智平． 超级电容器蓄电池混合电源［J］． 电源技术，2006，30(11):933-936．

［4］董博，李永东，郑治雪． 分布式新能源发电中储能系统能量管理［J］．电工电能新技术.2012，31(1):22-25．

［5］张国驹，唐西胜，齐智平．超级电容器与蓄电池混合储能系统在微网中的应用［J］．电力系统自动化，2010，34(12):85-89．

［6］Liu F C，Liu J J，Zhang B，et al． Energy management of hybrid energy storage system (HESS)based on sliding mode control［C］//Proceedings of the 7th Power Electronics and Motion Control Conference (IPEMC)，Haerbin，China:IEEE，2012:406-410．

［7］易虎．微电网储能技术研究［D］．北京:清华大学，2011．

［8］吴红斌，陈斌，郭彩云．风光互补发电系统中混合储能单元的容量优化［J］．农业工程学报，2011，27(4):241-245．

［9］唐西胜，齐智平．独立光伏系统中超级电容器蓄电池有源混合储能方案的研究［J］．电工电能新技术.2006，25(3):37-41．

［10］张彩萍，姜久春，张维戈，等．梯次利用锂离子电池电化学阻抗模型及特性参数分析［J］．电力系统自动化.2013，37(1):54-58．

［11］戴海峰，魏学哲，孙泽昌． 基于等效电路的内阻自适应锂离子电池模型［J］．同济大学学报:自然科学版，2010，38(1):98-102．

［12］林根德．超级电容在可再生能源系统中的应用及评价［D］． 合肥:合肥工业大学，2012．

［13］吴赟，蒋新华，解晶莹． 锂离子电池循环寿命快速衰减的原因［J］．电池，2009，39(4):206-207．

［14］Choi S S，Lim H S． Factors that affect cycle-life and possible degradation mechanisms of a Li-ion cell based on LiCoO2［J］．Journal of Power Sources，2002 (111):130-136．

［15］康庆．带储能单元的直驱式波浪发电关键技术研究［D］． 北京:清华大学，2013．