考虑风电出力不确定性与半绝对离差风险的机组组合模型
李 嘉,何光宇,刘 锋,胡剑琛,顾志东,魏国清
(1. 电力系统国家重点实验室(清华大学电机系),北京市100084;2.海南电网公司调度通信中心,海口市570203)
0 引 言
传统的机组组合往往在确定性的模型下最小化运行总费用。在风电-火电系统中,采用确定性方法不能有效地处理风电出力的不确定性,若机组组合策略安排不当,会引起电力系统实际运行成本严重偏离期望成本。2012年中国新增风电装机容量接近16 GW,年增长20.4%,总装机容量达到78 GW,中国已经成为全球风电装机容量最多的国家[1]。根据相关规划,2020年我国将建成8个千万kW 级风电基地,届时全国风电装机容量将超过150 GW[2],如何在不确定情形下进行决策将成为新的重大挑战。
在风电-火电系统中,目前针对风电出力不确定性的决策方法大致可分为:
(1)确定性决策方法。一种思路是将风电出力预测误差转变为对正、负旋转备用的需求参数的选择[3]。由于风电出力预测误差随着预测周期的增加而不断增大,为反映这一影响,文[3]中正、负旋转备用容量根据不同研究时段按等比例增长规律选取。另一种思路是先暂不考虑风电出力的不确定性,根据风电出力预测值求得适当机组组合策略;随后将风电出力的不确定性用若干情景进行模拟;再针对每一情景,对所求得的机组组合方案进行安全校核,若校核不通过,则在原机组组合问题中添加相应约束后再行求解,以得到新的机组组合方案[4]。
(2)机会约束规划。机会约束规划允许所做决策在一定程度上不满足约束条件,但该决策使约束条件成立的概率不小于某个置信水平[5]。文献[6]采用机会约束规划,求解了考虑负荷、风电出力、火电机组运行不确定性的机组组合问题,所提方法中允许电力供需平衡在小概率下可不满足。文献[7]提出了一种机会约束两阶段随机规划模型,以保证风电能够以较高的比例被利用。文献[8]考虑了灵活机组和风电,并将机会约束模型转化为非线性整数规划问题。
(3)期望值模型。这是文献中普遍采用的方法,其思想是将可再生能源出力、负荷不确定性用不同情景(或情景树)来表示,则每情景下系统运行费用可视为随机变量,然后建立以调度期间内系统运行费用期望值最小为目标函数的随机优化模型并进行求解[9-13]。文[14]基于极限场景集考虑了多风电场并网的问题。
(4)考虑决策风险。文[15]将风险价值(VaR)和条件风险价值(CVaR)理论融入到含有风电场的机组组合模型中,在最小化运行成本的同时,降低风电的不确定性给系统带来的风险。这在传统的机组组合中很少考虑。
为了考虑风电出力的不确定性,并进行决策风险的管理,本文在文献[16]的基础上,通过情景生成与情景削减的方法来描述风电出力的不确定性,结合投资组合中的均值-半绝对离差模型,提出一种利用半绝对离差衡量决策风险的机组组合模型,以同时考虑运行成本期望和决策风险,并通过算例进行验证。
1 风电-火电系统机组组合问题主要难点
风电出力的不确定性给机组组合带来的主要问题有二,一是如何表征风电出力的不确定性,二是在不确定情形下如何决策。
1.1 不确定性表征
风电出力依赖于多变的天气情况,难以准确预测,风电出力的不确定性是风电-火电系统机组组合的主要困难。虽然近年来风电预测技术不断进步,但其预测精度仍无法满足机组组合的要求。
情景生成(scenario generation)方法常被用于表征风电出力的不确定性,基于预测数据,采用一定的方法生成大量情景,一个情景表征一种可能的确定性情形。
本文基于风电预测数据和统计规律,采用拉丁超立方采样(latin hypercube sampling,LHS)[17]方法产生大量的情景。研究表明,LHS 能够比蒙特卡洛方法更好地近似正态分布[4]。
采用LHS 可以产生大量的情景,但对于机组组合而言,若情景数目过多,计算复杂度大,耗时太长;若情景数目过少,则模拟结果的精度不高,可能遗漏一些具有代表性的情景。为了克服这个问题,可以运用情景削减(scenario reduction)技术。情景削减是一种降低情景集合规模的方法,削减出现概率较小的情景并合并相似的情景,从而找到一个规定基数的情景子集,使得该子集和初始情景集合按照一定的概率距离(probability metric)计量[17-19]是最为接近的。这样在减少优化模型计算量同时也不失情景集合的代表性。
本文采用基于Kantorovich 距离的情景削减技术[19],使得削减后的情景集合能够以较少的情景数目最大程度地近似原始情景集合。
1.2 不确定情形下决策
投资组合理论中称投资结果对期望收益的偏差为投资风险。在风电-火电系统中,若机组组合策略安排不当,风电出力的不确定性可能导致系统运行的实际成本严重偏离期望成本,借鉴投资组合中的概念,称其为机组组合的决策风险。对于实际运行成本高于期望成本的情景,称之为坏情景。最小化期望成本的模型无法反映出潜在的决策风险,当坏情景发生时,可能导致巨大的损失。因此有必要在进行机组组合决策时考虑决策风险。
在投资组合理论中,常用的是Markowitz 提出的均值-方差模型(mean variance,MV),该模型以方差来衡量风险。1991年,Konno 和Yamazaki 在均值-方差模型的基础上,用绝对离差代替方差来刻画投资风险,提出了均值- 绝对离差模型(mean absolute deviation,MAD)[20],将Markowitz 的模型从二次规划转化为线性规划模型[21]。然而投资行为学指出,投资者往往在实际收益低于期望收益时才认为存在风险[22]。上述2 种模型将偏离期望值的正部和负部同等对待,无法反映投资者的风险偏好。徐绪松等于2002年提出了均值- 半绝对离差模型(mean lower semi-absolute deviation,MLSAD)[23],使用半绝对离差计量风险,能够反映投资者的风险偏好,且具有计算优势。
MLSAD 模型简介如下:假设某投资组合问题共有n 种资产,并以随机变量Ri表示第i 种资产的投资收益率(i = 1,…,n),以ri表示Ri的期望,xi表示总投资金额中用于第i 种资产的比例。则在投资组合x = [x1,…,xn]T下的总收益率R(x)为
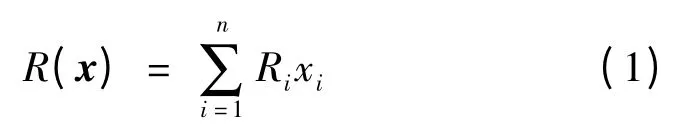
对任意实数v,其半绝对离差定义为
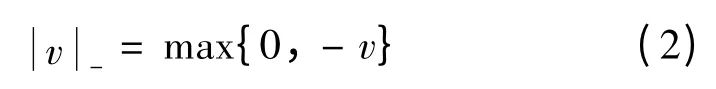
风险L -(x)以半绝对离差计量为

则MLSAD 模型的数学描述为
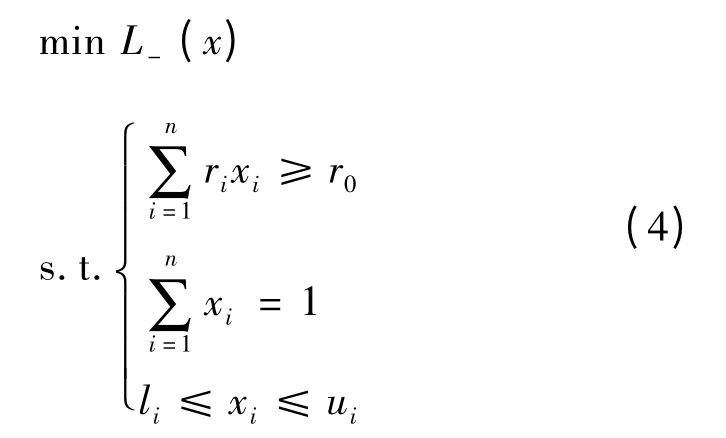
式中:r0为投资者要求的最低回报;实数ui和li为xi的上下界。
考虑如下所示的MLSAD 优化问题
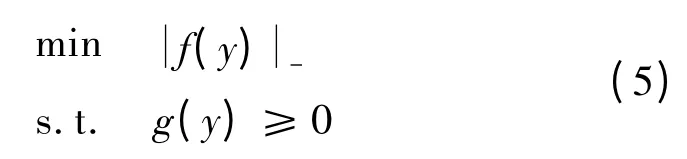
式中:y 是实数;f(y)和g(y)是标量函数。该优化问题等价于如下的简单形式
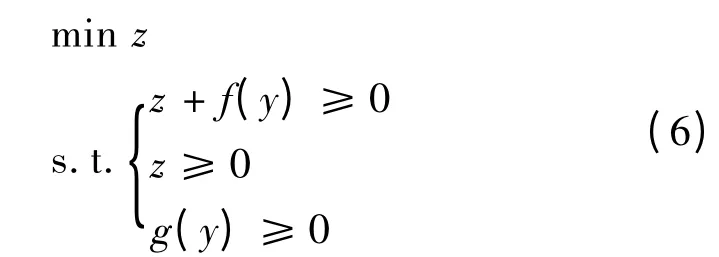
基于这种思想,可以将MLSAD 优化问题转化为简单的形式,并具有计算优势。
MLSAD 模型已被应用于电力系统中[16,24],本文采用半绝对离差计量风险,在满足一定成本期望约束的情况下,以最小化决策风险作为优化目标。
2 风电出力不确定情形下的机组组合模型
2.1 考虑决策风险的机组组合
采用情景生成与情景削减的方法,可将风电出力的不确定性用若干个情景表征。
模型以最小化各个情景中运行费用的半绝对离差期望值为优化目标(decision risk minimization,DRM),从而降低风电-火电系统中机组组合的决策风险。然而决策风险的减小会导致运行成本期望的增加,因此需要添加运行成本期望约束,以保证运行成本期望值不超过电网运营者可接受的水平。
对单个情景,参照文献[25],建立了混合整数线性规划的机组组合模型,约束条件包括系统负荷平衡及旋转备用约束、机组出力限制及爬坡约束、最小起停时间约束。
在各个情景中,虽然同一火电机组在相同时段的起停状态相同,但其出力并不相同。由于最终下发的计划值为确定的值,因此需要添加调整量约束,保证各情景中火电机组实际出力与下发的计划值相近,
2.1.1 目标函数
目标函数为最小化各个情景中运行费用的半绝对离差期望值,即
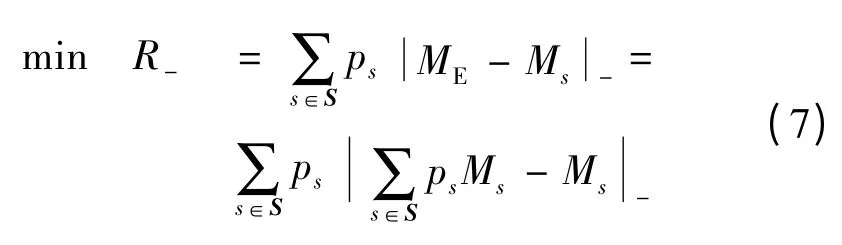
式中:R -表示半绝对离差风险;S 表示情景削减之后的情景集合;ME为该集合中所有情景运行费用的期望值;ps表示情景s 发生的概率;Ms表示情景s 的运行总费用,其计算式为
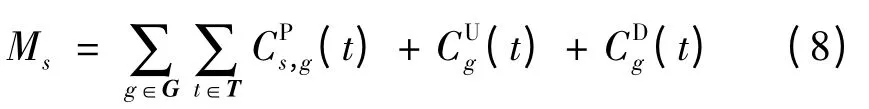
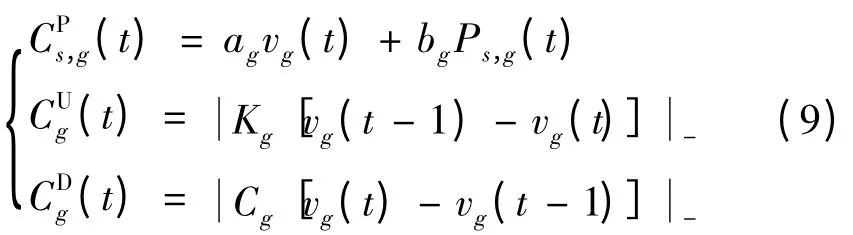
式中:Ps,g(t)为机组g 在t 时段的出力;ag、bg为机组运行成本曲线的相关参数;vg(t)为机组g 在t 时段的状态变量,0 表示关停,1 表示运行;Kg、Cg分别为机组g 起动、停机1次的费用常数。
2.1.2 运行成本期望约束
模型要求运行总费用的期望值不超过电网运营者可接受的水平M0,即满足如下约束
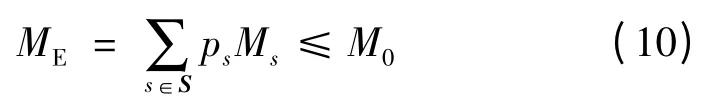
M0由电网运营者根据实际运营情况指定,也可参照不考虑决策风险的机组组合模型的优化结果选取。
2.1.3 调整量约束
由于不同情景中风电出力存在波动,导致最终优化结果中同一火电机组在不同情景相同时段的出力可能不同(起停状态相同),为了保证不同情景发生时,火电机组均能够及时调整出力,以适应风电的波动性,需要添加调整量约束
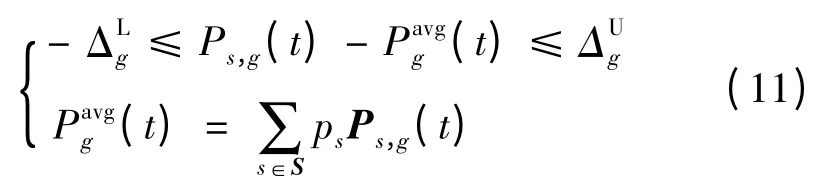
2.1.4 系统负荷平衡
忽略网络损耗,∀S∈S,∀S∈T 满足
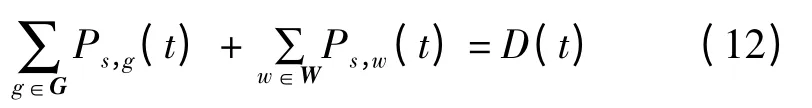
式中:W 为风电机组的集合;Ps,w(t)表示情景s 中风电机组w 在t 时段的出力;D(t)为系统在t 时段的负荷需求。
∀S∈S,∀S∈T,满足
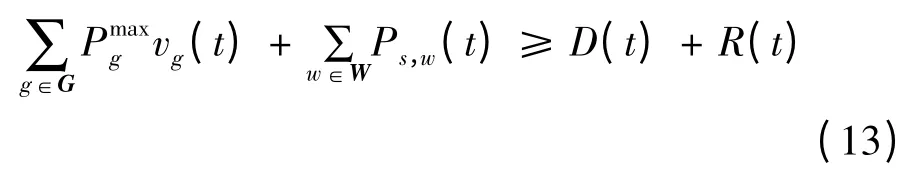
2.1.5 机组出力及爬坡约束
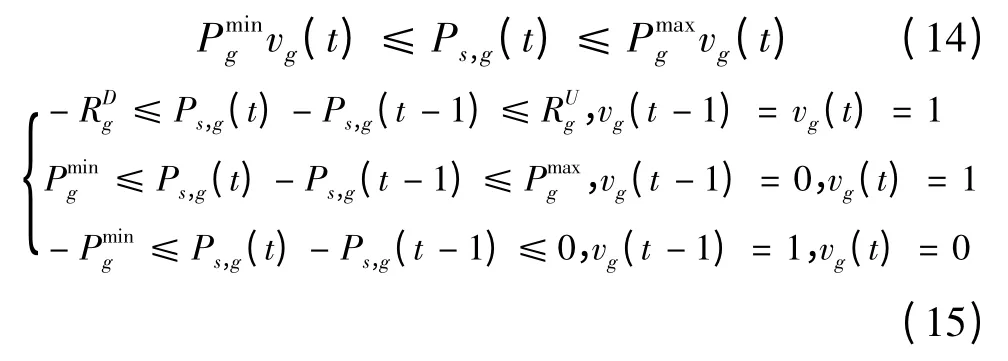
2.1.6 最小起停时间约束
∀g∈G,满足
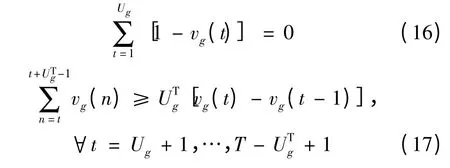
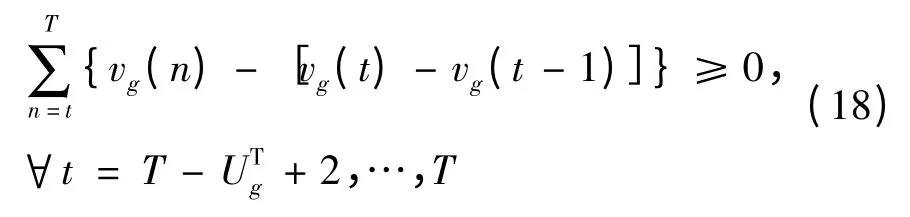
∀g∈G,满足

2.2 不考虑决策风险的机组组合
为突出DRM 模型在决策风险管理方面的优势,作为对比,下面简要介绍最小化运行成本期望(operation cost minimization,OCM)的模型。
OCM 模型的目标函数为最小化所有情景运行费用的期望值

式(22)与式(7)的计量单位相同。
OCM 模型不含运行成本期望约束,其余约束条件均与DRM 模型相同,对模型优化求解之后,类似DRM 模型中取平均值作为最终的调度计划。
不确定性的引入使得风电-火电系统机组组合问题成为一个具有不确定性的大规模混合整数规划的问题,求解难度大。本文将模型线性化,采用CPLEX 算法包对模型进行求解,得到了较好的结果。
3 算例分析
本文通过求解1个含有10 台火电机组、1个风电场的风电-火电系统来验证本文所提机组组合模型的效果,相关数据取自文献[26]。基于Visual Studio 2008 和CPLEX 12.3 编写相关C + +程序进行测试。
系统的调度周期为24 h,以1 h 为单位调度时长。不考虑系统网损及网络约束,假设系统的旋转备用需求为负荷需求的10%,火电机组每min 的爬坡/滑坡速率(RDg)设为机组最大出力的1.5 %,快速调整量取为60 MW。火电机组的相关参数见表A1 和表A2,其中起动费用取为常数。系统负荷需求及风电出力预测数据见表A3。实际运行经验表明,风电预测的时间跨度越长,预测越不准确。算例中假设风电预测的标准差在前4 h 为σ/2,在随后的20 h 为σ,且σ = 0.1。利用LHS 产生5 000个情景,情景削减后保留10个情景,保留情景数据见表A4。
针对上述系统,分别建立了DRM 和OCM 模型算例。DRM 模型算例是为验证其处理运行成本期望和决策风险的效果;OCM 模型算例为前者提供对比,并为DRM 模型提供选取M0的依据。本算例中,OCM 模型的运行成本期望最优值为$435 340,DRM模型的可接受运行成本期望值M0可取为比OCM 模型的运行成本期望最优值稍大的数,这里取为:$435 490。M0的取值对DRM 模型的计算结果有较大影响,后续算例中还将进行重点分析。
3.1 DRM 模型与OCM 模型对比分析
DRM 与OCM 模型优化结果对比结果见表1,DRM 模型的各机组起停情形见表A5。如前所述,各个情景中实际运行成本与运行成本期望值的偏差采用半绝对离差计量,称之为情景的运行风险。当情景的运行成本高于运行成本期望时,存在运行风险,而情景的运行成本低于成本期望时,运行风险为0。情景的运行成本高于运行成本期望值越多,则运行风险越大。
DRM 与OCM 模型在不同情景中的运行风险如图1 所示。可以看出,各情景中DRM 模型的运行风险均低于或等于OCM 模型,尤其是对于坏情景,即实际成本高于期望成本的情景,运行风险的减少更为明显。2 种模型的运行成本期望值相差$150,然而,当坏情景发生时,例如情景6,OCM 模型的运行成本比期望成本增加$11 581,而DRM模型的运行成本比期望成本增加$9 514,DRM 模型的运行成本偏差比OCM 模型减少了$2 067。由此可见,当2 种模型的运行成本期望相近时,OCM 模型并不能反映出潜在的风险,当坏情景发生时会导致运行成本显著增加,而DRM 模型能够减小潜在的风险,使得可能发生的情景的运行成本与运行成本期望更为接近。
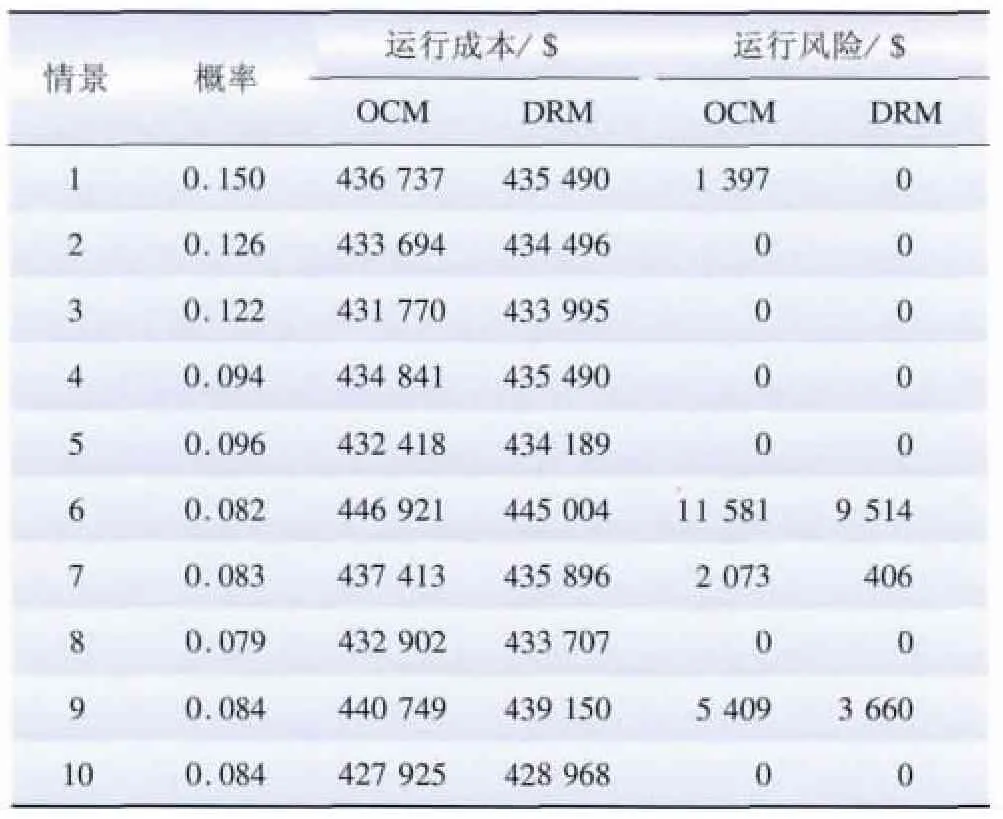
表1 OCM 与DRM 模型运行成本及运行风险对比Table 1 Comparison of operating cost and operating risk in OCM model and DRM model
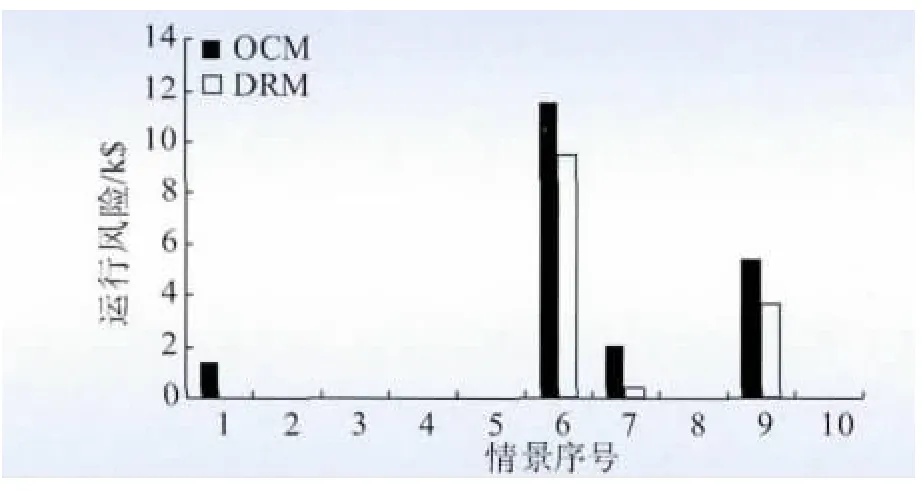
图1 OCM 与DRM 模型不同情景的运行风险Fig.1 Operating risk of OCM model and DRM model in all scenarios
将各个情景运行风险的期望定义为机组组合在不确定情形下的决策风险。DRM 模型的目标为最小化决策风险。从运行成本来看,对于几个发生概率较小而运行成本较高的情景(情景6、7、9),DRM 模型的运行成本都低于OCM 模型;对于大多数的情景,DRM 模型的运行成本与OCM 较为接近。由表1 可计算出OCM 模型的决策风险为$1 785.65 ,DRM模型的决策风险为$1 121.27 。可见DRM 模型在大多数情景中的成本处于可接受的水平内,在成本较高的情景中降低了成本,因此能够在保证运行成本期望不高于可接受水平的前提下,降低决策风险,在风电-火电系统机组组合中能够较好地处理决策风险与运行成本期望间的关系。
3.2 运行成本期望与决策风险的关系分析
改变M0的取值,在不同M0下进行DRM 模型的求解,得到结果如图2 所示。
由图2 可见,可接受运行成本期望水平M0越高,则DRM 模型的决策风险越小,且近似成线性关系,即:M0增加$1 000 ,则最小决策风险减少约$100 。这与一般认识是一致的。因此电网决策者可以通过调整运行成本期望的可接受水平来减小决策风险,从而更好地权衡运行期望和决策风险之间的关系。

图2 最小决策风险与运行成本期望的关系Fig.2 Relationship between minimum decision risk R -and M0
4 结 论
本文提出了基于半绝对离差风险的风电-火电系统机组组合模型,以同时考虑系统运行成本期望和决策风险。通过算例分析,得到以下结论:
(1)最小化期望成本的OCM 模型不能反映可能存在的决策风险,而DRM 模型能够较好地表征潜在的决策风险,反映电网运营者的风险偏好。
(2)在大多数情景中,DRM 模型能够得到较好的决策方案,而在坏情景中,DRM 模型的决策方案能够将决策风险限制在可接受的范围之内。
(3)DRM 模型能够较好地权衡运行成本期望与决策风险之间的矛盾关系,为风电-火电系统的机组组合提供了新的思路。
[1]郭飞,王智冬,王帅,等. 我国风电消纳现状及输送方式[J]. 电力建设,2014,35(2):18-22.
[2]黄强.含大规模风电的电力系统有功平衡问题研究综述[J]. 电力建设,2013,34(4):27-31.
[3]周玮,彭昱,孙辉,等. 含风电场的电力系统动态经济调度[J].中国电机工程学报,2009,29(25):13-18.
[4]Wang J, Shahidehpour M, Li Z. Security-constrained unit commitment with volatile wind power generation[J]. IEEE Transaction on Power Systems,2008,23(3):1319-1327.
[5]Beyer H G,Sendhoff B. Robust optimization-A comprehensive survey [J]. Computer Methods in Applied Mechanics and Engineering,2007,196(33 -34):3190-3218.
[6]Ding X Y,Lee W J,Wang J X,et al. Studies on stochastic unit commitment formulation with flexible generating units[J]. Electric Power Systems Research,2010,80(1):130-141.
[7]Wang Q,Guan Y,Wang J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output[J]. IEEE Transaction on Power Systems,2012,27(1):206-215.
[8]丁晓莺,刘林,王锡凡,等. 考虑灵活运行机组的随机机组组合模型[J].电力系统自动化,2009,33(18):23-27.
[9]Pappala V S,Erlich I. A new approach for solving the unit commitment problem by adaptive particle swarm optimization[C]//Proceedings of the Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century.Pittsburgh,PA:IEEE:2008:1-6.
[10]Pappala V S,Erlich I,Rohrig K,et al. A stochastic model for the optimal operation of a wind-thermal power system[J]. IEEE Transaction on Power Systems,2009,24(2):940-950.
[11]Pappala V S,Erlich I. A variable-dimension optimization approach to unit commitment problem[J]. IEEE Transaction on Power Systems,2010,25(3):1696-1704.
[12]Pappala V S,Erlich I,Singh S N. Unit commitment under wind power and demand uncertainties[C]//Proceedings of the Power System Technology and IEEE Power India Conference. New Delhi:IEEE:2008:1-6.
[13]颜拥,文福拴,杨首晖,等. 考虑风电出力波动性的发电调度[J]. 电力系统自动化,2010,34(6):79-88.
[14]叶荣,陈皓勇,王钢,等. 多风电场并网时安全约束机组组合的混合整数规划解法[J],电力系统自动化,2010,34(5):29-33,65.
[15]任博强,蒋传文,彭鸣鸿,等. 基于改进遗传算法的含风电场的电力系统短期经济调度及其风险管理[J]. 现代电力,2010,27(1):76-80.
[16]Zhang X,He G,Lin S,et al. Economic dispatch considering volatile wind power generation with lower-semi-deviation risk measure[C]//Proceedings of the 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. Weihai,China:IEEE,2011:140-144.
[17]McKay M D,Beckman R J,Conover W J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics,1979,21(2):239-245.
[18]Growe-Kuska N,Heitsch H,Romisch W. Scenario reduction and scenario tree construction for power management problems[C]//Proceedings of the Power Technology Conference Proceedings.Bologna,Italy:IEEE,2003:1-7.
[19]Heitsch H,Romisch W. Scenario reduction algorithms in stochastic programming[J]. Computational Optimization and Applications,2003,24(2 -3):187-206.
[20]Konno H, Yamazaki H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market[J].Management Science,1991,37(5):519.
[20]Konno H,Koshizuka T. Mean-absolute deviation model[J]. IIE Transactions (Institute of Industrial Engineers),2005,37(10):893-900.
[22]Jarrow R, Zhaou F. Downside loss aversion and portfolio management[J]. Management Science,2006,52(4):558-566.
[23]徐绪松,杨小青,陈彦斌. 半绝对离差证券组合投资模型[J].武汉大学学报:理学版,2002,48(3):297-300.
[24]刘瑞花,刘俊勇,何迈,等. 半绝对离差购电组合优化策略及风险管理[J]. 电力系统自动化,2008,32(23):9-13.
[25]Carrion M,Arroyo J M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem[J].IEEE Transaction on Power Systems,2006,21(3):1371-1378.
[26]Yan Y,Yang S,Wen F,et al. Generation scheduling with volatile wind power generation[C]//Proceedings of the International Conference on Sustainable Power Generation and Supply. Nanjing,China:IEEE,2009:1-7.

