考虑电网运行状态不确定性的最优潮流研究

王 彬，何光宇，卢建刚，向德军

(1. 广东电网电力调度控制中心，广州市510600;2. 上海交通大学电气工程系，上海市200240)

0 引 言

最优潮流(optimal power flow，OPF)是电力系统实时优化调度的重要手段［1］，基本思想是在系统负荷水平、网络结构和网络参数确知的情况下，通过对某些控制变量的优化，找到在满足所有给定约束的前提下，使得系统达到某种准则下最优潮流分布的控制策略［2］。

在面向实时态的控制中，最优潮流往往以系统当前的运行状态作为初始运行状态对某些可控资源进行优化，形成优化控制策略，使得当该控制策略下发并执行后，系统的运行状态在满足给定约束的前提下达到某种准则下的最优。

最优潮流的前提是系统当前的运行状态已知，而基于量测数据或状态估计得到的状态并不等于系统的真实状态，在某些情况下甚至偏离真实状态较远。如果基于不准确的状态进行最优潮流控制，可能使得控制后系统的运行状态不再满足经济上的最优，甚至不再满足安全性的要求。因此，在最优潮流研究中，应考虑系统当前运行状态不可知带来的不确定性。

在确定性最优潮流的基础上，很多学者将不确定性引入到最优潮流中，具体方法包括最优潮流的灵敏度分析［3］，参数化最优潮流(parametric OPF)［4］，模糊最优潮流(fuzzy OPF)［5－6］和随机最优潮流(stochastic OPF)［7－12］等。其中，在随机最优潮流中，不同的学者考虑了不同的不确定性，比如负荷的不确定性［7－8］、发电机出力的不确定性［9－10］、系统拓扑的不确定性［11］、目标函数的不确定性［10］、新能源出力的不确定性［12］等，但在考虑电网运行状态不确定性方面，已有研究尚有所欠缺。

文献［13－14］提出了可信状态估计的概念，在量测数据的基础上分别采用区间约束传播和锥优化模型的方法来求解电网可能的运行状态所隶属的区间，并以此来描述电网运行状态的不确定性。

本文在可信状态估计所得到的状态区间基础上，建立了考虑电网运行状态不确定性的最优潮流的随机规划模型。相比于传统的最优潮流模型，在本章所提模型中，优化前的初始运行状态被定义为隶属于可信状态集合的随机变量，相应地，优化后的运行状态也成为随机变量，而目标函数为优化后运行状态的某种形式性能指标的期望值。采用场景分析的方法将上述随机规划模型转化为确定性的优化模型，求解该模型，可得到可控资源的调整量，该调整量面向所有可能的运行状态，均满足安全性和经济性的要求。

本文第一部分首先在已有最优潮流模型的基础上建立最优潮流的随机规划模型，第二部分将介绍基于场景分析求解该模型的方法，最后将通过不同的测试算例说明本文所提方法的有效性。

1 模型建立

1.1 已有最优潮流模型

常规最优潮流的数学模型可表示为

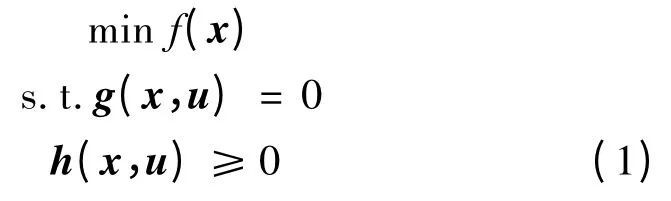
式中:x 为优化后系统的运行状态;u 为可控资源对应的优化变量，比如发电机有功出力、机端电压、变压器分接头等;g 为潮流约束;h 为物理运行约束和控制能力约束;对应于不同优化准则，目标函数f 具有不同的形式，比如发电费用、网损、煤耗等。

为分析初始运行状态对最优潮流的影响，将模型(1)转化为

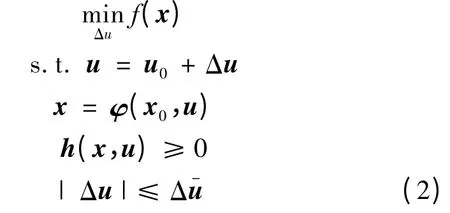
式中:x0为系统优化前的初始运行状态;u0为可控资源的初始状态，其往往和系统的初始运行状态相关，比如发电机有功出力、机端电压等可控变量，本身也是系统运行状态的一部分;Δu 为可控资源的调整量，即控制策略，Δ为单次控制的最大调整量;x =φ(x0，u)为状态转移方程，φ 为状态转移函数，其物理含义为将控制策略Δu 施加到运行状态为x0的系统上后，该系统的运行状态将变为x。由于潮流方程的非线性，φ 一般不能解析地表达，但状态转移方程的概念有利于后续的分析。

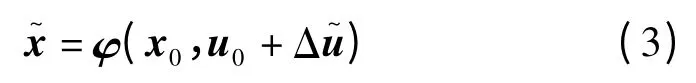
假设系统优化前的真实运行状态为xt，模型(3)中的x0往往根据量测数据或状态估计的结果得到，并不等于真实运行状态(实际上，真实状态xt是不可知的)，即x0≠xt(某些情况下x0偏离xt较远)。相应地，u0≠ut。如果将控制策略Δ施加到实际系统中，其控制后的状态为

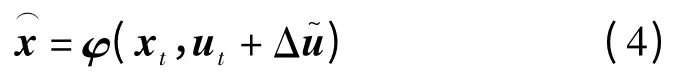
由于x0≠xt，u0≠ut，因此≠。相应地并不能在状态处达到最优，即控制策略Δ对运行状态为xt的系统而言，经济上不是最优的。此外，物理约束同样未必满足，即控制策略Δ对状态为xt的系统而言，未必是安全的。

综上所述，如果在最优潮流中不考虑初始运行状态的不确定性，其优化控制策略既不能保证经济性，也不能保证安全性。

1.2 最优潮流的随机规划模型

虽然系统的真实状态xt未知，但根据文献［13］所提可信状态估计方法，可求得状态区间X，使得xt∈X。因此，可将系统的初始状态设定为隶属于集合X 的随机变量，记为。相应地，可控资源的初始状态同样为随机变量，记为。对于最优潮流而言，优化控制策略，即调整量Δu，必须为确定值，否则无法形成控制指令。根据状态转移方程，优化后系统状态也将成为随机变量，记为xξ。基于此，可将模型(2)转化为:

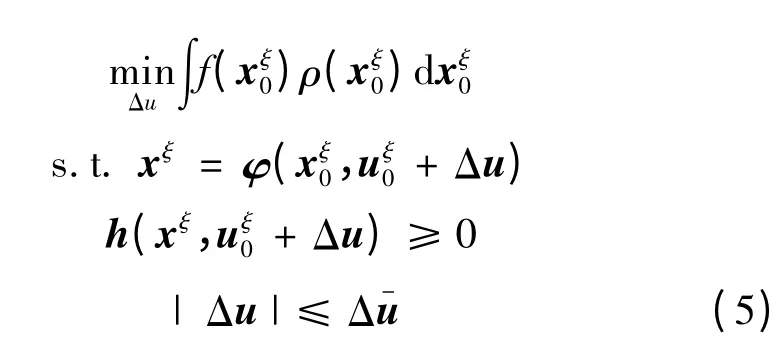
模型(5)为随机规划模型，求解该模型，可得到唯一确定的控制策略Δu，将该策略施加到状态区间X 中的任意状态上，均能使得控制后状态满足约束条件，同时使得所有可信状态下控制后系统的性能指标的期望值最小。

2 模型求解

直接求解随机规划模型(5)比较困难，可通过场景分析的方式将其转化为确定性的优化模型。场景分析包括场景生成和场景消减2 步。

2.1 场景生成

场景生成，即根据随机变量的统计规律，通过随机模拟方法，产生大量样本，每一个样本即为一个场景，代表一种确定性的情形。场景生成本质上是创建随机变量的离散概率分布的过程。最常用的场景生成方法是抽样法，比如蒙特卡罗抽样(Monte Carlo sampling，MCS)、拉丁超立方抽样(Latin Hypercube sampling，LHS)［15］等，其中拉丁超立方抽样方法在特定情况下可显著降低样本的数量。

对于模型(5)，每一个场景均对应系统的一种可能的初始运行状态。不失一般性，假设初始运行状态在集合X 中均匀分布，并用M个场景来描述，其中场景w 对应的概率为pw，系统初始状态为x0w，可控资源的初始状态为u0w。则模型(5)可转化为

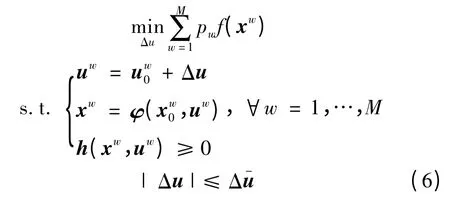
2.2 场景消减

场景生成得到的场景集合Ω 中样本的数量极大，如果直接应用，将严重降低优化问题的计算效率，因此需在场景生成的基础上，对场景集合进行一定程度的消减。场景消减的基本原则是在保留较少场景的情况下又能充分地描述原有随机变量的分布。

文献［16］提出了基于Kantorovich 距离进行场景消减的方法，其基本思路是合并场景集中距离较近的场景，通过最小化初始场景集Ω 和消减后场景集合ΩS(亦称为保留场景集)的Kantorovich 距离，使得保留场景集ΩS能够最大程度地代表初始场景集合Ω。

具体地，初始场景集Ω 和保留场景集ΩS的Kantorovich 距离定义为

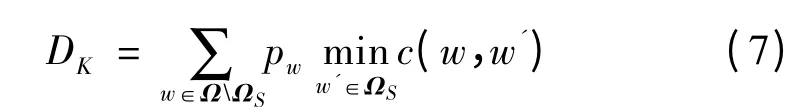
式中:c(w，w')为表征场景w 和w' 距离的函数，也称为代价函数(cost function)。

若ΩS中场景的数量N 给定，则场景消减算法转化为求解:

文献［16］提出了求解上述优化问题的前向算法和后向算法，其中前向算法计算效率更高。在场景消减中，代价函数一般选取为某种范数形势下的距离［17－18］，即

2.3 基于场景的模型的具体形式

以最小化网损的最优潮流为例，给出模型(6)的具体形式。设发电机节点集合为NG，负荷节点集合为ND，选取发电机有功出力PGi和机端电压VGi作为可控变量，即u =［PGi，VGi］，其初值为u0=［P0Gi，V0Gi］，选取状态变量为

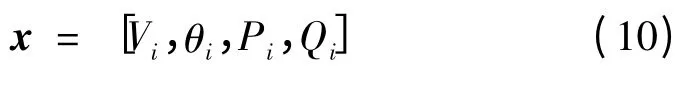
则目标函数为

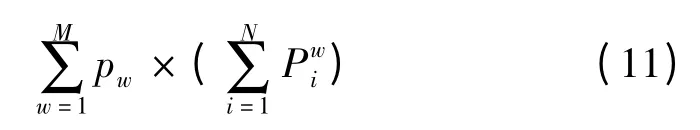
状态转移方程可表征为

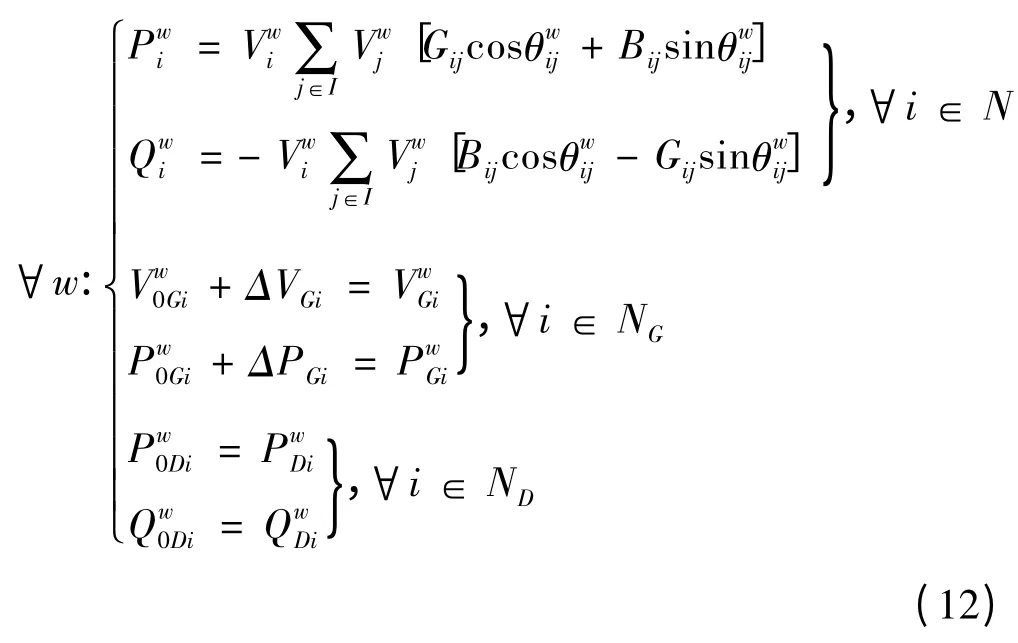
电力系统运行的物理限值约束为

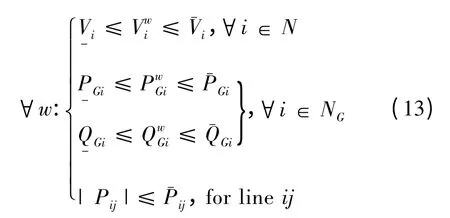
控制变量的调整量约束为

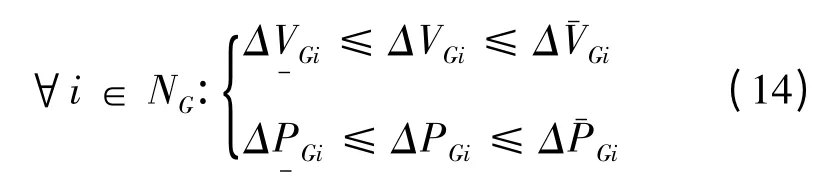
采用原始－对偶内点法来求解上述模型，具有收敛性能好、计算效率高等特点［19－20］。

3 算例分析

本节通过对比本文所提的考虑状态不确定性的最优潮流(简记为US－OPF)和常规基于状态估计结果的最优潮流(简记为T－OPF)得到的结果，说明USOPF 能够在初始运行状态不确知的情况下保证控制策略的经济性和安全性。

分别对IEEE 14 节点系统和IEEE 118 节点系统进行测试。在所有测试中，T－OPF 中的初始状态由最小二乘估计器对量测数据进行状态估计得到，而USOPF 中的状态区间由文献［13］中提出的基于锥规划模型的优化方法求解得到。最优潮流的目标函数设定为最小化系统网损。在标准测试系统中，通过在潮流结果的基础上添加幅值为2%的均匀分布的误差，形成量测数据。相应地，量测误差的界设定为［－0.02zt，0.02zt］，其中zt为潮流解。节点电压幅值的上下限设置为［0.9，1.1］，并作为约束条件加入到最优潮流中。

3.1 IEEE 14 节点系统算例

IEEE 14 节点系统网络图参见图1。在该系统中，节点1 为松弛节点，节点2，3，6，8 为PV 节点，其余节点均为PQ 节点。将节点2，3，6，8 作为可控节点，可控节点上的有功出力和电压幅值作为控制变量。

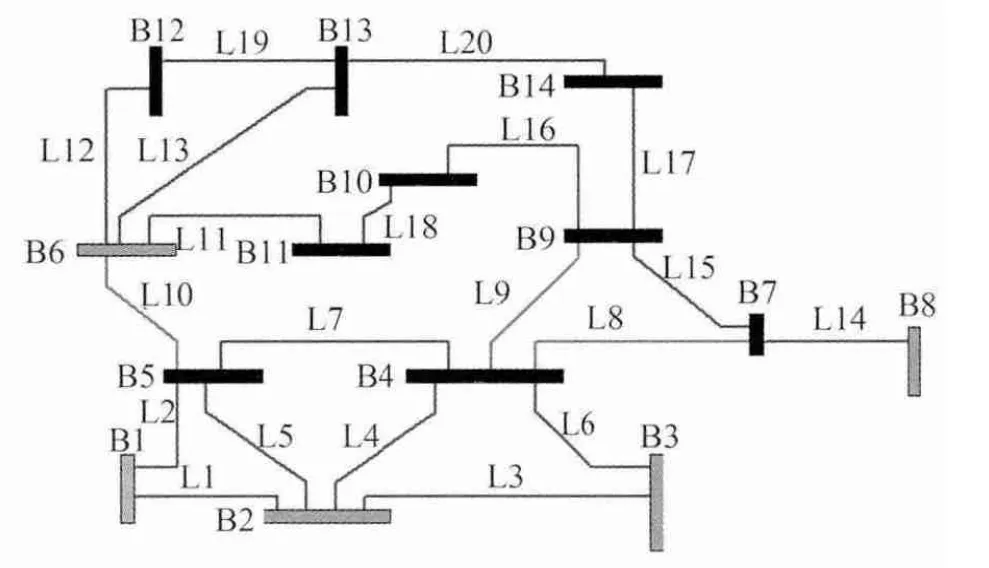
图1 IEEE14 节点系统网络图Fig.1 Network of IEEE 14-bus system

首先，在状态区间中通过LHS 抽样产生100个场景，并基于代价函数(9)进行场景消减，消减至10个场景。图2、图3 分别给出了10个保留场景对应的节点电压幅值和节点电压相角，其中虚线部分为保留场景，而实线部分为系统的真实运行状态。

图2 IEEE14 节点系统电压幅值的场景Fig.2 Scenarios of voltage magnitude in IEEE 14-bus system

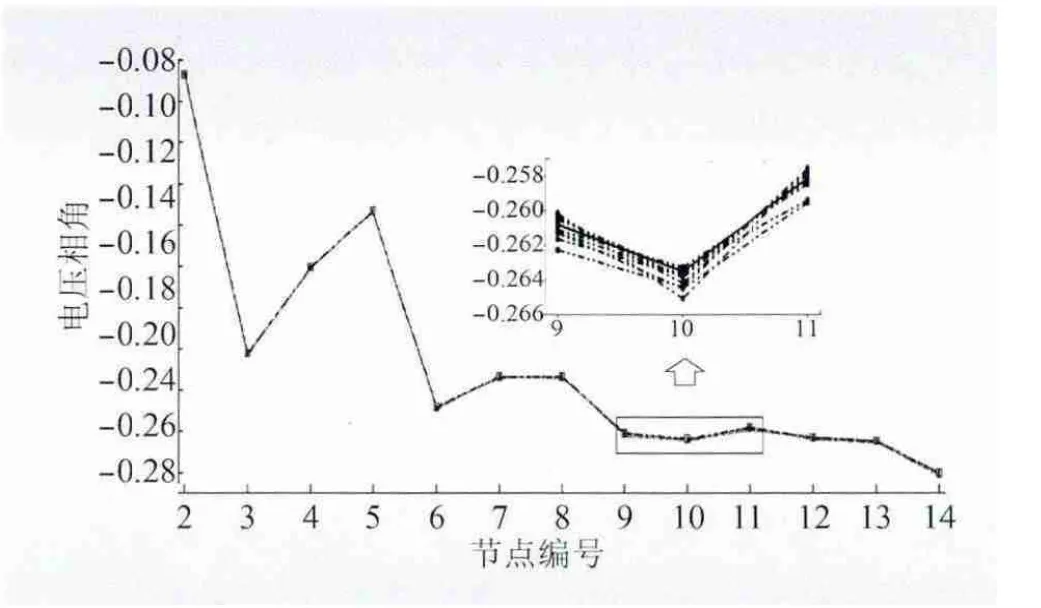
图3 IEEE14 节点系统电压相角的场景Fig.3 Scenarios of voltage angle in IEEE 14-bus system

然后，分别求解US－OPF 和T－OPF，得到的控制策略参见表1。为验证控制策略的经济性和安全性，将控制策略施加到系统的真实状态上，则控制策略执行后系统的状态参见表2。

表1 不同最优潮流方法得到的控制策略Tab.1 Control adjustments obtained by different OPF methods

其中，将T－OPF 得到的控制策略执行后，节点8的电压幅值为1.102 2，超出为电压幅值的限值，即T－OPF得到的控制策略，相对于系统的真实状态，是不安全的。虽然S－OPF 在模型中考虑了节点电压约束，但其针对的是估计状态，而非系统真实状态，因此其控制策略的安全性自然无法保证。相比而言，将US－OPF 得到的控制策略执行后，节点8 的电压幅值为1.087 3，满足电压幅值的限值约束。

表2 不同最优潮流方法对应的控制后状态Tab.2 State under control of different OPF methods

表3 给出了不同最优潮流方法得到的控制后状态对应的网损。从表3 中可以看出，T－OPF 对应的网损较低，但其控制策略不可行。US－OPF 对应的网损虽高，但仅比T－OPF 对应的网损高0.020 MW。因此US－OPF 方法在保证安全性的同时较好地保证了经济性。

表3 IEEE 14 节点系统不同最优潮流方法对应的网损Tab.3 Power loss of IEEE 14-bus system in different OPF methods MW

3.2 IEEE 118 节点系统算例

在该系统中，存在53个PV 节点，为简化起见，将所有PV 节点均作为可控节点，此外将电压的调整范围设置为±0.05pu，PV 节点的有功出力调整范围设置为±20 MW。

同样对该系统进行2 种最优潮流方法的计算。T－OPF 对应的控制后状态虽然不存在越限的情况，但存在2个节点，其电压幅值濒临越限，具体参见表4。以节点10 为例，T－OPF 对应的控制后电压幅值为1.099，与上限1.1 非常接近，安全裕度很低，而US－OPF对应的控制后电压幅值为1.094，安全裕度高。实际上，如果初始运行状态下的电压水平更高，则T－OPF的控制策略极可能是不安全的。

表4 不同最优潮流方法对应的濒临越限点Tab.4 Buses whose voltage magnitude is close to limits in different OPF methods

表5 给出了不同最优潮流方法得到的控制后状态对应的网损。与IEEE 14 节点系统的测试结果类似，US－OPF 对应的网损较高，但仅比T－OPF 对应的网损高0.144 MW，说明US－OPF 的控制策略对系统的真实状态仍具有良好的经济性。

表5 IEEE 118 节点系统不同最优潮流方法对应的网损Tab.5 Power loss of IEEE 14-bus system in different OPF methods MW

综上所述，U－OPF 得到的控制策略在保证安全性的前提下，具有良好的经济性。

4 结 语

本文建立了考虑电网运行状态不确定性的最优潮流的随机规划模型，并采用场景分析的方法将其转化为确定性的优化模型。求解该模型，可得到可控资源的调整量，该调整量面向所有可能的初始运行状态，均满足安全性和经济性的要求。

［1］万黎，袁荣湘. 最优潮流算法综述［J］. 继电器，2005，33(11):80－91.

［2］诸骏伟.电力系统分析［M］. 北京:中国电力出版社，1995.

［3］Gribik P R，Shirmohammadi H S，Thomas C L. Optimal power flow sensitivity analysis［J］. IEEE Transactions on Power Systems，1990，5(3):969－976.

［4］Almeida K，Galiana F P，Soures S. A general parametric optimal power flow［J］. IEEE Transactions on Power Systems，1994，9(1):540－547.

［5］Miranda V，Saraiva J T. Fuzzy modelling of power system optimal load flow［J］. IEEE Transactions on Power Systems，1992，7(2):843－849.

［6］Guan Xiaohong，Edwin Liu W H，Papalexopoulos A D. Application of a fuzzy set method in an optimal power flow［J］. Electric Power Systems Research，1995，34(1):11－18.

［7］Yong Taiyou，Lasseter R H. Optimal power flow under uncertainty［R］. PSERC Report，2000.

［8］胡泽春，王锡凡. 考虑负荷概率分布的随机最优潮流方法［J］.电力系统自动化，2007，31(16):14－19.

［9］Schellenberg A，Rosehart W，Aguado J. Cumulant based stochastic optimal power flow (S－OPF)for variance optimization［C］//Proceedings of IEEE Power Engineering Society General Meeting，2005.

［10］Schellenberg A， Rosehart W， Aguado J. Cumulant－based probabilistic optimal power flow (P－OPF)with Gaussian and Gamma distributions［J］. IEEE Transactions on Power Systems，2005，20(2):773－781.

［11］Capitanescu F，Glavic M，Ernst D，et al. Contingency filtering techniques for preventive security－constrained optimal power fow［J］. IEEE Transactions on Power Systems，2007，22 (4):1690－1697.

［12］廖迎晨，甘德强，陈星莺，等. 考虑分布式电源出力不确定性的城市电网模糊最优潮流分析［J］. 电力自动化设备，32(9):35－39.

［13］Wang Bin，He Guanyu，Liu Kaicheng. A new scheme for guaranteed state estimation of power system［J］. IEEE Transactions on Power Systems，2013，28(4):4875－4876.

［14］Wang Bin，He Guanyu，Liu Kaicheng，et al. Guaranteed state estimation of power system via interval constraints propagation［J］.IET Generation，Transmission ＆ Distribution，2013，7 (2):138－144.

［15］Helton J C，Davis F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems［J］.Reliability Engineering ＆System Safety，2003，81(1):23－69.

［16］Heitsch H，Römisch W. Scenario reduction algorithms in stochastic programming［J］. Computational Optimization and Applications，2003，24(2):187－206.

［17］Dupaˇcová J，Gröwe－Kuska N，Römisch E. Scenario reduction in stochastic programming:an approach using probability metrics［J］.Math Program Seris A，2003(95):493－511.

［18］Gröwe－Kuska N，Heitsch H，Römisch W. Scenario reduction and scenario tree construction for power management problems［C］//Proceedings of IEEE Power Technology Conforence，Bologna，Italy，2003.

［19］Wöchter A，Biegler L T. On the implementation of an interiorpoint filter line－search algorithm for large－scale nonlinear programming［J］. Mathematical Programming，2006，106(1):25－57.

［20］谢亮，基于内点理论最优潮流的算法及应用研究［D］. 上海:上海交通大学，2011.