基于复杂网络理论的输电容量匹配模型
舒征宇,丁红声,周建华,俞 翰,向 坤
(国网宜昌供电公司调度控制中心,湖北省宜昌市443000)
0 引 言
电力系统是一种典型的广延耗散系统,这种系统在外因和内因的作用下会逐渐演变达到自组织临界状态,容易诱发系统崩溃[1-3]。其重要特征是在复杂大电网中发生的故障规模及其对应的累积概率服从尾幂律分布特性。这一现象也在国内外诸多大型电网的统计数据中得到了验证[4-9]。
针对电网的自组织临界特性,研究人员分析了影响连锁故障发生几率以及故障规模大小的主要因素。其结果显示系统的负载率分布(即输电容量冗余的分配)对于连锁故障的传播尤为重要。文献[10-12]分别对于系统负载率的均衡分布以及负载率的异质分布进行了分析,其中文献[10]建立了复杂电力网络的负荷-容量模型(ML 模型),假定系统中每条输电线路上存在的输电容量冗余与其稳态时的有功潮流成正比。在该模型下的实验结果表明,系统的平均负载率越高,系统越接近自组织临界状态。大规模连锁故障的发生几率会随平均负载率的上升而增加。文献[11]则分析了负载率的异质分布对电网自组织临界特性的影响,提出了潮流熵的概念用于量化负载率分布的异质程度。文中指出连锁故障的传播过程中系统的潮流熵会随之增加,整个系统会向自组织临界态进行演化,从而形成大规模的连锁故障。文献[12]则以连锁故障搜索模型分析了负载分布情况对连锁故障的影响,其结论表明考虑平衡整个系统负载率分布,降低部分重要线路的负载率的措施可以有效降低大规模连锁故障的几率。
以上研究均指出电力网络的负载率分布将直接影响电力系统中连锁故障发生的几率及其对应的故障规模大小,如何优化规划电网建设或安排电网的运行方式使得系统的负载率分布达到最优则是当前需要解决的主要问题。鉴于此,本文提出一种输电线路的重要度评估指标,判断线路对于系统的重要程度,并在此基础上给出了输电容量冗余的匹配模型。藉由该模型匹配线路的输电容量冗余,通过调整系统的负载率分布,以期提高电网抵御连锁故障的能力,降低大规模连锁故障发生的几率。
1 基于熵理论的输电线路非均质转移指标
根据已有的研究成果可知[12],当电力网络发生连锁故障时,系统的负载率分布将呈现出向非均质特性演化的趋势,故障传播过程中经常会出现部分线路发生过负荷故障,而大量线路处于轻载的情况。当系统面临大规模连锁故障时不能有效抵御故障的传播。因此,本文从预防系统负载率分布向非均质特性演化的角度,给出线路重要度评估的量化指标。
1.1 输电线路的非均质转移指标
本文基于熵理论提出支路负荷的非均质转移指标(以下简称转移评价指标)用于量化支路发生故障时对于网络中剩余支路负载率的非均质变化的促进作用。
1.1.1 熵的定义
熵是混乱和无序状态的一种量度,熵理论主要应用于信息科学、统计物理学等。当系统可能处于几种不同状态,每种状态Xi出现的概率为Pi时,那么该系统的熵则可以表示为
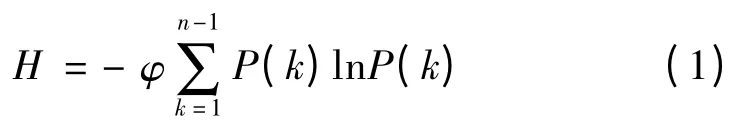
式中:φ 为常数;n 为预先划分的状态数;P(k)为该种状态在系统中出现的概率,其大小为

式中:Xk为系统中所有样本属于状态k 的个数;为总的样本个数。系统的熵越大,其有序程度越低;反之,系统的有序程度越高其熵就越小。若选择系统中输电线路的负载率作为样本,通过式(1)则可以计算出系统负载率的熵。
1.1.2 非均质转移评价指标
根据熵的定义,本文提出输电线路的非均质转移评价指标用于量化输电线路发生故障时对系统负载率非均质分布的促进作用,其计算公式为

式中:HP(eij)为支路eij的转移评价指标,其物理含义为当支路eij传输单位有功负荷且发生故障时,剩余网络中潮流分布变化的熵;Pij(k)为支路eij故障时系统中剩余输电线路传输有功功率的变化比率λ处于λmn(eij)∈(θ·k,θ·k + θ]的概率,其计算公式如式(4),θ 为状态量步长。由于电能输送过程中绝大部分为有功,因此本文只考虑有功负荷的转移。
支路eij故障后剩余网络中任意输电线路emn传输有功的变化比率λmn(eij),其计算公式为

式中:ΔFij(emn)为支路eij在传输单位有功时,发生故障后emn上产生的负荷增量;ΔFavgij则为剩余子网中所有支路上有功负荷增量的均值;ymn为支路emn的导纳,Zij为支路eij断开以后网络的阻抗矩阵。Xij为第i个元素为1,j个元素为-1 的n 维向量,n 为网络节点总数; Xij= [ 0 … 1 … -1 … 0];的物理意义为支路eij断开以后,电网等效成无源网络单位负荷从节点i 注入从节点j 流出时,支路emn上传输的负荷大小;Fmn为系统稳态时输电线路的有功功率;Q 为初始状态下网络中包含的输电线路总数;状态量步长默认取值为
1.2 线路非均质转移指标与稳态潮流比较
以IEEE300 节点典型算例为例,本文计算系统中输电线路的转移评价指标以及对应的稳态有功,按照转移评价指标排序后的前15 位的结果如表1所示。

表1 转移评价指标排序结果Tab.1 Sorting results of transfer evaluated index
根据转移评价指标的物理意义可知,当输电线路传输负荷大小相同时,转移评价指标越高的线路出现过负荷故障给电网带来的扰动越大,将促进网络中负荷分布向非均质分布演化。因此在故障传播的过程中应当尽量避免转移评价指标较高的支路出现过负荷故障。
然而由表1 的计算结果可知,在电力网络中潮流的分布受到电源节点的出力大小、负荷节点的负荷需求以及节点的分布位置影响,转移评价指标较高的输电线路不一定会传输更高的负荷,如表所中所示的输电线路42 -16、119 -118。按照传统的负荷容量模型,即仅仅根据输电线路稳态时输送的有功潮流来匹配输电线路的运行极限不一定能更好地保护系统中的重要线路[13]。当网络中的重要元件发生故障时,潮流的分布会发生变化,若负荷转移评价指标较高的线路发生过负荷故障时则将促进系统负载率向非均质分布演化,从而促进大规模连锁故障发生。
2 输电容量匹配模型
2.1 一种带控制参数的匹配模型
若要避免负荷转移评价指标较高的输电线路出现过负荷故障,则需要在规划时针对这部分重要线路,提高其输电容量或是在方式编排时降低这部分线路的传输功率,从而防止局部故障在电网中的扩散。
鉴于此本文提出输电线路的输电容量匹配模型,结合电网稳态时的潮流分布以及故障传播过程中输电线路对于电网的重要程度,优化系统中输电线路的运行极限,以期降低大规模连锁故障发生的几率,运行极限匹配模型可以表示为

2.2 基于风险评估的控制参数优化
由于控制参数的取值会改变输电容量的分配,从而影响系统负载率的分布以及抗扰动能力,为解决匹配模型中控制参数的优化取值问题,本节将采用风险评估的方法,量化控制参数在不同取值时系统面临的风险,并以此为依据给出控制参数的优化取值。
2.2.1 停电事故概率密度函数求解
本文采用仿真模拟的方法获取系统停电事故概率密度函数。本文采用文献[14]提出的SOC-PF 仿真模型模拟系统中的故障传播,得到控制参数不同取值时系统故障发生几率和故障规模之间的对应关系。图1 为IEEE300 节点系统在α = 1.5 ,控制参数ρ 分别取值0、0.2、0.4 时,通过反复实验200次后得到的故障规模累计概率分布。图1 中横轴L 为负荷损失即故障规模,纵轴P 为大于该故障规模的累计概率分布,图中的坐标均采用对数刻度。

图1 故障规模-累计概率曲线图Fig.1 Cumulative probability curve of failure scale
根据以上仿真模型计算故障的累积概率分布,对实验结果采用最小二乘法进行线性回归分析,可以得到不同忍耐系数和控制参数下的概率密度函数,具体流程如下。
(1)根据实验结果做线性回归处理,得到故障规模及其发生频率之间的关系:

式中:Q 为故障规模;N(Q)为对应故障规模的发生频次;a、b 为待求常数。
(2)在求得以上关系后,采用故障的频率近似代替随机变量的概率分布F,令:

式中:X 为描述故障规模的变量;N(X)为对应的发生次数。根据实验获得的数据进行回归处理则可以得到概率分布函数:

(3)根据概率分布函数求取概率密度函数:

根据以上步骤则可以获得给定忍耐系数与控制参数时故障发生几率及其对应故障规模的概率密度函数。
2.2.2 基于风险评估的控制参数优化取值
根据上一节介绍的方法可以求取给定忍耐系数与控制参数时电力网络的停电事故概率密度函数p(x),其中x 为停电事故的规模。根据风险测量的一般表达式[15],求解系统在给定参数下的风险度量结果,风险测量的数学表达式为

式中:x 表示故障规模;p(x)为故障规模的密度函数,其物理意义为所有可能大小的停电事故的总的风险。那么根据风险评估的优化控制参数取值求解流程见图2。

图2 控制参数优化取值计算流程Fig.2 Calculation process of control parameters optimization
采用以上流程可以求解系统在不同状态下系统整体的风险评估结果,从而通过对比得出不同忍耐系数时控制参数的优化取值。以IEEE300 节点为例,仿真步长w 设为0.1,求得不同取值时,系统损失负荷的风险评估结果见表2。

表2 IEEE 300 节点系统风险评估结果Tab.2 Risk assessment results of IEEE 300 node system MW
由以上计算结果可以发现,在电网的忍耐系数发生变化时,即系统的输电容量冗余总量(或负荷水平)发生改变时,对应改进模型控制参数的取值也会随之发生变化。例如α = 0.5,1.0,1.5 状态下控制参数的最优取值为0.2,而α = 2.0 状态下的最优取值为0.1。控制参数的最优取值会根据输电容量冗余的多少而变化,根据本节提出的风险评估方法则可以获得控制参数的优化取值,进一步优化系统输电容量冗余的分配。
3 算例分析
采用上一节的方法可以求得风险概率最低时忍耐系数以及控制参数所对应的值,而在确定忍耐系数不变的前提下则可以获得控制参数的最优取值。本文以IEEE300 节点系统为例,对比了系统在匹配模型控制参数取值最优时与负荷-容量模型在蓄意攻击模式和随机攻击模式下故障规模随忍耐系数的变化,其具体方案如下。
(1)蓄意攻击模式:以元件(节点或输电线路)的负荷大小为基础将输电线路进行排序,始终攻击系统中有功负荷最高的输电线路,观察故障的传播。调整系统的忍耐系数,对比按照2 种不同匹配模型配置电网输电容量时,系统对于关键元件的依赖性以及连锁故障规模与忍耐系数(即输电容量冗余)之间函数关系的敏感程度。
(2)随机攻击模式:将系统中所有元件加入列表,从中随机挑选3%的元件作为初始故障,模拟故障在电力网络中的传播,调节忍耐系数,观察故障规模随系统初始状态负荷水平的变化。按照以上步骤重复50次,求得50次实验中平均结果以及方差,绘制误差线。
图3 为蓄意攻击的计算结果,其中横轴为忍耐系数,纵轴为故障后电网的最大连通比例[16],用以反映连锁故障的规模。PM 表示本文提出的优化匹配模型,ML 表示传统的负荷-容量匹配模型的结果。由图3 的仿真可知:本文提出的优化匹配模型可以更好地抵御连锁故障的传播,降低连锁故障的规模,在忍耐系数较低(即输电容量冗余有限)的状态下可以大幅提升网络的连通比率,限制故障的传播。
图4 为随机攻击的计算结果,其中横轴为忍耐系数,纵轴为故障后电网的最大连通比例。由仿真结果可知:本文提出的优化匹配模型与传统的负荷-容量模型一样,都能够较好地抵御网络中的随机故障,采用本文的优化匹配模型后在同一忍耐系数时,系统能够更好地抵御随机扰动。
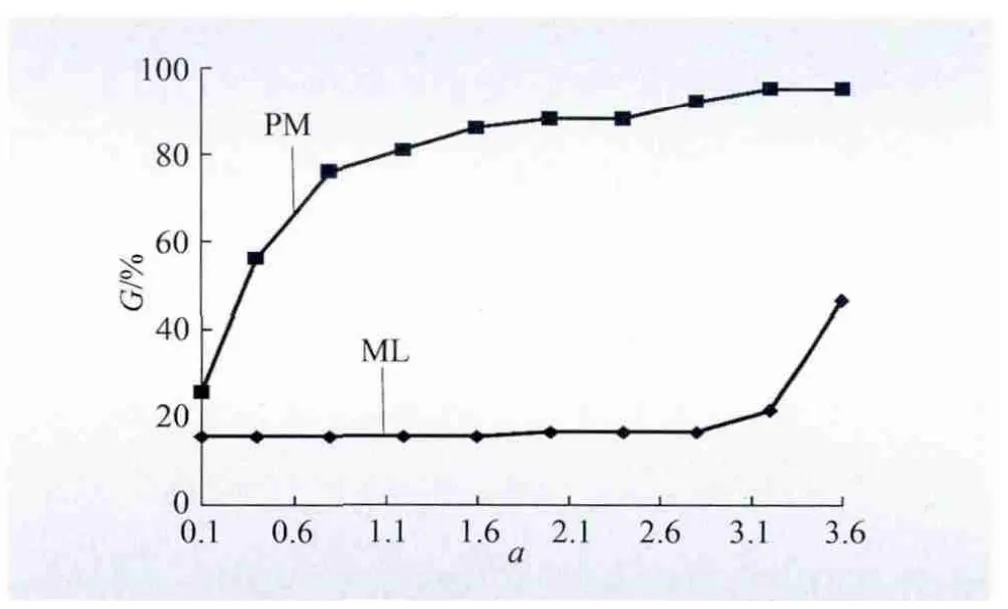
图3 蓄意攻击模式下优化匹配前后对比Fig.3 Comparison before and after optimal matching under deliberate attack

图4 随机攻击模式下优化匹配前后对比Fig.4 Comparison before and after optimal matching under random attacks
对比2 种攻击模式的仿真结果可以发现:按照本文提出的优化匹配模型配置输电线路的输电容量可以更好地防御高负荷元件故障所引发的连锁故障,同时也能够保持系统对于随机故障的鲁棒性。
4 结 论
电力系统输电容量冗余的分布与其脆弱性之间存在直接的关系。合理规划冗余输电容量的分配,防止重要元件发生过负荷故障是预防大规模连锁故障的主要手段。本文从故障传播的角度提出新的重要度评价指标,用于量化输电线路的重要程度,并在此基础上改进了电力系统的运行极限匹配模型,通过在电网规划或方式调整过程中合理配置电网输电容量的冗余,预防故障传播过程中系统的负载率向异质分布的逐渐演化,减少故障传播过程中重要元件出现过负荷故障的几率,从而达到抵御大规模连锁故障发生的目的。仿真实验结果证明,在系统输电容量冗余有限的情况下,该优化匹配模型可以更好地保护系统中的重要元件,有效抵御连锁故障的发生。藉由该匹配模型,电网规划人员可以明确系统存在的薄弱环节,方式编制人员亦可以了解在当前负荷水平下正常运行方式存在的风险。
[1]舒征宇,邓长虹,黄文涛,等. 小世界电力网络故障传播过程与抑制策略[J].电网技术.2013,37(3):861-867.
[2]舒征宇,马俊民,邓长虹,等. 小世界电网的故障传播特性分析与运行极限匹配模型研究[J].电力系统保护与控制,2013,41(7):29-35.
[3]周涛,傅忠谦,刘永伟. 复杂网络上的传播动力学研究综述[J].自然科学进展,2005,5(15):513-518.
[4]丁明,韩平平. 加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报,2008,28(10):20-25
[5]丁明,韩平平. 小世界电网的连锁障传播机理分析[J]. 电力系统自动化,2007,31(18):6-10.
[6]张国华,张建华,杨燕京,等.基于有向权图和复杂网络理论的大型电力系统脆弱性评估[J].电力自动化设备,2009,29(4):21-25.
[7]Holme P,Kim B J,Yoon C N,et al. Attack vulnerability of complex networks[J].Physical Review E,2002(65):056109.
[8]李蓉蓉,张晔,江全元. 复杂电力系统连锁故障风险评估[J].电网技术,2006,5(10):18-22.
[9]倪向萍,梅生伟,张雪敏. 基于复杂网络理论的输电线路脆弱度评估方法[J].电力系统自动化,2008,32(4):1-4
[10]Paul Hines,Seth Blumsack. A Centrality Measure for Electrical Networks [C]//Hawaii International Conference on System Sciences,Hawaii,2008.
[11]曹一家,王光增,曹丽华,等. 基于潮流熵的复杂电网自组织临界态判断模型[J].电力系统自动化,2011,35(7):1-8.
[12]于群,曹娜,郭剑波. 负载率对电力系统自组织临界状态的影响分析[J].电力系统自动化,2012,36(1):24-30.
[13]谢琼瑶,邓长虹,赵红生,等.基于有权网络模型的电力网节点重要度评估[J].电力系统自动化,2009,33(4):21-24.
[14]易俊,周孝信,肖逾男. 电力系统自组织临界特性分析与仿真模型[J].电网技术,2008,32(3):7-12.
[15]周天涛,柳明珠. 风险测量VAR 及其原理[J]. 价值工程,2013,12(36):65-70.
[16]Wang B,Kim B J,A high-robustness and low-cost model for cascading failures[J]. Europhysics Letter,2007,78(4):48001.

