基于改进倍比平滑法的节假日短期负荷预测方法

史文博，王 健，沈添福，边瑞恩

(华南理工大学电力学院，广州市510640)

0 引 言

短期负荷预测通常可以分为正常日负荷预测和节假日负荷预测［1-2］。随着人们生活水平的提高，工作观念和企业用工时间发生改变，节假日负荷表现出与正常日截然不同的变化规律。加之节假日负荷的历史数据少，基于充足历史数据的正常日负荷预测方法很难适用于节假日负荷预测，预测结果的拟合度往往不能满足要求。

为了更准确地预测节假日负荷，为电力部门节假日电力调度提供保障，许多学者就此问题进行了深入研究。文献［3］应用基于三角模糊数的一元模糊线性回归模型对节假日负荷进行预测，由于该方法用待预测日前4 日的负荷数据作为输入，在实际应用中困难较大。文献［4］利用数据挖掘和遗传优化算法建立了一个基于模糊规则的负荷数据模式分类系统，但分类规则复杂。文献［5-7］考虑节假日负荷变化趋势建立神经网络预测模型，由于假节日历史数据贫乏、训练过程不够充分，预测精度难以保证。在短期负荷预测中使用的神经网络和支持向量机算法［8-11］，由于缺乏充足机器学习样本集，难以应用在节假日负荷预测中。文献［12-14］提出了一种基于相似周末的节假日负荷预测方法，考虑日期属性和气象属性选择相似日。文献［15］在相似日选取样本中加入历史节假日，按照相似周末和相似节假日进行修正。但影响因子受气象、地域、人为因素影响较大，在其他区域预测时误差偏大。文献［16］运用对比法研究春节的负荷预测，同样对气象因素加以修正。文献［17］运用多元非线性回归研究台风期间特殊日的负荷预测，主要考虑气象因素的影响。基于以上分析，气象因素修正模型还有待完善，但在预测过程中考虑气象因素影响已成为节假日负荷预测的有效方法。目前，气象敏感负荷在总负荷中所占比重越来越大，提高预测精度的关键是如何更加合理地考虑气象因素对负荷的影响［18-19］。

本文以传统指数平滑法为基础，通过0.618 优选法确定平滑系数［20］，将其运用于节假日负荷预测的基值预测中;同时，在基值预测和归一化曲线预测时，皆引入灰色关联分析法修正气象因素对节假日负荷变动的影响。该模型是适合于节假日负荷预测的归一化预测模型，通过文中提出的样本数据采集方式克服贫乏数据带来的精度不高问题，将归一化日负荷预测应用范围从正常日负荷预测扩展到节假日负荷预测中。将该模型应用于广东省某市2011年节假日短期负荷预测，预测结果具有良好的精度。

1 负荷曲线分析与预测模型设计

基于时序分析的正常日倍比平滑法将预测过程分为标幺曲线预测和基值预测［1］。图1 为广东省某市2010年主要节假日(元旦、春节、五一和国庆)和正常日负荷曲线。

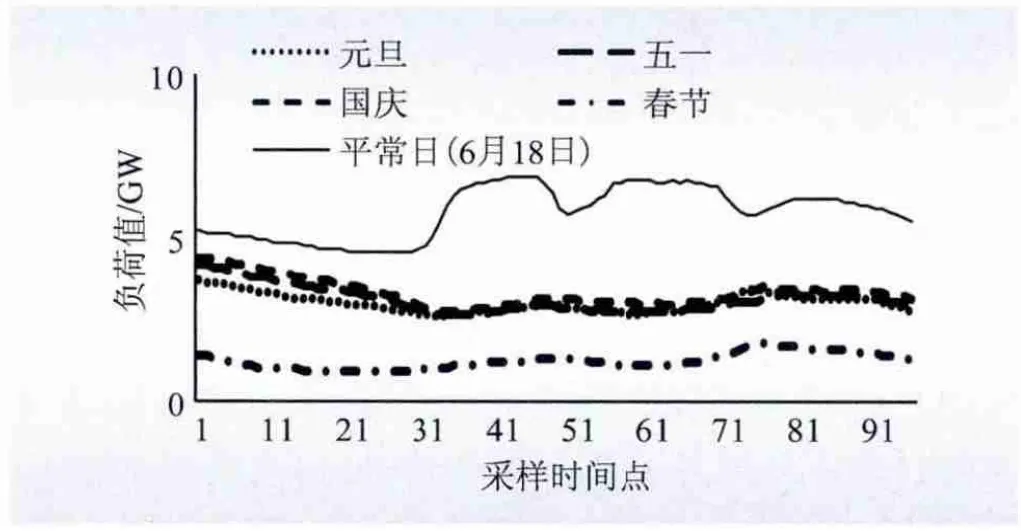
图1 2010年某市节假日与正常日负荷曲线Fig.1 Holiday and normal daily load curves of a city in 2010

从图1 可看出，该市正常日负荷表现出“三峰二谷”的特点，节假日负荷明显低于正常日负荷，并且节假日负荷曲线较平滑，没有明显的峰谷差。在节假日负荷曲线中，春节日负荷曲线低于其他节假日负荷曲线。

同一节假日负荷数据极度贫乏，在同一年里节假日前后较难选取到相似的日负荷曲线。为了满足时序分析倍比平滑法需要大量相似日数据作为样本的特点，本文根据节假日的日期特征，提出节假日负荷预测样本选取方法。

1.1 历史样本集选取方法

历史样本集选取时考虑电力部门通常提前数天进行日负荷预测这一客观事实，具体样本集选取方式如图2 所示。

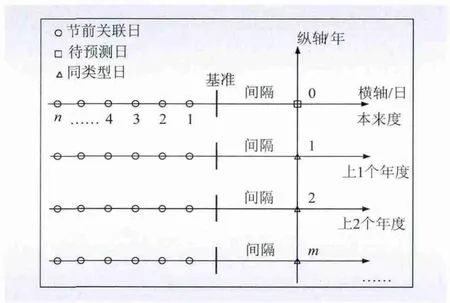
图2 历史样本采集方式Fig.2 Collection method of historical sample

图2 中虚线表示基准日，即电力部门做预测的日期，通常预测间隔约为1 周;取基准日之前的n 天为节前关联日，距离基准日最近的1 天为第1 天，最远的为第n 天，各年的节前关联日天数相同;取m年以来相同节假日为同类型日，图中用三角形表示;本年度节前关联日设为第0 样本集，上1个年度节前关联日和同类型日设为第1 样本集，以此类推，上m个年度样前关联日和同类型日设为第m 样本集。

1.2 同类型日与待预测日的气象关联性分析

为了考虑气象因素对负荷变化的影响，引入灰色关联分析法分析同类型日与待预测日的气象关联性。

设待预测日与第i 样本集的同类型日在第k(k=1，…，r)个气象元素上的差异量Δui(k)为Δui(k)=，将各差异量归一化后的值记为Δu'i(k)，即为

第i 样本集的同类型日在第k个气象元素上的关联度分量ζi(k)为

结合式(1)和(2)，同类型日与待预测日的关联度Ri定义为

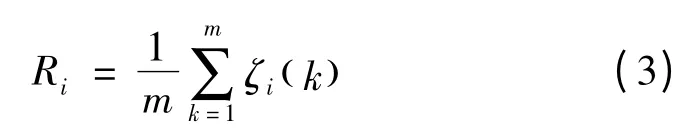
1.3 考虑气象修正的归一化曲线预测

气象因素的变化直接影响每日最大负荷和最小负荷，归一化曲线能够去除年增长率对负荷水平的影响，突出气象因素影响下每日负荷的波动。以春节为例，图3 为该市2006—2011年春节负荷曲线和归一化曲线。

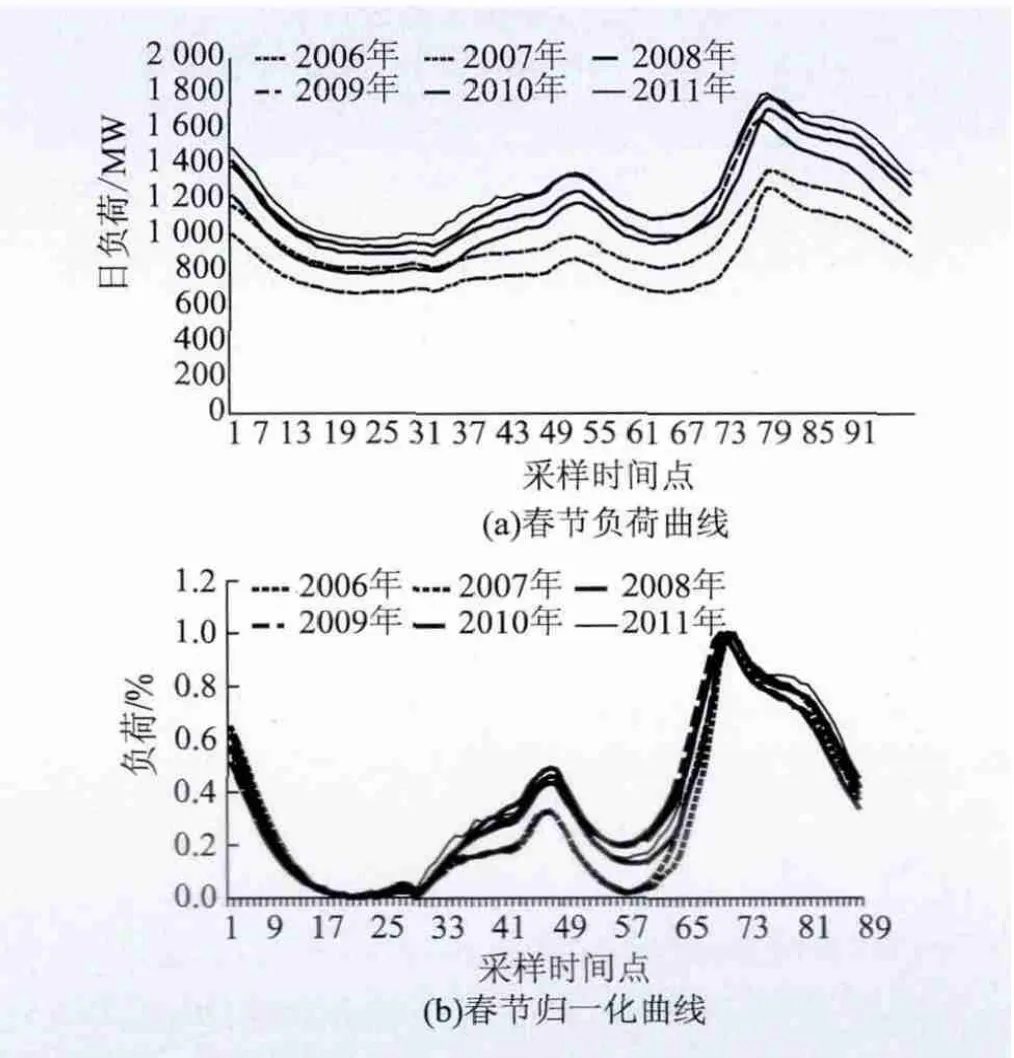
图3 某市2006—2011年春节负荷曲线Fig.3 Load curves of a city in Spring Festival 2006 －2011

由图3(a)可知，受年历史增长率的影响，春节负荷逐年增加。由图3(b)可知，在去除年增长率影响之后，各年春节负荷波动较为相似。但由于气象、特殊事件等不确定因素的影响，每年春节负荷波动并不完全相同。在不确定因素中，气象因素起主要作用，本文在归一化曲线预测时不考虑气象以外不确定因素的影响。预测时直接对归一化曲线进行气象修正，除去气象不确定性，提高预测精度。

对同类型日负荷曲线进行归一化处理，并对归一化曲线进行气象修正，用修正后的曲线作为待预测日的归一化曲线。具体方法如下:

(1)对同类型日的负荷曲线进行归一化计算，得到各年的归一化曲线Li(i =1，…，m)。构造同类型日的气象因素向量U，其中包括r个气象元素。设待预测日气象因素向量为，第i 样本集中同类型日的气象因素向量为

(2)用关联度Ri对各年的归一化曲线Li(i =1，…，m)进行加权修正，用修正得到的曲线L0近似待预测日的归一化曲线。待预测日归一化曲线L0可表示为

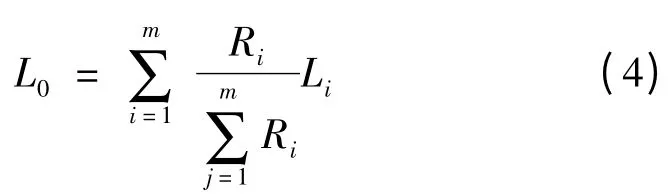
1.4 考虑气象修正的基值预测

归一化曲线以日最大负荷值和日最小负荷值为基础。为了从归一化曲线还原节假日负荷值，需要预测节假日的日最大负荷和日最小负荷。考虑年增长、气象及其他不确定因素，以关联日的日最大负荷和日最小负荷构成基值矩阵，采用指数平滑法消除不确定因素对各年负荷值的影响，并进行灰色关联度气象修正，所得各年平滑值仅反映了负荷的历史增长。最后通过倍比计算，得到节假日的日最大负荷和最小负荷值。具体做法如下:

(1)提取样本数据。从第i 样本集中提取n个节前关联日的日最大负荷和日最小负荷…，n)数据构成2 × n 的输入基值矩阵Ai=，第 0 样 本 集 基 值 矩 阵 记 为 A0=;同样，提取m个同类型日的样本数据构成基值向量

(2)指数平滑计算。进行指数平滑计算，得第i样本集的平滑值向量，记为，计算公式为

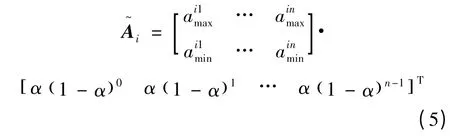
其中α 为逐点基值预测的平滑系数，通常α ∈[ 0.1，0.9 ]。平滑系数确定方法较多，本模型采用0.618 优选法选择平滑系数［20］，在此不做赘述。

(4)利用m个同类型日与待预测日的灰色气象关联度对求出的m个基值分量进行气象加权修正，即

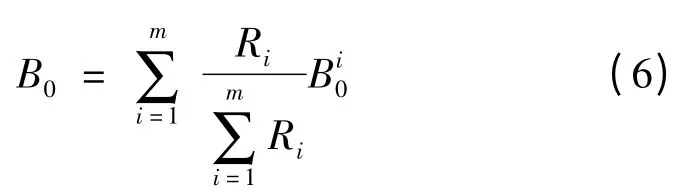
1.5 预测值的还原计算

根据归一化公式，对待预测日的负荷曲线l0进行还原，计算公式为

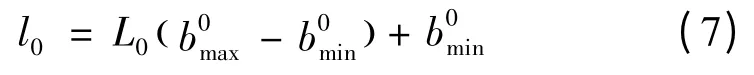
2 预测程序流程图

综合上述模型建立方法，基于日负荷曲线分析的节假日短期负荷预测流程如图4 所示。图中样本年参数m、日参数n 和气象参数r 均根据实际计算样本数据情况而定。由于预测时数据量较大并且计算过程具有重复性，可以使用Matlab 对数据进行处理。

图4 预测程序流程图Fig.4 Flow chart of prediction Method

3 实例分析

以广东省某市2006—2011年每日96 点负荷数据和气象数据为基础，将2011年主要节假日(元旦、春节、五一和国庆)设为待预测日，验证本文预测方法的可行性。

3.1 样本采集与负荷预测

设节前间隔日为5 天，基准日之前的10 天为节前关联日，即n 取10;2011年节前关联日负荷数据构成第0 样本集，2010年节前关联日和同类型日负荷数据构成第1 样本集，以此类推，2006年数据为第5样本集，即m 取5。气象因素向量选取4个分量:日最高气温、日最低气温、日降水量和日相对湿度，即r取4，采集待预测日气象预测数据与5个节前关联日气象数据构成6个气象因素向量。

根据前文所述方法对2011年该市主要节假日进行负荷预测，预测过程如式(1)～(7)所示，计算过程从略。

3.2 预测结果分析

通过本文方法预测2011年该市主要节假日96点负荷曲线。各节假日96 点负荷曲线预测结果的误差统计见表1。计算时取预测值与真实值之差的绝对值，所以表中误差百分值均为正值，统计表反映了预测负荷值相对真实负荷的偏离程度。

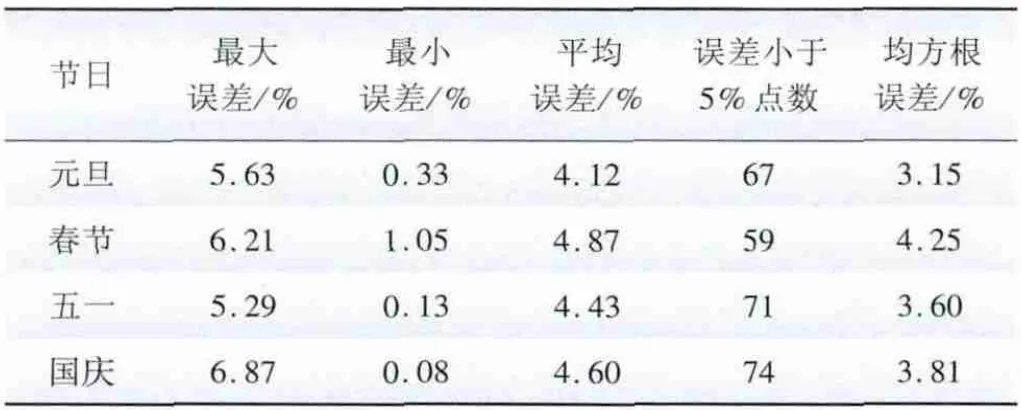
表1 预测结果误差统计表Tab.1 Error statistics of prediction results

结果显示，各节假日96 点负荷预测结果平均误差和均方误差值均小于5%，预测结果令人满意。表中最大误差反映了预测结果偏离真实值的最坏情况，统计表明最大误差均小于7%。

4 结 论

(1)本文提出的节假日负荷预测方法以日96 点负荷曲线预测为目的，考虑日负荷预测的预测间隔时间，符合电力部门实际预测情形，具有较高的实用性。

(2)为了反映同类型日负荷在气象因素影响下的波动性，该法提出基于归一化曲线灰色关联度分析的气象修正预测。该法的气象因素分量选取不受限制，各地区可以根据不同气候特点、预测需求等选取气象分量，具有普遍的适用性。

(3)有别于通常以日最大负荷预测值为基准的处理方法，该法用基于0.618 平滑系数下的指数平滑值为基准，一方面简化了负荷曲线预测过程，另一方面提高了预测结果的精确性。

(4)实证分析表明，该法的预测精度满足要求，是一种行之有效的节假日短期负荷预测方法，可为电力部门节假日负荷预测提供参考。

［1］康重庆，夏清，张伯明． 电力系统负荷预测研究综述与发展方向的探讨［J］． 电力系统自动化，2004，28(17):1-11．

［2］康重庆，夏清，刘梅． 电力系统负荷预测［M］． 北京:中国电力出版社，2007:121-130．

［3］瞿迪庆，陈红敏，吕理想． 模糊线性回归方法在节假日短期负荷预测中的应用［J］． 电力需求侧管理，2013，15(3):16-19．

［4］冯丽，邱家驹． 基于模糊多目标遗传优化算法的节假日电力负荷预测［J］． 中国电机工程学报，2005，25(10):29-34．

［5］Kwang H，Hyoung S，Yong C． Short-term load forecasting for special days in anomalous load conditions using neural networks and fuzzy inference method［J］． IEEE Transactions on Power System，2000，15(2):559-565．

［6］张刚，刘福潮，王维洲，等． 电网短期负荷预测的BP-ANN 方法及应用［J］． 电力建设，2014，35(3):54-58．

［7］李鹏鹏，彭显刚，孟安波，等． 小波贝叶斯神经网络在冲击负荷地区短期负荷预测中的应用［J］． 电力科学与工程，2012，28(11):7-12．

［8］彭显刚，胡松峰，吕大勇． 基于RBF 神经网络的短期负荷预测方法综述［J］． 电力系统保护与控制，2011，39(17):144-147．

［9］刘梦良，刘晓华，高荣． 基于相似日小波支持向量机的短期电力负荷预测［J］． 电工技术学报，2006，21(11):59-64．

［10］成天乐，周胜瑜，李斯，等． 基于极限学习机方法的短期负荷预测［J］． 电力科学与工程，2013，29(4):24-29．

［11］李元诚，方廷健，于尔铿． 短期负荷预测的支持向量机方法研究［J］． 中国电机工程学报，2003，23(6):55-59．

［12］高山，张凌浩，李军红，等． 节假日短期负荷预测的一种实用算法［J］． 江苏电机工程，2002，21(2):19-21．

［13］丁恰，张辉，张君毅，等． 考虑气象信息的节假日负荷预测［J］．电力系统自动化，2005，29(17):93-97．

［14］杨正瓴，田勇，张广涛，等． 相似日短期负荷预测的非线性理论基础与改进［J］． 电网技术，2006，30(6):63-66．

［15］Kspinoza M，Joye C，Belmans R，et al． Short-term load forecasting，profile identification，and customer segmentation:a methodology based on periodic time series［J］． IEEE Transaction on Power Systems，2005，20(3):1622-1630．

［16］姜勇．南京地区春节负荷特性分析及其预测方法［J］． 电网技术，2003，27(5):72-74．

［17］李小燕，文福拴，卢恩，等． 基于相似日负荷修正的台风期间短期负荷预测［J］． 电力系统及其自动化学报，2013，25(3):82-89．

［18］康重庆，周安石，王鹏，等． 短期负荷预测中实时气象因素的影响分析及其处理策略［J］． 电网技术，2006，30(7):5-10．

［19］廖旎焕，胡智宏，马莹莹，等． 电力系统短期负荷预测方法综述［J］． 电力系统保护与控制，2011，39(1):147-152．

［20］叶宗斌，周步祥，林楠，等． 基于等维新息指数平滑法模型的中长期负荷预测［J］． 电力系统保护与控制，2012，40(18):47-51．