不同噪声下几种滤波方法的比较研究及改进*

章浙涛 朱建军 匡翠林 柯宇超

1)中南大学测绘与国土信息工程系，长沙 410083

2)河海大学大禹学院，南京211100

1 引言

GPS 技术已在变形监测领域得到广泛应用，但由于受各种因素影响，GPS 数据中受到不同类型及不同程度噪声的污染，这会对后续数据分析产生不良影响，因此如何消除噪声已经成为一项重要任务［1－7］。

在GPS 变形监测数据中噪声的污染情况千差万别，不同滤波方法在处理不同类型的噪声时效果各有优劣，因此根据GPS 数据所含噪声的污染情况，选取最佳的滤波方法去噪是一个关键问题。由此，本文研究了在不同单一噪声污染下小波滤波、中值滤波以及均值滤波的去噪效果，同时讨论了不同混合噪声污染下几种组合滤波方法的去噪效果。结合三种单一滤波方法，提出了一种改进的组合滤波方法，即先通过频率域的小波滤波，再使用空间域的中值滤波和均值滤波方法。

2 GPS 数据滤波方法

GPS 信号的模型为:

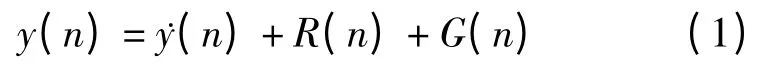
2.1 均值滤波

均值滤波的表达式为［8］:

2.2 中值滤波

中值滤波的数学表示为［9］:

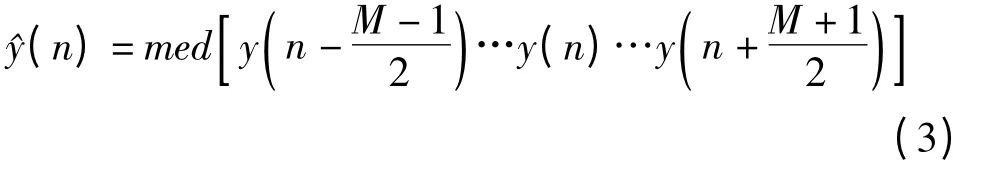
2.3 小波滤波

小波分解及其重构表达式为［10］:

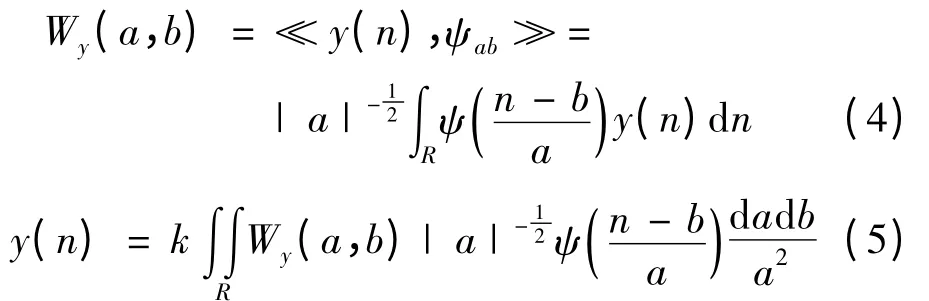
其中，y(n)为观测历元数据，Wy(a，b)为小波分解系数，ψab为小波基函数，a 为伸缩因子，b 为平移因子，＜ ＞为内积，是ψ 的共轭。

2.4 改进的组合滤波方法

改进的组合滤波方法，即利用小波滤波对信号频率域的分离特性，中值滤波对突变信息空间域的检测能力以及均值滤波对信号空间域的平滑性质，通过合理的顺序将这三种方法相结合(图1)。即在进行频率域的小波滤波和空间域的中值滤波方法的基础上，再使用均值滤波方法进行处理。

该方法不但能够有效剔除高频噪声，还具有较强的抵御粗差能力，另外能够保证数据的光滑性，因此是一种较好的组合滤波方法。

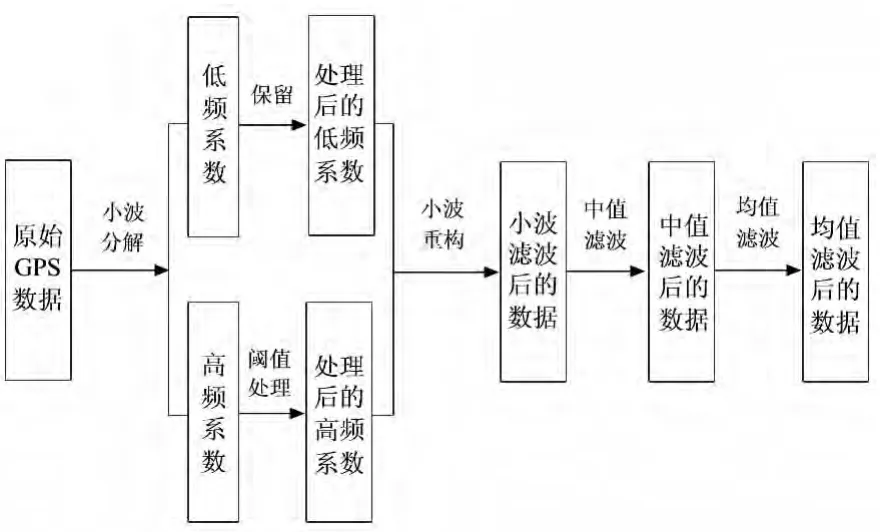
图1 改进的组合滤波方法流程图Fig.1 Flow chart of the improved composite filtering method

3 模拟试验分析

3.1 试验设计

为了比较均值滤波、中值滤波、小波滤波及组合滤波在不同噪声影响下的去噪效果，试验模拟了一组GPS 变形监测数据并加入各种噪声，用不同滤波方法进行处理。模拟变形监测数据如图2 所示，其包含3 个不同周期的正弦信号以及1 个低频趋势信号，信号长度为1 000 个采样点，采样频率为1 Hz。数据模型为:

式中前三项为周期分别是800 s、200 s 以及50 s 的正弦信号，第四项为一个低频趋势信号。为了定量比较去噪效果，选用最为常用的指标信噪比(SNR)作为评判依据［11］，表达式为:

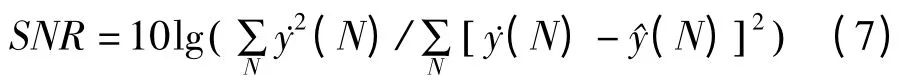
为了保证试验的可靠性，各滤波方法选取最为常用的参数。均值滤波和中值滤波中选用最为通用的5 点均值滤波和5 点中值滤波方法［7］;使用小波滤波时，小波基函数选取具有正交性和高度紧支撑性的db6 小波基，其滤波器长度为12，消失矩为6，根据信号特点将分解层数定为5，采用较好的软阈值处理方法，阈值大小根据启发式阈值准则选取。

图2 模拟的变形监测数据Fig.2 Simulated deformation monitoring data

3.2 单一噪声污染情形

方案一按污染程度由小到大分别加入信噪比为2 ～10 dB 间隔为1 dB 的9 种高斯噪声;方案二按污染程度由小到大分别加入粗差率为0.04 ～0.2 间隔为0.02 的9 种粗差，利用均值滤波、中值滤波及小波滤波进行处理，处理结果如图3。

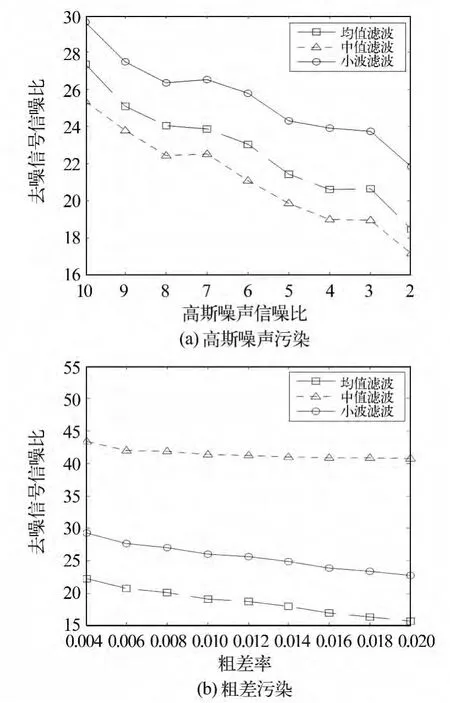
图3 去噪效果Fig.3 De-noising effect

由图3(a)可以发现，三种滤波方法都能对高斯噪声进行有效剔除，其中小波滤波效果最好，均值滤波次之，中值滤波最差;分析图3(b)可知，三种滤波方法同样能对粗差进行剔除，但中值滤波效果远优于其他两种方法，其中小波滤波又好于均值滤波。根据试验和三种滤波方法的原理进行分析，小波滤波、均值滤波在处理高斯噪声时具有更好的效果，小波滤波是从频率域上对高斯噪声进行消除，而均值滤波是在空间域上对高斯噪声进行平滑处理，由于高斯噪声具有高频特性，因此在频率域上消除高斯噪声精度更高;中值滤波则在处理粗差方面具有独特优势，通过排序能够剔除粗差值，而小波滤波经过频率域处理不能准确剔除粗差，只能进行抑制，均值滤波则是将突变信息平摊到周围点上，并没有真正剔除粗差。由此在处理高斯噪声时，偏向于选择小波滤波以及均值滤波方法，处理粗差时则偏向于中值滤波方法。

3.3 混合噪声污染情形

根据实际经验并结合正交试验设计思想，将污染情况分为9 种并加入到模拟数据中，高斯噪声信噪比和粗差率分别为:2/0.02、2/0.012、2/0.004、6/0.02、6/0.012、6/0.004、10/0.02、10/0.012、10/0.004，这9 种情况基本涵盖了实际工程中GPS 数据所含的噪声情况。鉴于单一滤波方法具有各自的局限性，因此考虑组合滤波方法来处理这9 种加噪模拟数据。由于小波滤波和中值滤波分别在处理高斯噪声和粗差时效果较好，因此使用将两者结合的组合滤波方法，采用文献［5］的先中值滤波后小波滤波的方法，文献［6］的先小波滤波后中值滤波的方法，文献［7］的基于高频中值滤波的小波滤波方法，另外还使用了本文的改进方法，同时与均值滤波、中值滤波和小波滤波进行比较研究。其中在2/0.02 的噪声污染水平下，加噪信号与利用改进方法进行去噪得到的信号如图4 所示，可以看到在噪声污染最严重的情况下，依然能够取得非常好的去噪效果。

各滤波方法的去噪效果如表1 所示，同时利用统计学思想，计算各方法去噪信号的平均信噪比见表2。

图4 改进方法的去噪效果Fig.4 De-noising effect of the improved method

根据表1、2 可知，去噪效果最好的是改进的组合滤波方法，证明基于频率域的信息分离结合空间域的粗差剔除和数据平滑，可以起到比较好的去噪效果;三种其他组合滤波方法均不同程度地优于单一滤波方法;总的来说，三种单一滤波方法中，小波去噪效果最好，中值滤波、均值滤波次之;从整体上看，先小波滤波后中值滤波比先中值滤波后小波滤波去噪效果要好，如果先用中值滤波进行处理，容易破坏信号的频谱特性，除非待处理信号粗差率比较高，如在10/0.02 的污染下先中值滤波效果较好，一般来讲优先使用小波滤波再进行中值滤波，只有在高斯噪声污染十分轻微而粗差污染非常严重的情况下才考虑使用先中值滤波后小波滤波的方法;基于高频中值滤波的小波滤波虽然在去噪精度上略差于先小波滤波后中值滤波方法，但是其集中处理高频信息的性质，在一些复杂的观测条件下更能防止破坏原始信息，因此也是一种较为实用的方法。

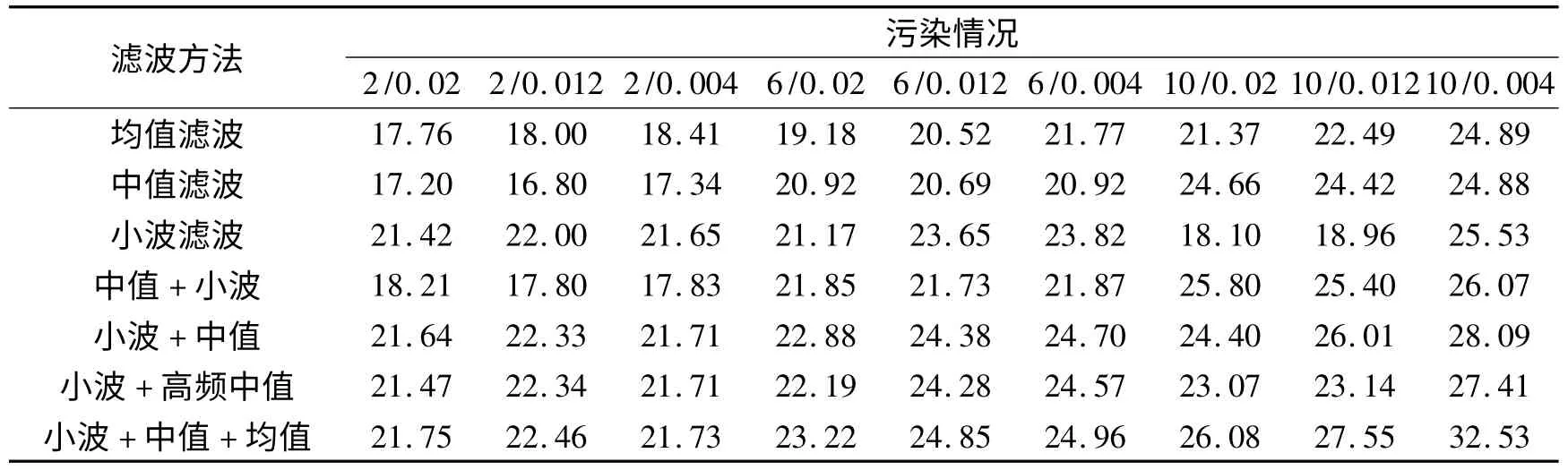
表1 各种方法去噪效果比较Tab.1 Effects comparison of various de－noising methods

表2 各方法的平均信噪比Tab.2 Average signal-to-noise ratio of various methods

5 结论

基于频率域的小波滤波以及空间域的中值滤波和均值滤波方法，可以有效地处理GPS 变形监测数据，在剔除高斯噪声的同时还具有抗粗差性和光滑性，去噪效果优于传统方法，具有良好的工程应用价值。

1 Honglian L，et al.A new GPS dynamic filter algorithm based on stationary wavelet transformation［J］.Future Computer and Communication，2009:270－272.

2 Rao K D and Swamy M N S.New approach for suppression of FM jamming in GPS receivers［J］.Aerospace and Electronic Systems，2006，42(4):1 464－1 474.

3 de Jonge P J ，Bock Y and Bevis M.Epoch-by-epoch positioning and navigation［J］.The Institute of Navigation，2000，8:337－342.

4 黄声享，刘经南.GPS 变形监测系统中消除噪声的一种有效方法［J］.测绘学报，2002，31(2):104－107.(Huang Shengxiang and Liu Jingnan.A novel effective method for reducing noise noises in GPS deformation monitoring system［J］.Acta Geodaetica et Cartographica Sinica，2002，31(2):104－107)

5 史连艳，杨树兴.小波滤波在MR/GPS 制导系统中的应用［J］.数据采集与处理，2007，21(12):165－167.(Shi Lianyan and Yang Shuxing.Application to of wavelet filtering in MR/GPS guidance system［J］.Journal of Data Acquisition ＆Proeessing，2007，21(12):165－167)

6 卞继承.中值滤波和小波变换相结合在信号去噪声中的应用［J］.科技视界，2012，28:292－293.(Bian Jicheng.Application of the method using median Median filter combined with and wavelet transform to de-noisingcombined in the signal to noise［J］.Science ＆ Technology Vision，2012，28:292－293)

7 王坚，高井祥，孙祥中.GPS 单历元形变信号的小波降噪［J］.测绘科学，2004，29(1):24－25.(Wang Jian，Gao Jingxiang and Sun Xiangzhong.Wavelet de-noising of GPS single epoch deformation signals［J］.Science of Surveying and Mapping，2004，29(1):24－25)

8 Hu J，et al.Derivation of 3-D coseismic surface displacement fields for the 2011 Mw 9.0 Tohoku-Oki earthquake from In-SAR and GPS measurements［J］.Geophysical Journal International，2012，11:1－13.

9 Schindhelm C K.Evaluating SLAM approaches for microsoft Kinect［A］.The Eighth International Conference on Wireless and Mobile Communications［C］.IARIA，ICWMC2012:402－407.

10 吴继忠.GPS 观测数据的小波阈值法消噪［J］.大地测量与地球动力学，2009，(4):78－82.(Wu Jizhong.Denoising of GPS data observations with wavelet threshold method［J］.Journal of Geodesy and Geodynamics，2009，(4):78－82)

11 Souza E M and Monico J F G.Wavelet shrinkage:high frequency multipath reduction from GPS relative positioning［J］.GPS Solutions，2004，8(3):152－159.