极地GPS定位中的对流层延迟分析*
许 艳 杨元喜 许国昌
1)长安大学地质工程与测绘学院,西安 710054
2)中国卫星导航定位与应用管理中心,北京 100088
3)地理信息工程国家重点实验室,西安 710054
4)德国地球科学研究中心,波茨坦14473
1 引言
对流层延迟是影响GPS 定位精度的关键因素[1]。对流层延迟的处理方法有对流层模型改正法,引入描述对流层影响的附加待估参数法[2-4]等。在高精度GPS 测量中,由于受模型误差、气象元素测定误差,尤其是气象元素代表性误差的影响,直接建立对流层延迟模型难以取得理想效果。如果将模型求得的值作为近似值,通过较严格的平差计算来估计其精确值是一种较好的方法[5]。
南极地区GNSS 定位具有与内陆地区不同的特性。文献[6]对武汉站和南极地区测站进行对比,发现与中低纬度测站相比,极地定位具有更多的可视卫星,但多数为低高度角。而相关研究表明对流层延迟对低高度角卫星观测的影响较大[7,8]。所以在极地GNSS 定位中需要寻求更有效的改正对流层延迟的方法以提高定位精度。本文分析了利用标准气象元素与实际气象数据计算的对流层改正数的差别,并进行GPS 定位。结果表明,使用实际气象数据模型,在保持同样定位精度的基础上可降低观测数据的截止高度角,即可以利用更多的低高度角的卫星观测信息,提高观测冗余,提高导航定位的精度。
2 对流层延迟改正模型
对流层延迟可表示为:

式中,δ 为对流层总延迟,δdz为天顶方向对流层干分量延迟,Fd为相应的对流层干分量投影函数,δwz为天顶方向对流层湿分量延迟,Fw为相应的对流层湿分量投影函数[3]。
目前,在精密单点定位中常用的对流层模型有Saastamoinen、Hopfield,而投影函数模型有Neill、VMF1、GMF 等[3]。本文中对流层延迟改正使用Saastamoinen 模型和Neill 投影函数模型。
Saastamoinen 模型为[5]:

式中,z 为卫星的天顶角,P是测站大气压,e是水汽压,T是绝对温度,δ 为对流层延迟总量。cosz表示投影函数,可以将其替换为其他的投影函数,本文中将其替换为Neill 投影函数。B 为附加的改正项,是测站高程的列表函数。
在对流层延迟改正模型中要用到测站上的气象元素,实践中一般都使用标准气象元素,即依据海平面上一组标准的气象元素值和测站高程H 求得测站上的气象元素值。
3 对流层延迟改正模型对南极定位精度的影响
3.1 改进的对流层延迟模型
实验数据为2011年2月22日丹麦国家空间中心(DNSC)在南极地区航空重力观测中的地面静态参考站rot1 的数据。数据采样率为1 秒,观测时间为08:40:38—16:53:27,约8 小时12 分钟。
对南极静态参考站rot1 进行PPP 处理时,分别使用标准气象元素法和rot1 站当天的实际气象数据进行对流层延迟改正模型的计算(取截止高度角为15°),得到其对流层延迟改正值分别为δstandard和δreal,以及两种改正值之差δreal-δstandard如表1。

表1 标准气象元素和实际气象数据计算对流层延迟改正值及两者结果之差(单位:m)Tab.1 Tropospheric delays calculated by standard meteorological data and by real meteorological data(unit:m)
从表1 可以看出,分别使用标准气象元素和实际气象数据计算得到的对流层延迟存在明显差别,最大可达0.25 m。通过比较,可以得到两者间的比例因子α 为:

用α 对原对流层改正模型δ 进行处理,得到改进后的对流层改正模型δ'为:

3.2 两种对流层延迟模型对南极定位精度的影响比较
3.2.1 两种模型仅进行对流层模型改正
为了验证比较改进后的对流层模型δ'对定位精度的影响,采用精密单点定位技术对rot1 站数据进行处理时分别使用原对流层模型δ 和改进后的对流层模型δ'。在精密单点定位中,一般是将精密星历和精密卫星钟差代入观测方程,固定卫星轨道和消去卫星钟差项,并且采用双频观测值消除电离层影响,故计算的数学模型为[2]:

式中,c 为真空中光速,Δt 为接收机钟差,δ 为对流层延迟影响,α 为比例因子,εΦ为多路径、观测噪声等未模型化的误差影响,Φ 为消除了电离层影响的组合观测值,υΦ为观测误差,λ 为波长,ρ 为信号发射时刻的卫星位置到信号接收时刻接收机位置之间的几何距离,N 为消除了电离层影响的组合观测值的整周未知数。
对误差方程进行线性化得:

其中P 为观测权矩阵,且

整理可得

当分别使用对流层模型δ 和δ'计算时,其对流层模型误差δ-δ'对定位结果的影响为

在截止高度角取10°和15°时分别使用原对流层模型δ 和改进后的对流层模型的计算结果如表2。
分析表2 可以得到:
1)若采用原对流层模型δ 进行对流层延迟改正,与截止高度角取10°的情况相比,截止高度角取15°时其定位精度在X、Y、Z 方向上分别提高了3.49%、8.76%和1.10%。
2)在截止高度角取15°的情况下,当采用改进后的对流层模型δ'进行对流层改正时,其定位精度与使用原对流层模型δ 结果相比,在X、Y、Z 方向上分别提高了约2.81%、3.03%和2.65%。在截止高度角取10°的情况下,当采用改进后的对流层模型δ'进行对流层改正时,其定位精度与使用原对流层模型δ 结果相比,在X、Y、Z 方向上分别提高了约10.08%、10.60%和10.06%。在截止高度角取5°的情况下,采用改进后的模型δ'进行对流层延迟改正,其定位精度在X、Y、Z 方向上为0.024 6、0.020 6、0.070 9 m,与截止高度角取15°时采用原模型δ 进行对流层延迟改正的定位精度相当。
根据分析可得采用对流层改进模型δ'可以使南极定位在取相同截止高度角的情况下提高定位精度;而在保持同等定位精度的条件下,截止高度角可以从常规的15°降低到5°。

表2 两种对流层改正模型的定位精度(单位:m)Tab.2 Positioning precision calculated by two tropospheric corrected models(unit:m)
3.2.2 两种模型进行对流层模型改正和参数估计
利用模型进行对流层改正后,干分量的部分可以改正90%以上,而湿分量部分的残余影响还比较大[9-12]。因此,在精密定位中,我们一般利用参数估计方法将对流层延迟当作待定参数进行估计求解,而将改正模型所求得的对流层延迟改正视为一种初始近似值。
分别使用对流层模型δ 和改进后的模型δ'进行对流层延迟模型改正,并将该模型改正值当作先验值,再将对流层延迟当作待定参数进行序贯最小二乘[1,13]求解。其处理模型如下:
设观测方程为

相应的误差方程为
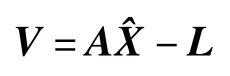
式中,L 为n ×1 阶观测向量,A 为n ×m 阶设计矩阵,Δ 为n×1 阶误差向量,V 为改正数向量,X 为包含对流层参数在内的m×1 阶具有先验统计特性的未知数向量,为估值向量。假设参数验前期望,协方差矩阵QΔ),且观测值独立,L 与独立。依据经典最小二乘(LS)贝叶斯估计原理可得

或

验后协方差阵为

对流层模型误差对参数贝叶斯估式的影响函数为
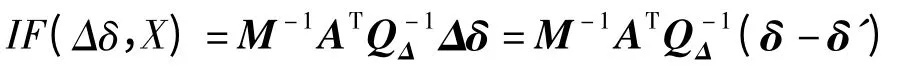
分别将两种模型改正值当作先验值进行参数估计后得到两者的定位结果X、Y、Z 坐标差值结果如表3。
从表3 可以看出,分别将采用模型δ 和改进后的模型δ'计算得到的对流层延迟值作为先验值,再

表3 两种模型对对流层延迟参数联合求解定位结果(单位:m)Tab.3 Comparison of positioning results between models and in co-determination of the tropospheric parameter(unit:m)
进行对流层延迟参数估计求解,得到两者的定位结果X、Y、Z 坐标差值很小,其中X 方向上差值约1 mm,Z 方向上差值约4 mm,Y 方向上基本一致。将两者定位结果取平均值作为标准值,分别与使用模型δ 和改进后的模型δ'进行对流层延迟模型改正后的定位结果见表4。
从表4 可以看出,相对于使用模型δ 进行对流层改正,使用改进后的模型δ'改正对流层延迟,能使定位结果更精确,更接近标准值。

表4 δ 模型和δ'模型改正定位结果与标准值的比较(单位:m)Tab.4 Comparison of positioning results δ and δ' standard values calculated by modelsand(unit:m)
4 结论
1)取相等截止高度角的情况下,使用实际气象数据的对流层延迟改正模型可以提高定位精度。
2)当截止高度角从15°降低为5°时,通过使用实际气象数据的对流层延迟改正模型,两者可以保持基本同等的定位精度,这样就可以利用更多的低高度角的卫星观测,提高观测冗余度。
3)相对于使用标准气象元素进行对流层模型改正,使用实际气象数据改进的对流层模型进行对流层延迟改正,能使定位结果更精确,更接近参考值。因此,对于高精度要求的用户,应该采用实际气象数据进行对流层延迟的改正。
1 戴吾蛟,等.区域精密对流层延迟建模[J].武汉大学学报(信息科学版),2011,36(4):392-396.(Dai Wujiao,et al.Model costructing for regional precise tropospheric delay[J].Geomatics and Information Science of Wuhan University,2011,36(4):392-396)
2 叶世榕,张双成,刘经南.精密单点定位方法估计对流层延迟精度分析[J].武汉大学学报(信息科学版),2008,33(8):788-791.(Ye Shirong,Zhang Shuangcheng and Liu Jingnan.Analysis of the precision for tropospheric delay estimation by precise point positioning[J].Geomatics and Information Science of Wuhan University,2008,33(8):788-791)
3 聂建亮.GPS 精密单点定位算法及故障研究[D].长安大学,2010.(Nie Jianliang.Study on the algorithm and hitch in precise point positioning[D].Changan University,2010)
4 葛茂荣,刘经南.GPS 定位中对流层折射估计研究[J].测绘学报,1996,25(4):285-291.(Ge Maorong and Liu Jingnan.Study on the tropospheric refraction(delay)estimation in global positioning system[J].Acta Geodaetica et Cartographica Sinica,1996,25(4):285-291)
5 李征航,黄劲松.GPS 测量与数据处理[M].武汉:武汉大学出 版 社,2010.(Li Zhenghang and Huang Jingsong.GPS surveying and data processing[M].Wuhan:Wuhan University Press,2010)
6 Xu Yan,Yang Yuanxi and Xu Guochang.Precise determination of GNSS trajectory in the Antarctic airborne kinematic positioning[A].Lecture Notes in Electrical Engineering——China Satellite Navigation Conference 2012 Proceedings[C].2012,159:95-105.
7 佘娣,谢劭峰,彭家頔.卫星高度角变化对大气折射的影响[J].全球定位系统,2011,2:25-28.(She Di,Xie Shaofeng and Peng Jiadi.The influence of satellite elevation angle changing on atmospheric refraction[J].GNSS World of China,2011,2:25-28)
8 任超,等.低高度角卫星信号对提高对流层估计精度的影响分析[J].大地测量与地球动力学,2011,(6):124-127.(Ren Chao,et al.Effects of sign of the low elevation angle GPS satellite on estimation of tropospheric delay[J].Journal of Geodesy and Geodynamics,2011,(6):124-127)
9 Brunner F K and Welsch W M.Effect of the troposphere on GPS measurements[J].GPS World,1993,4(1):42-51.
10 Collins J P and Langley R B.Estimating the residual tropospheric delay for airborne differential GPS positioning[R].ION GPS 1997,Kansas City,1997.
11 Tsujii T,et al.Estimation of residual tropospheric delay for high-altitude vehicles:towards precise positioning of a stratosphere airship[R].ION GPS 2000,Utah,2000.
12 杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.(Yang Yuanxi.Adaptive navigation and kinematic positioning[M].Beijing:Surveying and Mapping Press,2006)
13 Yang Yuanxi.Robust bayesian estimation[J].Bulletin Geodesique,1991,65(03):145-150.

