卫星钟差超短期预报模型分析*

于合理 郝金明 刘伟平 田英国 张 鹤

1)信息工程大学导航与空天目标工程学院，郑州 450052

2)96633 部队，北京100096

1 引言

精密单点定位技术(PPP)由于受制于卫星钟差产品的实时性和精度，其应用主要停留在事后处理模式上。但实时应用才是PPP 的真正优势，如何实时获取高精度的卫星钟差产品是实现该技术的关键［1］。目前，国际地球动力学服务组织(International GNNS Service，IGS)提供的事后精密钟差产品要延迟12 ～18天才能获取，即便是超快速精密钟差也有3 小时的延迟，无法满足实时精密单点定位的需要。IGS 的预报星历产品和广播星历可以满足实时要求，但其纳秒级的精度不能够满足实时要求。

目前美国喷气推进实验室(Jet Propulsion Laboratory，JPL)已经能够以互联网数据流的形式提供时延几秒的精密卫星钟差产品。近几年我国也开始了广域实时精密定位原型系统的研究与建设，高精度卫星钟差的实时获取是该技术实现的关键［2］。但在钟差获取过程中，由于数据解算和网络传输都需要一定的时间，解算的精密钟差产品到达用户时会产生几秒至几十秒的延迟，导致用户并不能真正实时获得当前的精密卫星钟差。因此，对钟差进行超短期的高精度预报对精密单点定位技术的应用有着非常重要的意义。

虽然已经有大量文献探讨过卫星钟差的预报［2－7］，但主要都是中长期预报，即使所谓的短期预报也是研究预报一天左右的钟差，钟差预报精度一般为几个到几十个纳秒，而广域实时精密单点定位系统中所需要的是几十秒内的超短期预报［2］。因此，目前关于钟差预报的研究成果还无法直接应用于实时精密单点定位。为此，本文对超短期高精度钟差预报进行了研究。

2 钟差预报模型

2.1 二次多项式模型

二次多项式模型为:

其中，Δt=ts－t0，Δtsv为ts时刻卫星钟差，a0、a1、a2为二次多项式待估参数，t0表示钟差预报的参考时刻。

当观测数据多于3 个时，利用最小二乘方法建立模型，求解得到模型参数。考虑到模型求解过程中经常会造成法方程矩阵奇异，进而影响卫星钟差预报的可靠性和稳定性，本文采用Givens 变换解最小二乘的方法来估计多项式系数［8］，这种解法无需组成法方程，而是直接通过变换观测方程进行解算，计算效率高且节省内存，在解的精度和数值稳定性都优于通过组法方程的解算方法。

当公式(1)右边后两项为零时则变为

2.2 灰色模型

设原始钟差数据为:

对原始数据x0做一次累加，得对应的新数列为:

其中x1(k)表示一次累加得到新数列x1的第k 个元素，即

对新生成的数列建立微分方程:

建立关于a 和u 的方程为:

a 和u 根据式(7)利用Givens 变换解最小二乘估计求得。将a 和u 代入微分方程(6)，得

由于x1是x0的一次累加序列，灰色模型预报钟差可表述为:

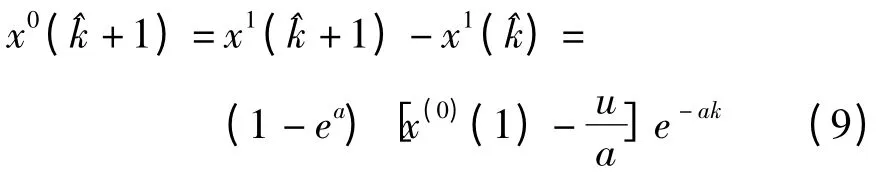
2.3 基于历元间差的二次多项式模型

对原始钟差数据x0作一次差，得

其中，Δx0(k)，k=1，2，…，n表示历元k+1 时刻卫星钟差历元间差值，

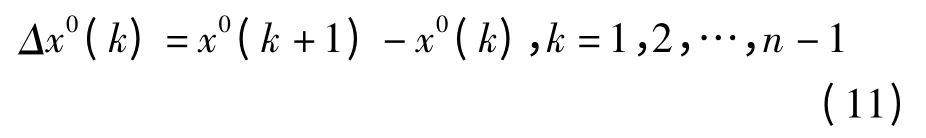
再将历元间作差得到新数列用二次多项式模型预报后续的钟差历元间差，得到钟差历元间差数列:

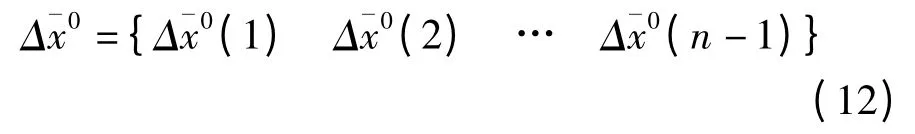
最后再将预报的钟差历元间差结果还原为预报钟差:

3 实验分析

文献［9，10］指出，卫星钟差的预报结果与卫星钟的类型有很大关系。为使实验更具代表性和一般性，根据卫星原子钟类型和卫星编号对照表(表1)，选择不同类型的1、14、17、25 四颗卫星作为实验星进行数据分析。

表1 GPS 卫星原子钟类型和卫星号对照表Tab.1 Atomic clock types of several GPS satellites

研究所采用的试验数据是欧洲定轨中心(The Center for Orbit Determination in Europe，CODE)发布的2012年1月27日cod05 s 的钟差，因为本文所讨论的是卫星钟超短期预报，应当先利用拉格朗日方法内插得到每秒一个历元的钟差数据。实验从当天0 时开始，采用前600 s 的数据求解模型参数预报后续300 s 的数据。

32、28、7、1 四颗卫星运用四种方法预报钟差精度的残差分析图如图1 ～4 所示。纵轴LM、QP、GM、ED 分别表示采用线性模型、二次多项式模式、灰色模型和基于历元间差的二次多项式模型预报结果事后精密钟差的残差曲线。

由图1 ～4 可知，四种方法对不同类型卫星的钟差预报精度大致相同。在5 分钟的预报时间内，32号 卫星误差为－0.06 ～0.3ns，28号卫星误差为－0.20 ～0.15 ns，7 号卫星误差为－0.35 ～0.10 ns，1 号卫星误差为－0.10 ～0.02 ns。

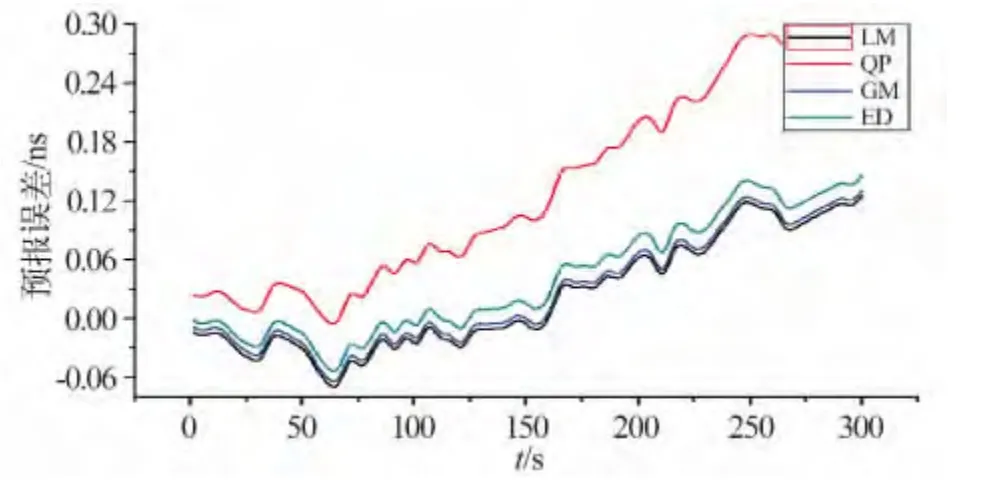
图1 32 号卫星钟差预报残差Fig.1 Residuals of clock error prediction of Sat.32

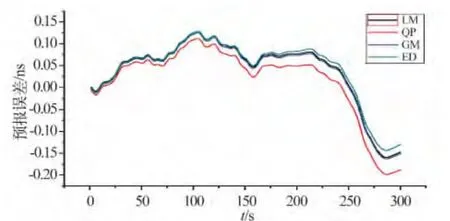
图2 28 号卫星钟差预报残差Fig.2 Residuals of clock error prediction of Sat.28

采用四种模型预报钟差的精度基本相当，且误差残差变化趋势基本一致，证明了四种预报方法的正确性。虽然四种预报方法在长期预报中各有局限性，但对超短期预报而言，四种方法都能达到较高的精度水平。四种方法对不同种类卫星5 分钟的预报精度都能控制在0.36 ns 以内。在更短时间内，卫星钟差几秒、几十秒的预报精度将会更高，能够满足实时精密单点定位的需要。

图3 7 号卫星钟差预报残差Fig.3 Residuals of clock error prediction of Sat.7

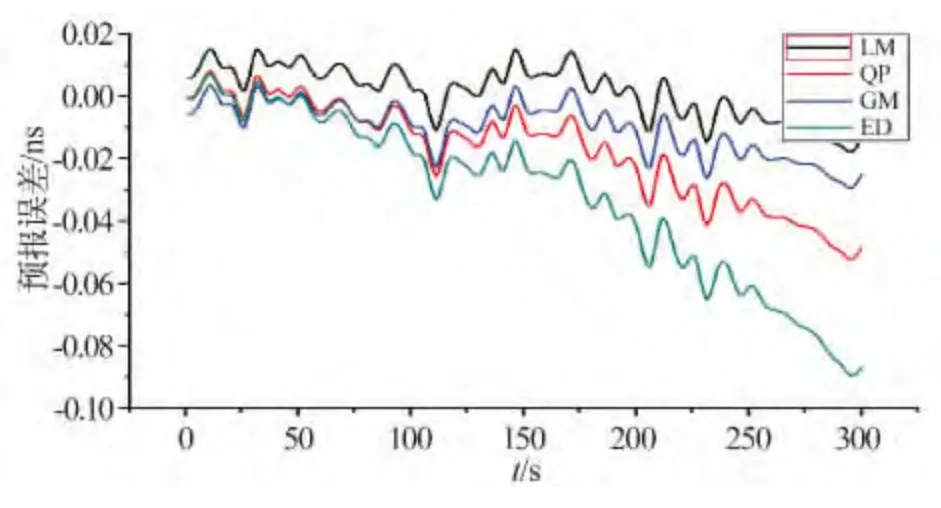
图4 1 号卫星钟差预报残差Fig.4 Residuals of clock error prediction of Sat.1

铷钟较铯钟稳定，在卫星钟差的长期预报或短期预报中一般认为铯钟的预报精度要低于铷钟。但对比图4 和图1、图2、图3 可知，1 号卫星虽为铯钟但预报精度并不比其他卫星钟的预报结果差，在这种小样本的超短期钟差预报中，预报钟差精度与卫星和卫星钟的类型的相关性并不是很大，可能是由于钟差不同时段内的小尺度变化所引起的。为此本文对同一卫星不同时段的结果进行了分析，以1 号卫星为例，采用同一天数据从第5 个小时开始，取前600 s 的数据求解模型参数预报后续300 s 的数据，预报残差结果如图5。

图5 1 号卫星(5 小时)钟差预报残差Fig.5 Residuals of clock error prediction of Sat.1(5 hours)

对比图4、5 可知，同为1 号星同样采用600 s 的数据求解模型参数预报后续300 s 的数据，0 时开始预报的残差为0.1 ns，而5 时开始预报的残差最大值还不到0.04 ns，因此，同一卫星的预报精度与所选取的时段有重要关系。卫星在某一时段的预报精度主要取决于各卫星钟钟差在不同时段内的小尺度变化以及所预报时间的长短。

4 结论

虽然线性模型、二次多项式模型、灰色模型和基于历元间差的二次多项式模型四种卫星钟差预报方法在长期预报钟都存在各自的缺点和局限性，但在超短期预报中精度都很高，都能满足实时精密单点定位的要求，该文也从侧面证明了广域实时精密单点定位系统的可行性。不同种类的卫星，不同的预报方法的预报精度各有不同，但四种方法在超短期预报中整体上精度相当，其预报误差变化趋势也基本一致，并没有哪种方法明显优于其他方法。

在这种小样本的超短期钟差预报中，预报钟差精度与卫星和卫星钟的类型的相关性很小。卫星在某时段的预报精度主要取决于卫星钟钟差在该时段内的小尺度变化以及所预报时间的长短。

致谢感谢全球连续监测评估系统( IGMAS)信息工程大学分析中心对本文工作的支持。

1 阮仁桂.GPS 非差相位精密单点定位研究［D］.信息工程大学测绘学院，2009.(Ruan Rengui.Study on GPS precise point positioning using un-differenced carrier phase［D］.Information Engineering University，2009)

2 宋伟伟.导航卫星实时精密钟差确定及实时精密单点定位理论方法研究［D］.武汉大学，2011.(Song Weiwei.Study on real-time clock offset determination and real-time precise point positioning［D］.WuhanUniversity，2011)

3 刘晓刚，等.几种时间预报模型的钟差长期预报效果分析［J］.测绘通报，2011，1:15－17.(Liu Xiaogang，et al.Analysis of long-term clock bias forecast effects of several time prediction model［J］.Bulletin of Surveying and Mapping，2011，1:15－17)

4 王继刚，等.组合模型预报导航卫星钟差［J］.大地测量与地球动力学，2012，(1):84－88.(Wang Jigang，et al.Combination models of clock error prediction for navigation satellite［J］.Journal of Geodesy and Geodynamics，2012，(1):84－88)

5 Yuan Haibo，et a1.Dynamic grey-autoregressive model of an atomic clock［J］.Metrologia，2008，(6):1－5.

6 李玮，等.灰色系统模型在卫星钟差短期预报中的应用［J］.测绘通报，2009，6:32－35.(Li Wei，et al.Application of grey system model to short-time prediction for satellite clock error［J］.Bulletin of Surveying and Mapping，2008，6:32－35)

7 黄观文，等.GPS 卫星钟差的估计与预报研究［J］.大地测量与地球动力学，2009，(6):118－122.(Huang Guanwen，et al.Study on estimation and prediction of GPS satellite clock error［J］.Journal of Geodesy and Geodynamics，2009，(6):118－122)

8 巍子卿.用Givens 变换解最小二乘问题［J］.测绘工程，1996，5(2):1－7.(Wei Ziqing.Solving the least squares problem with Givens transformation［J］.Engineering of Surveying and Mapping，1996，5(2):1－7)

9 王潜心，等.GPS 卫星钟的特性与预报研究［J］.测绘科学，2010，35(2):36－39.(Wang Qianxin ，et al.Study on GPS satellite clock’s behaviors and prediction［J］.Science of Surveying and Mapping，2010，35(2):36－39)

10 郭海荣.导航卫星原子钟时频特性分析理论与方法研究［D］.信息工程大学，2006.(Guo Hairong.Study on the analysis theories and algorithms of the time and frequency characterization for atomic clocks in navigation satellite［D］.Information Engineering University，2006)