基于卡尔曼滤波的GM(1，1)模型在高铁隧道沉降变形分析中的应用*

文鸿雁 周 吕 韩亚坤 陈冠宇 胡纪元

1)桂林理工大学广西矿冶与环境科学实验中心，桂林 541004

2)桂林理工大学测绘地理信息学院，桂林 541006

3)广西空间信息与测绘重点实验室(桂林理工大学)，桂林541006

1 引言

高速铁路的建设是一个庞大且复杂的系统工程，高铁建设中的隧道建设的难度与精度较其他部分更具挑战性，在隧道的建设过程中需要定期对其进行变形监测，为建设过程提供安全保障。同时，在隧道准备要铺轨时需要评估隧道的沉降变形。

由于隧道本身比较稳定，其沉降变形量小、相对波动较大，加之在对隧道进行沉降变形监测时，受光线、气温、仪器误差等随机因素的影响较大，使沉降曲线出现“小沉降、大波动”现象。针对此现象，本文引入卡尔曼滤波算法，对受噪声干扰较大的沉降监测点进行滤波处理，建立基于卡尔曼滤波的GM(1，1)模型。将新建模型应用于贵广高铁某隧道沉降变形监测点的变形分析与预测中，并与传统GM(1，1)模型进行对比分析，实验结果表明，基于卡尔曼滤波的GM(1，1)模型的综合精度与可靠性均较传统GM(1，1)模型高。

2 卡尔曼滤波

卡尔曼滤波是一种通过对被提取信号有关的观测量的算法估计得出所需信号的滤波方法［1］。离散系统卡尔曼滤波的数学模型由状态方程和观测方程构成，可表示为［2，3］:

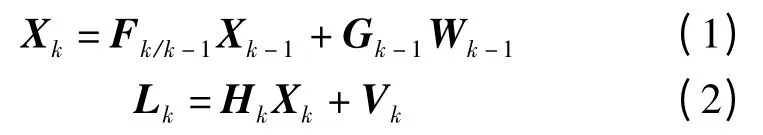
式中，Xk是n×1 阶状态向量，Lk是m ×1 阶观测向量，Fk/k－1是n ×n 阶状态转移矩阵，Gk－1是n ×r 阶动态噪声矩阵，Wk－1是r×1 阶动态噪声，Vk是m ×1 阶观测噪声，Hk是m×n 阶观测矩阵。

根据最小二乘原理，随机离散系统的卡尔曼滤波递推公式为［4－6］:

一步预测值为

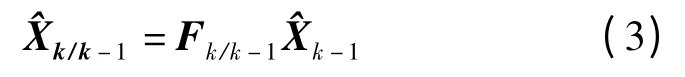
一步预测值的方差矩阵为

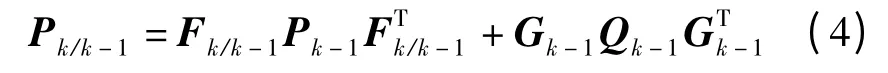
状态向量的估计值为

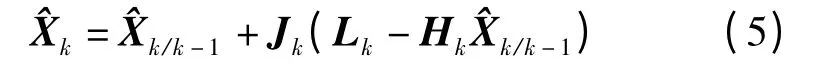
状态向量估计值的方差矩阵为

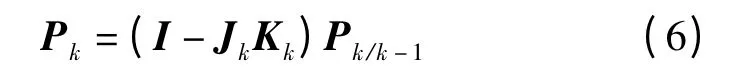
式中，Jk是滤波增益矩阵，为

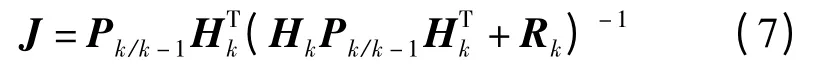
在确定滤波初值后，启动卡尔曼滤波递推算法，依据k 时刻的观测值Lk，递推计算出k 时刻的状态估计值，实现滤波并有效剔除随机干扰噪声的效果。

3 传统灰色GM(1，1)模型

GM(1，1)模型的建立过程为［7－9］:

令x(0)为某监测点的原始序列:

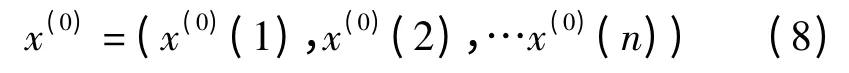
式中，n 为序列长度，k=1，2，…，n。对x(0)进行一次累加生成处理，得到光滑的新生成数列(记x(1)=AGOx(0)):

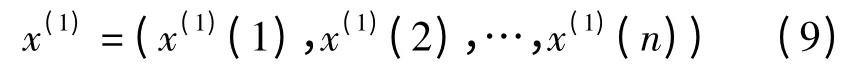
将x(1)进行时间求导，建立GM(1，1)一阶线性灰微分方程:

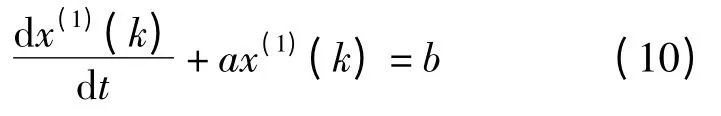
式中，a、b 为待定常数。由文献［7］可知GM(1，1)白化方程的时间响应式为:

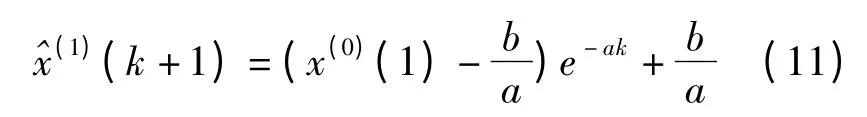
通过累减生成可得GM(1，1)预测模型为:

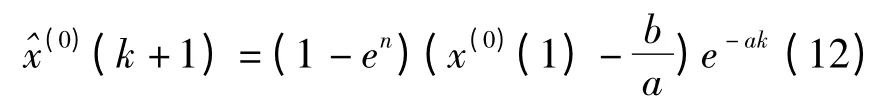
4 模型精度评定

利用后验差检验法［10］评判模型精度。设原始监测数据方差为，残差数据方差为，则计算公式为:

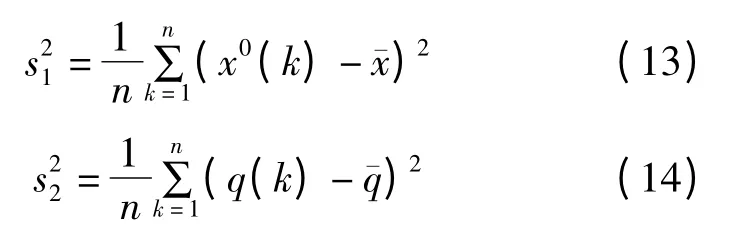
结合C 和P 两项评价指标，对所建模型的精度进行综合评判。各精度等级如表1 所示。

表1 后验差检验法精度等级表Tab.1 Precision grade table of Posterior deviation test

5 实例分析

5.1 卡尔曼滤波去噪

高铁隧道沉降变形监测按照三等沉降变形测量的技术指标进行变形监测，故本文取观测噪声方差Rk=0.5、动态噪声方差Qk=2。本文把监测点的位置与变化速率作为状态参数，由前2 期监测值的平差值可求得滤波初始值:

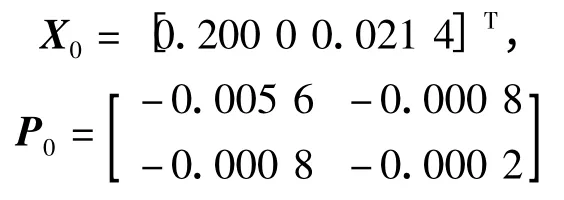
该监测数据序列是隧道沉降变形监测初期的监测值，由于前9 期监测数据在测量时受照明光线影响较大，且监测条件较恶劣，监测数据受随机噪声影响较大，加之该路段隧道地质条件较好，隧道沉降较小，这使隧道沉降变形曲线出现“小沉降、大波动”现象。本文利用上述所得的滤波初始值通过卡尔曼滤波设计程序对该数据进行滤波，对比分析滤波前后数据，结果如图1。

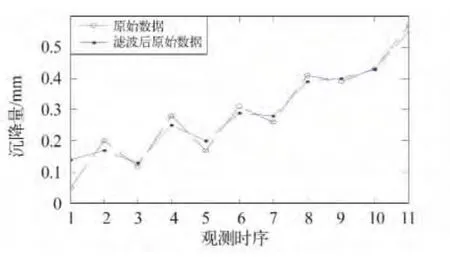
图1 滤波去噪结果与原始数据对比Fig.1 Comparison of denoising results by the Filter

分别计算原始数据与滤波后数据的信噪比得:原始数据的信噪比为6.967，滤波后数据的信噪比为19.633。经过滤波后，数据的信噪比有了较大的提高，说明此次滤波效果较好。

由图1 可知，经过滤波处理之后，原始沉降曲线的波动已减小，经过滤波处理后原始监测数据中的随机噪声的影响得以有效地减弱，沉降曲线更加平滑，更加逼近真实情况。

5.2 建立基于卡尔曼滤波的GM(1，1)模型

以前9 期数据建立基于卡尔曼滤波的GM(1，1)模型，并运用该模型预测第10 期与第11 期的变形量，同时对比分析用原始数据建立的传统GM(1，1)模型的预测结果，对比结果如图2 ～4 所示。

对比分析图2 与图3 可知，经过卡尔曼滤波去噪处理之后，消除了原始沉降监测数据中随机误差的噪声干扰，相对于传统的GM(1，1)模型，基于卡尔曼滤波的GM(1，1)模型的预测值及预测曲线更加逼近真实情况。由图4 可知，基于卡尔曼滤波的GM(1，1)模型的残差曲线波动小于传统的GM(1，1)模型。

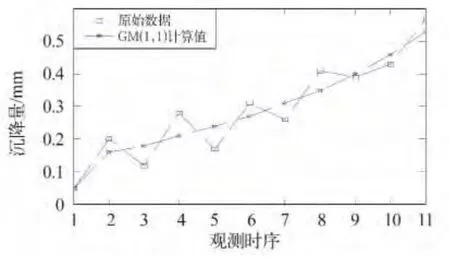
图2 滤波前沉降值与预测值Fig.2 Settlement values before and after filtering with original data

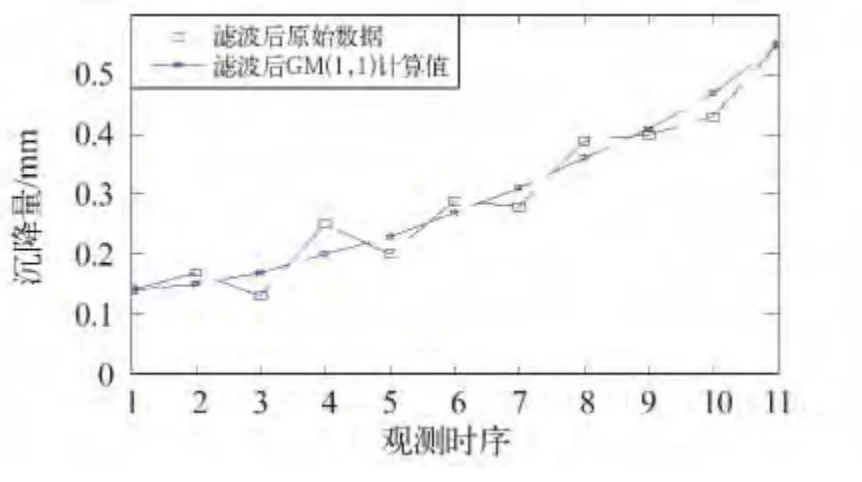
图3 滤波后沉降值与预测值Fig.3 Settlement and predictor after filtering

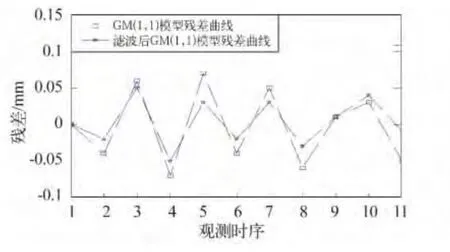
图4 两模型残差曲线对比Fig.4 Comparison of the error curve of the two models

运用后验差检验法评判新建模型与传统GM(1，1)模型的精度，各模型的后验差比值C、小误差概率P 以及模型的综合精度等级，如表2 所示。

利用均方误差、平均绝对误差以及平均绝对相对误差对新建模型与传统GM(1，1)模型进行误差分析得表3。

由表2、3 可知，两个模型均达到了较好的预测精度，但基于卡尔曼滤波的GM(1，1)模型的预测精度更高。

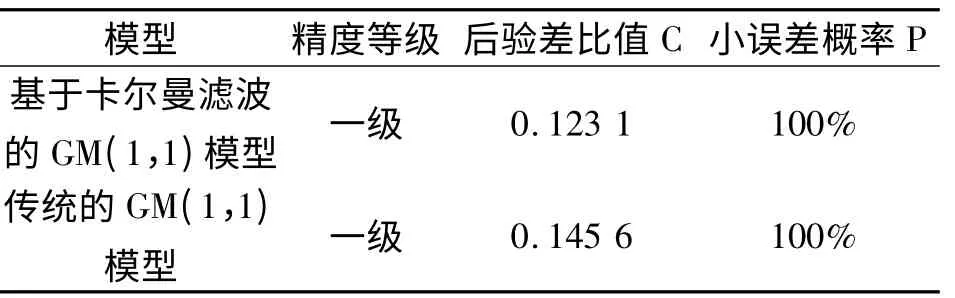
表2 两种模型的精度对比表Tab.2 Comparison of the precision by two models

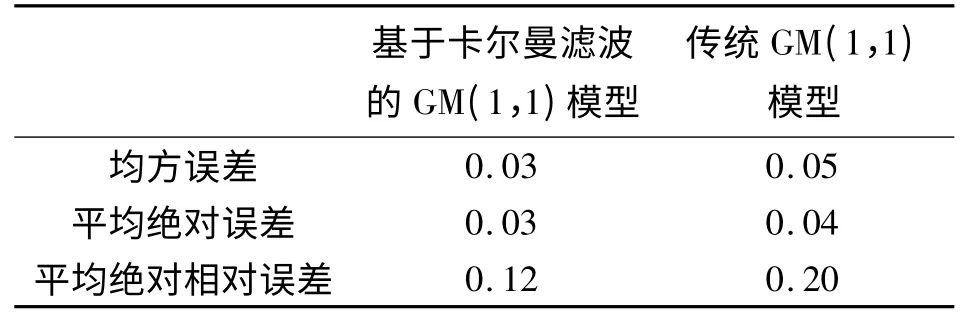
表3 两种模型误差对比表(单位:mm)Tab.3 Comparison of errors by two models(unit:mm)

对各模型的预测曲线进行相关分析，基于卡尔曼滤波的GM(1，1)模型的预测曲线与沉降曲线的相关系数达97%，而传统GM(1，1)模型的预测曲线与沉降曲线的相关系数达94%。对比两个相关系数可知，基于卡尔曼滤波的GM(1，1)模型的线性相关有所提高，因为滤波处理之后，在建模时噪声干扰小，所建模型精度相对于传统GM(1，1)模型更高。

6 结论

针对高铁隧道沉降变形中出现的“小沉降、大波动”现象，在对其进行变形分析时，首先用卡尔曼滤波进行去噪，然后建立基于卡尔曼滤波的GM(1，1)模型进行变形分析。通过工程实例对比分析得出:经过卡尔曼滤波去噪后，可以有效地消除沉降曲线中波动较大的尖端点，使得去噪后的沉降曲线更为合理;滤波后可以有效剔除原始监测数据中的随机误差，在一定程度上提高了GM(1，1)模型的综合精度。

1 张正禄，等.工程的变形监测分析与预报［M］.北京:测绘出版社，2007.(Zhang Zhenglu，et al.Deformation monitoring analysis and prediction for engineering constructions［M］.Beijing:Survey and Mapping Press，2007)

2 马攀，文鸿雁.离散卡尔曼滤波用于GPS 动态变形数据处理［J］.桂林工学院学报，2002，22(3):234－238.(Ma Pan and Wen Hongyan.Application of discrete Kalman filtering to processing of GPS deformation data［J］.Journal of Guilin institute of Technology，2002，22(3):234－238)

3 周吕，文鸿雁，韩亚坤.灰关联Kalman 滤波的大坝变形分析模型［J］.桂林理工大学学报，2013，33(1):95－98.(Zhou Lü，Wen Hongyan and Han Yakun.Research on the model for analizing dam deformation with grey pelational Kalman filter［J］.Journal of Guilin University of Technology，2013，33(1):95－98)

4 余学祥，吕伟才.抗差卡尔曼滤波模型及其在GPS 监测网中的应用［J］.测绘学报，2001，30(1):27－31.(Yu Xuexiang and Lü Weicai.Robust Kalman filtering model and its application to GPS monitoring networks［J］.Acta Geodaetica et Cartographic Sinica，2001，30(1):27－31)

5 韩厚增，王坚，马昌中.基于有色噪声Kalman 滤波的桥梁自振频率提取模型研究［J］.大地测量与地球动力学，2012，(1):123－126.(Han Houzeng，Wang Jian and Ma Changzhong.Study on extracting model of bridge autooscilation frequency based on Kalman filtering with colored noise［J］.Journal of Geodesy and Geodynamics，2012，(1):123－126)

6 何玉晶，杨力，张杰.基于离散系统卡尔曼滤波的电子含量预报分析［J］.大地测量与地球动力学，2011，(5):111－113.(He Yujing，Yang Li and Zhang Jie.Prediction and analysis of ionosphere TEC based on discrete Kalman filter，2011，(5):111－113)

7 邓聚龙.灰色系统基本方法［M］.武汉:华中科技大学出版社，2005.(Deng Julong.The primary methods of grey system theory［M］.Wuhan:Huazhong University of Science and Technology Press，2005)

8 何君，杨国东.灰色预测理论在建筑物沉降中的应用研究［J］.测绘通报，2012，(3):63－64.(He Jun and Yang Guodong.On the application of grey theory to building settlement［J］.Bulletin of Surveying and Mapping，2012，(3):63－64)

9 徐君毅.基于截距修正的GM(1，1)模型在极移预测中的应用［J］.大地测量与地球动力学，2010，(1):88－91.(Xu Junyi.Application of the GM(1，1)model based on intercept correction to polar motion prediction［J］.Journal of Geodesy and Geodynamics，2010，30(1):88－91)

10 周吕，文鸿雁，李超.基于灰色系统与逐步回归及二者组合的大坝变形分析模型研究［J］.城市勘测，2012，(4):135－138.(Zhou Lü，Wen Hongyan and Li Chao.Study on the model for dam deformation analysis based on grey system，gradual regression and their combination［J］.Urban Geotechnical Investigation ＆ Surveying，2012，(4):135－138)