利用卫星测高观测资料反演海浪周期的几种方法比较*
褚永海 罗丹丹 傅 露 倪 清
1)武汉大学测绘学院,武汉 430079
2)武汉大学地球空间环境与大地测量教育部重点实验室,武汉 430079
3)漳州市测绘设计研究院,漳州363001
1 引言
海浪是发生在海洋中的一种波动现象,研究海浪并获取其精确的数据结果是海洋学、气候学非常关注的问题,也是各类海洋工程需要考虑的设计要素[1-7]。描述海浪的主要参数包括有效波高和海浪周期等。其中有效波高(SWH:Significant wave height)是一定时期内的平均高度。当前,国际上常使用的海浪数值模型一般可以直接输出有效波高,卫星雷达测高技术也能直接进行全球海域、全天候、长时期的有效波高观测,但不能直接获取海浪周期信息。1998年以来,文献[8-12]使用高度计观测的风速及有效波高,联合海洋浮标数据,得出了计算海浪平均周期的经验函数及反演海浪周期的方法。但这些经验算法一般都是基于早期测高资料,联合浮标等观测数据及模型数据,通过统计及回归计算,最终获得利用后向散射系数、海面风速及有效波高反演海浪周期的经验函数。所采用的三个信息可以直接从卫星测高数据获取,因此,利用卫星测高观测信息,可以反演全球海浪周期参数。本文详细阐述这些算法,并用较新的JASON1 测高数据进行计算分析,再用ERA-40 模型提供的平均周期进行检核。
2 反演方法
卫星雷达测高技术只能观测得到海浪的有效波高,要得到海浪周期,通常要联合考虑有效波高、海面风速、后向散射截面等参数,目前有许多经验模式函数可以使用。例如,Challenor 及Srokosz 在1991年给出波浪平均周期可以利用海浪谱的零阶矩m0和四阶矩m4计算得到,而零阶矩与有效波高的关系为,四阶矩即为海面均方根斜率,在雷达波垂直入射时,与后向散射截面σ0和海面的Fresnel 反射系数满足关系σ0(0)=,最后得到[7]:

1998年,Hwang 等人[8]利用墨西哥湾地区的浮标数据,结合早期的T/P 数据,基于对海浪的谱峰周期的研究,指出利用海浪平均周期代替海浪的谱峰周期作为海浪的特征周期,可以避免谱峰周期的不稳定性,得到海浪的平均周期为:

Caires 等人[13]2005年利用TOPEX 测高资料和浮标数据,导出的海浪平均周期TZ的经验模型为
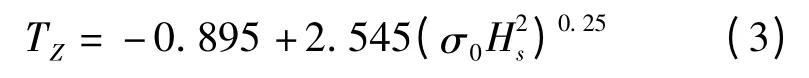
计算结果与雷达目标散射截面σ0和卫星测高观测的有效波高Hs有关。在考虑涌浪存在时,Caires 等人对式(3)进行了改进,提出类似的经验公式[11]:

赵栋梁等[12]于2002年指出自然海况下的波浪满足所谓的3/5 指数率,在已知海上风速U10后,由卫星高度计提供的有效波高可以反演波浪有效周期。为了便于与浮标周期作比较,根据有效周期与平均周期的转化关系,最后得到
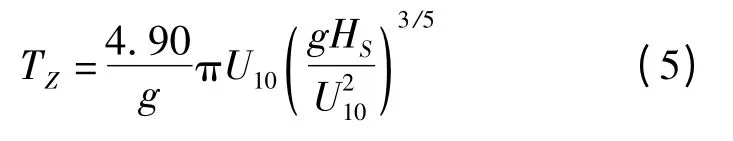
式(1)至(5)中,TZ表示海浪周期,HS为有效波高,σ0为雷达后向散射系数,U10为海面上10 米高处的风速,这三个量均是雷达高度计观测结果。
3 数值结果及分析
3.1 数据
选用JASON-1 卫星测高数据来反演全球海浪平均周期,反演结果利用ERA-40 波浪重分析数据[13]进行检核。其中ERA-40 数据是欧洲中期天气预报中心(ECMWF,European Centre for Medium-Range Weather Forecasts)完成的全球第一份耦合波浪(WAM)和大气环流模式模拟结果并同化观测资料得到的再研究产品。包含有海面大气压、风速、温度、有效波高、平均海浪周期及方向、降雨等55 个海洋环境参数。该资料的范围覆盖全球大部分海域,时间范围从1957-09-01日T00:00—2002-08-31日T18:00 时,空间辨别率为2.5° ×2.5°,时间辨别率为6 小时。ERA-40 重分析资料具有较高精度和时空辨别率,被广泛运用于全球海域特别是北大西洋、北太平洋和南大洋的风浪、涌浪变化特征研究。而JASON-1 任务于2001年7月发射,目的在于延续T/P 任务对全球海面高的观测。为了保持与ERA-40 模型时间一致,本文仅选取了2002年2月(冬季)和7月(夏季)的测高数据,用其反演海浪周期,分析不同反演算法间的差异。
3.2 ERA 40 模型海浪平均周期
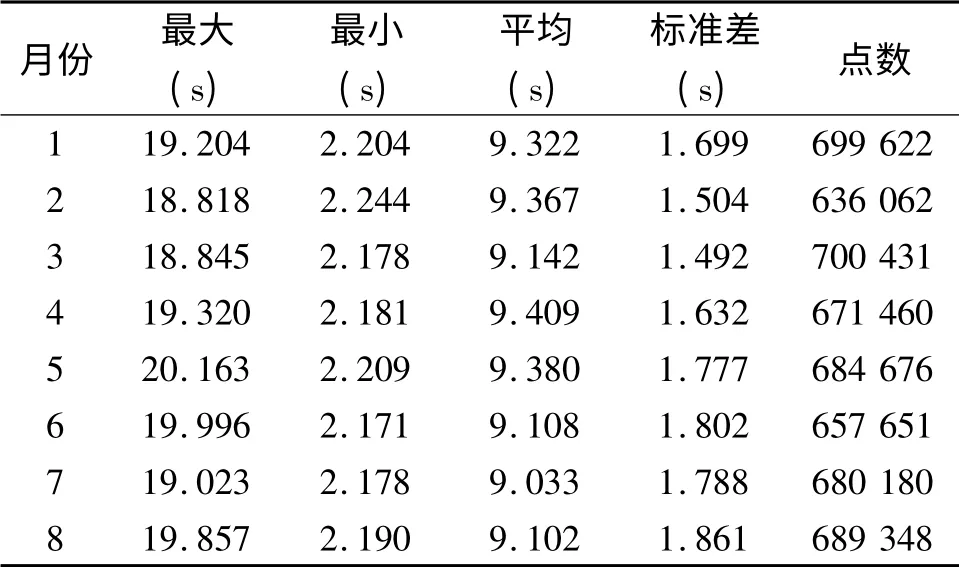
表1 2002年1月至8月ERA-40 海浪周期月平均统计Tab.1 Statistics of monthly mean wave period with ERA-40 during Jan to Aug,2002
表1是ERA-40 气候模型所得2002年1月至8月海域海浪月平均周期统计。表中数据表明,全球海浪的有效平均周期为2.17 s(6月)~20.16 s(5月),平均周期略高于9 秒。
3.3 测高数据反演的海浪平均周期
3.3.1 不同算法结果与ERA40 模型比较
表2 和表3 分别为冬季2月份及夏季7月份的海浪周期差异。
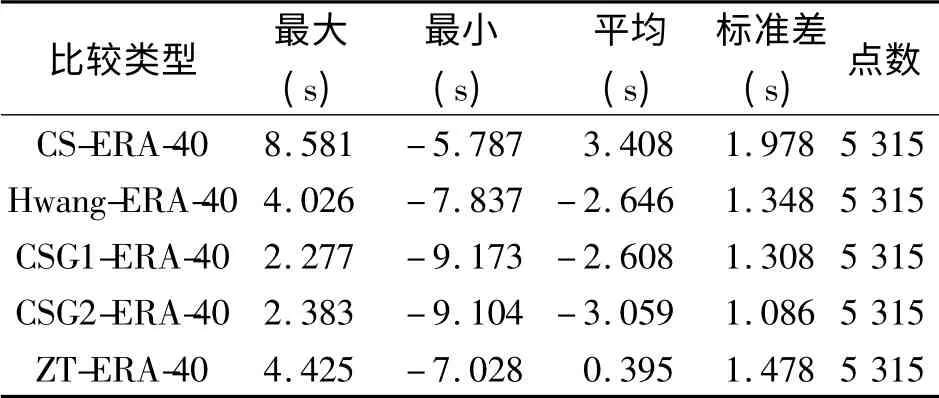
表2 不同算法结果与ERA-40 模型比较(2002年2月)Tab.2 Comparison of the results with different methods to ERA-40 model(Feb,2002)
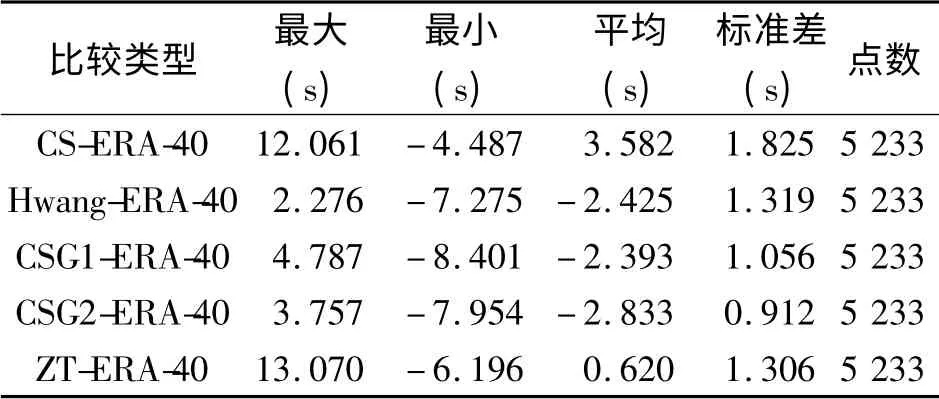
表3 不同算法结果与ERA-40 模型比较(2002年7月)Tab.3 Comparison of the results with different methods to ERA-40 model(Jul,2002)
从表2 和表3 可以看出,单就反演周期与ERA-40 模型提供的平均周期差异的均方差而言,其中CSG2 算法结果最好,与其他4 种方法相比较而言均方差最小,2002年7月的均方差达到0.9 s,而CS算法的均方差最大(2月近达2 s,7月也有1.8 s),效果也最差。CSG1、CSG2、Hwang 算法的反演的平均周期明显要小于ERA-40 浮标观测平均周期,而CS 算法的反演平均周期却明显大于ERA-40 的。从表2、3 还看出CSG1、CSG2、CS、Hwang 四种算法与ERA-40 模型的月平均周期差异都超过2 s,可见他们都有较差的对称性。ZT 法作为解析法,所涉及到的参数均从物理意义上确定,不依赖于观测数据,与所研究的问题无关,是一种普适的方法,所以不受风速高低的影响,其对称性可能比其他几种方法的好。Hwang 法是建立在一系列风浪经验公式之上的,这就意味着这种算法在波浪周期越小越接近风浪的情况下,其反演效果越好,显然Hwang 算法只适合在风浪占优的情况下使用。另外,CSG2是CSG1 的改进公式,在存在涌浪或涌浪占优的情况下应用更合适。从表2、3 中看出CSG2 算法比CSG1算法效果好,可以猜测有可能是因为此处研究涌浪占优的缘故。
3.3.2 JASON-1 海浪月平均周期变化
表4是利用卫星测高数据导出的海浪月平均周期,从表4 可知,其最大平均周期和最小平均周期分别为13.39 s 和0.52 s,月平均周期约为7 s,ERA-40 模型结果(同样只取前8 个月)中与之对应的则分别是20.16 s、2.17 s、9 s。由此看来,由JASON-1高度计应用计算方法CSG2 算法所导出的海浪周期整体上都比ERA-40 模型所得的海浪周期要小,相差约2 秒,该差异与表2 和表3 中的平均差异结果基本一致。
4 结语
针对多种海浪周期反演经验算法,利用较新的JASON1 测高资料分别计算海浪周期,反演结果与ERA-40 模型提供的平均周期进行比较,根据标准差来看,无论冬季还是夏季,CSG2 反演结果与模型相比,精度最好,而CS 算法结果精度最差。Hwang 算法与ZT 算法结果接近。但从平均差异来看,ZT 算法反演结果最接近ERA-40 模型的平均周期。通过各月测高反演的平均周期与ERA-40 模型的月平均周期来看,采用CSG2 方法反演的平均周期比ERA-40 模型的平均周期约低2 秒。
总体而言,CS 算法结果精度最差,其原因主要是其他四种算法在反演中联合使用了浮标观测数据,所得结果接近,而Challenor是从理论方面出发,尚未联合浮标实测资料。因此,要获取更加精确的反演模型,要充分使用各类实测浮标资料及模型资料。
1 金涛勇,等.基于多源卫星测高数据的新一代全球平均海面高模型[J].测绘学报,2011,40(6):723-729.(Jin T,et al.The new generation of global mean sea surface height model based on multi-altimetric data[J].Acta Geodaetica et Cartographica Sinica.2011,40(6):723-729)
2 Andersen O B,Knudsen P and Berry P A M.The DNSC08GRA global marine gravity field from double retracked satellite altimetry[J].J Geodesy.,2010,84:191-199.
3 Sandwell D T and Smith W H F.Retracking ERS-1 altimeter waveforms for optimal gravity field recovery[J].Geophys J Int.,2005,163:79-89.
4 Sandwell D and Smith W H F.Global marine gravity from retracked Geosat and ERS-1 altimetry:Ridge segmentation versus spreading rate[J].J Geophys Res.,2009,114,B01411,doi:10.1029/2008JB006008.
5 褚永海,等.利用测高数据研究南极冰盖高程变化[J].大地测量与地球动力学,2008,(2):67-70.(Chu Yonghai,et al.On height changes of ice sheet over Antarctic from altimetry data[J].Journal of Geodesy and Geodynamics,2008,(2):67-70)
6 褚永海,等.ENVISAT 测高数据波形重跟踪分析研究[J].大地测量与地球动力学,2005,(1):76-80.(Chu Yonghai,et al.Analysis and investigation of waveform retracking data of Envisat[J].Journal of Geodesy and Geodynamics,2005,(1):76-80)
7 Challeor P G and Srokosz M A.Wave study with the radar altimeter[J].Int J Remote Sens.,1991,12:1 671-1 686.
8 Hwang P A,et al.A statistical comparison or wind speed ,wave height,and wave period derived from satellite altimeter and ocean buoys in Gulf Mexico region[J].J Geophys Res.,1998,103(C5):10 451-10 468.
9 Gommenginger C P,et al.Measuring ocean wave period with satellite altimeters:A simple empirical model[J].Geophys Res Lett.,2003,30(22):2150.
10 Caires S and Sterl A.Validation of ocean wind and wave data using triple collocation[J].J Geophys Res.,2003,108(C3):3098.doi:10.1029/2002JC001491.
11 Caires S,Sterl A and Gommenginger C P.Global ocean mean wave period data:Validation and description[J].J Geophys Res.,2005,110(C02003).doi:10.1029/2004JC002631.
12 赵栋梁.自然海况下波浪特征的初步研究[J].青岛海洋大学学报(自然科学版),2002,(32):853-858.(Zhao D.A preliminary study on the characteristics of ocean waves in natural conditions[J].Journal of Ocean University of Qingdao,2002(32):853-858)
13 Uppala S M,et al.The ERA-40 re-analysis[J].Q J R Meteorol Soc.,2005,131:2 961-3 012.

