Z 字形断层系统剪切应变陡降时空分布的数值模拟*

王学滨 马 冰 吕家庆 顾 路

1)辽宁工程技术大学力学与工程学院，阜新 123000

2)中国地震局地质研究所(地震动力学国家重点实验室)，北京100029

1 引言

岩石类材料的微破裂与地震活动具有很大的类似性。目前，在实验室中主要通过声发射技术获取微破裂的时空分布规律，并由此进行断层失稳前兆、地震机理等相关重要问题的探索［1－3］。

数值模拟作为一种研究手段，在破裂失稳研究方面发挥着重要作用。目前的一些数值模拟通过引入非均匀性，模拟破坏单元的数目的演变规律或能量释放的时空分布规律［4－8］，以比拟物理实验中的声发射或天然的微震活动。众所周知，在这些数值模型中，只有破坏的单元才有声发射和释放能量。也就是说，统计发生破坏单元的信息，是一种“一对一”的关系。所谓的“一对一”是指，当一个单元发生破坏时，即输入是1，或者声发射累计数增加1，或者计及这个单元释放的能量，即输出也是1。如果通过研究，能建立一种“一对多”的关系，即输入是1时，输出的是多个单元的信息，那么失稳的前兆可能会更加明显，更易于识别。

本文运用二次开发的FLAC-3D 软件，对含4 条断层的岩石标本进行数值模拟，研究标本内部剪切应变陡降的时空分布规律和两种能量释放的演变规律，以及断层失稳造成的标本整体失稳的前兆及失稳过程。

2 计算模型及参数取值

研究模型高、宽均为0.3 m，被剖分成尺寸相同的9 万个立方体单元，其中断层单元3 312 个。模型中有4 条断层，其中3 条构成Z 字形断层(图1)。断层A、B、C 及D 与水平方向的夹角分别为30°、30°、30°及60°。

首先，在静水压力σ1=σ3=－5 MPa 条件下，对模型进行计算(图1(a))，阻尼力由FLAC-3D自行施加，迭代2 万步后，节点的最大失衡力已经足够小，说明模型已经达到静力平衡状态。然后，在模型的左、右边界施加足够小的、相反的速度v=2.5 ×1010m/时步(图1(b))，即在水平方向上进行准静态拉伸位移控制加载(σ1=－5 MPa)，计算出加载端的平均应力。在FLAC-3D 中，应力为负值代表压缩，反之代表拉伸;σ1≤σ3。一个时步是指一次计算循环，从运动方程经由几何方程，到本构方程，再到运动方程。循环一次，则时步数目增加1。

计算中，断层单元和岩石单元都采用带拉伸截断的应变软化莫尔-库仑模型［6，7］。弹性模量、粘聚力和抗拉强度都服从Weibull 分布;非均质性参数m=9。岩石单元和断层单元的泊松比为0.25 和0.2，弹性模量的均值为55 GPa 和5.1 GPa，粘聚力的均值为37.5 MPa 和5 MPa，抗拉强度的均值为24 MPa 和1.2 MPa，初始内摩擦角为50°和10°，扩容角均取为0°［7］。

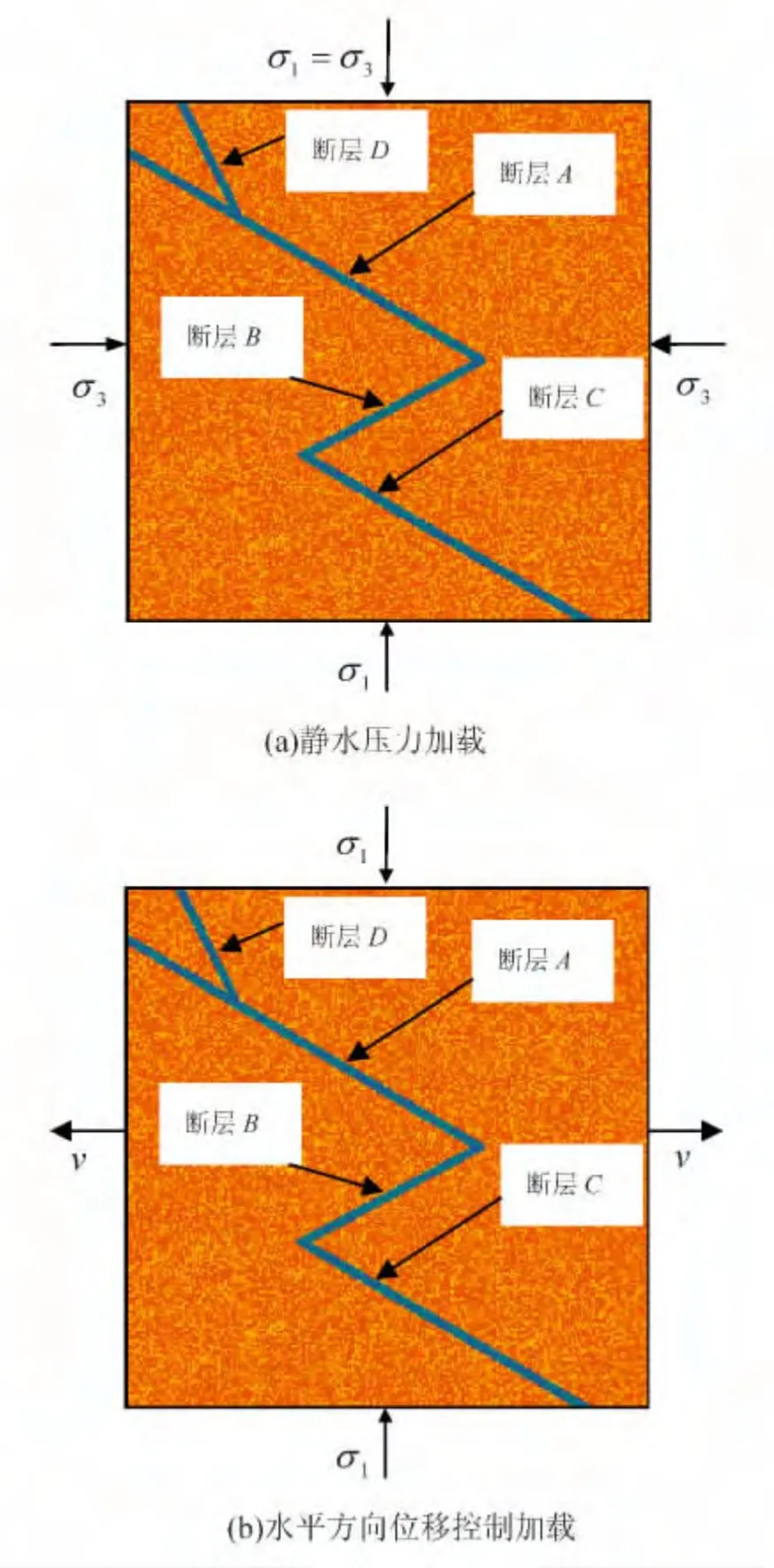
图1 Z 字形断层构造的计算模型Fig.1 A computational model for a Z-shaped fault

3 结果分析

3.1 标本破坏的5 个阶段

图2 平均应力-时步曲线Fig.2 Average stress-timestep curve(a)and average stresstimestep curve in the vicinity of the peak stress(b)

图2 为速度加载端的平均应力随时步的演变规律。由图2可以发现，刚开始时，左、右加载端的平均应力为－5 MPa，稍后，平均应力上升比较快，致使平均应力-时步曲线呈上凸现象，随后，该曲线的斜率趋于定值。

大约7.5 万时步时，平均应力已由负值变为正值，表明标本左、右加载端的平均应力已成为拉应力。继续加载，平均应力-时步曲线开始向下弯曲，即又呈现上凸现象，随后，平均应力达到最高点。然后，平均应力开始下降。当时步达到14 万时，平均应力下降开始变慢，即平均应力-时步曲线越来越平缓，表明标本已接近进入残余变形阶段，残余应力为压应力。这一点似乎是难于理解的。实际上，当水平方向的拉应力降至很低时(接近于零)，标本将在σ1的驱动下在水平方向上运动，标本内部的断层相应地错动，因而标本速度加载端的平均应力可以成为压应力。

总体上，标本的平均应力-时步曲线包括5 个典型阶段:

1)上凸阶段。与位移控制加载有关;

2)直线阶段，即线性稳态阶段［9］。在这一阶段发生位移强化及应力累积;

3)上凸阶段，即偏离线性稳态阶段［9］。预示局部应力开始释放，总体上仍表现为应力累积阶段;

4)软化阶段，为亚失稳阶段和失稳滑动阶段［9］;

5)残余阶段，即调整阶段［9］。

图2(b)为应力峰及附近放大结果。由图2(b)可见，在应力峰之前，平均应力呈非线性上升特点，但有许多应力降，应力降的幅度比应力峰之后的小。

图2(b)中，带箭头的虚线为平均应力突然下降的时刻，该时刻标志着标本整体失稳的开始，标本整体失稳是断层失稳错动造成的。

在应力峰至标本失稳开始时刻之间，总体上平均应力是下降的，但存在局部的上升和下降，应力降尽管比应力峰之前的大，但远小于标本整体失稳之后的应力降。这一阶段应对应于地震的短临阶段或亚失稳阶段［9］。观察短临阶段平均应力的变化规律可以发现，在大约前2/3 阶段(亚失稳Ⅰ阶段)，应力降的幅度不太大，尽管应力释放，但并不占优;在后1/3 阶段(亚失稳Ⅱ阶段)，存在较大的应力降，表明应力释放开始占优势。

3.2 剪切应变陡降的时空分布规律

在8 ～22 万时步共划分70 个时段，每个时段持续2 000 个时步。图3 为剪切应变陡降量在不同时段的分布规律，本文仅统计超过5 ×10－6的剪切应变降(或称之为剪切应变陡降)。为了与上述结果进行对比，图4 给出了拉伸应变能及剪切应变能释放［6，7］的时空分布规律。限于篇幅，仅给出了有代表性的部分时段的结果。

第1 ～13 时段(图3(a，b))，剪切应变陡降量较小，零星地分布在除断层A 上靠近标本左端面的局部区段外的各条断层上。在第1 时段时，标本所受的平均应力尚处于线性阶段，在第13 时段时，平均应力早已进入非线性阶段，即应力峰之前的上凸阶段。

第15 ～19 时段(图3(c ～e))，剪切应变陡降量明显增大，主要集中在断层A、C 上，特别是在断层A与D 相交汇的位置。显然，断层A 与D 形成了一种拐折结构。拐折部位的破坏为其他部位的破坏创造了条件。由图4(a)可以发现，在断层A 上有一个单元释放了较高的拉伸应变能;此外，在拐折部位可以发现一些单元释放能量。在第19 时段时，标本所受平均应力已接近应力峰。

第21 时段(图3(f))，标本的平均应力已处于应力峰附近，许多发生剪切应变陡降的单元云集于断层A 与D 的拐折部位，这一位置即将完全破坏。

第23 时段(图3(g))，标本的平均应力已处于短临阶段。此阶段观察到的各种现象应与标本整体失稳的前兆有关。发生剪切应变陡降的单元已发生在断层B 上，这是此前少见的现象。中间断层B 的破坏或错动，导致了标本的整体失稳。由图4(b)可以发现，在断层C 上有一个单元释放了非常高的剪切应变能;此外，在拐折部位和中间断层B 上，都可以发现大量的单元释放能量。

第25 ～29 时段(图3(h ～j))，标本的平均应力已处于应力峰之后，剪切应变陡降比较密集地分布在各条断层附近，这意味着各条断层上的高强度单元被相继错断，造成了标本整体的失稳。由图4(c)可以发现，能量释放遍布在各条断层上。

第31 ～63 时段(图3(k，l))，发生剪切应变陡降的单元变少，回归平静，零星地散布在各条断层上，标本的平均应力处于缓慢的下降阶段，随着变形的继续，逐渐进入残余阶段。能量释放继续发生(图4(d))。

3.3 3 种量的统计结果分析

图5是对释放的剪切应变陡降、拉伸应变能及剪切应变能统计结果，分别统计这些量的累计(在任一时段之内，将所有单元的某种量求和)、最大值及发生剪切应变陡降或能量释放的单元数目。在图5(b，e，h)中，可以观察到上述3 种量的最大值随时段的演变规律。

图3 不同时段内剪切应变陡降的时空分布(圆圈的半径代表剪切应变陡降的大小，圆圈的中心标明了发生剪切应变陡降的单元位置)Fig.3 Spatiotemporal distribution of the shear strain with steep drop in different timestep intervals

图4 不同时段弹性应变能释放的时空分布(圆圈的半径代表两种能量释放的大小，圆圈的中心标明为能量释放单元的位置;黑色和红色圆圈的半径分别代表发生剪切和拉伸破坏单元能量释放的大小)Fig.4 Spatiotemporal distribution of the liberated elastic strain energy in different timestep intervals

第1 ～13 时段，由图5(a ～c)可以发现，与剪切陡降有关的3 种量随着时段的增加，并无大的变化。但是，在与拉伸应变能及剪切应变能释放有关的一些量上，却能发现增加的现象(图5(d ～g，i))。在图5(h)中，发生拉破坏单元能量释放的最大值处于较高的水平上，这应该与断层单元的强度比岩石单元的低，先发生拉张破坏有关。

第15 ～19 时段，随着时段的增加，很多量都在增加(图5(a ～g，i))。图5(h)的结果是个例外，在第18 ～19 时段内，发生拉张破坏单元能量释放的最大值下降到较低的水平，表现为异常的平静，尽管此时发生拉张破坏单元的数目及它们能量释放的累计并不小。这说明，尽管事件比较多，但没有大事件。

第21 时段，图5(h)中的结果继续表现为低值。

第23 时段，图5(a，c ～f)可以观察到与剪切应变陡降及能量释放有关的量的加速现象;图5(h)中，结果仍然处于低值;图5(i)中，结果已经由上凸拐至水平。

图5 9 种力学指标在70 个时段中的表现(虚线标明了标本整体失稳的开始)Fig.5 Evolution of nine mechanical parameters during 70 timestep intervals(The dashed line denotes the onset of the overall instability of the sample)

第25 ～29 时段，图5(a ～c)中的3 个结果都表现为高值，特别是在图5(a，c)中，两种结果表现为全局的最高值。在图5(d，e，g)中，各种结果也都表现为高值;在图5(d，f，g)中，随着时段的增加，各种结果上升的趋势比较明显，这与图5(i)中结果的表现正好相反;在图5(h)中，结果从低值有所恢复。从图5(d，f，g，i)可以发现，第25 ～29 时段的结果在此前和此后的结果之间起到过渡的作用，即经过25 ～29 时段，各种结果从一种规律转变成另一种规律，这反映了标本变形模式的转变。

第31 ～63 时段，图5(a，c)中的两种结果降到比第1 时段还低的程度;图5(d)中，结果在高水平上波动;图5(f)中，结果不断增加;图5(g)中，结果与图5(d)中的结果具有一定的类似性;图5(e ～h)中，每种结果存在一定的波动，但小于全局的最大值;在图5(i)中，结果维持不变。

总之，从一些与剪切应变陡降和能量释放有关的结果的演变规律上看，在第25 时段稍前，能看到有的加速，有的拐平，有的处于低谷等异常，这说明标本整体失稳的前兆是有的，但表现各异，明显程度也不相同。似乎，一些与剪切应变陡降有关的量具备一定的优势，因为在失稳稍前及失稳过程中(加载端平均应力快速下降)，它们都处于高值，远高于此前及此后的背景值。这有利于准确识别标本所处的应力状态和整体失稳的时刻。

4 结论

1)对于由4 条断层构成的Z 字形断层系统，断层A 与D 形成了拐折断层，拐折部位的破坏及错动为其他断层的破坏及错动创造了条件，两条平行断层A 与C 之间的断层B 的破坏及错动造成了标本整体的失稳。

2)在标本整体失稳稍前，能观察到一些与剪切应变陡降和能量释放有关的量发生了异常的变化，例如，加速、拐平及处于低谷。与剪切应变陡降有关的两种量在标本整体失稳稍前及应力急剧下降过程中，处于高值，显著地区别于此前及此后的低背景值。

3)与剪切应变陡降有关的一些量在失稳过程中表现突出的原因是由于一个发生破坏的单元，能引起其周围大量未破坏单元的反应，因而更有利于断层失稳前兆的识别，相当于对前兆起到了放大的作用。

4)本文的数值模拟研究是初步的，尚有许多问题值得探讨，例如，不同的断层系统在失稳过程中，一些与剪切应变陡降有关的量是否存在共性和差异;各条断层的失稳是否也能通过剪切应变陡降反映出来;亚失稳阶段的仔细考察，等等。

致谢衷心感谢导师马瑾院士的指导!

1 来兴平，等.基于AE 的煤岩破裂与动态失稳特征实验及综合分析［J］.西安科技大学学报，2006，26(3):289－292，305.(Lai Xingping，et al.Comprehensive characteristics analysis of crack propagation and dynamical destabilization of coal-rock based on acoustic emission experiment［J］.Journal of Xi’an University of Science and Technology，2006，26(3):289－292，305)

2 李争荣，等.岩体失稳过程中的声发射监测研究［J］.金属矿山，2012，(1):28－32.(Li Zhengrong，et al.Study on AE monitoring for rockmass failure processing［J］.Metal Mine，2012，(1):28－32)

3 马胜利，等.断层阶区对滑动行为影响的实验研究［J］.中国科学D 辑:地球科学，2008，38(7):842－851.(Ma Shengli，et al.Effect of fault jogs on frictional behavior:An experimental study［J］.Science in China(Ser D)，2008，38(7):842－851)

4 Liu H Y，et al.Numerical studies on the failure process and associated microseismicity in rock under triaxial compression［J］.Tectonophysics，2004，384:149－174.

5 Fang Z and Harrison J P.Development of a local degradation approach to the modeling of brittle fracture in heterogeneous rocks［J］.Int J Rock Mech.Min.Sci.，2002，39(4):443－457.

6 Wang X B，Ma J and Liu L Q.Numerical simulation of failed zone propagation process and anomalies related to the released energy during a compressive jog intersection［J］.J Mech Mat Struct.，2010，5:1 007－1 022.

7 Wang X B，Ma J and Liu L Q.A comparison of mechanical behavior and frequency-energy relations for two kinds of echelon fault structures through numerical simulation［J］.Pure Appl Geophys，2012，169:1 927－1 945.

8 王学滨.缺陷数目对岩样声发射及应变能降低的影响［J］.中国有色金属学报，2008，18(8):1 541－1 549.(Wang Xuebin.Influence of imperfection number on acoustic emissions and elastic strain energy decrease of rock specimens with initially random imperfections［J］.The Chinese Journal of Nonferrous Metals，2008，18(8):1 541－1 549)

9 马瑾.地震新主体地区和失稳危险阶段的探寻［J］.世界地震动态，2012，(6):231.(Ma Jin.Study on the new seismic major region and hazardously unstable steps［J］.Recent Development in World Seismology，2012，(6):231)