多足机器人足端支反力求解方法比较
赵士杰 郭祖华
(北京航空航天大学,北京,100191)
多足机器人足端支反力求解方法比较
赵士杰 郭祖华
(北京航空航天大学,北京,100191)
多足移动机器人运动过程中足端支反力的求解是一个难题,本文介绍并比较了两种计算方法,即伪逆法和优化方法。伪逆法将等式约束线性化处理并补充到平衡方程中,然后利用伪逆理论求解;优化方法则以各个关节力矩的平方和最小为目标函数,搜寻最优解。本文用伪逆法、基于常规规划理论的优化方法和遗传算法分别实现了某6足机器人足端反力的求解。通过对计算结果进行分析比较,得知:伪逆法效率高,但结果偏于保守,机器人行走时能耗偏高;优化方法得到的结果虽然使机器人行走时能耗更少,但计算速度慢,无法用于实时控制。
多足机器人,动力学,足端力分配
0 引言
多足移动机器人是一种特殊的移动机器人,其仿生的移动模式使得人们对该类机器人的研究方兴未艾。多足机器人处于准静态状态下,至少有三条腿支撑才能保持机体稳定,而机器人三足支撑时,将有9足端反力。对于一个移动机器人而言,只能列出与足端反力相关的6个平衡方程,这就导致多足机器人足端反力的求解是一个多解问题。而实际机器人行走的某时刻只有一组唯一的足端反力(或关节力矩)存在,所以在多组解中只有一组解与实际行走状态是相符的。本文比较和分析现有方法的特点,为在仿真和控制过程中机器人足端反力和关节力矩求解方法的选取提供参考依据。
国内外多位学者对以上问题进行了研究,提出了不同的解决方法。文献[1]采用螺旋理论列出了多肢体系统的平衡方程,并根据伪逆方法的思想,推导了足端支反力的求解公式,但该方法没有考虑摩擦约束。
文献[2]提出用对偶线性规划算法(Compact-Dual Linear-Programming,CDLP)解决力分布问题,对偶线性规划算法是线性规划算法中的一种,首先求解出线性约束等式的一般解,然后把线性约束等式的一般解代入目标函数和不等式约束中,以消除线性等式约束,减小计算量,再利用对偶原理把约束的个数转化为变量的个数,最后,利用单纯形法寻找最优解,但是该方法容易产生解不连续的问题。
文献[3]以电机所需功率总和最小为目标函数,将非线性不等式摩擦约束简化为线性等式和不等式方程,消除线性约束,减小计算量,最后用优化算法求解各足端反力。本文虽然采用非线性规划算法克服了解不连续性问题,但和其他优化方法一样存在计算效率低的问题,不能用于实时控制。
文献[4]补充了三个与足端反力有关的线性方程,与力/力矩平衡方程组成一个有唯一解的线性方程组,实现了解析求解,计算速度快,但忽略了一些约束条件,得到的关节力矩较大。
文献[5]中J.F.Gardner也采用了伪逆法,但他根据实验的结果补充了两个摩擦力约束方程,对摩擦力方程进行线性化处理后加入到原来的力平衡方程组中。
文献[6]中Mustafa Suphi Erden采用了优化方法直接求解机器人足端支反力,作者由机器人动力学方程求解关节力矩,考虑足端的摩擦约束,以关节力矩平方和最小为目标函数,进行优化求解,这种方法使得机器人关节力矩达到最小。
综上所述,求解多足机器人足端反力的方法有两类,一类是伪逆法,另一类是优化方法。本文以六足机器人为例,在给定的机器人运动形式下,分别采用这两种方法对足端反力和对应的关节力矩进行求解,针对第二种方法,本文采用经典的数学规划算法和遗传算法对优化模型进行求解,最后对结果进行了比较分析。
1 机器人模型及动力学建模
六足机器人是一个复杂的机械系统,它是由躯体和绕躯体均匀分布的六条腿构成。每条腿有3个连杆,通过3个转动关节连接起来,有3个自由度,机器人模型中包含19个刚体,共有24个自由度。本文所使用的六足机器人模型如图1所示,机器人的主要结构和质量参数见表1。
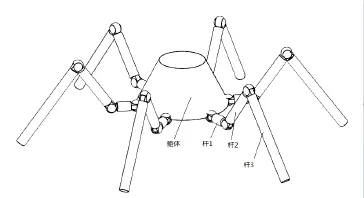
图1 六足机器人模型
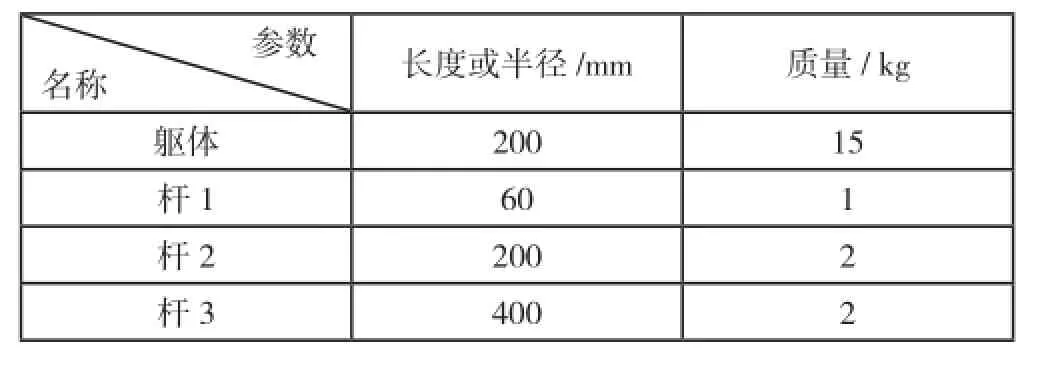
表1 六足机器人躯体及杆件的设计参数
采用D-H方法建立各个刚体的坐标系,利用Newton-Euler公式建立六足机器人的动力学模型,消去动力学方程中的内力或直接运用达朗伯原理可以列出机器人运动过程中某时刻的平衡方程(1):
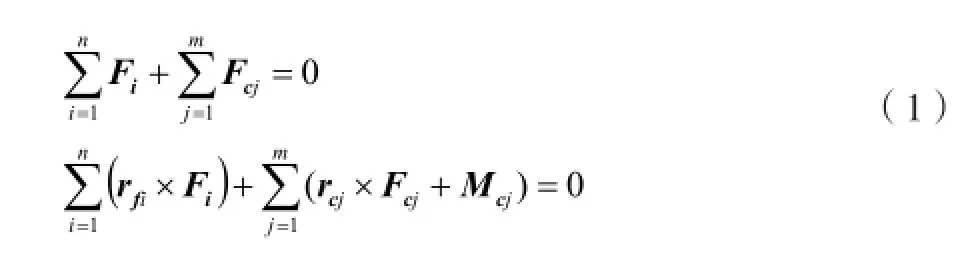
以上公式中所有的量均在惯性坐标系下表示。
把方程(1)写成矩阵形式:

其中:
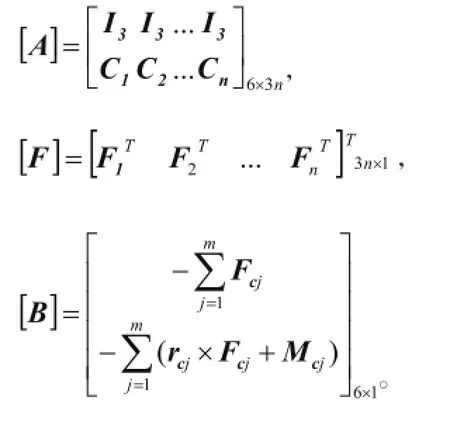
为了便于表达机器人的打滑条件,定义机器人足端力的切向分量和法向分量的比值(简称为切法比系数)如下:
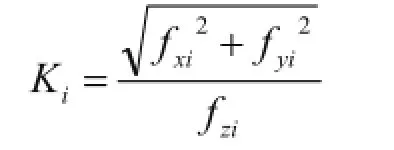
显然,为了避免机器人打滑,足端力的各个分量必须满足如下约束条件:

其中μ为足端与地面的滑动摩擦系数。
对六足机器人而言,至少有三条腿支撑才能保持稳定,即。方程(2)中未知量的个数大于方程的个数,足端支反力的可行解不唯一。该类方程可以采用优化方法来求解,即求解满足某一特定目标的最优解。现主要有两种思路:一是用伪逆法求解方程(2),二是以关节力矩的平方和最小为目标函数,用各种优化算法迭代求解。本文考察六足机器人3条腿支撑时的平衡方程,其中仅有6个方程,但有9个未知量。
2 伪逆方法
利用伪逆方法求解足端反力本质上是求解一个含有等式约束的二次规划问题,显然伪逆求解方法中没有办法计入(3)式所表示的非线性不等式约束。根据文献[5]中Gardner研究的结论,引入两个等式约束方程。
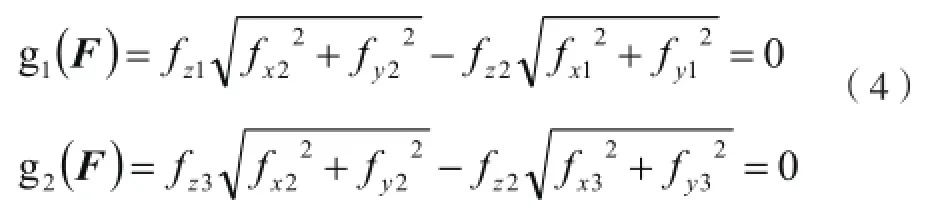
方程(4)保证了各个足端支反力fF的法向力F0和切向力的比值相等。我们可以这样认为:真实准确的足端支反力是支反力初始值和偏差FP量的和。故有:

对于非线性约束方程(4),我们利用泰勒公式在支反力初始值F0处进行一阶近似,得:
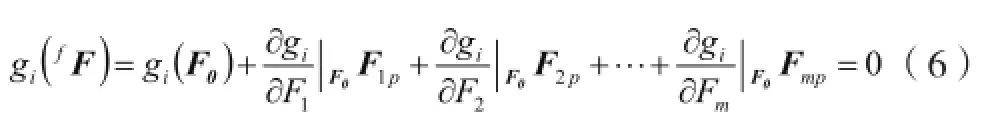
利用方程(4)(5)(6)可得:

其中:
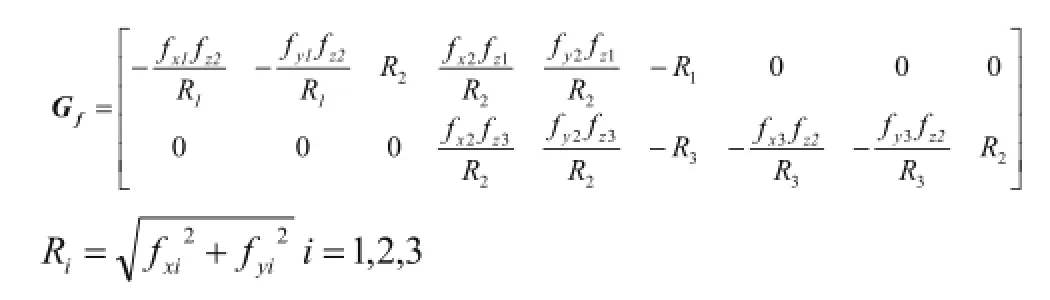
把方程(5)和方程(7)代入方程(2)中,形成新的方程组(8)。

简记作:

3 优化方法
足端支反力的求解也可以直接采用非线性优化的方法,优化时一般以机器人行走过程中关节力矩最小为目标。机器人在行走时,其运动状态和所受的外力必须满足机器人的动力学方程,于是,可以采用如下优化模型来求解机器人的足端支反力。

4 计算结果及分析
现只考虑机器人行走一步的情况,机器人的躯体质心轨迹和迈步足的足端轨迹按照六次多项式给出,分别采用伪逆方法、遗传算法和传统优化方法对该问题进行求解。编程工具为Matlab,遗传算法使用Matlab中的函数GA,传统的优化算法采用Matlab优化工具箱的函数fmincon。在Matlab中仿真了六足机器人迈一步的动作,各种方法实现一次足端支反力的求解所花费的时间分别为:利用伪逆法求解所需时间为0.0241s,利用Matlab工具箱fmincon函数所需时间为5.1037s,而利用遗传算法求解所需时间为5282s。
可见,利用伪逆法求解足端支反力所需要的时间很小,可以用于实时控制,而优化方法耗时长,无法用于实时控制。在两种优化方法中,传统优化方法(fmincon)需要的时间相对较少,而遗传算法求解运行时间过长。
计算结果如图2-图5所示,包括六足机器人迈一步过程中足端支反力、关节力和力矩。图2给出了各种不同算法求得的某一足端反力的切法比系数,其中,图2(a)是伪逆法求得的结果,图2(b)是传统优化方法求得的结果,图2(c)是遗传算法(GA)求得的结果。结果显示,伪逆法求得的支反力其切向力和法向力比率系数非常小,小于10-3,而两种优化方法求出的支反力比例系数相当,都在0.1左右,但是遗传算法求得的结果曲线不光滑,其余两条支撑腿求得的结果类似。
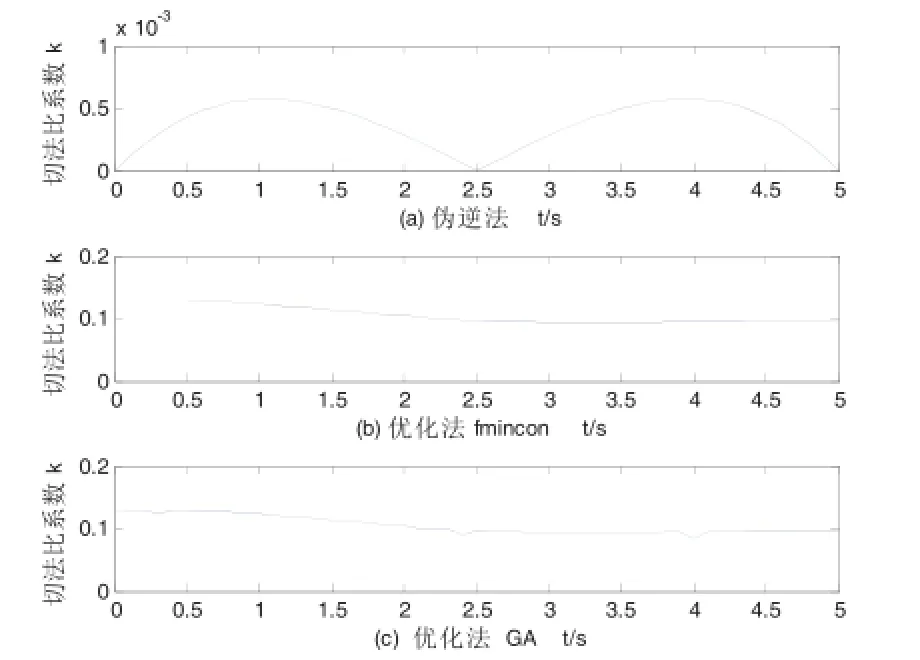
图2 一条支撑腿的切法比系数
图3 显示了三种不同方法求得的三个支撑足的足端支反力大小,结果显示,三种方法求得的结果变化趋势一致。其中,伪逆法求得的支反力比较小,另外利用优化方法fmincon和GA求得的支反力大小几乎完全一样,重合在一起,但比伪逆法求得的结果偏大。
图4显示了机器人做单步行走时,3条支撑腿的力矩变化,其中最左侧的一列是各腿关节1的力矩,最右侧的一列是各腿关节3的力矩。
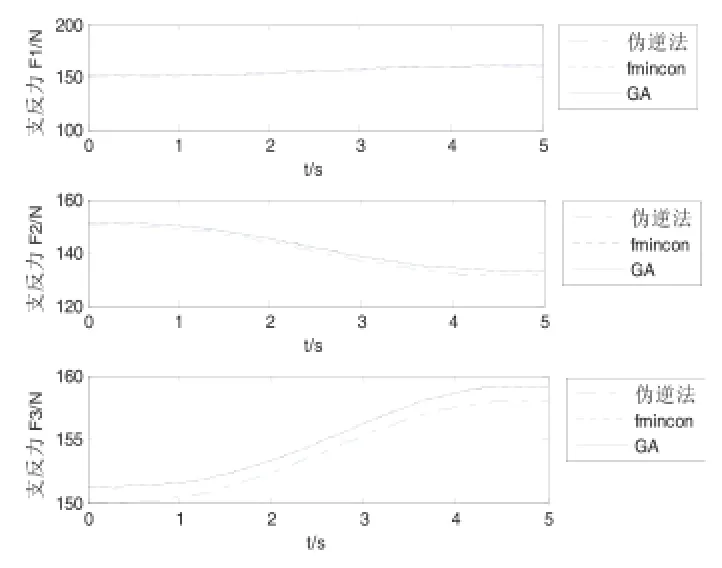
图3 三条支撑腿的支反力大小
从图4中可以看出,由于伪逆法和优化方法追求的目标不一样,所以得到的各个关节力矩有较大区别,用伪逆法求得的结果显示各条腿关节1和关节3的力矩很小,而关节2的力矩较大;两种优化算法得到的结果也是关节1和关节3的力矩小,关节2的力矩大,但差别没有这么显著。另外,利用优化算法fmincon和GA得到的各关节力矩曲线几近重合;利用遗传算法优化得到的力矩有小幅度的波动,调整遗传算法的种群大小、遗传代数等参数后,仍得不到满意的结果,且运行时间很长,效率低下。
将伪逆法求得的足端反力代入动力学方程,可以求得机器人各个关节的力矩,然后,将机器人行走每一时刻的各个关节的力矩取平方再求和;将优化方法求得的关节力矩做同样的处理,并将数据画在图5上,可以看出,伪逆法求得的关节力矩要明显大于优化法求得的关节力矩,前者大约是后者的1.3倍。虽然两种优化算法得到的力矩平方和大小曲线已经重合,但利用遗传算法求解耗时非常长。
结果表明,采用优化法求得的足端反力能使机器人在行走过程中关节力矩明显小。结合图2的结果分析可知,伪逆法得到的结果保证各个支撑足的切法比系数相等,使得机器人足端反力的切法比系数很小,这表明该算法是一种保守的足端力方案,使得机器人行走时远离打滑的状态,而优化法本质上是放松了这一约束,得到了关节力矩更优的方案。
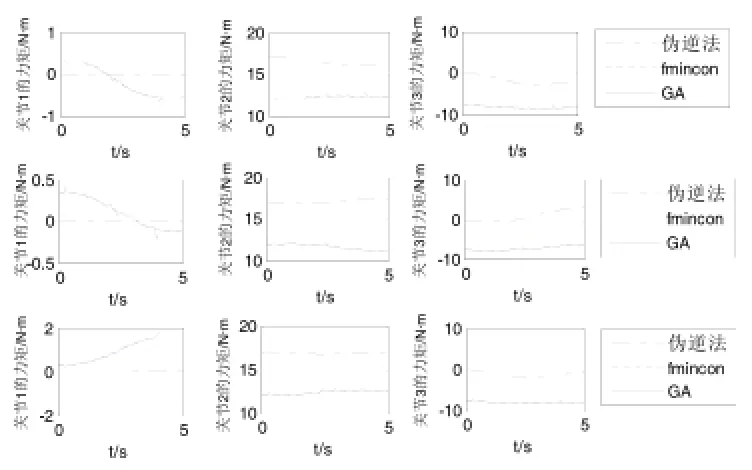
图4 三个支撑腿上的9个关节力矩的大小
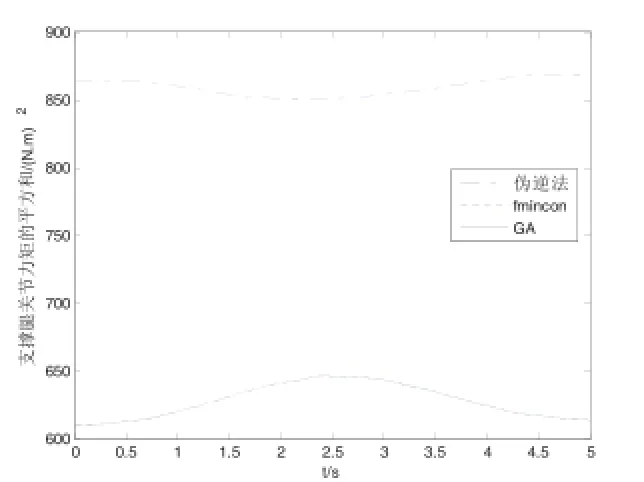
图5 三条支撑腿的关节力矩平方和
5 结论
本文介绍了关于六足机器人足端支反力分布问题的两类求解方法,即支反力求解的伪逆方法和优化方法。伪逆法本质上是以九个足端支反力分量的平方和最小为目标的算法,优化方法则以各个关节的力矩平方和最小为目标。为了比较各种方法求得结果的差异,文中用伪逆法、基于常规规划理论的优化方法和遗传算法分别实现了某六足机器人足端支反力的求解。从计算时间上看,伪逆法计算速度远远快于优化方法,有望用在控制算法中实现实时计算;从计算结果来看,伪逆法得到的结果偏于保守,能耗较大,而优化方法得出的关节力矩较小,得到了更优的足端力分配方案。针对优化方法,本文比较遗传算法和常规的优化算法求解效果,计算表明,遗传算法耗时长,而且难以收敛到光滑的关节力矩的曲线,并不适合求解这类问题。
为了实现机器人的设计分析,采用常规优化算法可以得到较满意的结果;如果从控制的观点看,采用伪逆法可以满足求解速度的要求,但得到的足端力分配方案偏于保守,基于这种方案实施控制,难以发挥机器人应有的机动性能。
[1] Kumar V R,Waldron K J.Force distribution in closed kinematic chains[J].IEEE Journal of Robotics and Automation,1988,4(6):657-664.
[2] Cheng F T,Orin David E. Efficient Algorithm for Optimal Force Distribution-The Compact-Dual LP Method[J].IEEE Transactions on Robotics and Automation,1990,6(2):178-187.
[3] 王新杰.多足步行机器人运动及力规划研究[D].武汉,华中科技大学机械电子工程,2005.
[4] Liu H Y,Wen B C. Force Distribution for the Legs of a Quadruped Walking Vehicle[J].Journal of Robotic Systems,1997,14(1):1-8.
[5] Gardner J F. Efficient computation of force distributions for walking machines on rough terrain[J].Robotica,1992,10(5):427-433.
[6] Erden M S,Leblebicioglu K. Torque Distribution in a Six-Legged Robot[J].IEEE Transactions On Robotics,2007,23(1):179-186.
[7] Roy S S,Pratihar D K. Kinematics,Dynamics and Power Consumption Analyses for Turning Motion of a Six-Legged Robot[J].Journal of Intelligent & Robotic Systems,2014,74(3-4):663-688.

