椭圆曲线加密算法的边信道攻击*

陈 力,葛万成

(同济大学中德学院,上海200092)

椭圆曲线加密算法的边信道攻击*

陈 力,葛万成

(同济大学中德学院,上海200092)

椭圆曲线加密算法是目前已知的公共密钥体系中加密强度最高的一种算法,为了将其破解,采用边信道攻击,即通过对密码机在加密过程中的功率变化的分析来尝试获取密钥信息,从而绕过了从数学上破译椭圆曲线密钥极其困难的问题。所搭建的实验平台,利用示波器探测正在运行加密程序的设备,对其中进行差分功率分析,从而找到加密规则。实验结果验证了所采用方法的有效性。

椭圆曲线加密 密钥 破解 边信道攻击

0 引 言

密码学是以研究秘密通信为目的的一门学科,对所要传送的信息采取一定的保护措施,以防止未经授权的第三方窃取信息。密码学发展至今,已经成为一门综合性的尖端技术科学。它与数学、语言学、电子学、计算机科学、信息论等学科有着日益密切的联系。与此同时,密码破译技术也随着科技的不断进步发生着日新月异的变化,借助的设备越来越先进,破译手段越来越高明。密码学与密码破译技术相互钳制,相互促进,共同向前发展。

密码是通信双方按照事先约定的法则进行信息转换的一种工具。依照密码的机制,明文变为密文,此为加密变换;变密文为明文,称为解密变换[1]。近代以前,密码主要对文字或数字进行加密、解密变换。而伴随着其他学科的发展,现在对于语音、图像、数据等信息都可以实现加密、解密过程。

20世纪70年代以来,美国学者提出了公共密钥体系,有别于传统密钥体系,即运用单向函数的数学原理,以实现加密密钥、解密密钥的分离。加密密钥是公开的,解密密钥是保密的[2]。这种新的密码体制,引起了密码学界的广泛注意和探讨,公共密钥体系近几十年来从理论到实践都发展迅速,已经成为当今密码学的主要研究方向和应用领域。

本课题研究基于椭圆曲线密码学,如何通过边道(Side-Channel)信息获取密钥信息。由于椭圆曲线加密算法的安全性非常高,通过数学算法破解的难度非常大[3],同时需要花费很长的时间。因此边信道攻击是一种比较有效的破解方式。本文通过设计实验,实现了一个通过寻找密码机加密过程中的功率变化与密文之间的关系,成功获取明文的例子。

1 边信道攻击

传统的密码分析假定对手只能访问密码设备的输入和输出对,但没有关于该设备的内部状态的知识。然而,随着边信道分析的提出,带来了一个全新的密码学分析的视角。边信道分析显示了一个密码设备,在加密过程中可以泄露其内部状态的重要信息。通过监测的密码设备加密的时间信息,温度功耗,电磁辐射或其他信息,攻击者可以获取内部数据或操作的信息,并通过分析这些信息获取加密算法的密钥,以避开数学算法破解的难题[4]。

边信道密码分析主要通过观察芯片运行过程中的功耗轨迹来获取一些与密钥相关的有用信息,特别适合于攻击具有分支结构的加密算法[5]。该方法似乎没有传统密码分析学的更加一般化,但是如今在实际破译中边信道密码分析更为强大和有效。

数学方法是分析密码学设备的有效工具,通过数学方法可以评估密码的加密强度。实际实现各种加密算法必定是通过某种硬件设备。这些硬件设备在进行加密或解密的过程中,必定有功耗或是其周围的电磁场发生变化。这些变化会涉及到密钥信息。

文中使用差分功耗分析(DPA,Differential Power Analysis)。基于DPA[6]的攻击需要大量的功率波形。DPA使用数学统计方法去分析该密码设备的密钥信息。通常一个基于椭圆曲线的DPA攻击执行如下:

第1步:选择一个椭圆曲线算法,计算该算法的中间值。这中间值是一个函数f(d,k),其中d是一个已知的非恒定的数值,k是密钥的一部分。

第2步:让对N块不同的数据进行加密或解密,并测量加密设备的功率损耗。攻击者应该知道相应的数据值d,可以表示为一个向量d=(d1,d2,…,dN),di表示第i个加密或解密的数据值。和其对应的功率曲线可以表示为p′i=(pi,1,pi,2,…,pi,T),其中T为功率曲线的长度。而对于所有的N个不同的数据块的功率曲线可以写成一个矩阵P,其尺寸为N×T[7]。

第3步:对每一个可能的密钥k计算出一个假设中间值,假设一共有K个可能的选择,可作表示为一个向量k=(k1,k2,…,kK)。对于所有的N个数据块和所有可能的密钥k,可以计算出一个大小为T ×K的假设中间值f(d,k)的矩阵V,其中的任意一个元素可以表示为

第4步:将矩阵V映射到一个假设的功率损耗值矩阵H。通过仿真,利用如汉明距离模型将每个假设中间值vi,j是映射到一个假设的功耗值hi,j。

第5步:对比假设的功率损耗值和实际测量的功率损耗值,将矩阵H的每列hi和矩阵P每列的pj相比,这种比较的结果是一个矩阵R,大小为K×T。

2 边信道攻击实验平台

图1为实验平台的示意图。实验平台包括一个安捷伦DSO9254A示波器,一个SmartFusion的测试板和基于Linux系统的计算机。而除了这些硬件组件,数据收集和处理是借助MATLAB Control Toolbox,VXI-11协议,串行通信协议。

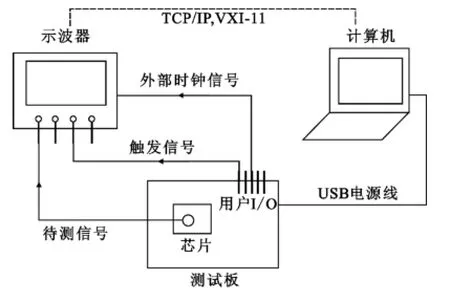
图1 实验平台示意Fig.1 Experimental platform

从图1可以看出,计算机与安捷伦示波器之间的通信是基于VXI-11协议,计算机和SmartFusion测试板通过USB连接,并且计算机通过USB连接为SmartFusion测试板提供电能。测试板通过一个用户I/O口提供外部时钟信号给示波器,同时它也提供了示波器进行测量的触发信号,使我们可以同步测量SmartFusion测试板上的加密设备的功耗。

3 攻击过程及数据分析

按照预测中间值(0或1),我们将功率损耗曲线分成对应的两部分。将预测中间值是0的功率损耗曲线相加并求平均值,得到预测值为0的平均功率损耗曲线;将预测中间值是1的功率损耗曲线相加并求平均值,得到预测值为1的平均功率损耗曲线。我们计算出两条功率损耗曲线的差别。如果有明显差异曲线的峰值,则假设是正确的。否则,假设是错误的。

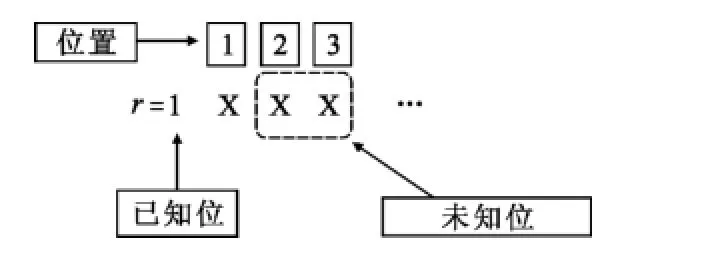
图2 基于比特模式的DPA攻击原理示例Fig.2 Principle of DPA attacks based on bits

图2显示了基于比特模式的DPA攻击。标量r的第一位是已知的,其值是1。攻击的目的是试图找出其余位的值。根据蒙哥马利阶梯算法,1号位的值可由确2号位和3号位的值决定。具体攻击过程可以表示如图3所示。

图3 基于比特模式的DPA攻击过程示意Fig.3 Process of DPA attacks based on bits

实验结果显示,4P、5P和8P假设的差异曲线有明显的峰值出现,而6P和7P假设的差异曲线没有明显的峰值出现(见图4～图8)。在加密过程中,如果预测的中间值被使用了,如图4显示,那么在差异曲线中将会出现峰值。这意味着,7P假设没有在加密过程中出现。根据图3可以断定,在标量r的第1位是0。由于4P假设的峰值高于基于6P假设的峰值,那么它可以猜测标量r的第二位为0的概率更大。

4P和5P的差异曲线有两个峰(见图4和图5),它们代表从寄存器到寄存器的一个读操作和一个写操作。但在图8中只有一个峰值,这是因为,我们只观察两个位,与8P假设的差异曲线峰值已经超出示波器的观测范围。

图4 4P的差异曲线Fig.4 Cross-correlation function for 4P

图5 5P的差异曲线Fig.5 Cross-correlation function for 5P

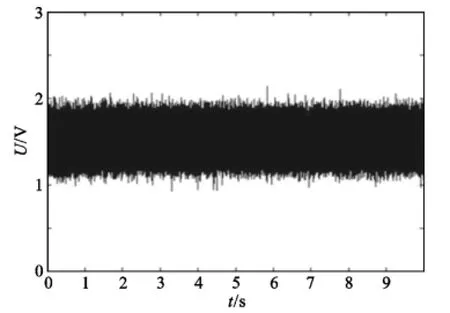
图6 6P的差异曲线Fig.6 Cross-correlation function for 6P

图7 7P的差异曲线Fig.7 Cross-correlation function for 7P

图8 8P的差异曲线Fig.8 Cross-correlation function for 8P

4 结 语

虽然进行边信道攻击的前提条件(即获得密码机)比较苛刻,但它在应对复杂的椭圆曲线编码时可以得到令人满意的结果。因此边信道攻击仍是一种有效的密码破解技术。更重要的是,通过对边信道攻击的模拟,我们对其攻击手段和特点进行研究,使现有的加密算法能够得到针对性优化,从而能够防范此类攻击,提高加密的安全性。所谓知己知彼百战不殆,边信道攻击的分析研究对于密码学的发展具有重大意义。

[1] JOACHIMS Woboda,SPITZS Tephanand,PRAMATERFTAKIS Michael.Kryptographie und IT-Sicherheit: Grundlagen und Anwendungen[J].ViewegTeubner, 2008,21(04):199-202.

[2] KOBLITZ Neal.Elliptic Curve Cryptosystems[J].Mathematics of Computation,1987,48(02):203-209.

[3] MILLER V.Use of Elliptic Curves in Cryptography[C]// Proc 4th IEEE Conf Evolutionary Computation.Berlin: Springer-Verlag,1996:417-428.

[4] STALLINGS William.Cryptography and Network Security Principles and Practices[M].New York:House of Electronics Industry,2006:210-224.

[5] 叶宾.安全芯片之安全性分析[J].通信技术,2013, 46(08):91-92.

YE Bin.Security Analysis of Security Chip[J].Communications Technology,2013,46(08):91-92.

[6] KOBLITZ Neal.The State of Elliptic Curve Encryption Algorithm[J].Designs Codes and Cryptography,2000, 19(01):173-193.

[7] KOCHER P.Timing Attacks on Implementations of Diffie -Hellman,RSA,DSS,and Other Systems[C]//PACIIA1996.USA:Springer-Verlag,1996:109-113.

CHENLi(1990-),male,graduate student,mainly engaged in the research of signal and information processing.

葛万成(1964—),男,博士,教授,主要研究方向为信号与信息处理。

GE Wan-cheng(1964-),male,Ph.D.,professor,principally working at signal and information processing.

Side-Channel Attack on Elliptic Curve Encryption Algorithm

CHEN Li,GE Wang-cheng
(Chinese-German School for Postgraduate Studies,Tongji University,Shanghai 200092,China)

Elliptic-curve encryption algorithm is currently known as the best algorithm in the public-key cryptosystem.In order to break it,a side-channel information attack is designed and used.With near-field probe to measure the power traces generated by the chip,the relation between the power traces and secret key is tried to find out.In this way,the mathematical problems can be avoided.In the experiment,oscilloscope is used to acquire the data from the crypto device and then to analyze them.From the differential power analysis,the secret key may be found.The experiment shows that the side-channel attack could work effectively.

elliptic curve encryption;secret key;decipher;side-channel attack

TN918

A

1002-0802(2014)09-1062-04

10.3969/j.issn.1002-0802.2014.09.017

陈 力(1990—),男,硕士研究生,主要研究方向为信号与信息处理;

2014-06-23;

2014-07-24 Received date：2014-06-23;Revised date：2014-07-24