EXCEL函数在混合成本分解中的巧用
王雍欣
EXCEL函数在混合成本分解中的巧用
王雍欣
混合成本分解是成本性态分析的前提和基础。传统的混合成本分解方法工作量大,计算复杂,难以记忆。利用EXCEL的CORREL、SLOPE和INTERCEPT函数可以有效简化混合成本分解问题。
混合成本分解;CORREL;SLOPE;INTERCEPT
一、引言
成本性态又称成本习性,是指成本总额的变动与业务总量(产量或销售量)之间的依存关系。成本总额与业务总量的依存关系是客观存在的,而且具有规律性。管理会计作为决策会计的角色,其许多决策方法特别是短期决策方法都必须借助于成本性态这一概念。按成本性态可以将企业的全部成本分为固定成本、变动成本和混合成本三类。固定成本是指其总额在一定期间和一定业务量范围内,不受业务量变动的影响而保持固定不变的成本。变动成本是指在一定的期间和一定业务量范围内下随业务量的变动而成正比例变动的成本。在实际工作中,许多成本往往介于固定成本和变动成本之间,它们既非完全固定不变,也不随业务量成正比例变动,因而称为混合成本。混合成本的基本特征是发生额的高低虽然直接受业务量大小的影响,但不存在严格的比例关系。决策时需要将混合成本按性态分解为变动成本和固定成本,只有这样才能为决策所用。混合成本的分解方法,一般有历史成本分析方法、工程分析法、账户分析法和合同确认法等。这些方法工作量大,计算复杂,难以记忆。笔者探讨利用EXCEL函数法来简化混合成本分解问题。
二、EXCEL函数与基本方法
简化混合成本分解问题使用的EXCEL函数有CORREL、SLOPE和INTERCEPT。
1.CORREL函数
(1)含义:返回单元格区域array1和array2之间的相关系数。
(2)语法:CORREL(array1,array2)。
(3)参数:array1是第一组数值单元格区域;array2是第二组数值单元格区域。
2.SLOPE函数
(1)含义:返回经过给定数据点的线性回归拟合线方程的斜率(它是直线上任意两点的垂直距离与水平距离的比值,也就是回归直线的变化率)。
(2)语法:SLOPE(known_y’s,known_x’s)。
(3)参数:Known_y’s为数字型因变量数组或单元格区域,Known_x’s为自变量数据点集合。
3.INTERCEPT函数
(1)含义:利用现有的x值与y值计算直线与y轴的截距。截距为穿过已知的known_x's和known_y's数据点的线性回归线与y轴的交点。
(2)语法:INTERCEPT(known_y's,known_x's)。
(3)参数:Known_y's为因变的观察值或数据集合;Known _x's为自变的观察值或数据集合。
4.基本方法
运行EXCEL程序,分两列从上至下分别录入自变量(X)列数值和相应的因变量(Y)列数值,选择空白单元格,点击“插入”选择“函数”,出现插入函数对话框,在“选择类别”中选择“统计”,在下面的滚动菜单中选择“INTERCEPT”函数(求线性回归方程的截距a),单击“确定”后出现“函数参数”对话框,在Known_y’s框中选择Y值区域,在Known_x’s框中选择X值区域,对话框下方自动显示计算结果,可求出a。同样的方法,在滚动菜单中选择“SLOPE”函数(求线性回归方程的斜率b),可求出b。由此,可得出混合成本分解模型y=a+bx。
三、应用举例
例:已知某公司的2013年1-6月份的有关资料如表1所示。
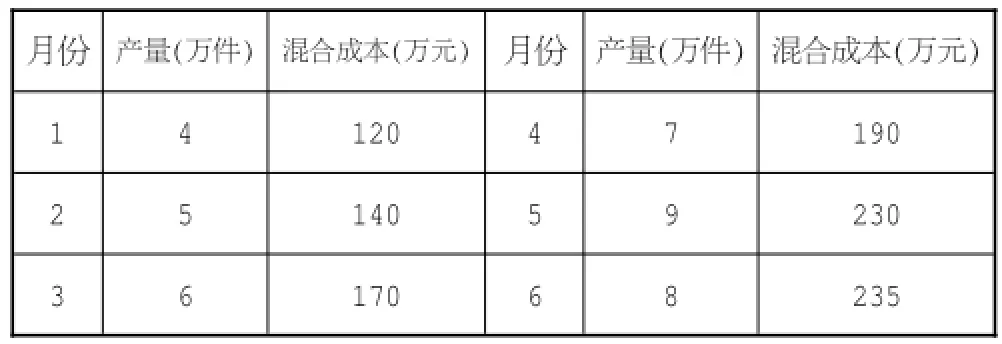
表1
1.传统混合成本分解方法一:高低点法
高低点法是以最高业务量的混合成本与最低业务量的混合成本之差,除以最高业务量与最低业务量之差,计算出单位变动成本,然后再代入总成本公式y=a+bx,根据最高业务量或最低业务量的数据,即可分解出混合成本中的固定成本。计算过程如下:
解:本例中最高点业务量为9万件,对应的混合成本为230;最低点业务量为4万件,对应的混合成本为120,根据定义:
单位变动成本b=(230-120)/(9-4)=22(万元)
固定成本a=230-22*9=32(万元)
因此混合成本分解模型为:y=32+22x
2.传统混合成本分解方法二:回归直线法
回归直线法是运用数理统计中常用的最小平方法的原理,对所观察到的全部数据加以计算,从而勾画出最能代表平均水平的直线。这条通过回归分析而得到的直线就叫回归直线,它的截距就是固定成本a,斜率就是单位变动成本b。如果采用回归分析法进行成本性态分析,计算过程如下:
解:根据历史资料数据列表,计算出n,∑x,∑y,∑xy,∑x2,∑y2的值。计算结果如表2所示。
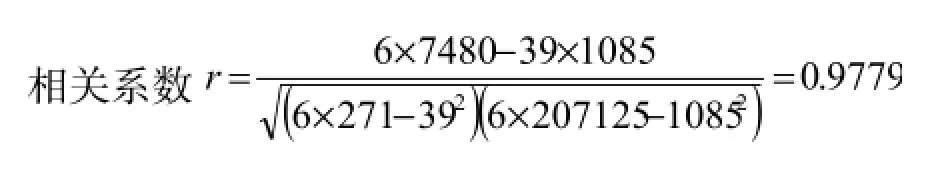
因为r趋向于+1,表明x和y基本正相关,可以建立成本模型。
则:a=(271×1085-39×7480)÷(6×271-392)≈22.05(元)
b=(6×7480-39×1085)÷(6×271-392)≈24.43(元/件)
故该企业的成本模型为:y=a+bx=22.05+24.43x
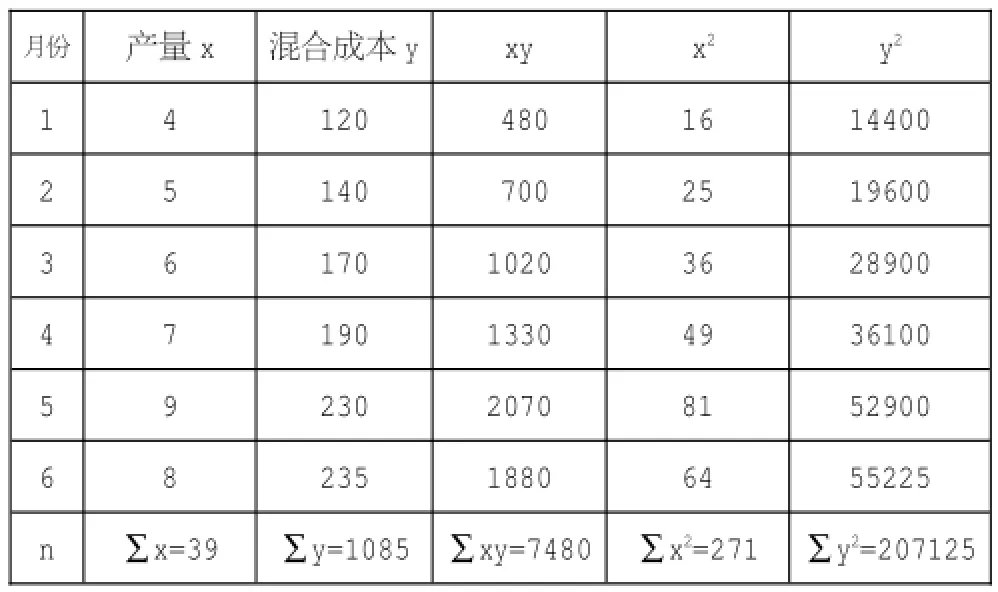
表2 回归分析计算表
3.EXCEL函数法
如果采用EXCEL函数处理,计算步骤和过程如下:(1)在EXCEL空白表中录入数据,见表3。
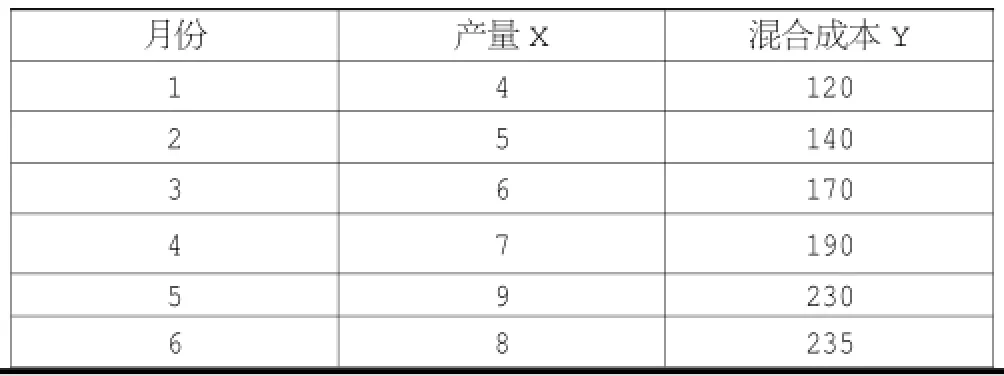
表3
(2)在空白单元格内插入统计函数CORREL。
选择空白单元格——插入——函数——统计——选择CORREL,结果如图1:
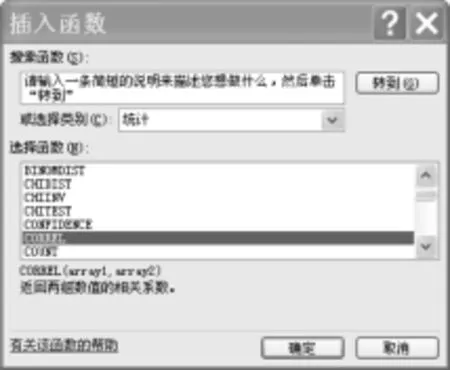
图1:插入CORREL函数
(3)图1确定后,选择区域X数据区域和Y数据区域,结果如图2。从图2中可见相关系数r为0.977888199。
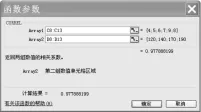
图2:CORREL函数参数
(4)在空白单元格内插入统计函数SLOPE。
选择空白单行格——插入——函数——统计——选择SLOPE,结果如图3。
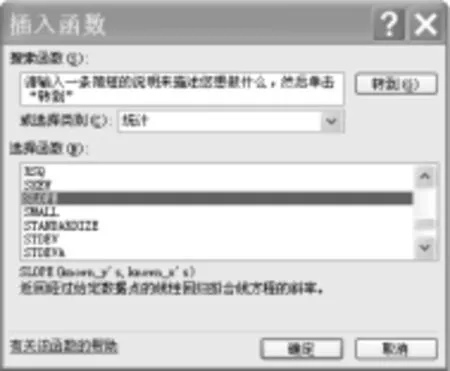
图3:插入SLOPE函数
(5)图3确定后,选择区域Y数据区域和X数据区域,结果如图4。从图4中可见单位变动成本b为24.42857143。
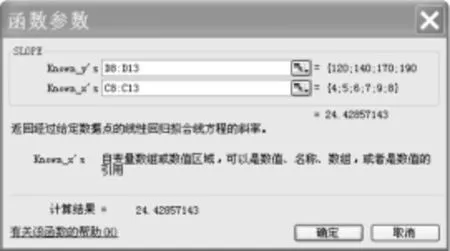
图4:SLOPE函数参数
(6)在空白单元格内插入统计函数INTERCEPT。选择空白单行格——插入——函数——统计——选择INTERCEPT函数,结果如图5。
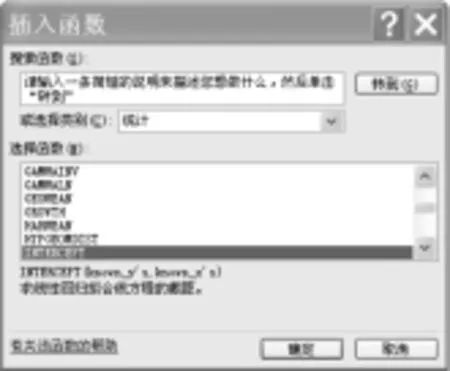
图5:插入INTERCEPT函数
(7)图5确定后,选择区域Y数据区域和X数据区域,结果如图6。从图6中可见固定成本a为22.04761905。如果保留两位小数,由此可得混合成本分解模型为y=24.43+22.05b。
四、结论
对比上述三种方法可以发现:高低点法的优点在于简便易行,易于理解。缺点是由于它只选择了历史资料中的两组作为计算依据,使得建立起来的成本性态模型很可能不具有代表性,容易导致较大的计算误差。如固定成本为32万元,与后两种方法计算的24万元相差8万元。与高低点法相比,回归直线法由于选择了包括高低两点在内的全部观测数据,因而避免了高低点法中高低两点的选取带来的偶然性,比较科学,精确度高,但比较麻烦,计算复杂,公式不易记忆。EXCEL函数法,不但科学,精确度更高,操作简单方便。
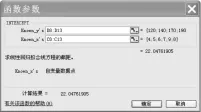
图6:INTERCEPT函数参数
[1]宗国恩.管理会计学.西南财经大学出版社,2012年1月.
[2]Excel Home.Excel2010实战技巧精粹,人民邮电出版社,2013年4月.
(作者单位:安阳工学院经济管理学院)

