高分子发泡材料中孔径分布的计算机模拟

滕 鑫， 鞠明杰， 唐颂超， 徐世爱， 李水强

(华东理工大学 a. 材料科学与工程学院; b. 体育科学与工程学院， 上海 200237)

0 引 言

泡沫塑料是一种新型材料，具有质轻、强度高、热导率低、隔热性能好、能吸收冲击载荷、优良的缓冲性能等共同特性[1-2]。泡沫塑料工业在近十几年发展极快，特别是在工业发达国家，不仅在品种、产量和质量等方面提高显著，而且理论研究也在逐步深入。在众多泡沫塑料性能的影响因素中，内部泡沫的孔径大小及分布对泡沫塑料的多项性能有十分重要的影响，如：力学性能，热膨胀性能，隔热性能，气体渗透性能，尺寸稳定性及吸水率等。因此，寻找一种方便有效的试验方法对泡沫孔径的大小及分布进行精确的测量对推动泡沫塑料工业的发展具有重大的意义。传统的泡沫孔径大小及分布的测试方法有很多，如双气路色谱法[3]、中流量孔径法[4]、汞压入法[5]、气泡法[6-7]及其他试验方法[8]，最直观的方法基本都是通过照片来观测孔径分布。但通过照片观测只能了解某一剖面的孔径分布情况，无法反映出整个泡沫塑料体中孔径分布的真实情况[9]。为了提高照片观测的可靠程度，本文提出用计算机来模拟孔径分布，找出孔径分布的规律，通过泡沫塑料体剖面的孔径分布情况分析出泡沫塑料体内部真实的孔径分布情况，使通过照片观察孔径分布这个方法能发挥更大的作用。

1 实验方案

然后分析孔径分布，单孔径分布是最基本的分布，也是本次实验的基础。影响单孔径分布的参数主要有原始孔径和重复次数，分别改变其大小，分析概率图形随之产生的变化，找到单孔径分布统计的一般规律。

找到单孔径分布的规律后，按照由易到难的顺序，进行双孔径分布的研究。双孔径分布是单孔径分布的延伸，同时也是从单孔径分布到多孔径分布的过渡[15]。影响双孔径分布的参数与单孔径分布相同，也是原始孔径和重复次数。但双孔径分布中包括两种原始孔径和重复次数，4个参数对于图形都有影响，需要逐一分析研究，找到双孔径分布的规律，所以它的情况比单孔径分布要复杂。通过双孔径分布的分析可以进一步加强对孔径分布基本情况的了解，在编程技术上也可以为随后复杂的多孔径分布有一定帮助。

由于正态分布能基本准确地模拟出孔径分布的真实情况，它也就成为了本次实验的最终环节，也是实验的难点。

影响正态孔径分布的参数有σ和μ，当σ和μ确定后，正态曲线就完全确定了。σ和μ不同，正态曲线的位置和形状则不同。σ是位置参数，它的大小决定曲线在x轴上的位置，μ是形状参数，它的大小决定曲线的高矮胖瘦。

在实验中，对于正态分布的研究可以分为三部分，首先是正态分布的一般分析，通过给定σ和μ来画出正态分布图形，改变σ和μ来找到正态孔径分布的一般规律；其次是σ的比较，在μ给定的情况下改变σ的值来改变图形，通过前后图形的比较来找出σ对于正态分布图形的影响；最后是μ的比较，在σ给定的情况下改变μ的值来改变图形，通过前后图形的比较来找出μ对于正态分布图形的影响。

2 实验过程及实验程序

实验选用的开发平台是Microsoft Windows操作系统下的Visual Basic(VB)。该程序主要由3部分构成，分别对单孔径分布、双孔径分布和正态孔径分布这3种比较典型的孔径分布改变其重要参数，研究孔径分布曲线随参数改变所产生的变化，希望能找出孔径分布规律。对于单孔径分布和双孔径分布，均是在主界面上输入原始孔径和重复次数，通过计算得到孔径分布概率图和分布曲线图，以图形的方式显示给用户。由用户通过输入不同的原始孔径和重复次数，比较图形产生的变化，从而找到较简单的孔径分布规律。对于较复杂的正态孔径分布，先输入σ和μ，计算得到孔径分布概率图和分布曲线图，随后分别改变σ和μ，比较图形产生的改变，找出σ和μ对图形的影响，从而得到正态孔径分布的规律。程序总体模块结构见图1。

图1 程序总体模块结构图

实验中选取单孔径分布、双孔径分布、三角孔径分布和正态孔径分布进行分析。

2.1 单孔径分布

单孔径分布是指泡体中孔径均一的泡沫塑料，但气泡在泡体中的分布形式是随机的，这就造成了在泡体中随机剖一刀所形成的剖面上的气泡孔径也是随机的。实验中，把泡体中均一的孔径称为原始孔径，把剖面上随机分布的孔径称为剖面孔径，实验目的就是寻找剖面孔径与原始孔径之间的关系，见图2。

图2 单孔径分布统计示意图

假设单孔径分布的原始孔径半径为z，重复次数为n。在单孔径分布的统计实验中，先在单孔径分布的泡沫塑料泡体中选取一个高度为4z的泡体作为实验研究的对象。在研究对象中分别以随机数的形式得到在2z～-2z之间的随机圆心坐标数组x(i)= 4cz-2z(c为0～1的随机数)和在z～-z之间的随机切线坐标数组q(i)=2dz-z(d为0～1的随机数)。在分别得到圆心坐标数组和切线坐标数组后，将圆心坐标数组减去切线坐标数组，得到圆心到切线的距离。如果这段距离大于原始孔径z，表示切线 没能切到圆，不产生切面孔径；如果距离小于或等于原始孔径z，表示切线切到了圆，产生切面孔径：

在得到切面孔径数组r(i)之后，对它进行整理和排序，随后以r(i)作为横坐标，纵坐标恒定，得到切面孔径分布图；以r(i)为横坐标，20i作为纵坐标，得到切面孔径概率分布图；以r(i)为横坐标，5/[r(i+1)-r(i)]作为纵坐标，得到切面孔径概率密度图。

得到剖面孔径分布的照片就可以将照片上的孔径换算成概率密度图和概率分布图，如果符合单孔径分布图形的特征就可以认为这种剖面的泡体是单孔径分布的泡沫塑料。单孔径分布的系统流程如图3所示。

图3 单孔径分布系统流程图

从图4可以看出,在单孔径分布中孔径并不是均匀分布的，越接近原始孔径处，抽样越密；在原始孔径处，抽样最密，概率密度也达到最大值。从概率分布图中可以看出,起初分布曲线比较平缓，越接近原始孔径处曲线越陡峭。有了这3幅图后，我们可以通过泡沫塑料剖面孔径的分布情况判断出这个泡体内部是否是

图4 原始孔径为0.5，重复次数100的单孔径分布图

单孔径分布，原始孔径是多少。

2.2 双孔径分布

双孔径分布的实验原理和产生的图案与单孔径分布相似，不过在双孔径分布的泡沫塑料中有2个原始孔径。这样，在双孔径分布泡沫塑料剖面上的孔径分布情况就要比单孔径分布的情况复杂。双孔径分布的系统流程图如图5所示。

图5 双孔径分布系统流程图

由图6可以看出,双孔径与单孔径分布类似，越接近原始孔径处抽样越密，概率密度越高。一般较小原始孔径处的概率密度较高，这应该是因为较小的原始孔径不仅含有自己的抽样，还包括较大的原始孔径抽样。概率分布曲线也与单孔径分布相同，起初较平坦，越接近原始孔径越陡峭。小孔径处曲线更陡峭也是因为包括两种抽样的关系。

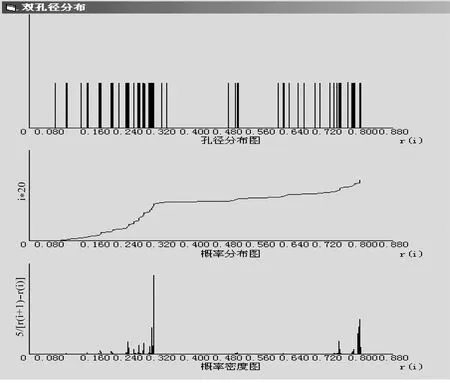
图6 原始孔径分别为0.3和0.8，重复次数为

2.3 正态孔径分布

正态分布孔径统计程序的编制可以分为：① 根据μ和σ画出正态分布曲线；②σ的比较。在μ恒定的情况下，通过输入不同大小的σ值来分析得出σ对于正态分布曲线的影响；③μ的比较。在σ恒定的情况下，通过输入不同大小的μ来分析得出μ对于正态分布曲线的影响。

(1) 在第一部分的研究中，先随机产生0～2的随机数的数组r1(i)作为x，再根据正态分布概率密度计算式

(2) 第二和第三部分的研究与第一部分相似，不过要输入不同的μ和σ进行计算，得到概率密度图和概率分布图，分析得出μ和σ对于正态分布图形的影响。正态孔径分布的系统流程如图7所示。

由图 8可以看出,随着σ逐渐增大，正态分布的峰值逐渐减小，而峰的宽度逐渐增大，但总面积保持不变。另外，正态分布孔径的峰值比原始孔径要略大，这是正态分布与单、双孔径分布的不同。由图9 可以看出,随着μ逐渐增大，正态分布的峰的形状保持不变，而峰的位置渐渐的向右偏移。另外，随着μ的增大，正态分布孔径的峰值与原始孔径的峰值之间的距离也逐渐增大，这是μ对于正态分布图形的影响。

3 结 语

在单孔径分布中主要讨论原始孔径和重复次数的变化对于概率图形的影响以及单孔径分布的一般规律。通过对图形变化的分析发现原始孔径影响峰值出现的位置，而重复次数影响密度曲线的平坦程度。对单孔径分布的分析研究主要用于判断某种泡沫塑料内部是否是单孔径，原始孔径是多少。

图7 正态孔径分布及其比较系统流程图

图8 σ的比较图9 μ的比较

双孔径分布所要讨论的参数与单孔径分布相同，也是原始孔径和重复次数，只不过比单孔径分布要复杂，需要考虑两组原始孔径和重复参数。在双孔径分布图上可以明显的看出较小孔径处的概率密度较大，概率曲线也比较陡峭，这应该是由于较小孔径处不仅包括它本身的孔径分布，还包括了一部分较大孔径的孔径分布。

在正态分布图中可以看出，正态分布概率密度的峰值与孔径分布的峰值之间有一定的差值，这差值随着μ的增大而增大。

在正态分布中遇到的问题是从理论上来说，随着σ的减小，概率密度峰值和孔径分布峰值之间的差值应该减小，但从模拟情况来看σ的变化对于差值没有影响，这是理论与实际之间的差异。

[1] 滕 鑫，唐颂超，李水强. 计算机模拟在材料实验教学中的应用[J].实验技术与管理，2013，30(5)：67-69,82.

TENG Xin,TANG Song-chao,LI Shui-qiang.Research and exploration of computer simulation utilization in materials experimental teaching[J].Experimental Technology and Management，2013，30(5)：67-69,82.

[2] 苏国钧，肖鹏飞，禹 毅.孔径分布色谱法测定数据的计算机处理[J].工业催化，1998(3)：59-62.

SU Guo-jun,XIAO Peng-fei,YU Yi.Aperture Distribution Chromatographing and Its Data-processing by Computer[J]. Industrial Catalysis，1998(3):59-62.

[3] Naoki Nishiyama, Tadashi Yokoyama, Shingo Takeuchi. Size distributions of pore water and entrapped air during drying-infiltration processes of sandstone characterized by water-expulsion porosimetry [J]. Water Resources Research，2012,48 (9)：50-56.

[4] 关 岳，孙钦莲，吴先燕. 比表面积和孔径分布测定与计算方法的改进[J].化学学报,1990,48(4)：424-430.

GUAN Yue,SUN Qin-lian,WU Xianyan.Improvements of Determination and Calculation of Specific Surface Area and Pore Distribution[J].Acta Chimica Sinica, 1990,48(4)：424-430.

[5] 丁祥金,张梓州，鲍志勤.泡点法测定微孔孔径分布的改进算法[J].无机材料学报，2000,15(3)：493-498.

DING Xiang-jin,ZHANG Ji-zhou,BAO Zhi-qin.Improved Calculating Way for the Micro-pore-size Distribution Measured by Bubble-point Methods[J]. Journal of Inorganic Materials,2000,15(3)：493-498.

[6] 方再根.计算机模拟和蒙特卡洛方法[M].北京：北京工业学院出版社，1988.

[7] Li Hu,Yang jian-yu,Su peng-cheng,etal. Computer aided modeling and pore distribution of bionic porous bone structure[J]. J Cent South Univ,2012, 19 (12)：3492-3499.

[8] 周富臣.正态分布及其应用[J].上海计量测试,2001(3)：15-19.

ZHOU Fu-chen. The normal distribution and its application[J]. Shanghai Meassurement and Testing, 2001(3)：15-19.

[9] 黄 英,金彦任,黄振兴. 活性炭孔径分布测定与计算中的一些问题研究—对几种孔径分布计算模型的分析比较[J]. 离子交换与吸附,2012,28 (2):176-182.

HUANG Ying,JIN Yan-ren,HUANG Zhen-xing.Study about the relationship between activated carbon pore size distribution measurement and calculation[J]. Ion Exchange and Adsorftion,2012,28 (2):176-182.

[10] GONG Guo-zhuo, XIE Qiang, ZHENG Yan-feng,etal.Yun-fa.Regulation of pore size distribution in coal-based activated carbon[J].New Carbon Mmterials,2009,24(2):141-145.

[11] Juqing Cui, Shuguang Han, Zhaobing Zhou,etal. Size-dependent aggregation behavior in monodisperse silica: a nitrogen adsorption study[J]. Surface and Interface Analysis, 2012, 44 (2): 66-169.

[12] Ghazanfari M H, Rashtchian D, Kharrat R,etal. Capillary Pressure Estimation Using Statistical Pore Size Functions[J]. Chemical Engineering & Technology,2007, 30 (7): 862-869.

[13] Bird N R A, Preston A R, Randall E W,etal. Measurement of the size distribution of water-filled pores at different matric potentials by stray field nuclear magnetic resonance[J]. European Journal of Soil Science, 2005, 56 (1): 135-143.

[14] Anna J Gijsbertsen-Abrahamse, Remko M Boom. Why liquid displacement methods are sometimes wrong in estimating the pore-size distribution[J]. AIChE Journal, 2004, 50 (7): 1364-1371.

[15] Chiang C L, Wu T C, Wang Y J. Enzyme loading in a solid support with nonuniform pore size distribution[J]. Biotechnology and Bioengineering,1990, 35 (10): 976-982.

* 要切实改变重理论轻实践、重知识传授轻能力培养的观念，注重学思结合，注重知行统一，注重因材施教，以强化实践教学有关要求为重点，以创新实践育人方法途径为基础，以加强实践育人基地建设为依托，以加大实践育人经费投入为保障，积极调动整合社会各方面资源，形成实践育人合力，着力构建长效机制，努力推动高校实践育人工作取得新成效、开创新局面。

摘自《教思政[2012]1号文件》