基于S型函数的α稳态分布脉冲噪声有源控制
李 沛, 宋晓娜, 侯晓霞, 张景荣
(北京信息科技大学 机电实习中心, 北京 100192)
0 引 言
有源噪声控制(Active Noise Control,ANC)是一种主动噪声控制技术,其基本理念是基于声波的相抗相消原理,系统通过控制输出主动产生一个声场来抵消现有声场,进而达到抑制或消除噪声的目的。噪声控制基本原理波形如图1所示。用输入传声器采集输入噪声信息,即时处理后得到一个反相信息,再用扬声器(次级声源)“实时”播放反相信息。反相信号(消噪波)与噪声波叠加相抗相消,从而使剩余噪声波形幅值大大减小,噪声得以控制[1-2]。
图2为管道ANC基本框图。从输入点输入参考信号x(n)(取自输入传声器)和误差信号e(n)(取自误差传声器),2个信号通过ANC控制器,经过算法处理,输出控制 信号y(n)驱动消声扬声器工作,产生和主噪声幅值相等、相位相反的次级声信号,两者相互抵消,有效衰减和抑制了噪声。
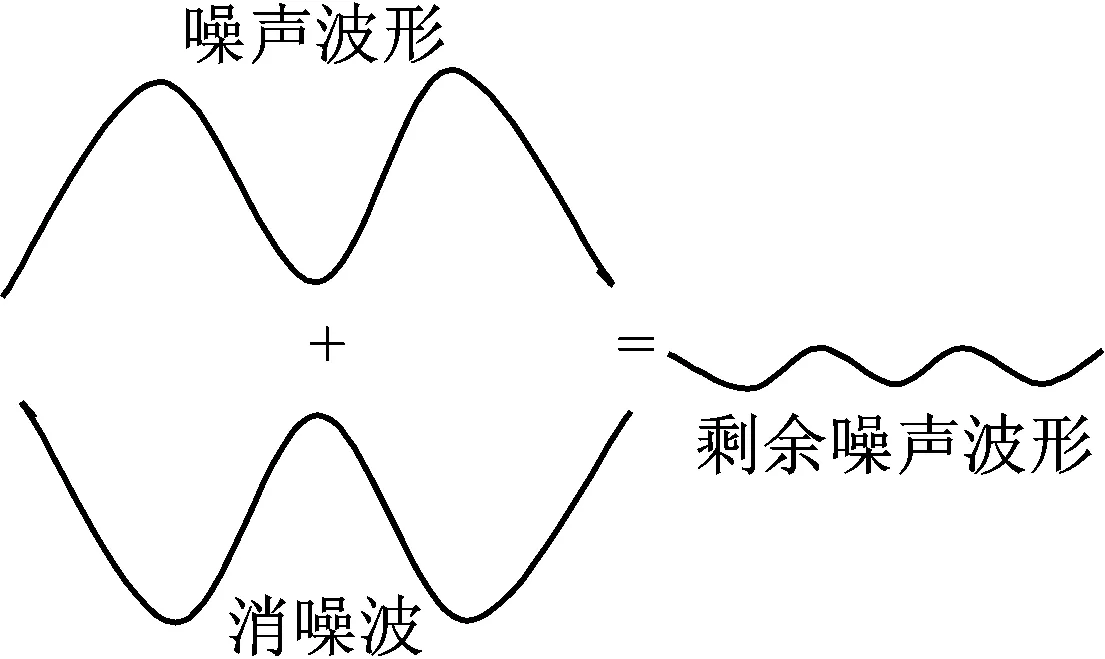
图1 噪声控制基本原理

图2 管道ANC基本框图
1 经典FXLMS算法[3-5]
FXLMS算法是ANC中最具代表性的算法,基于FXLMS算法的ANC如图3所示。FXLMS算法是自适应前馈算法,因其能有效地消除噪声,算法简单易行、容易实现、稳定有效,鲁棒性强等特点被广泛应用。FXLMS算法的联机噪声控制程序如下:

图3 基于FXLMS算法有源噪声控制
(1) 从输入点输入参考信号x(n)、和误差信号e(n)。
(2) 计算抗噪声信号y(n),
其中:Wi(n)是自适应滤波器W(z)在n时刻的系数;N是滤波器W(z)的顺序。
(3) 输出抗噪信号y(n)到输出点用以驱动消声扬声器工作。
(4) 计算滤波x转换量x′,
(5) 使用FXLMS算法计算自适应滤波器的更新系数方程,
wi(n+1)=wi(n)-μe(n)x′(n-i)
i=0,1,…,N-1
其中,μ为步长。
(6) 为下一次迭代重复该过程,记录该算法需要的存储单元总数是2(N+M)乘以参数。
2 脉冲噪声有源控制
2.1 脉冲噪声对人体健康的影响
自然界中的噪声主要有两大类:① 噪声强度波动范围在5 dB以内的连续性噪声,是稳态噪声,如电机产生的连续稳定的噪声;② 非稳态噪声, 如瞬时、周期起伏、脉冲、无规则噪声。
医学研究表明:非稳态噪声听力损伤的检出率明显高于稳态组,脉冲噪声危害程度更为明显,如锻锤、冲压、射击等产生的脉冲噪声。此种噪声具有突变、高能和覆盖频率范围广等特点。对作业工人听觉系统的影响在低工龄段已经表现出来,脉冲噪声被公认为对听力损伤出现早、危害重。冲压工人在强烈脉冲噪声环境中工作,常有心悸、头昏、恶心的感觉,心电图监测可看出ST段异常、T波改变、R-Q间期增长等症状。一次或多次接触高强度脉冲噪声可导致不可逆的严重听力损伤[6-7]。由此可见,对脉冲噪声进行控制具有很大的意义。目前,在ANC方面已取得了很大进步,但大部分是关于高斯分布稳态噪声控制,有关非高斯分布脉冲噪声控制的研究还处于探索阶段。
2.2 α稳定分布脉冲噪声
研究脉冲噪声,通常采用对称α( 0<α<2) 稳定分布 ( SαS)来建模。如果随机变量x存在参数,使其特征函数为:

式中:
则随机变量x服从稳定分布。α稳定分布的特征指数(0 <α< 2)属于非高斯分布,有无界二阶矩。脉冲噪声的几大特点决定了对它的有源控制还处于摸索研究阶段,脉冲噪声不符合高斯分布特性;具有尖峰和厚尾统计特征的概率密度函数;只有阶数小于α阶的分数低阶矩是有界的;不存在有界二阶矩;脉冲噪声还具有重复性。图4为不同α值的概率密度分布曲线。从图中可以看出,α值从2~0.5逐渐变小,分布拖尾逐渐变厚,脉冲特性越发显著;相反,随着α值变大,所对应分布的拖尾变薄,脉冲特性减弱。

图4 不同α条件下的概率密度函数
脉冲噪声往往具有无穷二阶矩,因此基于FXLMS算法的均方-误差准则,对于脉冲噪声而言,不再是一种适合的优化准则。
2.3 脉冲噪声ANC算法
针对脉冲噪声的特点,国内外关于ANC算法主要有以下几种。
(1) FXLMP算法、FXLMAD算法。此类算法主要针对脉冲噪声不存在有界二阶矩,所以采用p阶矩(分数低阶矩)代替二阶矩。FXLMP算法需要获得α先验信息、计算量大,如先验信息不足,系统可能发散导致不稳定。FXLMAD算法是FXLMP算法特例(p=1),系统稳定性能好,但收敛速度缓慢。
(2) 加窗算法、改进归一化FXLMS算法。此类算法主要针对脉冲噪声的概率密度函数具有尖峰和厚尾的统计特征,用于限制参考样本幅值。加窗算法的算法简单、稳定性和收敛性好,但需离线估计阀值,阀值的合适估算非常关键,以防止算法停止更新。改进归一化FXLMS算法算法简单,不需设定阀值和α先验信息,非常实用。但该算法没有经过严密证明,只能算是一种直觉的改进。
(3) 迭代学习控制算法。主要针对脉冲噪声具有重复性的特点。此种算法值得期待,但由于实际环境的时变性,系统的鲁棒性需要关注讨论。
(4) 非线性变换算法[8-9]。FxatanLMS 算法、FxlogLMS算法。基于α稳定分布信号建模的脉冲噪声没有有界的二阶矩,即方差不存在,那么以最小均方误差(二阶矩)为准则的经典ANC算法(最小均方算法FXLMS)将不再是适合的优化准则。我们就考虑使用非线性预处理方法,使变换后的过程具有二阶统计量,然后利用通常的LMS等方法进行处理,减少基于最小p范数的方法所带来的计算量,又能使算法收敛性得以保证。
(2) FZ/T 82006-2018比 FZ/T 73044-2012在内在质量方面多要求考核:湿摩擦色牢度、耐光色牢度和洗后外观。对于一等品,耐汗渍色牢度FZ/T 82006-2018要求更加严格 (高半级)。
非线性变换的目的在于保证二阶矩的存在。实际上,许多非线性变换函数都可以用来抑制α稳定分布尖峰脉冲特性的影响,如对数函数、Sigmoid函数,反正切函数等等。由此产生了利用对数函数的FxlogLMS算法,利用反正切函数的FxatanLMS 算法等等。实验表明,非线性变换后,任意随机过程就具有了有界二阶矩。这样,就可以在自适应过程中采用基于二阶统计量的算法[10]。实验证明FxatanLMS 算法不需设定阀值,稳定性较好,但收敛速率存在问题。FxlogLMS算法存在一段死区,计算量大,限制了它的广泛应用。
2.4 FXSIGMOIDLMS 算法的推导
Sigmoid函数是一个非线性连续函数,其形状如“S”,下面我们提出一种新的基于Sigmoid函数非线性S型转换FXSIGMOIDLMS算法,其代价函数为:

S型函数是单调、奇对称有界函数,g(x)的极限为1,g(x)的方差表示如下:
var[g(x)]=E[(g(x)-E(g(x))2]<1
由此可见,S型转换误差信号方差是有界的,代价函数不依赖于α,因此,不需要先验知识或选择参数α,也无需通过离线统计估测阀值。和FXLMS算法相似,能得出代价函数J(n)相对于滤波器系数矢量梯度为


δ(e(n))x′(n)
其中:
因此,基于FXSIGMOIDLMS算法相应滤波器系数更新等式为
w(n+1)=w(n)-μδ(e(n))x′(n)
2.5 FXSIGMOIDLMS 算法收敛性
脉冲噪声因具有高尖峰特性而幅值过大,Sigmoid 型函数具有饱和的非线性特性,采用基于Sigmoid函数的非线性变换算法对脉冲噪声信号进行预处理,嵌位远离中央位置的高尖峰幅值样本点,约束了脉冲噪声信号幅值,解决了系统稳定性问题。ANR计算机仿真曲线如图5所示。
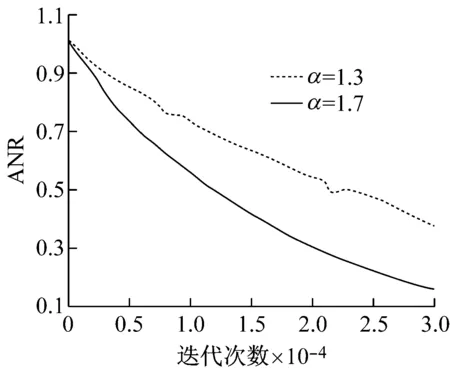
图5 ANR 曲线图
从图5可以看出,本文提出的算法收到了令人满意的收敛速度。不需要事先估测阀值,且算法可进行连续更新,有较好的快速性。可有效抑制脉冲噪声,保证较快的收敛性能[11-12]。
2.6 FXSIGMOIDLMS 算法与FXlogLMS算法比较
α稳定分布具有无界的二阶矩却有有界的对数阶矩。依据此特性,FXlogLMS代价函数表示为
J(n)=E[log2|e(n)|)]≈log2(|e(n)|)
基于FXlogLMS算法相应滤波器系数更新等式为
W(n+1)=W(n)+μsign(e(n))×
(log(|e(n)|))/|e(n)|[s∧(n)*x(n)]=
W(n)+β(e(n))e(n)x′(n)
可以看出,FXlogLMS算法对于处理高尖峰脉冲噪声信号比较有效,实验证明算法稳定性良好,不存在估测阀值和事先设定α值的问题,方便应用。但此算法结构比较复杂,计算量较大,当e(n)的绝对值≤1时,e(n)绝对值的对数与e(n)的比值趋近于无穷大。为了避免这种情况发生,通常会处理e(n)的绝对值等于1,使得此比值等于0,这样的特殊处理后,就会损失原有噪声样本部分信息,影响最终噪声控制效果。另一方面,FXlogLMS算法存在一个死区(|e(n)|≤1时),对比而言,FXSIGMOIDLMS 算法以一个连续模式更新滤波器系数,因此,相比FXlogLMS算法,FXSIGMOIDLMS算法具有更好的消噪性能。
3 结 语
本文在Matlab编程环境下,采用FXSIGMOIDLMS 算法进行仿真,并对结果进行分析,验证算法的有效性。采用不同的算法,根据在Matlab编程环境下仿真结果,对相关算法进行了比较。
从仿真结果可以看出,该算法具有良好的收敛性和稳定性,实际上,FXSIGMOIDLMS 算法从本质上来说是一种等变量步长的FXLMS算法,对于脉冲噪声具有更好的鲁棒性,避免了参数选择和估计阀值的麻烦,更适用于实际应用。下一步预想是根据Sigmoid函数表达式,进一步实验统计分析m值与α值的最佳匹配关系[13-15]。
[1] Priya Thanigai, Sen M Kuo, Ravi Yenduri. Nonlinear Active Noise Control for Infant Incubators in Neo-Natal Intensive Care Units[J].Proc IEEE ICASSP, 2007:109-112.
[2] Akhtar M T,Mitsuhashi W.Improving performance of FxLMS algorithm for active noise control of impulsive noise[J]. Journal of Sound and Vibration,2009,327 (3-5) :647-656.
[3] Lifu Wu, Hongsen He, Xiaojun Qiu, An active impulsive noise control algorithm with logarithmic transformation[J]. IEEE Trans on Audio, Speech and language processing,2011,19(4):1041-1044.
[4] Zhou Y L, Zhang Q Z, Li X D,etal.On the use of an SPSA-based model-free feedback controller in active noise control for periodic disturbances in a duct[J].Journal of Sound and Vibration,2008,317(3-5):456-472.
[5] 周亚丽,张奇志,邵 俊.冲击噪声的有源控制方法综述[J].北京信息科技大学学报,2011,26(5):33-38.
ZHOU Ya-li,ZHANG Qi-zhi,SHAO Jun.A review on active control methods of impulsive noise[J].Journal of Beijing Information Science and Technology University,2011,26(5):33-38.
[6] Gonzalez J G,Paredes J L,Arce G R. Zero-order statistics:a mathematical framework for the processing and characterization of very impulsive signals[J]. IEEE Trans Signal Process, 2006,54(10) : 3839- 3851.
[7] 宋秀丽,尤庆伟,夏 杰.脉冲噪声对工人听力影响的观察[J]. 河南预防医学杂志, 2008,19 (6):418-419.
SONG Xiu-Li,YOU Qing-Wei, XIA Jie.The Observatio on Effects of Impulse Noise on Workers' Listening Ability[J]. Henan Journal of Preventive Medicine,2008,19 (6):418-419.
[8] 邵 俊,周亚丽,张奇志.有源脉冲噪声控制的反正切变换算法[J].噪声与振动控制,2012(2):27-31.
SHAO Jun, ZHOU Ya-li, Zhang Qi-zhi. Arc-tangent Transformation Algorithm for Active Impulsive Noise Control[J]. Noise and Vibration Control,2012(2):27-31.
[9] 周亚丽,张奇志.一种基于非线性变换的脉冲噪声有源控制算法[J].北京信息科技大学学报,2012,27(5):25-28.
ZHOU Ya-li,ZHANG Qi-zhi.Active control of impulsive noise based on a nonlinear transformation algorithm[J].Journal of Beijing Information Science and Technology University,2012,27(5):25-28.
[10] 邱天爽,张旭秀.统计信号处理-非高斯信号处理及其应用[M].北京:电子工业出版社,2004.
[11] 陈克安.有源噪声控制[M].北京:国防工业出版社,2003.
[12] 肖椽生,徐 健,李晓东.虚拟传声器在有源抗噪声护听器的应用[J].声学学报,2010,35( 2) : 140-145.
XIAO Chuan-sheng,XU Jian, LI Xiao-dong.Application of virtual microphone in active noise reduction headset[J].Acta Acustica.2010,35(2):140-145.
[13] Bien Z,Xu J X.Iterative learning control-Analysis, Design, Integration and Applications[M]. Kluwer Academic Publishs,1998.
[14] Zhou Y L,Zhang Q Z,Li X D,etal. Analysis and DSP implementation of an ANC system using a filtered-error neural network[J].Journal of Sound and Vibration,2005,285( 1- 2) : 1-25.
[15] Heinzinger G, Fenwick D, Paden B Miyazaki F. Stability of learning control with disturbances and uncertain Initial conditions[J]. IEEE Transactions on Automatic Control,1992,37(1):110-114.

