基于二阶压控电路的互补型四阶压控滤波器

刘红周, 吴 清, 崔 立, 周 斐, 葛一敏, 谢能达

(华东理工大学 机械与动力工程学院， 上海 200237)

0 引 言

常见的滤波器类型有巴特沃斯滤波器和切比雪夫响应滤波器等[1-2]。这些滤波器各有特点和优缺点，如巴特沃斯滤波器输出在通带很平缓，但当阶数低时，幅频特性输出曲线在通带下降过早[3]。再如Ⅰ型切比雪夫滤波器输出阻带下降快，但在通带有波纹[3-5]。实际中根据需要选择不同性能的滤波器。本文以二阶压控电路为基础进行滤波器的改进设计。

1 互补型滤波器的原理

1.1 二阶压控电路

本文设计的滤波器是以二阶压控电路为基础，电路原理参见图1[6]。它由两节RC电路串联(R1C1和R2C2)和一节放大电路(R3R4)组成，其中同相放大环节的放大倍数即为滤波器的通带增益AF，即：AF=1+R4/R3[7]。由图1：当R1=R2=R，C1=C2=C时，根据基尔霍夫定律可以推导出滤波器归一化的传递函数[6,8]为：

H(s)=AF/[s2+(3-AF)s+1]

其中，s=j(ω/ω0)[6]。

图1 二阶压控电路原理图

1.2 二阶压控滤波器的传输特性分析

由归一化传递函数H(s)可以推导出该系统的幅频输出函数为：

A(x)=|H(s)|/AF=

式中：x=ω/ω0,x是无量纲频率或归一化频率[5]，ω0为截止角频率。为使系统稳定，通带增益AF必须小于3,所以1≤AF<3,暂定AF=2。绘出滤波器的幅频特性曲线，如图2所示。由图可以看出,在通频带，输出曲线并不平滑，而是有一凸峰,这样的滤波效果并不理想，会引起通频带信号的失真。在通频带，理想的情况是A(x)=1，当A(x)>1时，过盈失真；A(x)<1时，则产生不足失真。图3为通过改变增益AF观察到的曲线的变化趋势,图中各曲线对应AF的系列值分别为：1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2。从图3可看出，当AF≈1.6，输出曲线通带最平滑，但AF=0.5ω0A(x)快速下降，产生不足失真;当AF>1.6时，A(x)开始出现过盈失真并随AF增大而增大；AF<1.6时,则出现严重的不足失真。以上两种情况中，过大的过盈失真和不足失真都会使原始信号在通频带产生较大失真，这不是我们希望的。但如果转化思路，将这两缺陷结合起来，让它们形成互补，是否可以得到效果更好的滤波器呢？

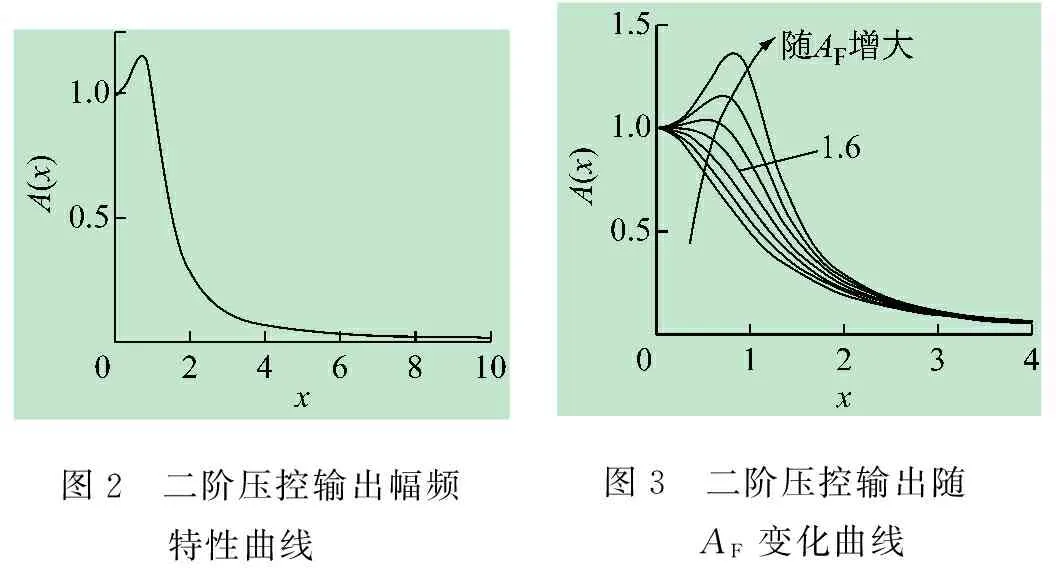
图2 二阶压控输出幅频特性曲线 图3 二阶压控输出随 AF变化曲线

1.3 互补型四阶压控滤波器

本文构造一个四阶压控滤波系统，如图4所示。图中，最后一个同相增益环节1/(AF1AF2)是为了平衡前两个环节的增益系数AF1和AF2。写出它的归一化传递函数为：

图4 四阶压控滤波系统原理图

H(s)=[(s2+(3-AF1)s+1)×

(s2+(3-AF2)s+1)]-1

A(x)={[(1-x2)2+(3-AF1)2x2]×

[(1-x2)2+(3-AF2)2x2]}-1

AF1和AF2分别有一系列的取值，对应着不同的输出幅频特性。经过试验，AF1=1,AF2=2.4是一组便于计算且效果较好的取值组合。此时，A(x)-x的图像如图5所示。

图5 滤波器幅频特性输出图

1.4 四阶互补压控滤波器性能(优缺点分析)

在A(x)表达式中，令A(x)=0.707,解得x=1.07,所以滤波器的截止频率不是ω0而是ωf=1.07ω0,比ω0稍大。由A(x)图像看出，通带中存在波纹，这点是该滤波器的缺陷。当AF1=1,AF2=2.4时，波纹较小，最大波纹处：A(x)max=1.02，即通带有2%的波纹。而它的优点，可以将它与四阶巴特沃斯滤波器和四阶切比雪夫滤波器作对比来说明，具体如下：

(1) 与巴特沃斯滤波器对比。巴特沃斯低通响应是最平坦的响应[5]，它能够最大化滤波器的通带平坦度[3],然后慢慢衰减，这是它的优点。但巴特沃斯滤波器在通带内幅度特性是单调下降的，如果阶次一定，则在靠近截止频率处，幅度下降很多[2]，即通带衰减的过早，这是它的缺陷。四阶巴特沃斯传递函数[9-11]为：

绘出它与本文滤波器的幅频输出对比，见图6。可以看出，同是四阶滤波器，本文滤波器的衰减比巴特沃斯滤波器的晚。为了更准确地对比描述，考虑到两种滤波器在阻带的性能基本相同，着重分析通带的情况，见图6(b)。假设在通带可以接受的最大波动程度是±2%，那在图中，纵坐标0.98就是函数下降的临界值，低于它就可以看做不足失真；与其对应的横坐标为x0，0～x0称为复现带宽。从图6(b)可以看出，巴特沃斯滤波器的复现带宽大小为0.68，四阶互补型滤波器为0.88，可见四阶互补相比于四阶巴特沃斯在通带复现带宽上有所提升，而且衰减得慢。另外,也可以看出，在x取值大于0.68的区间内，A(x)|互补>A(x)|巴特活斯，即互补型滤波器比巴特沃斯滤波器在通带的信号失真要少。

(a) 对比图

(b) 通带放大图

(2) 与切比雪夫滤波器对比。切比雪夫滤波器也是一种常用的滤波器，它的特点是在过渡带比巴特沃斯滤波器的衰减快，但在通频带内存在幅度波动，幅频特性不如后者平坦[5]。所以它的缺陷和本文的互补型滤波器是一样的。第一类切比雪夫滤波器的平方幅频响应表达式[5,14]为：

N=4时的切比雪夫多项式:

T4(Ω)=8x4-8x2+1

将四阶切比雪夫滤波器和本文四阶互补滤波器幅频输出作对比，如图7所示。

图中的切比雪夫滤波器的通带波纹也为2%(ε=0.2)。从图中可以看出，同为四阶，互补型滤波器相比切比雪夫滤波器在滤波性能上大致相同。但本文互补型滤波器在原理及电路结构上比较简单，所以设计起来比较方便。

1.5 滤波器参数的选择

由图1可知，二阶压控电路的参数主要有两级RC电路中的R1、R2和C1、C2与放大电路的R3和R4。其中，为了方便设计和计算，取R1=R2=R，C1=C2=C，具体值可由截止角频率公式ωf=1.07ω0和ω0=1/RC确定。需要注意的是，所取电容值不宜过小，否则容易受杂散电容影响导致电路工作不稳定[6]。而R3和R4则跟通带增益AF有关，可根据AF=1+R4/R3来确定。如图8中所示，滤波器由两级二阶压控电路组成，一级电路中，假设截止频率f0=1.07 Hz，可求出R1=R2=16 kΩ,C1=C2=10 μF。两级电路中参数的不同之处就在通带增益AF上，其他参数均相同。所以R3=R4=R1=R2,C3=C4=C1=C2。AF1=1,AF2=2.4时效果最好，此时对于波纹为2%。所以一级放大电路不需要电阻；二级电路放大环节中，R6=10 kΩ,R7=14 kΩ,AF2=1+R7/R6=2.4。最后，再加一级比例缩小电路R8和R9，来平衡前两个环节的增益系数AF1和AF2。

图7 四阶互补与切比雪夫滤波器输出对比

2 电路实现与仿真

为了验证滤波器的可行性，在仿真软件Multisim中做了仿真，如图8所示。

运放选用LM358。参数选择：R1=R2=R3=R4=16 kΩ,C1=C2=C3=C4=10 μF。截止频率f0=1.07/2πRC=1.07 Hz。一级二阶压控电路放大倍数AF1=1，二级电路AF2=1+R9/R5=2.4。采集信号从Input输入，滤波信号从Output输出。实验源数据采集自齿轮箱转动的轴心位移数据，仿真结果如图9所示。可以看出，该电路是有很好地滤波效果的。

图8 四阶互补滤波器实现电路

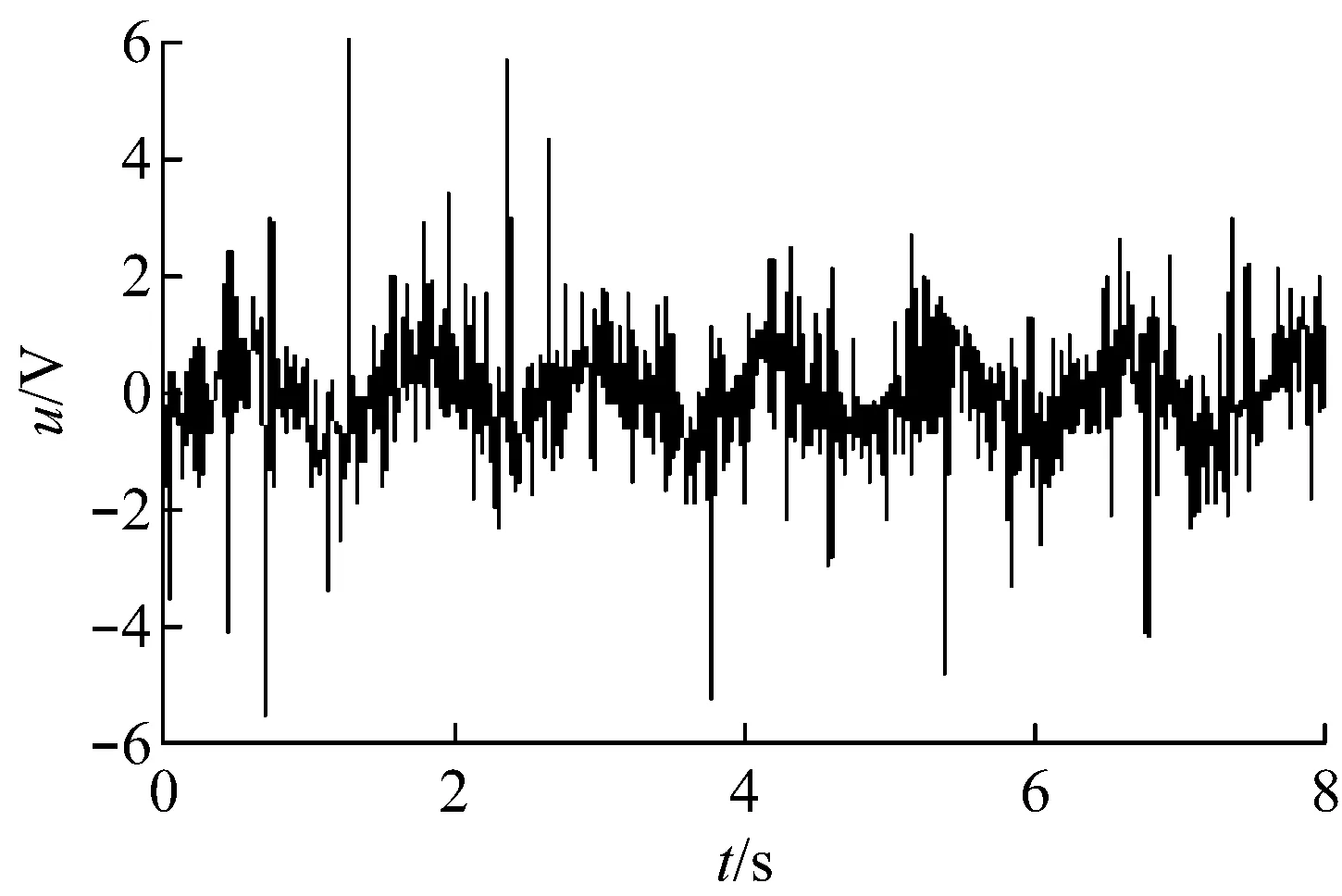
(a) 源数据

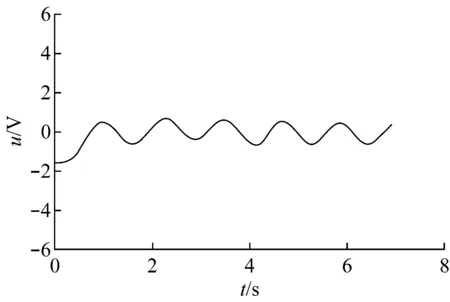
(b) 滤波输出

图9 滤波结果对比图

3 结 语

本文改进设计了一种新型四阶互补型滤波器。相比同样阶数的其他滤波器如巴特沃斯，通带复现带宽提升了14%(波纹2%的情况下)，与同阶数切比雪夫滤波器的性能大致相同，但原理及电路结构较切比雪夫滤波器简单[15]。因此它具有通道内复现带宽大、输出衰减延迟、通带信号衰减较少、原理简单、设计简便的优点。考虑到通带的纹波，此方法适用于允许通带输出有小幅波动的情况中。本文滤波器电路设计简单、方便，设计时两通带增益取AF1=1,AF2=2.4，只要根据截止频率计算出R和C即可完成设计，实际中有一定的参考价值。

[1] 周学军. 基于Matlab的模拟滤波器设计与仿真 [J].现代电子技术,2010,33(8)：62-66.

ZHOU Xue-jun.Design and Simulation of Analog Filter Based on Matlab [J].Modern Electronics Technique.2010,33(8)：62-66.

[2] 贾书圣. 模拟电子线路:线性部分[M].北京：北京理工大学出版社,1996.

[3] 李钟慎. 基于Matlab设计巴特沃斯低通滤波器 [J].信息技术， 2003,27(3)：49-52.

LI Zhong-shen. The Design of Butterworth Lowpass Filter Based on Matlab [J].Information Technology, 2003,27(3)：49-52.

[4] 陶国彬,张秀艳,任玉霞. FIR滤波器的等波纹最优化设计 [J].大庆石油学院学报 2007,31(6)：105-111.

TAO Guo-bing,ZHANG Xiu-yan,REN Yu-xia. Equiripple Optimization Design of FIR filter [J]. Journal of Daqing Petroleum Institute 2007,31(6)：105-111.

[5] Arthur B Williams, Fred J Taylor. 电子滤波器设计[M].宁彦卿，姚金科译.北京：科学出版社，2008.

[6] 高明甫,杨 勇,孔令斌. 二阶压控电压源低通滤波器设计 [J].电子技术,2010,47(3)：73-74.

GAO Ming-fu,YANG Yong,KONG Ling-bin. Design of Low-pass Filter of Second-order Voltage-controlled Voltage Source [J].Electronic Technology, 2010,47(3)：73-74.

[7] 康华光. 电子技术基础模拟部分 [M].4版. 北京:高等教育出版社,1999.

[8] 杨 勇,邢 磊,诸远奇,等. 压控电压源2n阶单位增益巴特沃斯低通滤波器优化设计 [J].电子学报, 2011,39(8)：1894-1897.

YANG Yong,XING Lei,ZHU Yuan-qi,etal. Optimal Design of 2nth-Order Voltage-Controlled Voltage Source Unit Gain Butterworth Low-Pass Filter [J]. Acta Electronica Sinica, 2011,39(8)：1894-1897.

[9] 刘小群. 基于Multisim的四阶有源低通滤波器的设计与仿真 [J].新技术新工艺, 2011(6)：35-36.

LIU Xiao-qun. Design and Simulation of 4nd Source Low-passed Filter based on Multisim [J]. New Technology & New Process, 2011(6)：35-36.

[10] 熊 健,王福明. 基于开关电容技术的巴特沃斯滤波器设计及PSpice仿真研究 [J].现代电子技术, 2007,30(23)：174-175.

XIONG Jian,WANG Fu-ming. Design of Butterworth Filter Based on Switch- Capacitance and Its PSpice Simulation [J]. Modern Electronics Technique, 2007,30(23)：174-175.

[11] 张维玺. 巴特沃斯数字陷波滤波器的设计 [J].现代电子技术, 2008,31(18)：129-131.

ZHANG Wei-xi. Design of Digital Butterworth Notch Filters [J]. Modern Electronics Technique, 2008,31(18)：129-131.

[12] 吴小役,李长红,靳小军,等. 切比雪夫滤波器在PMSM伺服系统中的应用 [J].电力电子技术, 2006,40(1)：73-75.

WU Xiao-yi,LI Chang-hong,JIN Xiao-jun,etal. Application of Chebyshev Filter in the PMSM Servo System [J]. Power Electronics, 2006,40(1)：73-75.

[13] 陈俊吉, 张保平. 广义切比雪夫滤波器耦合矩阵的优化 [J].科学技术与工程, 2010,10(8)：1981-1984.

CHEN Jun-ji,ZHANG Bao-ping. Optimization of the Coupling Matrix for Generalized Chebyshev Filter [J]. Science Technology and Engineering, 2010,10(8)：1981-1984.

[14] 李静洁,吴 康. 关于切比雪夫递推方程组的若干研究 [J]. 汕头大学学报：自然科学版, 2012,27(1)：5-9.

LI Jing-jie,WU Kang. Study on Tschebyscheff Recursive Equations [J]. Journal of Shantou University(Natural Science Edition), 2012,27(1)：5-9.

[15] 王一凡,贾宝富,罗正祥. 广义切比雪夫滤波器等效电路参数的提取 [J].真空电子技术, 2007(1)：8-10.

WANG Yi-fan, JIA Bao-fu, LUO Zheng-xiang. The Extraction of Equivalent Circuit Parameters for General Chebyshev Filter [J]. Vacuum Electronics, 2007(1)：8-10.