基于长期强度的节理岩体洞室蠕变特性研究*

于超云，唐春安

(大连理工大学岩石破裂与失稳研究中心，辽宁大连116024)

岩石在地层长期的沉积、胶结和褶皱等地质运动中，产生了大量的层理、节理、裂隙、断层和破碎带等软弱结构面，这些结构面的存在极大地影响了岩体的力学性态。在岩石工程中，如岩质边坡、煤矿巷道、岩基等工程，节理岩体的强度、变形和破坏特性常常具有显著的时间效应。在岩石力学中，岩石在力的作用下发生与时间相关的变形的性质，称为岩石的流变性［1］。作为岩石流变特性之一，岩石的蠕变特性与工程的稳定性和耐久性有着密不可分的关系。因此，研究节理发育的岩体的流变特性具有一定的工程实践意义。

近年来，国内外进行了大量节理岩体的室内试验和现场量测，并提出了许多模拟节理岩体蠕变特性的力学模型和计算方法。孙钧院士等［2］探讨了多组节理岩体的剪切变形规律、各向异性性态及其时间效应，并用砂岩-泥岩弱面进行的弱面流剪试验验证了对节理面采用弹粘塑性的力学模型的正确性。熊良霄、杨林德［3］采用fish语言对FLAC-3D软件中的interface单元进行修正，将模型单元的法向刚度和切向刚度转化为时间的蠕变函数，建立了考虑节理法向蠕变的节理岩体蠕变模型。目前对于节理岩体的流变特性研究，无论是理论模型研究还是数值计算方面都是以弹粘性或弹粘塑性为理论基础的［4-5］，但是从细观弹脆性本构的角度研究节理发育岩体的流变特性的案例较为少见。

本文从细观角度出发，采用考虑岩石长期强度的岩石破裂过程分析系统对节理岩体洞室在恒定荷载作用下围岩的破坏过程进行数值试验研究，分别考虑了节理角度、节理间距等因素对节理发育岩体洞室围岩蠕变特性的影响。通过这些研究，以期揭示岩石蠕变的本质，并能为岩石工程的稳定性等研究提供一些参考依据。

1 细观单元蠕变损伤模型

1.1 细观单元的本构模型

岩石破裂过程分析系统(RFPA)是唐春安教授团队研发的一款以弹性力学为应力分析工具、以弹性损伤理论及其修正后的Coulomb破坏准则为介质变形和破坏分析模块，以模拟材料渐进破裂直至失稳全过程为特色的新型数值实验工具。唐春安等［6］认为细观非均匀性是造成准脆性材料宏观非线性的根本原因，并认为岩石介质基元的破裂性质在细观层次上表现为弹脆性的，而非塑形行为。因此，在RFPA系统中，近似地假定岩石的基元介质在破坏前的本构关系用线弹性性质描述。细观单元弹性本构模型［7］见图1。

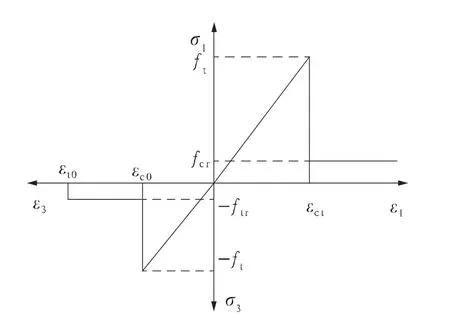
图1 细观单元弹性本构模型

在RFPA系统中［7］，假定岩石的基元介质在破坏前的力学性质用线弹性性质来描述，并且将岩石在细观层次上的破坏分为拉伸和剪切破坏(压缩和剪切应力作用下)。当单元处于拉伸状态时，运用最大拉应力(应变)准则判断拉伸破坏的情形(见式1)。当细观单元产生拉伸损伤时，相应的损伤变量(见式2)。

式中:ft为单轴抗拉强度;ftr为抗拉残余强度;εt0为最大拉应变;εtu为极限拉应变。

当单元承受的剪应力超过其能承受的最大剪应力时，用摩尔-库伦准则判断剪切破坏的情况。

此时的力学损伤变量定义如下:

式中:φ为内摩擦角;fc为单轴抗压强度;fcr为抗压残余强度;εc0为最大压应变。

1.2 考虑长期强度的蠕变损伤模型

岩石的长期强度对工程建筑物，如地下洞室、边坡、坝基稳定等设计有着重要的现实意义，因此，长期强度一直是工程技术人员和科研人员关注的重点问题［8-9］。一般情况下，当荷载达到岩石的峰值强度(通常指岩石单轴抗压强度)时，岩石发生破坏。在岩石承受荷载低于其峰值强度的情况下，如持续作用较长时间，由于流变作用，岩石也可能发生破坏。因此，岩石的强度是随外载作用时间的延长而降低，通常把作用时间t→∞时强度(最低值)σ∞称为岩石的流变长期强度［10］。李连崇等［11］考虑岩石损伤过程的时间因素影响，在岩石破裂过程分析系统(RFPA)的基础上，借鉴瞬时强度和长期强度的概念，通过引入岩石细观单元蠕变本构方程［12］，把长期强度引入到模型单元的应力计算中，建立了考虑流变效应的岩石破裂过程蠕变损伤数值模型，并对恒定载荷作用下岩石蠕变破坏过程进行了数值模拟。

通过长期荷载破坏试验确定的岩石长期强度曲线可以用指数型经验公式表示:

由式(5)可知，由t=0时，σt=A+B;由t趋于无穷时，σt趋于σ∞，得σ∞=A;故得B=σt-A=σ0-σ∞。为表述方便，将长期强度与瞬时强度的比值定义为β，即β=σ∞/σ0，因此可以将细观单元的蠕变损伤本构方程改写成:

式中:σ0为岩石材料细观单元体的瞬时抗压强度;σ∞为岩石材料细观单元体的长期强度;α为由试验确定的岩石细观单元强度衰减系数。β为长期强度与瞬时强度之比。根据目前经验资料，对于大多数岩石，长期强度与瞬时强度之比β为0.4～0.8［10］。图2为岩石细观单元蠕变本构关系曲线示意图［12］。

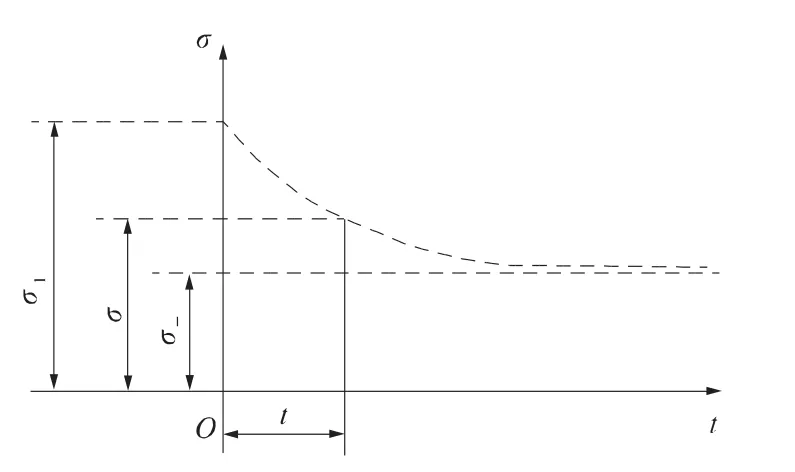
图2 岩石细观单元蠕变本构关系曲线

2 单轴压缩蠕变的数值试验

2.1 数值模型及其参数

为了分析节理间距和节理夹角对岩体蠕变特性及其破坏特征的影响，建立采用如图3所示的数值模型，其中，d为节理间距，θ为节理与水平面的夹角，而两组节理的夹角为2θ。本文讨论了节理间距分别为2 m、3 m、4 m以及节理水平夹角分别为20°、30°、45°、60°、70°等几种情况。模型尺寸均为100 m×100 m，将模型划分为300×300(90 000)个单元。在竖直方向上施加4 MPa的恒定载荷，底部固定，无围压。在模型中，开挖一个半径为5 m的圆形洞室。模型中的A点作为预定测量的隧洞变形量的点，位于洞室底部中点。表1给出了模型中其他物理力学性质参数。

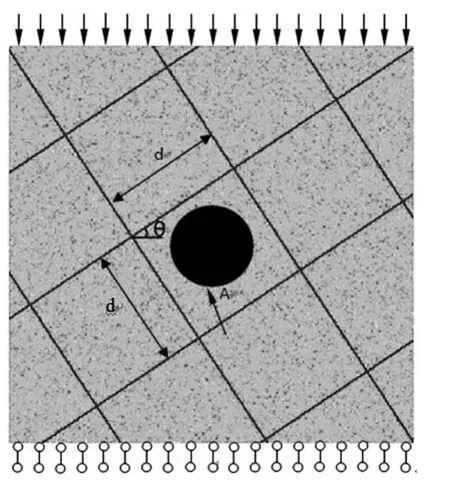
图3 数值模型示意图

2.2 围岩破坏分析

经分析，不同工况下的围岩破坏形态具有相似性，因此以节理间距为3 m，水平夹角为20°的情况为例，分析其蠕变破坏的过程。图4给出了该洞室在恒定荷载作用下随时间变化的破坏过程。在开挖初期，由于开挖破坏了岩体原有的应力平衡状态，围岩应力进行重新分布，从图中可以看出，洞壁左右两侧应力集中现象明显，随着时间的增长，应力集中的范围有扩大的趋势。另外，在洞顶和洞底的一定深度范围内，出现了应力松弛区(图中深色部位)。考虑到长期强度的影响，当集中应力值大于或者等于随时间衰减后的强度时，围岩就会发生破坏。首先，破坏出现在应力集中较为明显的洞壁两侧围岩的位置，破坏范围小且密集但没有宏观裂纹的出现。随后，洞底和洞顶的位置也出现了微裂纹，并且裂纹尖端应力集中，加之应力松弛区的存在，导致了微裂纹向深部围岩的扩展、演化直至形成了宏观裂纹。由此可以得到的是节理岩体洞室的蠕变是一个岩石内部损伤随时间积累由量变到质变的过程。

表1 节理岩体洞室模型细观力学参数

2.3 影响节理岩体蠕变特性的因素

图5是数值模拟得到的隧洞A点在相同节理水平夹角不同间距的情况下的单轴蠕变特性曲线。从A点的蠕变曲线中可以看出，随着节理间距的增大，衰减蠕变段的曲率半径减小，而衰减蠕变段的曲率半径直接影响到节理岩体达到稳定蠕变阶段的时间，即节理岩石蠕变进入稳定蠕变阶段所需的时间将缩短。此外，随着节理间距的增大，初始蠕变加载瞬时应变量减小，由间距2 m的5.609 mε减小到3m的5.47 mε再变到4 m时的5.37 mε，并且最终都达到稳定蠕变阶段，同样的，稳定阶段的应变量也是随着节理间距的增大而减小。

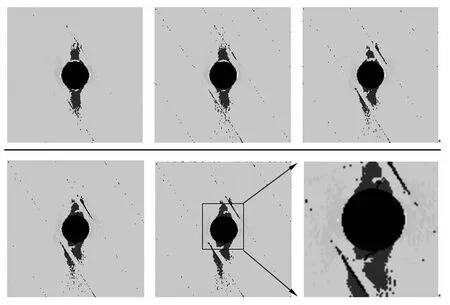
图4 节理间距为30 mm、水平夹角为20°时破坏过程

图6给出了相同节理间距不同水平夹角情况下的蠕变特性曲线。从图6中可以看出，当水平夹角小于45°时，随着夹角的增大，节理岩体的蠕变特性将会增强。反之，当水平夹角大于45°时，随着夹角的增大，蠕变特性减弱。当水平夹角为45°时，蠕变特性曲线变化最为明显，并且除了衰减蠕变和稳定蠕变之外，还有加速蠕变阶段。另外图6给出了初始蠕变量随着水平夹角的变化趋势图。这与文献［3］的结论是一致的，进一步说明了该理论模型的正确性和合理性。

图5 不同节理间距时岩体的单轴蠕变曲线

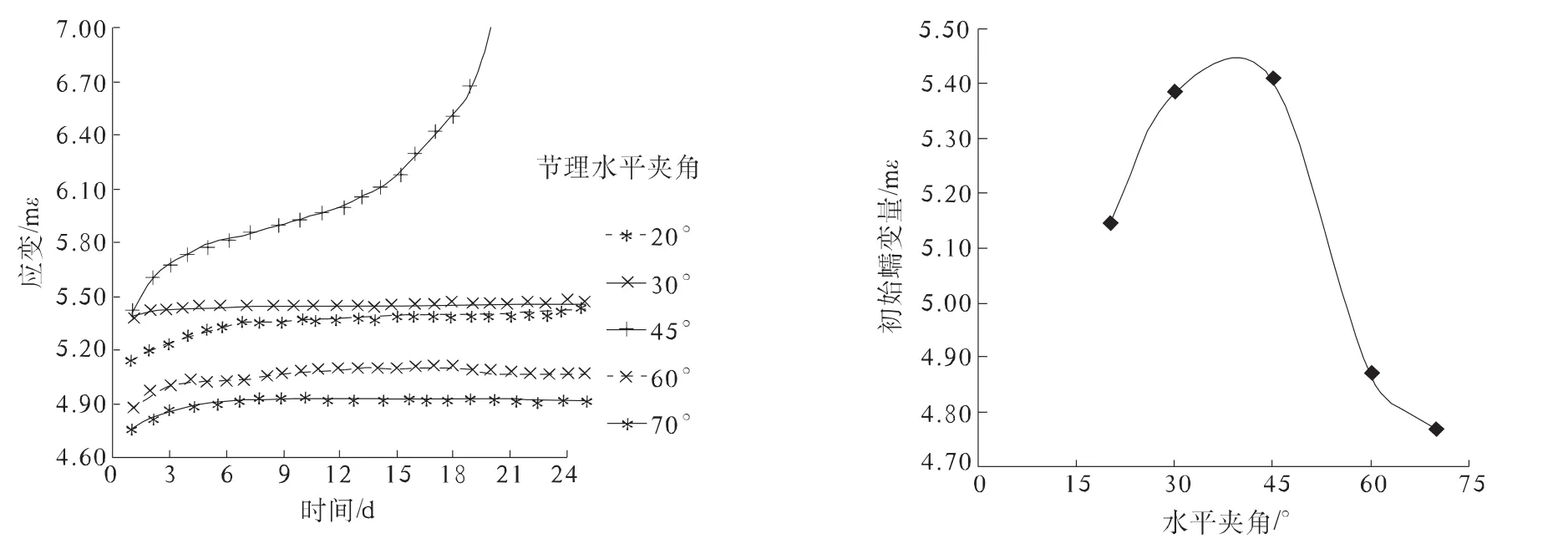
图6 不同节理夹角时岩体的单轴蠕变曲线

3 结论

本文通过对含节理岩体开挖后的破坏过程及围岩的变形等分析，得到了以下结论:

1)RFPA-2D系统所采用的细观单元弹脆行本构关系及简单的破坏准则，适用于岩石类材料的蠕变破坏这一复杂的、非线性演化问题，可以全面描述初始蠕变阶段，稳定蠕变阶段甚至是加速蠕变阶段的蠕变特性。

2)蠕变是一个岩石内部损伤积累的过程，在开挖初期，由于洞室短时间内处在一个恒定荷载作用下，瞬时产生的损伤较大，但是随着时间的延长，内部的损伤趋于减弱，应变率则保持相对稳定的状态，当岩石的力学性质进一步弱化时，内部损伤急剧增加，表现为加速蠕变。

3)节理间距与节理夹角对岩体的单轴蠕变变形有显著的影响。节理间距越大，岩体的蠕变变形越小。当节理面水平夹角小于45°时，夹角越大，蠕变变形越大，当大于45°时，夹角越大，蠕变变形越小当节理面倾角等于45°时，围岩出现大量破坏，并表现出加速蠕变的特征。

［1］孙钧.岩土材料流变及其工程应用［M］.北京:中国建筑工业出版社，1999.

［2］李永盛，孙钧.多组节理岩体洞室的蠕变特性及其粘弹塑性效应［J］.同济大学学报:自然科学版，1986，14(3):281-291.

［3］熊良宵，杨林德.考虑节理面法向蠕变的节理岩体蠕变模型［J］.中南大学学报:自然科学版，2009，40(3):814-821.

［4］陈胜宏，王鸿儒，熊文林.节理岩体的数值分析和模型试验研究［J］.岩土工程学报，1989，11(3):22-30.

［5］杨松林，张建民，黄启平.节理岩体蠕变特性研究［J］.岩土力学，2004，25(8):1225-1228.

［6］Tang C A，Kaiser P K.Numerical simulation of cumulative damage and seismic energy release during brittle rock failure—part I:fundamentals［J］.International Journal of Rock Mechanics and Mining Sciences，1998，35(2):113-121.

［7］唐春安，王述红，傅宇方.岩石破裂过程数值试验［M］.北京:科学出版社，2003.

［8］明可前，吴相超，李维树.岩石的流变特性及其长期强度［C］//重庆岩石力学与工程学会测试与分析专业委员会2000年学术交流会论文集，2000.

［9］张强勇，杨文东，陈芳，等.硬脆性岩石的流变长期强度及细观破裂机制分析研究［J］.岩土工程学报，2011，33(12):1910-1918.

［10］张永兴.岩石力学［M］.北京:中国建筑工业出版社，2004.

［11］蔡美峰，何满潮，刘东燕.岩石力学与工程［M］.北京:科学出版社，2002.

［12］李连崇，徐涛，唐春安，等.单轴压缩下岩石蠕变失稳破坏过程数值模拟［J］.岩土力学，2007，28(9):1978-1986.