基于ZIGBEE的自适应动态区域误差因子算法*

张 是,李德敏,张晓露

(东华大学信息科学与技术学院,上海201620)

基于ZIGBEE的自适应动态区域误差因子算法*

张 是,李德敏,张晓露

(东华大学信息科学与技术学院,上海201620)

为了进一步完善ZigBee定位技术,减少多径效应对室内定位的影响,在接收信号强度指示算法(RSSI)的基础上,提出了一种自适应动态区域误差因子算法,通过将最小二乘法与自适应动态区域误差因子相结合的方法,来计算盲节点的位置坐标,以达到提高定位精度的效果。Matlab中的仿真结果证明,在节点处于静态和动态两种情况下,该算法在定位精度上都有显著的提升。

ZigBee定位 RSSI测距 最小二乘法 自适应动态区域误差因子

0 引 言

近年来,室内定位的问题越来越受业界广泛的关注,随着社会的发展,对定位问题的研究也存在着重大的意义和研究价值。例如在火灾现场、矿灾现场对人员的救援缺乏准确可靠的定位信息,抢险救灾的效率低,成功率小。而利用定位技术能准确地定位到被困人员的具体位置,从而给应急救援争取了宝贵的救援时间,带来了极大的方便,大大的减少伤亡人数。

与此同时,国内外各种相应的定位方式也不断涌现,目前的定位技术主要有红外线室内定位技术、超声波定位技术、蓝牙定位技术、射频识别定位技术等。由于诸如功耗和通信成本等原因,这些技术还没有被广泛的应用。自2006年正式推出ZigBee标准以来,业界提出了不少基于ZigBee技术的定位算法,如三边测量法、三角测量法和最大似然估计定位法。这些方法虽然可以有效减小功耗等带来的问题,但是由于ZigBee无线网络往往受到障碍物的影响而使定位精度很低,所以基于ZigBee的室内定位技术还有待于进一步的完善。

鉴于ZigBee技术其自身低功耗、低成本等特点,能够更好的满足短距离室内定位的要求。为了改善现有的定位技术精度低的问题,文中提出了一种基于ZigBee的自适应动态区域误差因子算法,该算法的设计是在原有接受信号强度指示(RSSI,Received Signal Strength Indicator)定位算法的基础上,通过最小二乘法拟合及动态区域误差因子相结合的方法,来修正盲节点的定位坐标,以达到提高定位精度的效果。

1 相关工作

为了减小室内定位中多径效应对基于RSSI定位算法的影响,国内外的研究人员先后提出了不少的定位算法改进方案,2008年高国胜等人在文献[1]中提出了一种基于RSSI测距的信标节点自校正定位算法,以三边定位算法为基础,通过测量信标节点之间的距离,获得RSSI值的网络定位误差,并对误差进行补偿,从而提高整个网络的定位精度,但三边定位算法本身的误差就较大,因此该算法虽然提出的想法比较新颖,但还有待继续改进。2012年杜亚江等人的文献[2],在基于RSSI的测距技术的基础上,提出使用最小二乘法对环境参数进行拟合的方案,但没考虑到通信距离过长的问题,在这样的条件下测量的RSSI值拟合出的结果会造成不可预见的误差。2013年CHUKU N等人在文献[3]中,在RSSI的阴影模型的基础上,引入了最小二乘法和高斯函数,提高了定位精度,但同时也增加了整个算法的复杂度,使其不适用于有移动节点且内部环境较复杂的室内定位。

由于室内的定位环境相当复杂,如何在考虑到节点能耗,不增加算法复杂度的情况下,提出一个可以符合室内环境的定位算法,已成为如今室内定位中的一大研究难点。文中在文献[1]和文献[3]的基础上提出一种动态区域误差因子定位算法,根据盲节点的位置及接收信号的范围,将定位环境缩减成一个小范围区域,在这个动态变换的区域内计算盲节点的RSSI误差因子,以此来提高整个网络的定位精确度。

2 自适应动态区域误差因子算法

2.1 基于RSSI的路径损耗模型分析

RSSI技术是通过接收到的信号强弱测定信号点与接收点的距离,进而根据相应数据进行定位计算的一种定位技术。之所以要采用动态的有目的有方向性的选择不同参考节点来分别计算移动节点的位置坐标,是因为RSSI技术在复杂的环境中,受障碍物或反射物的影响较大,从而导致测量误差较明显,使得精度很低。

电波在自由空间传播的距离、频率和信号衰减的关系为[4]:

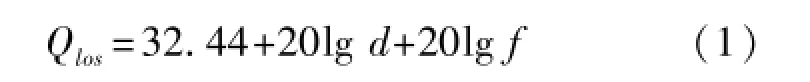
式中,Qlos为传播损耗,单位为dB,d为距离,单位为km,f为工作频率,单位为MHz。

当电波的频率和发射功率固定不变时,通信的距离和接收器接收到的功率直接相关,由于不同的环境下信号的衰减程度不同,在相应的环境下进行测量得到传播损耗经验值,并对式(1)进行修正。

RSSI的理论值可表示为[4]:

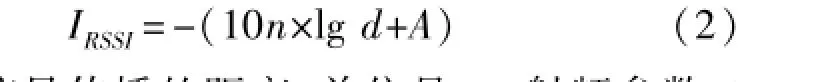
式中,d为信号传播的距离,单位是m,射频参数A和n用于描述网络操作环境。在全向模式下,射频参数A被定义为用dBm,表示的距发射端1 m处接收到的信号强度绝对值。射频参数n被定义为路径损失指数,它指出了信号能量随着到收发器距离的增加而衰减的速率。RSSI的定位原理为已知发射节点的发射信号强度,接收节点根据接收信号的强度,计算出信号的传播损耗,利用理论和经验模型将传输损耗转换为距离,再利用三边测距法计算出节点的位置,因此RSSI定位方法要求多个参考节点。

2.2 最小二乘法原理

为了减小路径损耗模型中三边测距法对于盲节点位置的计算误差,文中将在此基础上再用最小二乘法对盲节点坐标进行进一步的拟合。根据最小二乘法的原理,为了计算得到盲节点的坐标,则盲节点和信标节点之间的位置关系必须满足式(3)[3]取得最小值:

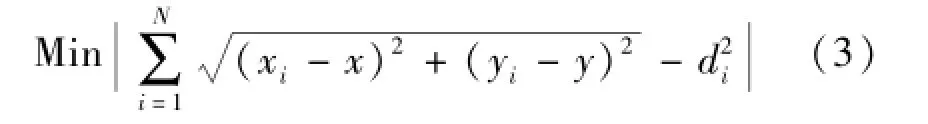
式中,xi,yi是信标节点i的坐标值,di是通过RSSI值计算得到的从盲节点到信标节点i之间的距离,N是总的信标节点的数量。由式(3)可以推导出矩阵形式的式(4):

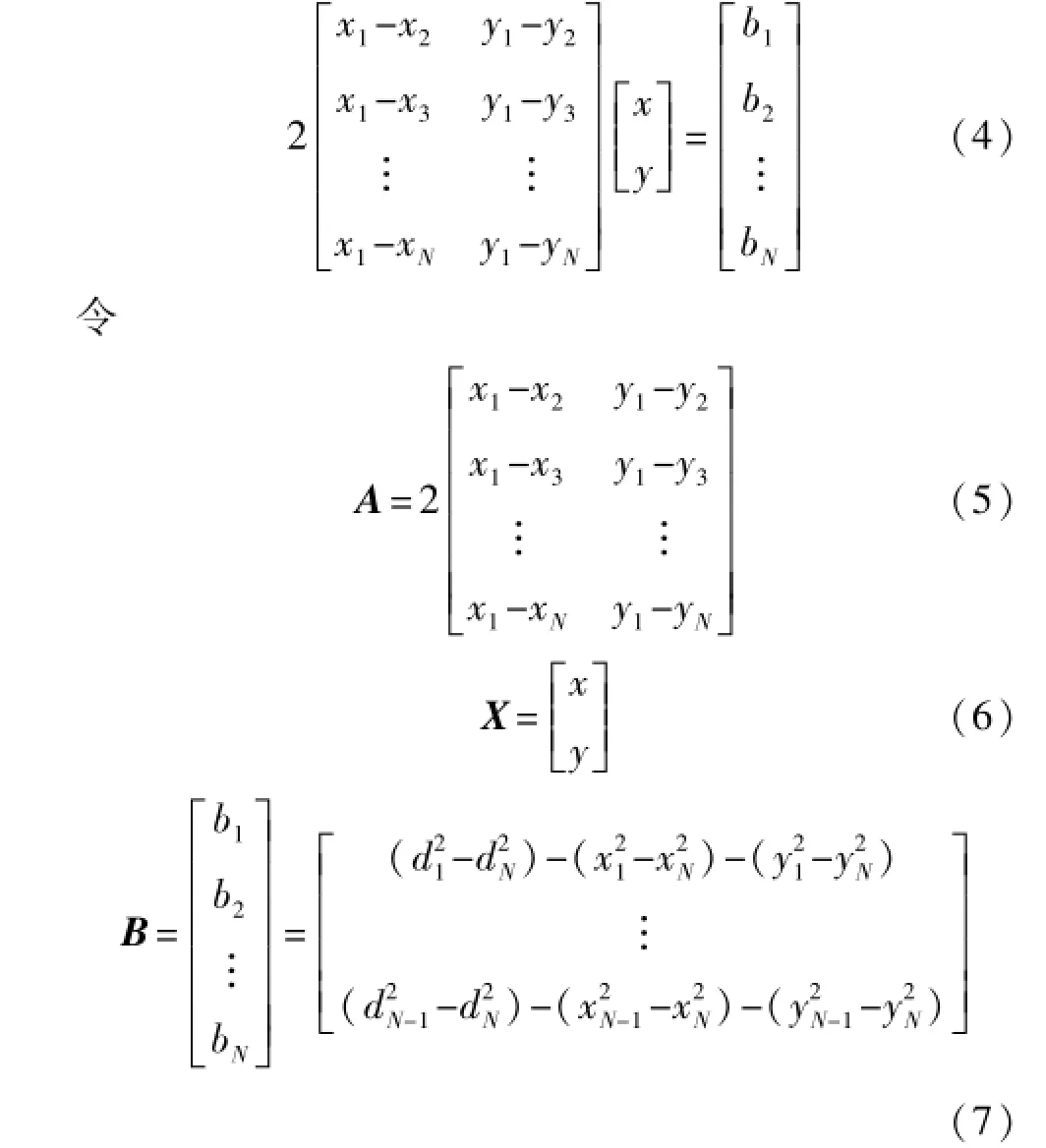
则可以将式(4)简化为:A·X=B,应用最小二乘的原理,只要计算得到P(X)=‖A·X-B‖2的最小值,即能求解得到盲节点的近似坐标:X= (ATA)-1ATB。

2.3 自适应动态区域误差因子算法描述

由于在室内环境的传播过程中,RSSI值的受外界因素影响较大,在使用传统的方式获得节点坐标的基础上,必须针对具体环境,对基于已损耗的RSSI值所计算出的距离进行补偿,以此来提高定位可靠性,因此,文中设计了一种自适应动态区域误差因子算法,可以较为有效的减小外界环境变换所带来的定位误差。

文中所设计的自适应动态区域误差因子算法,主要是使用最小二乘法对RSSI传播模型中所计算出的测距结果进行拟合,在拟合结果的基础上加入了动态的区域误差因子,以减小最小二乘法在使用受过外界干扰的RSSI值后计算出的拟合误差。最后在计算结果上加上的固有环境误差因子,可以有效针对具体定位环境提高定位精度。

2.3.1 动态定位区域确定

当有盲节点加入到整个定位网络时,算法首先需要在局部范围内确定出参与盲节点定位的信标节点,即算法的动态定位区域。

每个盲节点进入到网络时,都会收到来自于周围不同信标节点所发送来的RSSI值信息,由于RSSI值受距离的影响比较大,因此拥有较小RSSI值的节点将会被舍去,而剩下的超过某一阈值η的信标节点的信息将会被列入到集合中,形成信标节点位置坐标集合{(x1,y1),(x2,y2),…,(xN,yN)}及与之对应的RSSI值集合{RSSI1,RSSI2,…,RSSIN},集合中所包括的信标节点,形成了一个动态的相对于每一特定的盲节点的定位区域。

2.3.2 最小二乘法盲节点坐标计算

由于只需要接收到三个信标节点的信息,即可通过最小二乘法计算得出盲节点的坐标,因此,当经过筛选后,在动态定位区域内的信标节点个数大于等于3时,即可通过计算模型计算出C3N个盲节点的近似坐标(x1,y1),(x2,y2),…,(xk,yk),其中k= C3N。在舍去两个极端坐标,再取平均值后,便能够得到盲节点在初级坐标(x,y),如式(8):

2.3.3 自适应动态区域误差因子

由于在传播过程中RSSI值随环境的影响很大,因此使用带有误差的RSSI值计算得到的盲节点坐标本身也会存在很大的定位偏差,为了减小不可抗因素所带来的影响,文中在文献[1]提出的测距校正模型的概念上,引入了一种自适应动态区域误差因子,以此来修正盲节点的坐标。

当一个盲节点进入到网络后,可以通过获得信标节点的信息来计算自身的坐标,同理,已知自身坐标的信标节点也可以通过接收别的信标节点的信息来计算自身的位置坐标,而通过最小二乘法计算得到的坐标与实际的坐标之间的差值,即为在实际环境中的计算误差,在对盲节点的坐标进行计算时,需要将盲节点所处区域的环境误差均值考虑在计算范围内,而此误差均值,即为所引入的自适应动态区域误差因子。

由于RSSI值传输结果的不确定性,在此基础上计算得到的距离中必然会存在小概率事件,文献[5]中提出使用高斯模型处理数据可以有效的避免小概率事件的发生,因此,文中假设所提出的自适应区域误差因子符合高斯分布,得到:

定义1信标节点的自适应动态区域误差因子为:

式中,Dij=deij-dsij,deij为第i个信标节点通过最小二乘法拟合出的与第j个信标节点之间的估计距离, dsij为第i个信标节点与第j个信标节点之间的实际距离,i与j为N个信标节点中的任意两个节点。由此可知,两两信标节点间一共有种距离组合,因此W=。

定义2盲节点修正坐标

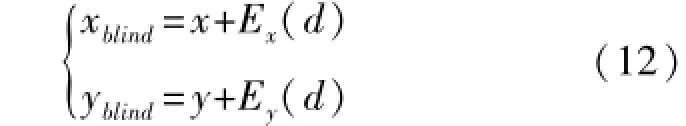
在使用最小二乘法计算得出的坐标基础上加上自适应动态区域误差因子分量,即可求得盲节点的最终定位坐标。

自适应动态区域误差因子算法流程如图1所示。

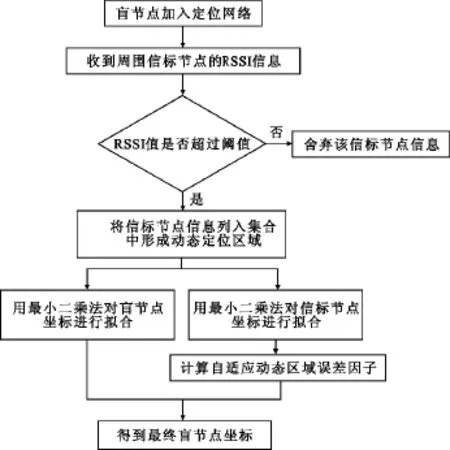
图1 自适应动态区域误差因子算法流程Fig.1 Flow chart of adaptive dynamic regional error factor algorithm

3 算法仿真分析

文中采用了Matlab网络仿真平台对所提出的自适应动态区域误差因子算法以及文献[1]中的信标节点自校正定位算法和文献[3]中的一种基于RSSI的无线传感器网络减轻阴影模型影响的定位方案(RBMSE,An RSSI Based Localization Scheme for WirelessSensorNetworkstoMitigateShadowing Effects)算法进行比较和分析。仿真场景设置为一个50 m×50 m的正方形区域,区域里随机分布100个已知坐标的信标节点,以及25个待定位的盲节点,节点的通信半径均为10 m。

3.1 静态定位仿真

图2为三种算法在不同盲节点数量情况下的平均定位误差仿真图。从仿真结果可以看出,文中所提出的自适应动态区域误差因子算法在静态定位环境下定位误差小,且趋于稳定,另两种算法相较于文中的算法定位误差大,且随着盲节点数量的增多,误差骤增。

图2 静态平均定位误差Fig.2 Static average location error

3.2 动态定位仿真

在上文所提到的基本仿真参数的基础上,假设盲节点的移动速度(m/s)分别为0、0.5、1、1.5、2,即可得出图3中三种算法在动态定位环境下的平均定位误差比较。从图3中可以看出,在节点移动的情况下,三种算法的定位误差明显高于在静态定位环境下的误差值,但文中所提出的算法相较于另两个算法,依然定位效果更佳,平均误差更小更稳定,没有误差骤增的问题,能更加灵活的应用于不同的定位场合。而另两种算法,由于其算法复杂度及算法定位所需时间的问题,使其无法适用于移动节点的定位环境,造成了较大的定位误差,且随着节点移动速度的增大,定位误差成倍增长。

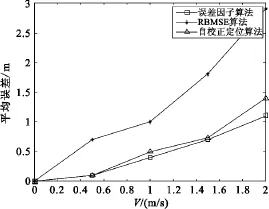
图3 动态平均定位误差Fig.3 Dynamic average location error

4 结 语

针对室内定位环境差定位精度低的问题,文中提出了一种自适应动态区域误差因子算法,通过将最小二乘法与动态区域因子相结合的方法来解决RSSI值在室内复杂环境中衰减大,定位精度不高的问题。文中在Matlab中对静态和动态的两种定位环境进行了仿真,仿真结果证明,文中所提出的算法,定位精度更高,可应用于各种不同的室内定位环境中。

[1] 高国胜,陈俊杰,李刚.基于RSSI测距的信标节点自校正定位算法[J].测控技术,2009,28(08):93-97. GAO G S,CHENG J J,LI G.Beacon Node Self-Tuning

Localization Algorithm based on RSSI[J].Measurement and Control Technology,2009,28(08):93-97.

[2] 杜亚江,高立兵.基于最小二乘法的RSSI测距环境参数修正方案[J].计算机系统应用,2012,21(02):221-224.

DU Y J,GAO L B.RSSI Parameter Calibration Methodbased on the Least Square Algorithm[J].Application of Computer System,2012,21(02):221-224.

[3] CHUKU N,PAL A,NASIPURI A.An RSSI Based Localization Scheme for Wireless Sensor Networks to Mitigate Shadowing Effects[C]//Southeastcon.Jacksonville,FL:IEEE,2013:1-6.

[4] 李建东,郭梯云,邬国扬.移动通信[M].西安:西安电子科技大学出版社,2006.

LI G D,GUO Y T,WU G Y.Mobile Communication [M].Xi'an:Xidian University Press,2006.

[5] 章坚武,张璐,应瑛,等.基于ZigBee的RSSI测距研究[J].传感技术学报,2009,22(02):285-288.

ZHANG J W,ZHANG L,YING Y,et al.Research on Distance Measurement based on RSSI of ZigBee[J].Journal of Transducer Technology,2009,22(02):285-288.

ZHANG Shi(1990-),female,graduate student,mainly engaged in the application of wireless sensor network.

李德敏(1963—),男,博士生导师,主要研究方向为移动计算理论与应用;

LI De-min(1963-),male,doctoral tutor,mainly engaged in mobile computing theory and application.

张晓露(1990—),女,博士,主要研究方向为无线传感网络与应用。

ZHANG Xiao-lu(1990-),female,Ph.D.,mainly engaged in the application of wireless sensor network.

Adaptive Dynamic Regional Error Factor Algorithm based on ZigBee

ZHANG Shi,LI De-min,ZHANG Xiao-lu
(College of Information Science and Technology,Donghua University,Shanghai 201620,China)

In order to further improve the ZigBee positioning technology and reduce the multipath effects on indoor positioning,an adaptive dynamic regional error factor algorithm is proposed on the basis of received signal strength indicator.This algorithm,by combining the least square method with adaptive dynamic area error factor,calculates the coordinates of the blind nodes and thus improves the positioning accuracy.The simulation with Matlab indicates that both the complexity and the positioning accuracy of the algorithm could be significantly improved.

ZigBee positioning;RSSI;least square method;adaptive dynamic regional error factor

TN929.5

A

1002-0802(2014)02-0179-05

10.3969/j.issn.1002-0802.2014.02.012

张 是(1990—),女,硕士,主要研究方向为无线传感网络与应用;

国家自然科学基金资助项目(No.71171045):自组织社会网络的特征信息融合与决策支持方法研究

Foundation Item:National Science Foundation of China(NSFC)(No.71171045)