节点具有相关性的树形结构的验证方法

吴洁明，李硕征，史建宜

（北方工业大学信息工程学院，北京100144）

0 引 言

实际应用中，经常利用树形结构反映现实中的组织结构关系。但是，如果这些组织中的实体之间具有很强的相关性，即各实体之间具有较强的相互影响，那么映射形成的树形结构的各个节点的取值就会也具有相关性。这对进一步应用造成了一定困难。为了解决这一问题，为了解决这个问题，本文提出了一种基于树形结构的验证方法。

树形结构能够很好地反映现实中的某些组织关系，如组织结构等，而且具有便于查询、层级关系清晰等优点［1］。因此在实际应用中，经常将项目的各数据实体或元素（下文中统称为元素）映射成树形结构，各元素映射成树中的各节点。期望可以通过树形机构层级关系清晰的优势，结合增、删、改、查等操作以解决实际问题。然而，在实际应用中经常会遇到符合树形结构的各元素之间具有相关性的情况，即某一个元素是否出现或者取值情况，对其他元素是否出现或取值产生影响。因而，在使用各元素执行进一步操作的之前需要对各元素的正确性及合法性进行验证。

本文提出的这种基于树形结构的验证方法，可以通过验证现实中各实体映射出的树形结构中各节点取值的正确性，进而验证各个元素映射成的树形结构的正确性。文章首先简要介绍了树形结构的部分相关算法，在此基础上对算法进行了详细描述并分析了该算法的时间开销，然后通过一个实例介绍了算法的使用，最后对本文进行了总结和展望。

1 相关研究

作为一种十分重要的数据结构，树型结构可以很方便的反映现实世界的组织结构，因此得到了广泛深入的研究和使用。在数据查找算法中，树形结构具有十分重要的作用。在计算机科学中，查找树是最重要的一类数据结构，是一种具有查找、插入和删除操作的元素集合［1］。除二叉查找树外，B树、AVL树和2－3树等也是这方面研究的重点［2］。

由于树本身就是连通的无回路图，因此可以应用树形结构辅助研究图的问题，例如图的遍历算法、最短路径算法等问题［2］。

在数据挖掘方面，FP＿Growth算法中需要构建FP－tree帮助压缩数据库。FP－Tree蕴涵了目标数据中所有的频繁项集。因此，其后的频繁项集的挖掘只需要将FP－growth算法应用到FP－tree上［3，4］。本文正是借鉴了这种思想，把各元素间的关系映射成树形结构，从而利用树形结构的特点，借鉴已有的对于树形结构的研究成果解决元素相关性验证的问题。

2 预备知识

本文中所指的树形结构的节点相关性，是指在某一个具体的树形结构中，一个节点对其他同级或不同级的节点造成的影响。包括:其他节点是否出现、该节点处的取值变化等。一个节点可以对与其同级的节点、较小层级的节点或较大层级的节点造成影响。本文中涉及的相关性有如下几条说明需要注意。

说明1:树形结构中各节点都或者会对其他节点产生影响或者受其他节点的影响。其中根节点影响所有其子节点的出现情况，叶子节点受其所有祖先节点的影响。

说明2:设xi、xj，是两个节点，若xi的存在情况（或取值）会影响xj的存在情况（或取值），并且xj是比xi层级较高的节点，那么xi不在以xj为根节点的子树上。也就是说，本文提出的验证方法不考虑于输出对输入有反馈存在的情况。

对于实际业务中，数据或元素根据是否会受到其他数据或元素的影响可以分为基本元素和条件元素。其中，基本元素的取值或是否存在不受其他的元素或数据的影响，而条件元素的取值或是否存在则要受到这种影响。此外，实际业务中元素的取值是否可以为空也是需要考虑的情况，通常称之为选择性。根据不同的选择性，可以将元素分为必选元素和可选元素两类［5］。可选元素的取值不可为空，而必选元素的取值则可以为空。

将以上各种情况映射到树形结构中，可以将所有的节点分为基本必备节点、基本可选节点、条件必备节点和条件可选节点四类。对于一棵树来说，只有其根节点是基本节点，而且是基本必备节点，其他各个节点都是条件节点。对于森林来说，每棵树的根节点都是基本必备节点。这是因为，一棵树中至少要有根节点存在，并且可以只有根节点而没有其他节点。

对于节点x，y，节点集合X，Y，x∈X，y∈Y，设D（x）表示节点x存在的充分条件，若对于集合Y中任意一节点y，满足y＝D（x），表示只有在集合Y中各节点存在的情况下，节点x才存在。

设P（x）表示节点x存在的时候能够存在的节点。若对于集合Y中任意一节点y，满足y＝P（x），则节点x存在的情况下，结合Y中的节点y才有可能存在。

由上面两个设定可知，y＝P（D（x））以及P－1（x）＝D（x）。

3 算法描述

因为森林是由多个树组成的，相当于包含一个或多个树的集合，所以只考虑一个树的情况。此外，由于是验证某一树形结构的合法性，则必然会存在一个标准的结构，我们把这个标准结构也表示成树的形式，并称之为标准树。与之相对应的，把需要验证的树形结构称为待测树。

首先，根据标准的组织结构生成标准树。在实际应用中，树形结构通常用于表示组织结构情况，树的节点表示组织中的某一元素。因此生成的标准树中保留节点名称和元素名称相同。这一步中最大的问题在于如何处理条件节点，因为在树的定义中，并没有考虑节点可能为空的情况，而且在实际中各节点的取值也有可能出现变化。我们的解决方法是增加虚节点，将各个可能的取值看作是多个不同的虚节点。此外，若某一节点的取值为空，则认为该节点不存在。例如图1中所示的树中，节点b的取值可能为0和1两种情况，则在b右侧增加一个节点，节点名称不变且新增节点和原节点名称相同，值分别为0和1，如图2所示。通过增加这种虚节点的方式，将标准结构映射成标准树。若待测树中，某一个节点为空，则该节点及以其为根节点的子树不可能存在。这样，将节点取值的问题转化成节点是否为空，即节点是否存在的问题。若图1中的树的节点b的取值为0，则只需要在图2的树形结构中去掉节点b（1）的分支即可。需要注意的是，在生成虚节点的时候，以该节点为根节点的子树也要复制到新的虚节点下面。

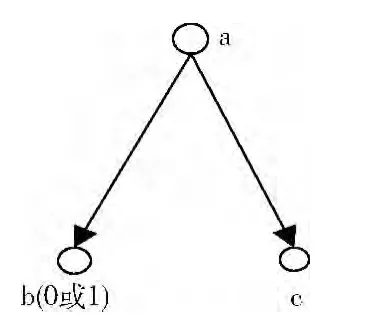
图1 一个简单的树型结构

生成标准树后，按照树的广度优先遍历顺序为标准树中各个节点排序［6－8］，包括上一步生成的虚节点。从根节点开始，自上至下逐层排序；在同一层中按照从左到右的顺序对节点进行排序。这样一来较高层级的节点的序号小于较低层级节点的序号；同一层级中，左侧节点的序号小于右侧节点的序号。设标准树为t，则t＝｛x0，x1，…，xn｝。xi表示树中的节点，n＋1为节点总数，i∈｛0～n｝表示各节点的序号。同时，根据标准情况记录各节点的名称和取值以及各个节点出现的充分条件，即记录节点xi和其对应的D（xi）。

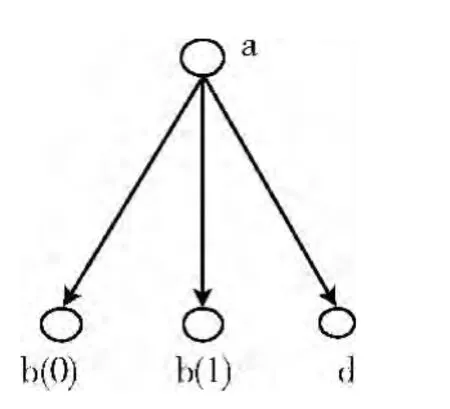
图2 生成虚节点后的树形结构

采用深度优先遍历的方法，遍历标准树和待测树。在此过程中，通过节点名称，验证各个节点的父节点是否正确。由于待测树和标准树在实际应用中，应该表示的是同一组织结构，因此，待测树和标准树中对应节点的名称应该相同。又因为之前生成的虚节点的根节点没有变化，所以虚节点不影响这步验证的正确性。

在这一次遍历中还要为待测树中各节点生成序号。生成的方法是根据名称同标准树中对应节点的序号相匹配。若同一名称可以在标准树中找到多个节点，则进一步比较节点的取值。例如标准树中的节点xi和xj的名称都为a，值分别为0和1，待测树中某一节点的名称为a，值为1，则该节点的序号为j，节点表示为xj’。由之前记录的xi和D（xi），可以得到对应的xi’和D（xi’）。

验证完待测树中各节点的父节点后，还需要进一步验证各节点之间的相关性。按照广度优先遍历的顺序再一次遍历待测树，并记录待测树中的各节点的序号。在遍历过程中完成对整个待测树各节点相关性的验证。具体方法如下:

（1）删除待测树的根节点，整个待测树变成待测森林。待测森林中各个新生成的待测树的根节点均变成基本节点（仍然不能区分是必备节点或者可选节点）。

（2）按照从左到右的顺序，验证各个新生成的待测树的根节点。设集合X’＝｛x1’，x2’，…，xm’｝是D（xi’）的解的集合，则节点xj’∈X’存在，是节点xi’存在充分条件。当m＜i时，若集合X’中各元素表示的节点都已遍历到，则xi’通过验证。当m＞i时，若xj’∈X’的序号j＜i，只需判断节点xj’在xi’之前是否遍历到即可；若j＞i，则将节点xj’视为基本必备节点，同时认为xi’通过验证。若xi－1’＝P（xk’），且i－1＞k，xi－1’不存在，则当遍历到xi’时，就可以认为待测树不符合标准结构，xk’和以其为根节点的子树不应该在待测树中存在。

（3）当新生成的各树的各节点遍历完毕后，删除各个根节点，生成新的森林和新的待测树。

（4）重复b到c，直到原待测树中各节点均完成遍历。关于这个算法有以下几点说明。

1）由于之前已经对待测树进行了处理，通过生成虚节点，保证在处理后的待测树中各节点只能有单一取值，因此D（x）中不存在或的关系，全部节点为且的关系。即只有集合X’中各元素对应的节点都存在的情况下，xi才能存在。

2）根据y＝D（x）以及x＝P（y）可知，若节点y存在是x存在的充分条件，则若节点x存在，必能推出节点y一定存在。

3）在这个算法中，不对标准树和待测树的节点分配序号也能完成验证。在第二次遍历的时候，需要比较待测树和标准树中各节点的名称和值。根据上文的叙述，验证节点x时需要查找所有的D（x）是否存在。设所有完成遍历的节点集合为N，那么在这种情况下，每次查找都要从头开始遍历集合N中元素。而采用分配序号的方法，N中各元素按序号顺序排列，在N中查找特定元素的算法就可以根据具体需求选取。

上面的算法可以表示成伪码的形式:

4 时间开销

整个算法需要对待测树和标准树分别进行两次完全遍历。因此，该方法执行时耗费的时间必然和标准树的节点数n以及待测树的节点数n’有关。另外，在判断待测树中某一节点x的存在是否合法的时候，需要查找D（x）中各节点是否被包含在已完成遍历的节点集合中。由于对所有节点分配了序号，因此这一步相当于在一组已排序的数字集合中查找特点数字。其时间开销取决于具体的查找算法。如果t（n）表示完全遍历标准树的时间开销，t（n’）表示完全遍历待测树的时间开销，t（i）表示查找数字i的时间开销，则总的时间开销T＝2t（n）＋2t（n’）＋∑t（i）。

5 实例研究

图3所示是一个已经完成序号分配的待测树T，其中各节点存在的充分条件见表1。

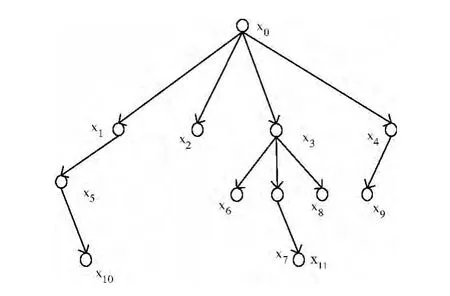
图3 待测树T

待测树T的验证过程如下:

（1）验证x0，通过。

（2）依次验证x1，x2，x3，这3个节点存在的充分条件都是x0，故x1，x2，x3均通过验证。

（3）验证x4，D（x4）＝｛x0，x8｝，x0已通过验证；8＞4，所以认为x4通过验证，将x8插入待验证的节点集合。

（4）验证x5，由于x1已存在，故通过验证。

（5）x6，x7的充分条件是x3，已存在，故通过验证。

（6）D（x8）＝｛x3，x7｝，x3，x7均已存在，所以x8通过验证。

（7）x9存在的充分条件x4已存在，故x9通过验证。

（8）x10存在的充分条件x5已存在，故x10通过验证。

（9）D（x11）＝｛x1，x7，x10｝，节点x1，x7，x10都已存在，所以x11通过验证。

表1 T中各节点存在的充分条件

待测树中节点xi存在的充分条件是D（xi）也存在。所有节点均满足这个条件的话，我们就认为待测树在节点相关性方面符合需求。

6 结束语

当某一项目的所有数据项的组织结构符合树形结构时，各个数据项或元素可以看作是树的节点。若各个数据项之间具有相关性，如何验证各个数据项的取值以及整体的组织结构，这是实际应用中经常遇到的一个问题。为了解决这个问题，本文提出了一个算法。通过验证造成某一个节点取得某一特定值的充分条件是否成立，来验证整个结构。

本文提出的算法可以完成验证工作，但是整个算法需要考虑待测树和标准树两个树形结构。若待测树符合需求，则整个验证过程中，对每个树形结构都要完成两次完全遍历。此外还要进行多次的查找运算，时间开销较大。因此下一步的工作就是探索采用恰当的方法，比如减少树的完全遍历的次数，以减少整个算法的时间开销。

［1］PAN Yan.Introduction to the design and analysis of algorithms［M］.2nd ed.Beijing:Tsinghua University Press，2007（in Chinese）.［潘彦.算法设计与分析基础［M］.2版.北京:清华大学出版社，2007.］

［2］PAN Jingui，GU Tiecheng，LI Chengfa，et al.Introduction to algorithms［M］.2nd ed.Beijing:China Machine Press，2006（in Chinese）.［潘金贵，顾铁成，李成法，等.算法导论［M］.2版.北京:机械工业出版社，2006.］

［3］CHEN Yiming，LI Zhoujun，FU Zigang.Constrained association rule mining algorithm based on FP－Tree［J］.Computer Engineering and Design，2007，28（9）:4450－4454（in Chinese）.［陈义明，李舟军，傅自刚.基于FP－Tree的约束关联规则挖掘算法［J］.计算机工程与设计，2007，28（9）:4450－4454.］

［4］ZHOU Qinliang，LI Yuchen，GONG Aiguo.New algorithms for effectively creating conditional pattern bases of FP－Tree［J］.Computer Application，2006，26（6）:1418－1421（in Chinese）.［周钦亮，李玉忱，公爱国.一种新的高效生成FPTree条件模式基的算法［J］.计算机应用，2006，26（6）:1418－1421.］

［5］DENG Die，LIU Youcheng.Compliance test of software［J］.Journal of Beijing University of Aeronautics and Astronautics，1997，23（1）:68－73（in Chinese）.［邓昳，刘又诚.软件标准符合性测试［J］.北京航空航天大学学报，1997，23（1）:68－73.］

［6］YAN Weimin，WU Weimin.Introduction to data structures（C）［M］.Beijing:Tsinghua University Press，2007（in Chinese）.［严蔚敏，吴伟民.数据结构（C语言版）［M］.北京:清华大学出版社，2007.］

［7］GUO Jinhua，ZHAN Ming.On the binary tree traversal［J］.Science and Technology Information，2010（17）:65（in Chinese）.［郭金华，占明.浅议二叉树的遍历［J］.科技信息，2010（17）:65.］

［8］WANG Fangxiu，ZHOU Kang.Non－recursive algorithm about two binary tree traversal based on a single linked list［J］.Journal of Wuhan Polytechnic University，2012，31（4）:59－63（in Chinese）.［王防修，周康.基于单链表的二叉树非递归遍历算法［J］.武汉工业学院学报，2012，31（4）:59－63.］

［9］YU Yanan，ZHOU Xi.Optimization strategy in generation of path condition［J］.Computer Engineering and Design，2012，33（10）:3995－4003（in Chinese）.［于亚楠，周喜.路径条件生成中的优化策略［J］.计算机工程与设计，2012，33（10）:3995－4003.］

［10］ZHOU Yan，HOU Zhengfeng，HE Ling.Fast multi－pattern string matching algorithm based on sequential binary tree［J］.Computer Engineering，2010，36（17）:42－44（in Chinese）.［周燕，候整风，何玲.基于有序二叉树的快速多模式字符串匹配算法［J］.计算机工程，2010，36（17）:42－44.］

［11］YU Xiushan，YU Hongming.Software testing new technologies and practices［M］.Beijing:Publishing House of Electronics Industry，2006:100－121（in Chinese）.［于秀山，于洪敏，软件测试新技术与实践［M］.北京:电子工业出版社，2006:100－121.］