高效不确定XML复杂Twig查询处理算法

张晓琳，韩雨童，苏龙超，刘立新

（内蒙古科技大学信息工程学院，内蒙古包头014010）

0 引 言

真实世界中的大部分数据都是不确定的，不确定XML数据在工业，通信，金融和军事等诸多领域得到广泛应用。现在已出现很多关于不确定XML数据的Twig查询处理算法，这些算法的本质是基于文档结构，内容选择和概率阈值的查询，而在实际应用中XML查询是比较复杂的，Twig查询语句中通常包含AND，OR和NOT等逻辑谓词，称为复杂Twig查询。目前针对不确定XML复杂Twig查询的研究还很少。

在深入研究XML复杂Twig查询算法的基础上，提出了一种适合不确定XML特性的复杂Twig查询处理算法，算法提出一种路径叶子节点索引结构，将具有相同路径标签的节点聚集在一起，提高路径匹配效率；实现基于不确定XML包含复杂谓词的小枝匹配，快速得到满足条件的查询结果。

1 相关研究

目前针对不确定XML的查询处理，研究者们基于简单小枝模式匹配已经提出了一些快速有效的方法。2009年，Yawen Li等人提出了Holistically Twig算法［1］，该算法采用区间编码，匹配的过程中处理分布类型的节点。2011年，Siqi Liu等人提出了一种基于概率阈值的PXML查询算法［2］，该算法是在查询的同时给出一个概率阈值，将与查询模式匹配并且概率值大于该阈值的结果返回给用户，该算法是基于TJFast算法提出的，是一类基于归并的算法，无法避免小枝归并时大量结构连接操作。

对于普通XML复杂Twig查询处理的研究还处于起步阶段。文献［3］提出一种整体匹配算法可以同时处理OR，AND和NOT谓词的BTwig－Merge算法。查询前先对查询模式进行B－twig规范化，算法利用栈结构过滤掉部分不参与最终结果的节点。对于查询模式中的PC关系，该算法有明显的优势。文献［4］在GTwig Merge的基础上提出了一种能够处理All－Twig模式查询的算法All Twig Merge，并定义了一种将All－Twig模式规范化的方法。但是在查询中存在重复查询节点的情况。文献［5］扩展Twig List算法，针对同时包含OR，AND和NOT谓词的All－Twig模式查询，提出一种整体匹配算法All Twig List，查询时将All－Twig模式作为一个整体，扫描相关的XML节点，留下符合查询模式的节点，最后采用自顶向下的方法对这些节点进行结果匹配。但算法采用栈存储中间结果，进栈出栈在一定程度上造成时间空间的浪费。文献［6］提出了一种路径分区编码，能够有序聚集存储具有相同路径的节点，并且提出XPattern的概念，对查询模式进行简化，还提出整体匹配算法MPTwig，利用路径分区编码的性质，找到满足查询模式的输出节点集。但该算法在查询过程中通过递归，反复遍历查询模式，并存储大量中间结果，造成时间空间上的浪费。Jian liu等人在文献［7］中提出了一种针对不确定XML复杂谓词整体匹配的查询处理算法LTwig。算法以数据流的形式处理文档树中对应查询模式中标签的所有元素，但LTwig查询过程中需要多次扫描查询模式并存在大量的入栈出栈操作。

从上述相关研究分析可以看出，目前处理普通XML复杂Twig查询算法存在诸多问题，有些算法在处理不确定XML查询时会受到一定条件的制约。如重复处理查询节点；查询过程中产生大量中间结果；反复遍历查询模式等。并且目前还没有关于不确定XML数据复杂Twig查询处理的算法。

2 算法理论基础

2.1 不确定XML数据模型

不确定XML文档可以看作一棵包含概率关系的文档树。本文采用P－文档模型Pr XML｛mux，ind｝［8，9］。如图1在不确定XML文档树中，把概率属性节点的分布类型分为2种:一是独立类型节点ind，独立节点在PXML树中出现的概率是相互独立的，不受其它节点的影响。二是互斥类型节点mux，互斥节点在PXML树中只能出现一个节点且不出现其它兄弟节点，或者全都不出现。

2.2 BooleanTwig查询模式

不确定XML文档的Twig模式查询的本质是在不确定XML文档中查找到所有满足Twig模式的XML数据片段，并计算出每个片段存在的概率值。这类查询中还可以同时包含OR，AND，NOT和wildcard等谓词的复杂Twig模式，称之为Boolean Twig查询模式。

Boolean Twig查询模式是由XPath语句转换成一棵查询树，树中的节点由Qnode，Onode，Anode和Nnode组成。如图2为查询语句Q1＝/S［/E OR//A［//C AND//D］］对应的查询模式，其中Onode和Anode节点分别有两个Qnode孩子A，E和C，D。

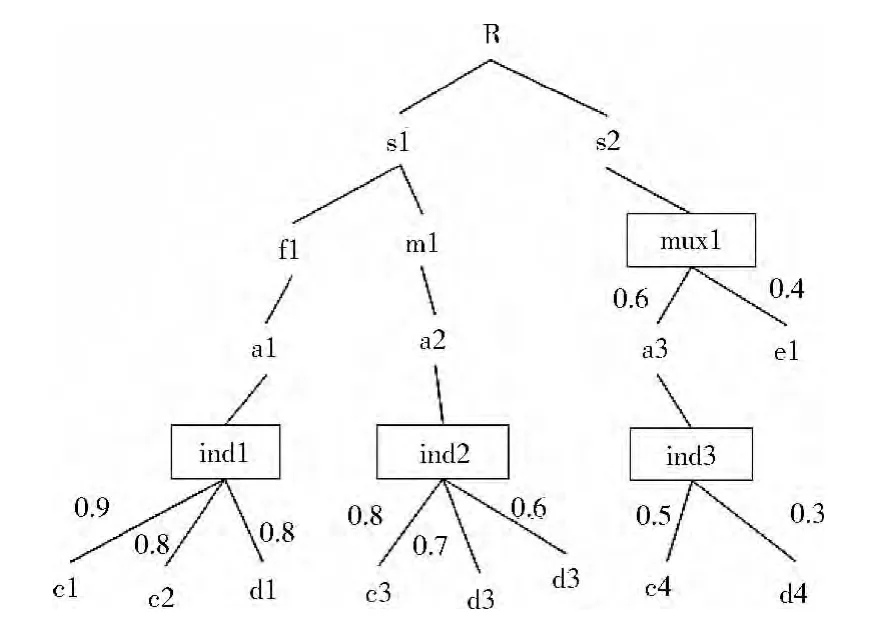
图1 不确定XML文档

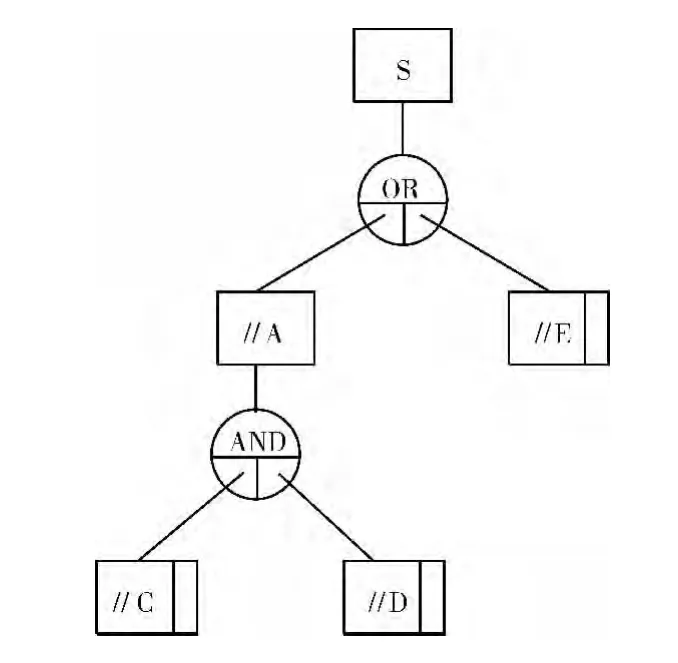
图2 查询模式BT

定义1 存在查询模式BT，对于查询模式中的任意Qnode节点n。若n为根节点，则n.path＝n.name。否则存在路径n.path＝n.name＋n.parent.path，n.path就是查询节点n的查询单枝路径。其中n.paren t是n的所有祖先节点中离n最近的Qnode祖先节点，n.name是谓词“/”或“//”与节点标签的组合。

3 不确定XML复杂Twig查询算法Prob－Boolean－Twig

3.1 REDewey编码

采用（Dewey ID，Prob，Path Prob）元组对不确定XML文档中的每个节点进行REDewey编码。普通节点的De－wey ID用一位表示，即它的EDewey编码值［10］；分布节点的Dewey ID编码用两位表示，其中ind，mux第一位分别用－2，－3表示，第二位是该节点对应的EDewey编码值。如图3为表达方便省略了Pro b和Path Prob（分别记录节点条件概率和存在概率）的两个属性值。因此，根据节点的REDewey编码可以快速判断节点之间的关系。

图3 REDewey编码后的不确定XML文档

关系判断:对任意两个节点u，v，当且仅当L（u）是L（v）的前缀，则u是v的祖先节点。当且仅当L（u）是L（v）的前缀且L（u）比L（v）多且只多一个“.”连接符，则u是v的父亲节点。

为了表示方便和更好的说明Prob－Boolean Twig算法的整体思想，后续部分以图1的不确定XML文档作为例子进行阐述。如无特殊说明，以带下标的小写字母表示节点的标签名称，如s1，a2等，Boolean Twig查询模式中的查询节点用大写字母表示。

3.2 路径叶子索引

在实际应用中，不确定XML文档可能包含数量庞大的节点，表示不确定关系的分布节点使不确定XML文档的结构更复杂，但文档中总是存在大量重复的简单路径。在文档中，简单路径的种类远远小于节点的数量，而且是有限的。例如，116 M经典数据及XMark包含多达1.78＊106个节点，但是其中的简单路径仅有546个。通过统计文档中的简单路径，根据编码后不确定XML文档树，为不确定XML文档树中的所有可能路径建立索引。不考虑分布节点ind和mux，设计路径叶子节点标签索引，即根据所有可能路径叶子节点标签建立索引项，对应节点标签聚集存储简单路径信息及其节点编码，将具有相同路径的节点聚集在一起，加快了路径匹配的速度，有效地提高查询效率。

如图4用大写字母表示路径叶子节点的标签，即索引项，以带下标的小写字母表示文档中节点编码值。例如C是路径叶子节点的标签，将C作为索引项，索引中记录所有以标签C为叶子节点并且去除分布节点的简单路径R/S/F/A/C，及文档树中对应节点的编码值c1＝0.0.0.0.－20.0。

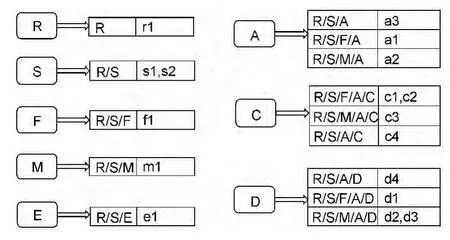
图4 不确定XML文档的路径叶子索引结构

3.3 FA路径匹配

定义2 路径匹配有限状态自动机（finite automation of twig pattern，FATP）是一个五元组:M＝（Q，∑，δ，q0，F）。其中，

Q—状态的非空有穷集合。和q∈Q，q称为M的一个状态。状态个数为查询单枝路径中节点的个数加1。

∑—文档中节点标签集合。

δ—状态转移函数，δ:Q×∑→Q，δ（q，a）＝p。

q0—M的开始状态，也可称为起始状态或启动状态，q0∈Q。

F—M的终止状态集合。F被Q包含。q∈F，q称为M的终止状态。

图5（a）表示查询节点C对应的查询单枝路径为S//A//C，起始状态为q0，终止状态为q3，∑＝｛R，S，A，C，D，E，M｝，图5（b）表示查询节点D对应的查询单枝路径为S//A//D，起始状态为q0，终止状态为q3，∑＝｛R，S，A，C，D，E，M｝。

图5 路径匹配有限状态自动机

3.4 Prob－BooleanTwig算法描述

该算法的主要思想:首先根据不确定XML文档建立路径索引结构，其次采用非归并的整体小枝匹配算法，将叶子节点的查询单枝路径与索引中的路径进行FA路径匹配，得到查询模式中叶子节点对应的解析模式集。根据扩展后编码的性质，递归调用Prob－Boolean Twig算法，不同的逻辑谓词采取不同的处理方式，最终返回满足查询模式的小枝及其存在概率值。

Prob－Boolean Twig算法主函数为boolean Twig－Solution（），递归实现处理不确定XML复杂Twig查询。

算法:boolean TwigSolution（iroot，node）

输入:索引文档根节点和Boolean Twig查询模式的根节点

输出:满足查询模式的小枝和其存在概率值

1.if（node.get Leaf Flag（）＝＝1）//叶子节点

2.｛

3.leaf Result＝leafSolution（iroot，node）；

4. //叶子节点查询处理算法

5. return leafResult；

6.｝

7.else

8.｛if（node.getElement Name（）＝＝"AND"）

9. //实现AND逻辑

10.｛

11. get Together Node（）；//获得孩子节点返回的结果，并合并具有共同祖先的节点

12. cartesian（）；//计算节点之间笛卡尔积，并向上层传递中间结果

13.｝

14.else if（node.getElement Name（）＝＝"OR"）

15.//实现OR逻辑

16.｛

17. get Together Node（）；//获得孩子节点返回的结果，并合并具有共同祖先的节点

18. combiantion（）；//计算节点之间排列组合，并向上层传递中间结果

19.｝

20.else //非叶子节点的Qnode节点

21.｛ children List＝node.getChild（）；

22.for（all child in children List）

23. ｛

24. get Together Node（）；//获得孩子节点返回的结果，并合并具有共同祖的节点

25. return leaf Result；

26. ｝

27. ｝

28.｝

其中，leaf Solution（i root，node）函数根据叶子节点标签在索引中匹配相应的Tab值，经过路径匹配获得满足小枝的所有路径及其对应的文档树中的节点。

3.5 Prob－Boolean Twig算法示例

下面以图2所示的查询模式为例来说明Prob－Boolean Twig算法的执行过程。

首先递归调用boolean Twig Solution（），查询模式中C的查询路径为S//A//C，进行路径匹配后得到如图6所示的解析模式集。因此，最后返回叶子节点C的解析模式集为｛（c1，c2），ind1，a1｝，｛（c3），ind2，a2｝，｛（c4），ind3，a3｝，叶子节点D的解析模式集为｛（d1），ind1，a1｝，｛（d2，d3），ind2，a2｝，｛（d4），ind3，a3｝。执行boolean TwigSolution（AND，A）函数，将底层返回的解析模式集，依据共同的祖先节点（查询路径中上层节点标签）进行合并得到｛（（c1，c2）d1），ind1，a1｝，｛（c3（d2，d3）），ind2，a2｝，｛（c4，d4），ind3，a3｝。因为当前的查询节点为Anode节点，执行cartesian（）函数，计算节点之间组合的满足“与”逻辑和路径存在的概率值，实现AND逻辑。因为概率阈值为0.2，则｛（c1，d1），ind1，a1｝－－0.144，｛（c2，d1），ind1，a1｝－－0.144，｛（c3，d3），ind2，a2｝－－0.144结果被舍弃。继续向上层递归，当执行到当前查询节点为Onode节点时，执行combiantion（）函数，计算节点之间满足“或”逻辑的组合结果，实现OR逻辑并进行阈值过滤，返回给上层解析模式集为｛（c3，d2），ind2，a2，m1，s1｝，｛（c4，d4），ind3，a3，mux1，s2｝，｛e1，mux1，s2｝，其中MUX为互斥节点，舍弃结果｛（c4，d4），ind3，（a3，e1），mux1，s2｝。最后返回满足查询模式的查询小枝及小枝存在的概率｛（c3，d2），ind2，a2，m1，s1｝－－0.224，｛（c4，d4），ind3，a3，mux1，s2｝－－0.6，｛e1，mux1，s2｝－－0.4。

3.6 算法复杂度分析

Prob－Boolean Twig算法执行过程概括为2个阶段:

图6 查询模式叶子节点路径匹配结果

（1）叶子节点路径匹配的过程；

（2）自底向上匹配小枝模式，得到满足查询模式的小枝。

时间复杂度为:阶段（1）查询叶子节点标签对应的路径索引，最坏的情况扫描所有标签，时间复杂度为O（n），其中n表示节点标签数；阶段（2）自底向上匹配过程中，合并有共同祖先的节点标签。函数get Together Node（）最坏情况的时间复杂度为List中每个child Nod e匹配路径个数的积∏L（c），其中L（c）为child Node中匹配路径的个数。因此，Prob－Boolean Twig算法在最坏情况下的时间复杂度为O（n＋∏L（c））。

空间复杂度为:在get Together Node（List child Node）阶段，最坏的情况下的空间复杂度是O（d＊∑L（c）），所有child Node都没有共同祖先节点，其中d表示路径长度，最坏的情况为文档树的深度。因此Prob－Boolean Twig算大的空间复杂度为O（d＊∑L（c））。

4 实验结果分析

采用Java语言实现Prob－Boolean Twig算法，并与经典的All Twig List，MPTwig算法进行对比。实验的硬件环境为:CPU Inter（R）Core i3（2.26 GHz），RAM为2G，操作系统为32位的Windows XP，实验工具为MyEclipse 8.5，JDK 6.0。实验测试所用数据集是在XML经典数据集DBLP文档的基础之上，利用一个随机化的算法随机加入一些分布节点，合成具有不确定性节点的XML数据集。一般情况下，文档中节点的个数要远远高于文档中路径的个数。因此，大小不同的DBLP文档中的节点数量和路径数量见表1。

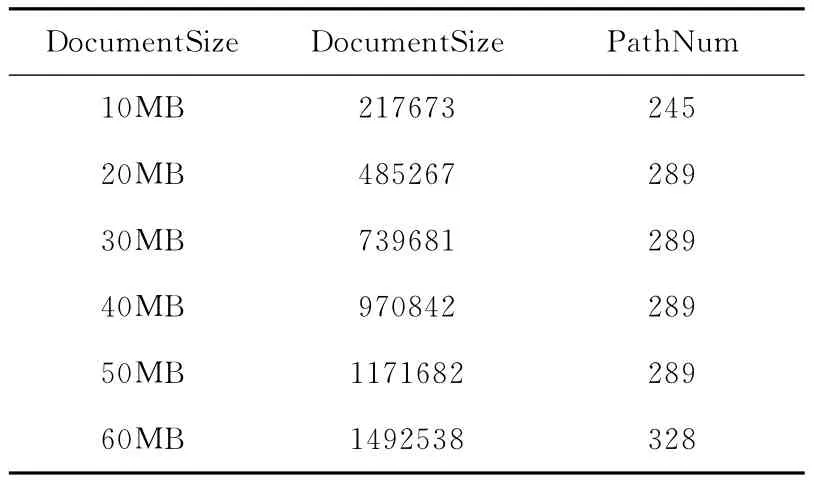
表1 文档相关属性

实验部分共有三组测试来对比两种算法，第一组测试条件是不同概率阈值，相同文档，相同的查询语句；第二组测试条件是相同的文档、不同的查询语句；第三组测试条件是不同的文档、相同的查询语句。每组实验均重复10次，得到的实验数据采用去掉最大值和最小值，取平均值的方法记录整理。实验用到的查询用例见表2。

表2 实验用到的查询用例

第一组实验选取大小为48.7MB的文档，选择Q3作为查询用例，分别选取不同的概率阈值进行测试的响应时间，如图7所示。第二组实验选取大小为82.5MB的文档，查询的概率阈值设定为0.5，分别执行表2所示的4个查询用例，如图8所示。第三组测试选择Q4作为查询用例，查询的概率阈值设定为0.5，选取大小不同的5个文档进行测试，如图9所示。从中可以明显看出，Prob－Boolean Twig算法性能上优于MPTwig和All Twig List算法。因为Prob－Boolean Twig算法在查询过程中仅需要遍历一次查询模式，提高了查询速率；只对查询模式中的叶子节点进行路径匹配并且根据概率阈值过滤掉不满足条件的中间结果，在很大程度上节约存储中间结果所消耗的时间和空间。而MPTwig算法在查询过程中需要反复遍历查询模式，并且在执行查询前匹配查询模式中所有Qnode节点的解析模式集，浪费了大量的存储空间。All Twig List算法则需要遍历查询模式中标签匹配的所有文档节点，匹配过程需要大量的入栈出栈操作。

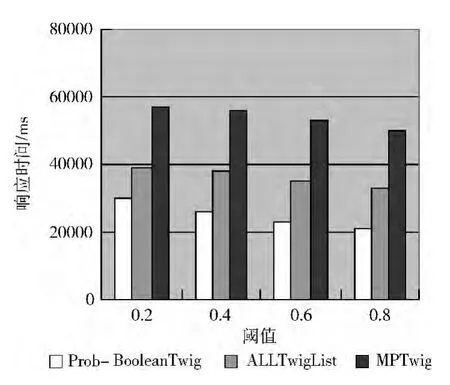
图7 阈值不同时间对比

5 结束语

提出一种针对不确定XML复杂Twig查询匹配处理算法:Prob－Boolean Twig算法。在REDewey编码方案的基础上构建路径叶子节点索引；仅对查询模式中叶子节点进行路径匹配，再采用自底向上的方式对查询模式进行匹配；根据概率阈值对中间结果进行过滤，得到最终匹配小枝及其存在概率值。在理论分析和实验证明方面都表明Prob－Boolean Twig算法在时间和空间上都具有一定的优势。未来工作是对算法进行扩展，来支持wildcard匹配和左右兄弟关系等复杂谓词的Twig查询。

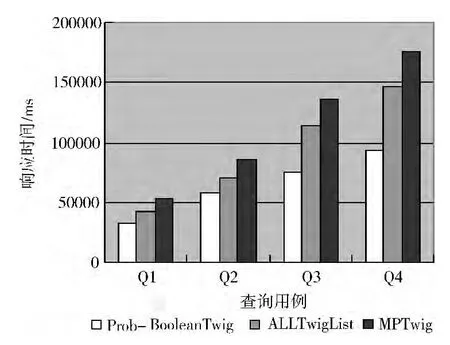
图8 查询用例不同时间对比

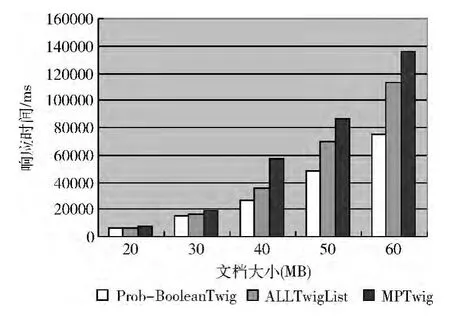
图9 文档大小不同时间对比

［1］Li Yawen，Wang Guoren，Xin Junchang，et al.Holistically twig matching in probabilistic XML［C］//Shanghai，China:Proceedings of the IEEE International Conference on Data Engineering，2009:1649－1656.

［2］Liu Siqi，Wang Guoren.Boosting twig joins in probabilistic XML［C］//Toulouse，France:Proceedings of the 22nd International Conference on Database and Expert Systems Applications，2011:51－58.

［3］Che D，Ling T，Hou W.Holistic boolean－twig pattern matching for efficient XML query processing［J］.Knowledge and Data Engineering，IEEE，2012，24（11）:2008－2024.

［4］Che Dunren.Holistically processing XML twig queries with AND，OR and NOT predicates［C］//Brussels，Belgium:Proceedings of the 2nd International Conference on Scalable Information Systems，2007:1－4.

［5］GUO Hong，WANG Jianhui.Processing algorithm for complex twig with OR，AND，and Not predicates［J］.Journal of Chinese Computer Systems，2010，31（7）:1396－1401（in Chinese）.［郭红，王剑辉.包含OR，AND和NOT谓词的复杂Twig查询处理算法［J］.小型微型计算机系统，2010，31（7）:1396－1401.］

［6］Xu X，Feng Y，Wang F.Efficient processing of XML twig queries with all predicates［C］//Shanghai，China:Proceedings of Computer and Information Science，2009:457－462.

［7］Ma ZM，Liu Jian，Li Yan.Matching twigs in fuzzy XML［J］.Information Sciences，2011，181（1）:184－200.

［8］Abiteboul S，Chan T H，Kharlamov E.Aggregate queries for discrete and continuous probabilistic XML［C］//Lausanne，Switzerland:Proceedings of the 13th International Conference on Database Theory，2010:50－61.

［9］Abiteboul S，Kimelfeld B，Sagiv Y，et al.On the expressiveness of probabilistic XML models［J］.The VLDB Journal，2009，18（5）:1041－1064.

［10］ZHAO Shengmeng，ZHAO Lei.Extended dewey encoding algorithm of twig pattern query without merging［J］.Journal of Chinese Computer Systems，2011，32（5）:837－839（in Chinese）.［赵圣猛，赵雷.一种采用扩展Dewey编码非归并的小枝模式查询算法［J］.小型微型计算机系统，2011，32（5）:837－839.］