原状土基础剪切法抗拔设计的可靠度校准分析

徐 彬，曾二贤，包永忠，冯云巍

(中南电力设计院，湖北 武汉 430071)

原状土基础剪切法抗拔设计的可靠度校准分析

徐 彬，曾二贤，包永忠，冯云巍

(中南电力设计院，湖北 武汉 430071)

结合现行DL/T 5219－2005规定给出的“剪切法”抗拔设计方法及典型地区黏性土和戈壁滩碎石土的试验数据，应用可靠度理论建立输电塔原状土基础抗拔稳定的极限状态方程，确定剪切法计算变量的统计参数和分布规律。基于一次二阶矩法对原状土基础剪切法抗拔设计的可靠度水平进行校准分析，考察了分项系数、抗力变异性及计算模式不定性等参数的影响。结果表明：对黏性土，现行规定的剪切法抗拔设计的原状土基础可靠度指标β约为4.43；对戈壁滩碎石土，计算得到的可靠度水平更高。上述结论可为DL/T5219的修编提供参考。

原状土基础；抗拔；可靠度校准。

1 概述

对于输电塔原状土基础，以往较多的研究注重于其抗拔承载的机理分析及计算预测，到目前为止，对其抗拔可靠度水平方面的研究还鲜见于文献，但最近已受到越来越多的关注。我国DL/T 5219－2005《架空送电线路基础设计技术规定》(以下简称“规定DL/T5219－2005”)针对原状土抗拔设计给出了土重法和剪切法2种方法，但在执行和使用过程中，很多设计单位提出不少疑惑(如2种方法的差异及各自安全度水平，剪切法参数A1和A2的取值困难问题等)，目前针对此也形成了一些有价值的新成果，但较少有对规定DL/T5219－2005中的剪切法可靠度水平展开校准分析。鲁先龙等提出了掏挖基础抗拔极限承载力的计算公式，并对其进行了可靠度分析，但未考虑分项系数、抗力变异性及计算模式的不定性等影响。

本文应用可靠度理论建立输电塔原状土基础抗拔稳定的极限状态方程，结合典型地区黏性土和戈壁滩碎石土的试验成果，确定剪切法计算变量的统计参数和分布规律，并基于一次二阶矩法对原状土基础剪切法抗拔设计的可靠度水平进行校准分析，并考察了分项系数、抗力变异性及计算模式不定性等参数的影响。考虑到目前原状土基础在输电线路中应用愈加广泛，为适应我国电力建设事业发展的需要，开展输电线路基础的可靠度水平较系统性的研究很有必要且具有实践意义。

2 剪切法可靠度分析模型

2.1 规定DL/T5219－2005中的剪切法

DL/T5219－2005指出“剪切法”适用于原状抗拔土体，剪切法计算抗拔稳定的计算公式为：

式中： γf为基础附加分项系数；TE为基础抗拔力设计值；RT为基础单向抗拔承载力设计值；γθ为基底展开角影响系数，当θ>45°时取γθ=1.2；当θ≤45°时取γθ=1.0；γE为水平力影响系数；A1、A2为无因次系数，由抗拔土体内摩擦角φ和基础深埋比λ(λ=ht/D)确定；Qf为基础自重。

2.2 极限状态方程

剪切法计算原状土抗拔稳定的工作状态可以统一用抗力R与作用效应S表示为：

随着R和S的变化，功能函数Z有三种变化：当Z＜0时，表示结构处于失效状态；当Z＞0时，表示结构处于可靠状态；当Z＝0时，表示结构处于极限状态。

影响输电线路基础抗力的主要因素包括材料性能的不定性(如土体抗剪强度指标c、φ等)、结构构件几何参数的不定性(如ht、d等)、计算模式的不定性等。这些因素一般均为随机变量，因此，结构构件的抗力R经常是多元随机变量的函数，确定其统计参数及其分布类型是较为困难的，目前国内外一般都是采用间接的方法，即先对影响截面抗力的主要因素分项进行统计分析，确定其统计参数，然后通过截面抗力与各因素间的函数关系，利用统计数学中的误差传递公式推求抗力R的统计参数。

由式(1)和式(2)可知，抗力R主要由三项组成。为便于计算，定义抗力比值ρ1=R1/(R1+R2)，ρ2=R2/(R1+R2)，ρG=RGK/(R1+R2)，则

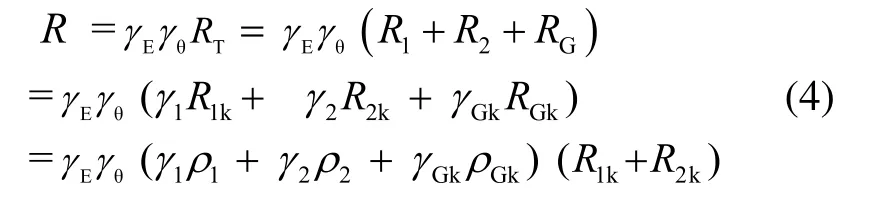
式中： γ1、γ2、γGK分别为0.4、0.8和1。

输电线路基础的荷载主要来自上部结构传递的荷载，为简化计算，本文仅考虑永久荷载+风荷载的组合。以永久荷载产生的效应为基准，定义可变荷载与永久荷载的效应比值为ρ=SQK/SGK，则

考虑计算模式的不定性，可确定剪切法抗拔稳定的功能函数为：

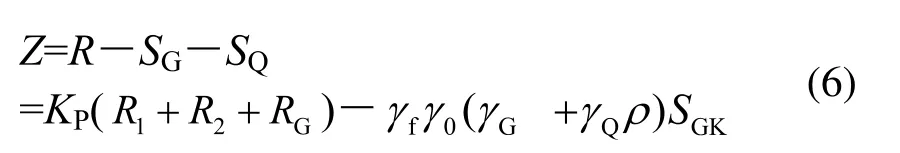
则剪切法抗拔稳定的极限状态方程为：

式中：KP为计算模式不定性系数；γ0为结构重要性系数；γG为永久荷载分项系数；γQ为可变荷载分项系数。

3 基本变量的统计分析

3.1 荷载的统计分析

3.1.1 荷载的统计参数

输电线路基础的荷载类型和统计参数可取为与上部结构一致。对于输电线路铁塔，一般采用一阶弹性方法进行内力分析，所以铁塔结构的荷载效应S与荷载Q之间呈线形关系，即S=CQ，其中C是荷载效应系数。因此，在可靠度分析中，一般认为荷载效应S与荷载Q的统计特征是一致的。

对于永久荷载，其值在设计基准期内基本不变，因此，可以将永久荷载直接转化为与时间无关的随机变量描述。为了简便起见，《建筑结构可靠度设计统一标准》GB50068采用KG=G/Gk这个无量纲参数作为永久荷载的统计变量，其中G为实测重力，Gk为荷载规范规定的标准值。通过对有代表性永久荷载实测数据的统计分析，得到代表永久荷载的随机变量的统计参数为： μKG=1.06，σKG=0.074。用χ2检验或K－S检验，在显著性水平为0.05时，永久荷载的随机变量KG服从正态分布。

对于风荷载，《建筑结构荷载》GB50009在全国随机抽取了一批具有代表性的气象站记录的大风资料，经统计分析认为，在5%的置信度条件下，年最大风压值x可采用极值I型的概率分布。对于铁塔风荷载，国内外已经有大量的研究数据，其随机变量的统计参数为：μKW=0.998， δWOT=0.193。

3.1.2 荷载效应比值

大量的计算结果表明，在最大风荷载参与组合时，风荷载效应与永久荷载效应的比值ρQ在3.3～8.3之间变化。为简化计算，本文在最大风荷载参与组合时，取ρQ＝4.0、5.0、6.0、7.0、8.0。

3.2 抗力的统计分析

3.2.1 基本假定

由前述计算公式可知，影响杆塔基础上拔稳定抗力的因素很多且较为复杂，尤其是系数A1、A2与内摩擦角φ关系更为复杂，非线性程度较高，直接利用统计学中的误差传递公式确定抗力的统计参数难度较大且不准确。为简化计算，作如下假设：

(1)近似认为系数A1、A2与土体内摩擦角φ的变异性相同。

(2)不考虑杆塔基础几何尺寸的变异性。

(3)基础自重变量统计参数与永久荷载统计参数相同。

3.2.2 计算模式的不定性系数KP的统计参数

计算模式不定性系数按下式计算

式中：Rtu为承载力试验值；Rju为理论计算极限值。根据目前收集的输电线路基础原状土抗拔基础极限承载力的试验资料，KP计算列于表1～表3中。

表1 c、φ 、γ 、R1j、R2j、RGj的统计参数

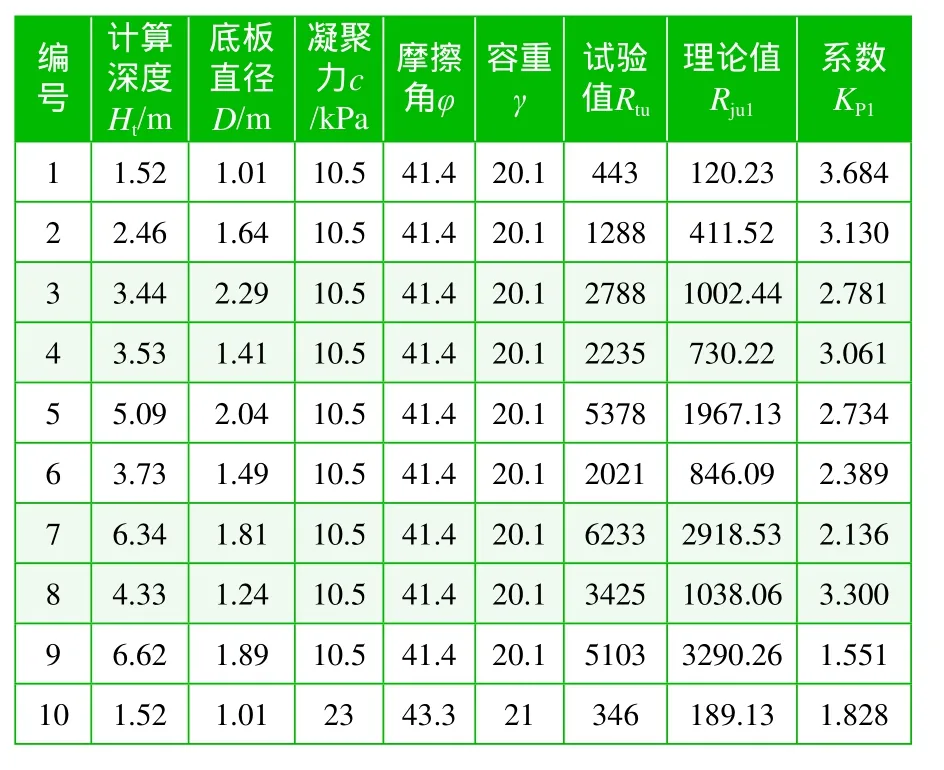
表2 戈壁土地区原状土基础KP(文献[2])

续表2

表3 戈壁土地区原状土基础KP(文献[13])

续表3

根据表1～表3所列数据，以所计算的KP为统计样本，用K－S检验，在5%的置信度条件下，KP可按对数正态分布，见图1和图2。根据参数估计，其统计参数为均值 μKp1=2.67，δKP1=0.306；μKp2=2.67，δKP2=0.306。

图1 戈壁土地区KP1的K－S检验

图2 黏性土地区KP2的K－S检验

3.2.3 R1、R2、RG的统计参数

在不考虑几何尺寸影响的情况下，R1、R2、RG主要与c、φ、γ值有关。直接确定c、φ、γ的均值不具有代表性，一般采用均值系数来进行描述，即μKxi=μxi/Xik，其中μxi为变量Xi的均值，Xik为变量Xi的标准值。

文献[14]～文献[17]进行了大量的统计分析，得出c、φ、γ的统计参数，见表1。其中，c、φ的变异系数δc和δφ为0.146～0.273和0.12～0.179 ，取其平均值为0.232和0.143。

根据前述假定，A1、A2的统计参数与土体内摩擦角φ的统计参数相同，则μKA1=μKA2=1，δA1=δA2=0.143。由于抗力R1、R2、RG是由多个影响相近的随机变量相乘而得，即R＝X1·X2·…·Xn(X1，X2，…，Xn为影响结构抗力的随机变量)，上式两边取对数则有lnR＝lnX1+lnX2+…+lnXn，由中心极限定理可知，当n充分大时，则lnR近似服从正态分布，而R则近似服从对数正态分布。所以在实际应用中，不论Xi(i=1,2,…)服从什么分布，可将R作为一个综合变量，且近似服从对数正态分布，其统计参数则利用统计数学中的误差传递公式求得。根据误差传递公式，可得出R1j、R2j的统计参数计算公式为：

计算结果见表4。

表4 黏性土地区原状土基础KP(文献[2])

续表4

抗力R的统计参数按下式计算：

3.2.4 抗力效应比值

抗力效应比值直接影响抗力的统计参数。经过本文大量计算，ρ1的取值范围为0.2～0.9，平均值为0.6，ρG的取值范围为0～0.6，平均值为0.1。本文在进行可靠度计算时，取ρ1=0.3、0.4、0.5、0.6、0.7、0.8分别进行计算。

4 可靠度校准分析

4.1 可靠度校准分析的方法和步骤

根据基本变量的统计参数，采用一次二阶矩法计算可靠指标，其主要计算步骤如下：

(1)假定作用效应SGK为某一定值，则

(2)根据荷载和抗力的均值系数μKXi和变异系数δXi，计算各随机变量的均值μXi和标准差σXi。

(3)假定各随机变量Xi的设计验算点P*的坐标值为Xi*(R*，S*)，对非正态变量进行当量正态化。

(5)按下式计算方向余弦cosθi。

(6)计算μXi、σX'i和cosθi代入下式计算可靠指标β。

(8)判断|上次β－本次β|≤允许误差。若满足允许误差，则本次求得的β即为所求的可靠指标；否则，将求得的X*i代入式(17)～式(18)，重复步骤(19)～步骤(21)。

4.2 可靠度校准的结果与分析

可靠度指标β的计算结果见图3和图4。

图3 戈壁土地区可靠指标计算结果

图4 黏性土地区可靠指标计算结果

值得一提的是，上述按结构重要性系数取1.0，抗拔土体滑动面形态参数n暂取为4计算。由图3～图4可以看出：

(1)原状土基础剪切法抗拔可靠指标β对荷载效应比值ρ=4～9之间时较为敏感，在ρ=7时处于较低值，对可靠度校准而言，可取平均值来评价现行规定DL/T5219－2005的可靠度水平。

(2)对于黏性土，原状土基础剪切法抗拔可靠指标β的平均值为4.43。结合文献可知，黏性土原状土基础的剪切法抗拔可靠度水平偏高。

(3)对于戈壁滩碎石土可靠度指标β的平均值为6.96，远高于一级结构的最低可靠指标，这主要是因计算模式不定性系数Kp取值较高所致。因此，规定DL/T5219－2005公式是否适用于戈壁滩碎石土及形态参数n的取值，有待进一步研究。

5 结论

通过建立输电塔原状土基础抗拔稳定的极限状态方程，结合典型地区黏性土及戈壁滩碎石土的试验成果，采用一次二阶矩法对现行规定DL/T 5219－2005中剪切法抗拔设计的可靠度进行校准分析。得到的主要结论如下：

(1)提出了一种原状土基础剪切法抗拔可靠度校准分析的步骤和方法，该方法简易可行。

(2)提出了抗力统计参数的近似分析方法，得出了抗力的均值系数和变异系数。

(3)原状土基础剪切法抗拔可靠指标β对荷载效应比值ρ=4～9之间时较为敏感。

(4)对于黏性土，原状土基础剪切法抗拔设计的可靠度指标β平均约为4.43，可靠度水平偏高；对于戈壁滩碎石土，其计算得到的可靠度水平更高，且偏于安全过多。建议可进一步开展规定DL/T5219－2005计算公式的适应性研究工作。

[1]DL/T 5219－2005，架空送电线路基础设计技术规定[S]．

[2]鲁先龙，等．输电线路掏挖基础抗拔极限承载力的可靠度分析[J]．电网与清洁能源，2012，28(1)．

[3]王学明，王虎长，胡建民．送电线路掏挖基础抗拔力理论计算公式修正[J]．电网与清洁能源，2007，23(8)．

[4]覃伟平， 曾二贤， 王开明．基于剪切法分析输电塔原状土基础的抗拔极限承载力[J]．华中电力，2 010， (04)．

[5]鲁先龙，等．戈壁碎石土地基原状土掏挖基础抗拔试验研究．土木建筑与环境工程．2012，34(4)．

[6]李正民．土体抗拔性能的试验研究及其理论分析[C]．高压输电线路学术讨论会论文集，1981．

[7]赵国藩．工程结构可靠性理论与应用[M]．大连：大连理工大学出版社，1996．

[8]GB 50068－2001，建筑结构可靠度设计统一标准[S]．

[9]白国良，刘明副．荷载与结构设计方法[M]．北京：高等教育出版社，2003．

[10]GB 50009－2001，建筑结构荷载规定[S]．

[11]李英民，等．送电线路杆塔结构可靠度影响参数及规律研究[J]．工业建筑，2010，40(7)．

[12]李彦民．送电线路杆塔结构风荷载作用下可靠度分析及应用研究[D]．重庆：重庆大学，2007．

[13]中国电力工程顾问集团中南电力设计院，中国电力科学研究院．《架空送电线路基础设计技术规定》修订专题报告一：原状土基础抗拔计算[R]．北京：中国电力工程顾问集团中南电力设计院，中国电力科学研究院，2012．

[14]侯建国，安旭文．《碾压式土石坝设计规定》修订专题研究报告：WHU－04土石坝坝坡抗滑稳定可靠度校准分析[R]．武汉：武汉大学土木建筑工程学院，2006．

[15]范明桥．土压力计算与参数的概率特性研究[J]．水利水电勘测设计标准化，1997，(3) ．

[16]范明桥．黏性填筑土强度指标c、φ的概率特性[J]．水利水运科学研究．2000，(1)．

[17]陈立宏，陈祖煜，刘金梅．土体抗剪强度指标的概率分布类型研究[J]．岩土力学，2005，26(1)．

[18]余安东，叶润修．建筑结构的安全性与可靠性[M]．上海：上海科学技术出版社，1986．

[19]GB 50153－2008，工程结构可靠性设计统一标准[S]．

Credibility Adjusting Analysis of Cut Method Resistance Drawing Design of Original State Earth Foundation

XU Bin, ZENG Er-xian, BAO Yong-zhong, FENG Yun-wei
(Central Southern China Electric Power Design Institute, Wuhan 430071, China)

Based on the uplift design of shearing method by current DL/T 5219－2005 regulations and the test data of the typical area with clay plus the gobi desert soil, the uplift limit state equation of transmission line undisturbed soil foundation were proposed, and the statistical parameters plus distribution of shearing method calculation variable were determined. Using “the first order second order method”, uplift design reliability level of undisturbed soil base were calibrated calculated, and the parameters sensitivity of partial factor, resistance variability plus calculation mode uncertainty were analysed. The results show that: For clayey soil, the undisturbed soil foundation uplift reliability index of shearing method by current regulation is about 3.89; For gobi desert soil, the calculated reliability index is higher. The above conclusions can be as references for DL/T5219 revision.

undisturbed soil foundation; uplift; reliability calibration.

TU312

A

1671-9913(2014)03-0058-07

10.13500/j.cnki.11-4908/tk.2014.03.012

2013-05-28

徐彬(1987- )，男，湖北洪湖人，硕士，工程师，主要从事输电线路结构和基础设计研究工作。

book=67,ebook=574