基于迭代协作的改进DV-Hop定位算法
新华社音视频部 邰剑秋
介绍
在无线传感器网络中,节点准确地进行自身定位对其有效性起着关键的作用。为了适应无线传感器网络中节点低能耗的特性要求,充分利用节点资源,在节点定位中引入协作技术,以获得更高定位的性能,即协作定位[1]。
对于无线传感器网络节点定位算法主要可以分为两大类:基于测距的定位算法和无需测距的定位算法。测距技术主要包括基于TOA的定位、基于TDOA的定位、基于AOA的定位、基于RSSI的定位等[1][2]。无需测距的算法主要包括以下几种:质心算法[3]、APIT算法[4]、MDS-MAP算法[5]、DV-Hop算法[6]等。上述算法中,DV-Hop算法具有方法简单、定位精度较高等优点,但其定位性能受节点分布影响大,仅在密集网络中,才能达到较高定位精度,当网络拓扑不规则时,定位误差较大。
文献[7]通过加入接收信号强度指示器(RSSI)测距模块辅助定位,对算法进行改进,提高了定位精度和系统稳定性。但是需要增加额外的测距模块,使硬件复杂度增大,有悖于无需测距算法简单易行、成本低的特点。文献[8]提出了一种选择边界锚节点的算法,通过减少参与洪泛的锚节点个数来减少能量消耗,但是该方法对定位精度改善甚小,且网络拓扑稀疏、信标节点较少或分布不规则时,对算法性能影响较大。文献[9]从获得跳数的方法上对DV-Hop算法进行改进,利用节点接收到的信号能量对节点间跳数进行量化。文献[10]利用节点与其邻近节点间的测量距离优化定位性能,但其定位精度主要依赖于求精阶段节点间距离测量的精度,当距离误差较大时,定位误差反而增大。同时,[9][10]还分别需要得到能量和待测节点间距离等额外信息,使通信开销和硬件复杂度增大。文献[11]从求平均每跳距离、校正值的选取上对算法作改进,且引入未知节点到参考节点的距离作为节点定位的约束条件,提高了定位性能且节约了成本。但是,由于DV-Hop算法使用跳段距离代替实际距离来估算未知节点的定位坐标,跳数越大则误差越大。且定位精度还受节点拓扑关系影响,当信标节点位置近似于一直线时,定位误差较大。同时,传统的DV-Hop定位算法覆盖范围还受到信标节点个数的限制,即当信标节点较少时,将有很大一部分未知节点无法实现定位。
本文针对以上问题,提出了一种优化的DV-Hop定位算法,即ICDV-Hop算法。通过设置跳数门限来控制节点间的距离误差,并且利用共线度测试对信标节点之间、信标节点与未知节点间的几何位置关系加以约束,以选择最优的信标三角形来降低定位误差,并引进了迭代协作[12]增加定位覆盖。该算法使用3个信标对未知节点进行位置估计,有效降低了定位时的计算能耗。仿真结果表明,ICDV-Hop算法的平均误差和定位覆盖均有明显改善,表现出良好的可靠性,并且有更好的稳定性和鲁棒性。
系统模型
DV-Hop算法整个定位过程不依赖于昂贵的测距方法,利用了多跳信标节点信息来参与节点定位,使其定位覆盖率大大提高。其主要思想是采用跳段距离之和代替实际距离。整个网络结构如图1,实线为跳段,说明相应节点间可以实现通信。
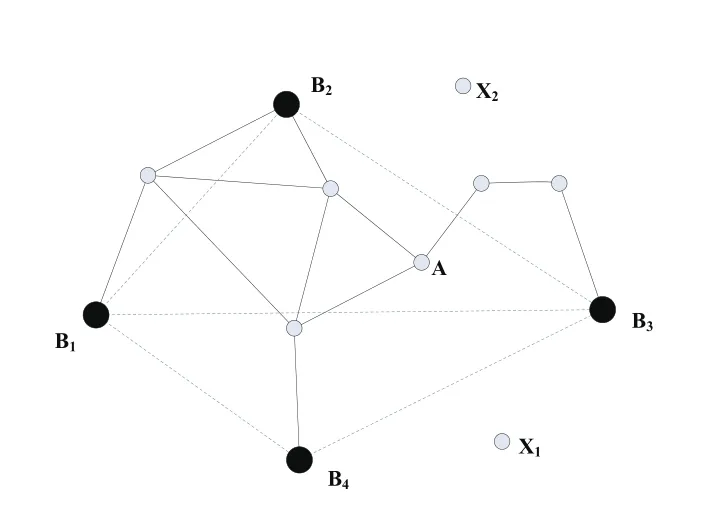
图1 网络拓扑结构
图中B1, B2, B3, B4为信标节点(Beacon),其余为未知节点。X1, X2代表剩余节点,即无法实现位置估计的节点。
传统DV-Hop算法由三个阶段组成。第1阶段,使用典型的距离矢量交换协议,通过节点间的信息交换,使网络中所有节点获得与信标节点间的跳数。如图1中,节点A获得与信标节点B1、B2、B3、B4间的跳数分别为3、2、3、2.第2阶段,在获得其他信标节点的位置信息和条数信息后,信标节点计算节点间的平均每跳距离,并将其作为一个校正值(correction)广播至网络中。未知节点利用校正值和记录的跳数计算与各信标节点的距离。第3阶段,根据未知节点与每个信标节点的距离和信标节点的位置坐标,利用多边测量或极大似然估计法计算未知节点坐标。
ICDV-hop算法
由于DV-Hop算法节点间的距离由平均每跳距离与跳数相乘求得,如图1所示,定位精度主要由平均每跳距离的精度决定,而跳数越大估计得到的平均每跳距离越不准确,导致节点间距离误差过大,最终影响定位精度;定位精度受到节点间位置关系影响,当用于定位的信标节点处于同一直线时,定位误差较大;定位覆盖范围受到信标节点个数的限制,而实际网络中信标节点往往较少,导致较多未知节点无法实现定位。因此本文针对以上三点对DV-hop算法作出改进,ICDV-Hop算法主要由5个步骤组成:
1. 通过节点间信息交换,获得未知节点与跳数门限内信标节点的跳数信息;
2. 根据信标节点校正值与跳数信息计算未知节点到信标节点的距离;
3. 进行信标节点共线度测试,选择最优的信标三角形;
4. 未知节点利用信标三角形进行位置估计;
5. 判断每个已定位节点的定位误差,若其小于设定的阈值,则转化成信标节点;
6. 重复第1-4步对剩余的未知节点进行定位,直至没有新的信标节点产生。
3.1 未知节点获得跳数信息
通过节点间的信息交换,能使网络中所有节点获得与信标节点之间的跳数。但由于DV-Hop算法采用跳段距离之和代替实际距离,跳段数增加将使累计误差增大,所以一般情况下,未知节点若只接收距离较近的局部范围内的信标节点信息,将会减少这种累计误差的叠加,提高定位精度并从整体上降低网络通信量。因此,我们设置一个跳数门限N,限制未知节点接收大于此门限跳数的信标节点信息。
如图1所示,信标节点Bi向邻居节点广播自身位置信息,包括跳数字段(Hops)、坐标值和ID号。当未知节点与信标存在不同路径时,选取最小的跳数值计算。未知节点收到某一信标节点的跳数值后,将其与门限N比较,若小于门限N,节点将跳数值加1,并转发给邻居节点,否则丢弃此分组。
门限N与节点传播半径、网络区域面积和信标节点个数有关。可以根据(1)式计算N值

其中,area为正方形网络的边长,R为节点传播半径,BeaconAmount为信标节点的个数,m为每个未知节点定位需要的信标数。
3.2 计算跳距
利用跳数和平均每跳距离,计算未知节点与限定跳数内的信标节点的距离。
首先计算每个信标节点的校正值。设信标节点共有k个,位置信息坐标为(xi, yi) (i=1,2,…,k),每个信标节点根据记录的与其它信标节点的位置信息和相距跳数,估算如图1所示的平均每跳距离HopSize,即每个信标的校正值。信标间的距离为

其中h i , j是对应信标节点间的跳数值。
信标节点得到自身校正值后,将其作为一个跳距校正值(correction)广播至网络中。未知节点仅记录收到的第一个校正值作为平均每跳距离或跳段数最小的作为平均每跳距离。使用这种方法可以使未知节点从最近的信标接收校正值。未知节点获得该校正值后,根据(4)式计算第n个未知节点到各信标节点的距离:

其中cn为未知节点n接收到的校正值,hn , j为未知节点n与信标节点j间的跳数。
3.3 信标三角形的选择
传统算法中,与未知节点通信的信标达到三个时,即可实现位置估计。然而当信标节点接近于同一直线时,会导致较大的位置估计误差。因此将信标节点的位置关系引入到ICDV-Hop算法中,提出共线度概念,如图2所示。

图2 共线度
其中,设平面上任意三点所形成的三角形中最长边的边长为lmax,该边所对应的高即为hmin,定义hmin与lmax的比值为该三角形的共线度,用DC表示为:
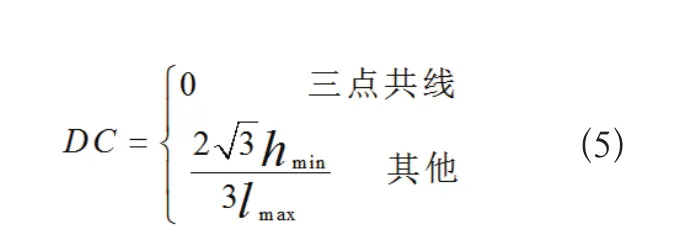
共线度的取值范围为[0,1],共线度值越小表示3个点越接近共线,而当三点完全共线时,三角形退化,此时的共线度为0。在实际的信标节点选择过程中,可以通过设定某一阈值来约束信标节点之间的拓扑关系,即DC< thre_c。其中thre_c为设置的共线度阈值。
尽管通过信标节点的坐标可以方便地计算出它们之间的拓扑关系,但是仅仅考虑信标节点之间的关系是不够的,在未知节点的位置估算过程中,还需要考虑信标节点与未知节点之间的关系。图1中,对于未知节点A,若信标三角形B1B2B3与B1B3B4共线度相等且最优,但A处于三角形B1B2B3中,因此应选择其作为信标。
为了约束未知节点与信标节点之间的关系,需要在设置共线度阈值时考虑未知节点与信标节点之间的位置关系。ICDV-Hop算法通过判断未知节点是否在信标三角形内,选择合适的信标三角形。即先根据共线度测试找出所有可用的信标三角形组合;接着根据步骤2中得到的未知节点到信标三角形各顶点的距离和信标三角形各边长,可以判断出该未知节点是否在相应的信标三角形内,找出符合条件的信标三角形;若此时符合条件的组合有多个,则选取未知节点到信标三角形三个顶点跳数和最小的组合,此做法也与步骤1中增加跳数门限相对应,目的也在于尽可能的减小距离误差。按照这种规则,图1中将选择使用信标B1B2B3来估计A点位置。
3.4 位置估计
当信标节点通过共线度验证后,进行位置估计。
设未知节点A坐标为(x, y),可与其通信的所有k个信标节点的位置信息用(x1, y1), (x2, y2),…,(xk, yk)表示,未知节点到信标节点的距离分别为r1,r2,…,rk,则可建立线性方程组:

其中,

在传统DV-Hop算法中,未知节点在实现自身定位时使用了所有可以与它通信的信标。而由于未知节点与信标节点的距离通过跳数估计得出,多个距离方程构成的超定方程组,当方程个数增加时,它的解并不一定最接近真实坐标值。相反,当跳数过大时,用多个信标定位反而有可能造成误差的扩大,且计算复杂度增加。而ICDV-Hop算法利用跳数门限结合共线度测试,挑选出最优的三个信标节点组合,有效避免了上述情况,且定位误差受网络拓扑影响小。同时,改进算法只使用三个信标节点进行位置估计,与传统算法相比,可以大大节省定位时的计算能耗。
3.5 迭代协作
信标节点的个数直接影响算法定位覆盖范围,而实际网络中信标节点往往较少,致使很大一部分未知节点无法实现定位。针对此问题,本文在ICDVHop算法中引入迭代协作技术。即对于收到足够多信息的节点,用现有算法直接定位;然后已定位节点转化为信标节点,并将自己的位置信息广播出去,剩余节点可以利用该信息定位。
该方法能有效提高定位覆盖,使原本不在信标节点传播范围内的未知节点也能被定位。但是若定位出的未知节点位置与实际位置误差较大,则在将它转化成信标节点供其他节点使用并进行多次迭代时会造成误差传播,使整个网络的定位性能受影响。因此本文在将定位出的未知节点转化成信标节点时加入一定的限制。即:设定一个阈值err_thred,在某未知节点实现自身定位后,计算其归一化定位误差,若误差小于这一阈值,则可转化为信标节点以供下一轮定位,若误差超过这一阈值,则不转化。
迭代协作过程如下:
1. 定位出所有收集到足够信息的未知节点;
2. 计算出上一步中每一个已定位未知节点的定位误差,与阈值err_thred比较,将定位误差小于该值的节点转化为信标节点,其余不转化;
3. 利用转化的信标节点结合原有信标节点,重复1、2对剩下的未知节点再次进行定位,直至没有新的信标节点可以转化。
算法仿真
本文基于图1的系统模型用Matlab软件对ICDV-Hop算法进行蒙特卡洛仿真。仿真过程中网络区域为100m×l00m的矩形区域,信标节点和未知节点的坐标随机产生,随机分布。在相同条件下,分别通过改变信标节点个数和节点密度、节点传播半径等条件来实现对新算法的性能评估。
本文对算法的评估指标主要有两个:归一化平均定位误差err和定位剩余。其中err由节点平均定位误差与传播半径R的比值得出,即
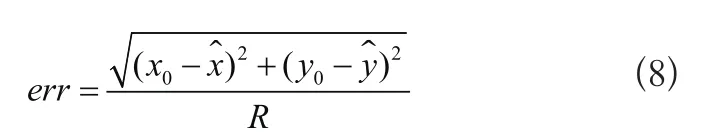
其中(x0, y0)为节点实际位置坐标,($x,$y)为估计坐标。定位剩余是指定位完成后无法定位的未知节点个数占未知节点总个数的比例。值得注意的是最终实验结果通过将多次仿真的数据求平均得到。
图3、图4中区域内总节点数为150,可见在相同信标个数条件下,ICDVHop算法与传统算法相比定位误差降低了约30%,定位剩余也明显减少,表现出优越的定位性能。图3中随着信标节点的增加,定位误差所受影响较小,并逐渐趋于稳定。因为DV-Hop算法使用跳段距离代替节点间的实际距离进行定位估计,信标节点个数增加并不一定能提高定位精度。ICDV-Hop算法只选取3个信标节点用于最后位置估计,当信标节点个数增加到一定程度后,对所选择的信标三角形的优越性影响很小,即定位精度也逐渐趋于稳定。
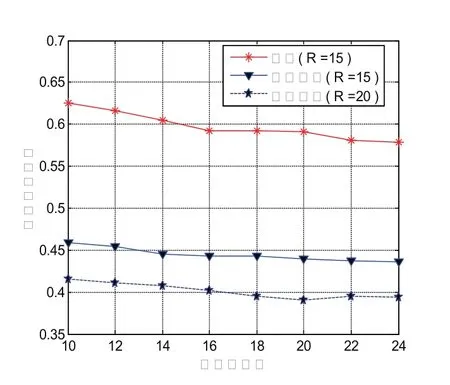
图3 归一化平均定位误差
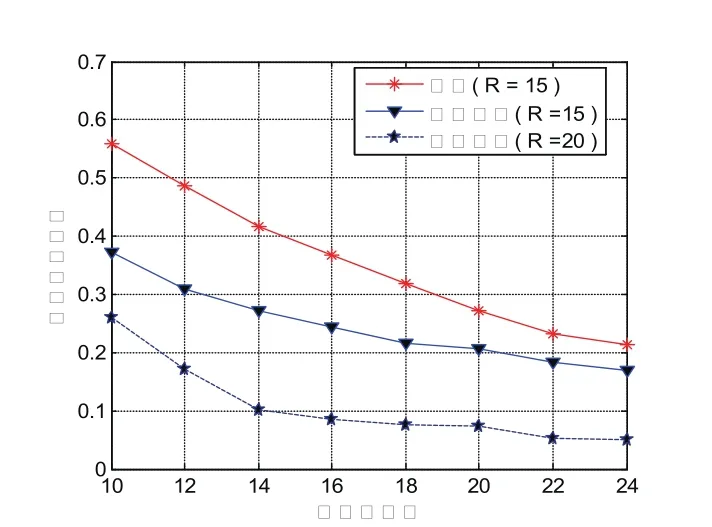
图4 剩余节点比例
图5、图6显示了定位精度与节点密度的关系。图5是保持信标节点个数不变(15个)的情况,改变节点密度相当于只增加未知节点个数;图6是保持信标百分比不变(10%)的情况,改变节点密度相当于信标节点与未知节点均按比例增加。总体上,改进算法比原算法有更小的平均定位误差,尤其是在节点密度较低即网络较稀疏情况下,改进程度尤为明显。在节点密度为0.01而其他条件均相同的情况下,平均定位误差减小了约50%。随着节点密度的增加,传统算法和改进算法定位精度均随之改善,因为节点的增加能提高跳段距离估计精度,从而降低定位误差。且改进算法随着节点密度增加其定位误差相对稳定,表现出良好的鲁棒性,这是由于跳数门限的应用限制了未知节点与信标节点间的条数,从而减小了节点密度对定位性能的影响。
从图7可以看出,随着R的增大,传统算法和改进算法定位误差都随之减小。而在相同条件下,改进算法比传统算法表现出更优越的性能,尤其在R较小时,定位误差改进程度尤为明显。因为在R较小的情况下,使用传统算法定位时,未知节点必须通过较多跳数获得与信标节点的信息,跳段距离误差大导致定位误差过大。而改进算法中由于使用了跳数门限,避免了这种情况。且根据公式(1),条数门限N随着R的增大而减小,限制了节点通信半径对定位精度的影响,因此ICDV-Hop算法具有良好的稳定性。
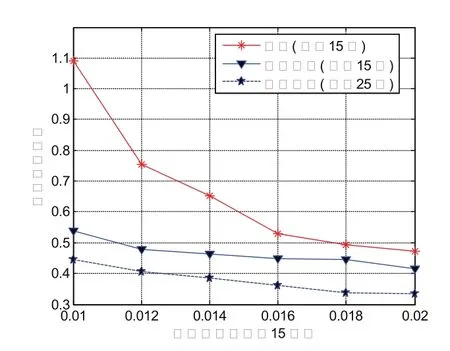
图5 归一化平均定位误差(信标不变)
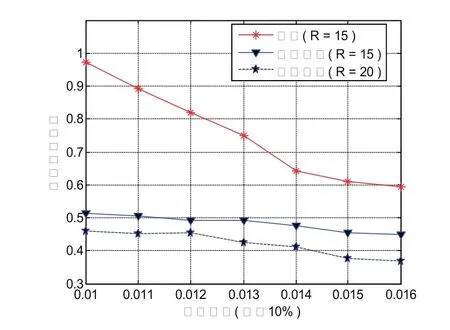
图6 归一化平均定位误差(信标10%)
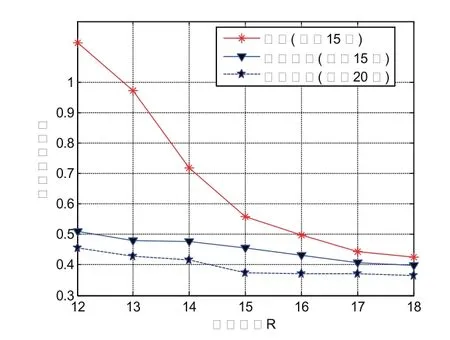
图7 归一化平均定位误差
结论
DV-Hop算法是一种无需测距的分布式节点定位算法,受环境因素的影响小,且节点不用附加额外的测距模块,因而节点简单、费用低、易于实现,适合大规模的无线传感器网络应用。但是由于未知节点到锚节点之间的距离用网络平均每跳距离和两者之间跳数的乘积表示,在密集的规则布局的网络中可以得到合理的平均每跳距离,从而能够达到适当的定位精度,但在稀疏或不规则的网络中精确度不高。
本文针对无线传感器网络特点和传统DV-Hop定位算法的局限性,对其提出了3点改进措施。通过设置跳数门限来控制节点间的平均每跳距离误差;并且利用共线度测试对信标节点、信标节点与未知节点间的几何位置关系加以约束,以选择最优的信标三角形来降低定位误差;引进了迭代协作技术,将定位误差小于设定阈值的已定位节点转化成信标,进行多次迭代定位,从而避免误差传播并增加定位覆盖。从分析与仿真结果可以看出,改进算法在平均定位误差及算法覆盖等方面比传统的DV-Hop方法有较大改善,表现出了更加优越的性能,在网络中信标节点比率较低及网络稀疏的情况下,改进程度尤为明显。且改进算法性能受网络条件影响较小,具有良好的鲁棒性。
[1] Patwari N, Ash J N, Kyperountas S,et al. Locating the Nodes: Cooperative localization in wireless sensor networks.IEEE Signal Proccesing Magazine, 2005,22(4):54-89
[2] Della R F, Ardhy W S, Gianluca S, et al. Experimental Activity on Cooperative Mobile Positioning in Indoor Environments. In: IEEE International Symposium on a World of Wireless Mobile and Multimedia Networks. Espoo, Finland: 2007. 1-6[3] Bulusu N, Heidemann J, Estdn D.GPS-less Low-cost Outdoor Localization for Very Small Devices. IEEE Personal Communications, 7(5): 28-34
[4] Tian H, Chengdu H, Blum B M,et al. Range-free Localization Scheme for Large Scales sensors Networks.In: Proceedings of the 9th Annual International Conference on Mobile Networking. New York, USA: 2003.81-95
[5] Shang Y, Ruml W. Improved MDS-based localization. IEEE Computer and Communications Societies, 2004, 4: 2640-2651
[6] Nicolescu D, Nath B. DV based positioning in ad-hoc Telecom.Systems. Telecom. System, 22(1),2003: 267-280
[7] 刘艳文,王福豹,段渭军等.基于DV—Hop定位算法和RSSI测距技术的定位系统.计算机应用,2007,27(3):516-518
[8] 姜山,李建波.一种改进的DV-Hop传感器网络定位算法.计算机工程与应用,2007,43(34): 141-143
[9] Li X, Shi H, Shang Y. A partialrange-aware localization algorithm for ad-hoc wireless sensor networks.In: Proceedings of the 29th Annual IEEE International Conference on Local Computer Networks (LCN). Tampa,USA: 2004. 77-83
[10] Savarese C, Rabaey J, Langendoen K. Robust positioning algorithm for distributed ad-hoc wireless sensor networks. In: Proceedings of the USENIX Technical Annual Conference.Monterey, California: 2002. 317-327
[11] 嵇玮玮,刘中.DV-Hop 定位算法在随机传感器网络中的应用研究.电子与信息学报,2008,30(4):970-974
[12] Savvides A, Han C C, Srivastava M B. Dynamic fine-grained localization in ad-hoc networks of sensors.In: Proceedings of the 7th Annual International Conference on Mobile Computing and Networking. New York, USA: 2001. 166-179

