技能评分项目裁判员评分结果的多面Rasch模型分析——项目反应理论在体育运动领域的应用

何 壮,赵守盈

(1.北京师范大学教育学部,北京 100875;2.贵州师范大学教育科学学院,贵州 贵阳 550001)

技能评分项目裁判员评分结果的多面Rasch模型分析
——项目反应理论在体育运动领域的应用

何 壮1,赵守盈2

(1.北京师范大学教育学部,北京 100875;2.贵州师范大学教育科学学院,贵州 贵阳 550001)

技能类运动项目以裁判员评分作为评定比赛成绩的主要因素,对裁判员评分分析可以得到许多有价值的信息。研究使用多面Rasch模型对伦敦奥运会男子10米台跳水决赛结果进行分析。分析结果表明：运动员能力排序与奥运会比赛结果有差异;比赛中运动员之间状态起伏规律有差异;裁判员之间评分宽严程度一致,但对个别评分等级把握不准确;规则中的动作难度系数与Rasch分析的动作难度之间有差异。Rasch分析得到的信息对裁判选拔、规则修订、运动员备战具有参考价值。

多面Rasch模型;项目反应理论;跳水;主观评分

1 问题的提出

技能评分项目是由若干名裁判依据评分规则同时并独立地对某一名(组)运动员的竞技能力进行主观评判,以决定运动员成绩的运动竞技项目[1]。跳水、体操、花样滑冰等均属于技能评分项目。这类竞技比赛的最终成绩受到运动员自身技能水平的影响,同时也受到比赛场地、时间等情境因素的影响。此外,评分规则和裁判的主观评分也是影响最终成绩的因素。其中,裁判的公平问题一直是公众关注的焦点。因此,裁判员评分结果的分析对运动员备战、裁判选拔、评分规则的修订意义重大。

传统的评分结果分析基于经典测量理论(Classical Test Theory,CTT),以相关分析、极差分析、方差分析为主。但统计学中认为如果样本量小、个体差异大,估计的误差可能很大[2]。受场地和时间等条件影响,竞技比赛对参赛人数和时间都有严格要求。以伦敦奥运会的跳水决赛为例,每名运动员出场6次,由7名裁判员打分,计算成绩时还要剔除两个最高得分、两个最低得分。这种处理方式使得抽样数量更小,增加了测量误差,有可能造成结果的不公平。

与CTT相比,项目反应理论(Item Response Theory,IRT)具有参数不变性的特点,其参数估计不受抽样影响。CTT分析中运动员能力和项目难度不是定义在同一个量尺上,无法推断运动员在某一项目上会出现怎样的反应。IRT将运动员能力和项目难度转化为统一的Logit单位,便于两者之间的比较。CTT假设裁判员的打分属于等距数据,但实际上这些得分是等级数据[3]。例如一个跳水动作,运动员将成绩从5.0提高到6.0要比从9.0提高到10分容易。从原始分数上看,同样是一分的差别,后者显然要付出更多的努力。IRT克服了CTT的这些缺陷,是对CTT的重要补充。已有研究者论证过将IRT用于运动技能的测量的可行性[4]。

技能类评分项目的得分受到运动员能力、时空条件(场地及出场顺序)、裁判等诸多因素的影响。通过CTT方法进行分析仅能得到运动员能力和裁判评分两方面的信息[5]。这些信息对运动员备战、裁判选拔来说有很高的价值,但却非常有限。而多面Rasch模型(many-Facets Rasch Model,MFRM)能将运动员能力、项目难度、裁判宽严程度、出场次序(回合)等因素统一在同一模型中,并转化为相同的Logit单位,方便因素间比较和交互作用分析。因此,本研究使用多面Rasch模型对伦敦奥运会男子10米台跳水决赛结果进行分析,以期为提高裁判水平、改进规则和运动备战提供参考。

2 研究对象及方法

2.1研究对象

MFRM研究所用数据取自2012年伦敦奥运会男子10米台跳水决赛。本场比赛共有12名运动员参加,分6轮进行,运动员的出场顺序按照半决赛成绩从低到高排列。共有7名裁判参加评分。评分规则规定运动员每一跳动作得分计算方式为：去掉两个最高得分、两个最低得分,计算剩余三个分数的平均分,再乘以动作的难度系数。MFRM分析使用的数据没有经过删除和加权,而是对全部打分数据进行分析。

本次研究所用的模型如下：

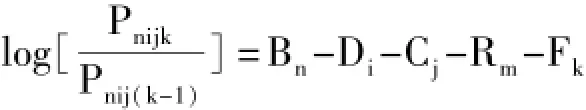
MFRM中每个影响因素为一个面,如运动员面、裁判面、动作面等。Pnijk是跳水运动员n在动作i上被裁判j评定为k分的概率,Pnij(k-1)是运动员n在动作i上被裁判j评定为k-1分的概率,P的取值范围为[0,1];Bn代表运动员n的能力,伦敦奥运会跳水决赛有12名(组)运动员参加,n=1,2,…,12;Di是动作难度,男子10米台跳水共出现14个动作,i=1,2,…,14; Cj是评委的宽严程度,共有7名裁判,j=1,2,…,7;Rm代表轮次难度,跳水决赛共有6轮,m=1,2,…,6;Fk是评分等级量表中从(k-1)到k分的等级难度。由公式可以见,如果运动员能力大于动作难度、裁判宽严程度、轮次难度、某一特定等级难度的和,那么他在该动作上获得该等级分数的概率大于50%。

MFRM分析结果除上述信息之外还包括偏差分析(Bias analysis)和交互作用分析(Interaction analysis)。偏差分析可以分析裁判给不同运动员打分时的宽严程度,为评价裁判评分的公平性提供参考。交互作用分析可以发现各面之间的交互作用,如轮次与裁判员之间的交互作用分析能够得到裁判员各轮次的宽严程度信息,为运动员备战、安排动作提供信息。

2.2数据分析

本研究使用FACETS 3.70软件,数据分析结果主要包括：层面图、运动员能力、裁判员宽严程度、动作难度、各轮次难度、评分量表中各等级难度等。

3 分析结果

3.1层面图

图1 层面图

层面图将不同层面的全部个体直观的呈现在同一Rasch量尺下,方便研究者了解各面个体的分布状况以及进行各面之间的比较。图1的最左侧为Rasch量尺,以Logit为单位。运动员面列出了能力估计的结果,中国运动员邱波能力最强,乌克兰运动员BONDAR Oleksandr能力最弱。轮次面显示第4轮、第5轮的竞争最为激烈。动作面显示5156B难度最高,207C难度最低。裁判面显示7号裁判打分最严格,3号裁判打分最宽松。评分面显示各等级分数梯难度之间不相等。

3.2运动员能力分析

MFRM在运动员能力估计过程中考虑了动作、轮次、裁判等因素,接近竞赛的实际情境,其能力估计结果更接近运动员实际水平。

MFRM各面的参数估计结果包括：属于该面每个个体的参数(Measure)、参数估计误差(Model SE)、拟合参数(Infit MNSQ、Outfit MNSQ、ZStd、RMSE)、分离系数(Separation)和分离信度(Separation Reliability)。

以运动员能力估计为例(见表1),估计结果为转化后的数据,以Logit为单位;参数估计误差反映能力估计的精准程度。Infit MNSQ和Outfit MNSQ反映了模型预期与实际观测值间的差异,理想值为1[6]。Outfit MNSQ是未加权的拟合统计量,受偏离模型预期的极端数据影响较大,Infit MNSQ是加权后的拟合统计量,受极端数据影响较小。一般将Infit MNSQ作为拟合参数。这两个拟合统计量在[0.6,1.4]区间较好[7]。运动员能力估计的拟合参数大于1.4,表明其可能出现超常或失常发挥。12名运动员中第8名WOLFRAM Martin、第12名BONDAR Oleksandr的Infit MNSQ大于1.4,可能出现超常发挥或失常发挥。分离系数反映了属于同一面的个体之间差异程度,大于2就认为个体之间存在显著差异[8]。运动员面的分离系数为7.12,表明运动员之间的能力差异显著。分离信度是真实变异与观测变异之比,理论范围为[0,1],运动员面的分离信度为0.98,表明Rasch分析的结果可靠性很高。

表1中运动员以能力高低排序,决赛排名与Rasch分析结果之间存在显著相关(r=0.902,p＜0.001),但在关系金牌归属的关键名次上存在差异。出现这一差异的原因可能在于计分规则。奥运会比赛的成绩是删除4个评分后求平均分并乘以难度系数加权的结果。删除4个裁判的评分丢失了大量信息,这就人为加大了能力估计的误差。使用剩余评分的数据进行能力估计,结果显示能力估计的平均误差为0.28,而使用全部评分数据进行能力估计时的平均误差仅为0.14。

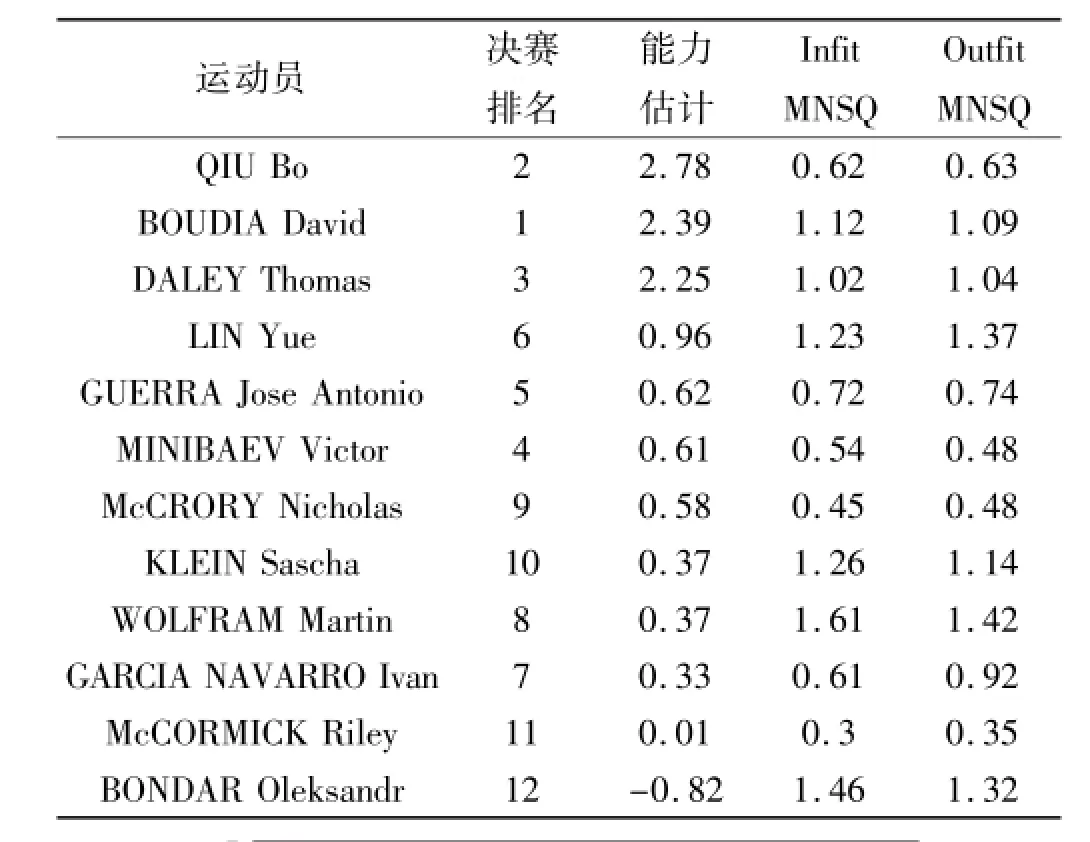
表1 运动员能力估计结果

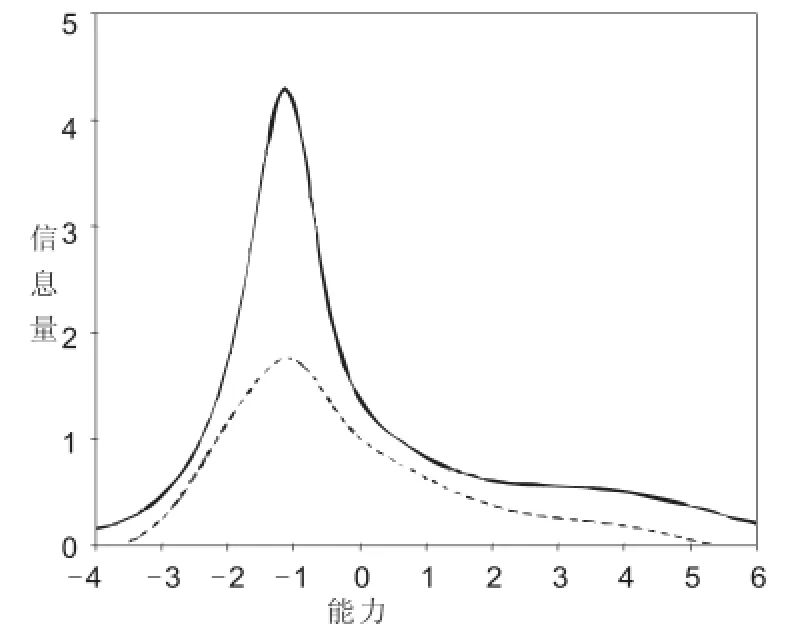
图2 信息量图

项目反应理论中提出了“信息量”的概念来表示测量的精准程度[9]。比较两种情况下的信息量,发现删除4个评分后的信息量(虚线)不足删除前(实线)的一半(见图2)。这表明奥运会的评分规则导致大量的有效信息被删除,对评分结果的公平性、准确性影响很大。删除部分评分的初衷是为了避免极端评分对比赛结果的影响,但也可能会出现下述情况。第1轮中GUERRA Jose Antonio和McCORMICK Riley均选择了107B,两人的得分情况见表2。按照评分规则,GUERRA Jose Antonio的评分中删除两个最高分9.0、9.0和两个最低分8.5、8.5;McCORMICK Riley的得分应删除两个最高分8.5、8.5和两个最低分8.0、8.0(见表2)。删除后两名运动员得分相同(平均8.5,最终得分=平均分8.5×难度系数3.0=25.5)。但从总体情况看,GUERRA Jose Antonio能力明显高于McCORMICK Riley。Rasch的分析结果与原始的得分情况一致,GUERRA Jose Antonio能力更高。出现类似情况时,奥运会的评分规则不能区分两人的能力差异。

表2 两名运动员第1轮得分

3.3裁判评分分析

裁判的主观评分过程受到心理、生理、环境等多种因素的影响,自身的宽严标准会有波动;裁判之间的宽严程度也会有所差异。这种同一评分者前后宽严标准不统一,不同评分者之间宽严标准不统一的现象称为评分者效应[10]。在重大比赛的裁判工作中,这些波动和差异对比赛结果影响很大。

裁判评分的分析结果表明,7号裁判打分最严格,3号裁判打分最宽松。裁判之间宽严程度的极差为0.28(Logit单位),标准差0.09。裁判面的分离系数小于0.01。裁判之间宽严程度不存在差异,裁判对评分尺度的把握非常统一。

裁判宽严标准的拟合参数大于1.4,表明其打分比较激进,完成好的动作打分很高、完成差的动作打分很低,分数之间差异很大。相反,拟合参数小于0.6则表明其打分比较保守,存在趋中现象,完成好的动作给分偏低,完成差的动作给分偏高。1号裁判为12名运动员打分的标准差为1.03,在全部裁判中最高。该名裁判的Infit MNSQ=1.35,说明其打分时最为激进。2号裁判打分的标准差为0.73、极差3.5,在所有裁判中最低,Infit MNSQ=0.74,说明其打分较保守。尽管如此,所有裁判的拟合参数都在可以接受的范围之内。

除评分宽严程度之外还可以对裁判掌握评分量表的情况进行分析。奥运会的评分属于等级评分,以0.5为一个等级。裁判根据运动员动作完成情况,按照规则要求,从0-10分中选择自己认为合适的分数。Rasch理论要求,运动员能力越高得分等级越高,且等级量表中相邻两个分数等级的间距应当相等[11]。但实际应用中,等级间距相等这一要求很难满足。各评分等级的参数见表3。等级间距不相等,意味着原始分数相差一个等级(0.5分),体现出来的实际能力差距有所不同。如得10分的运动员得分高出得9.5分的运动员一个等级,实际能力高出0.57个Logit单位;得7.5分的运动员得分高出得7分的运动员一个等级,实际能力仅高出0.28个Logit单位。Rasch理论要求,等级越高,对应的能力越高。5.0、6.0、6.5三个等级出现了倒置现象,即高能力对应低等级、低能力对应高等级。如能力为-0.74的被试得分为5.5分,比他能力低的被试(能力为-0.87)得分为6.0或6.5。这说明裁判对这三个等级把握不准确。这对改进裁判工作、提高裁判水平很有价值。

3.4轮次难度分析

奥运会跳水决赛中运动员每轮出场一次,每次做一个动作,共需完成6轮比赛。出场时间以预赛成绩排序,这就为比赛增加了时间因素。了解各轮次的难度对运动员的备战有很大帮助。

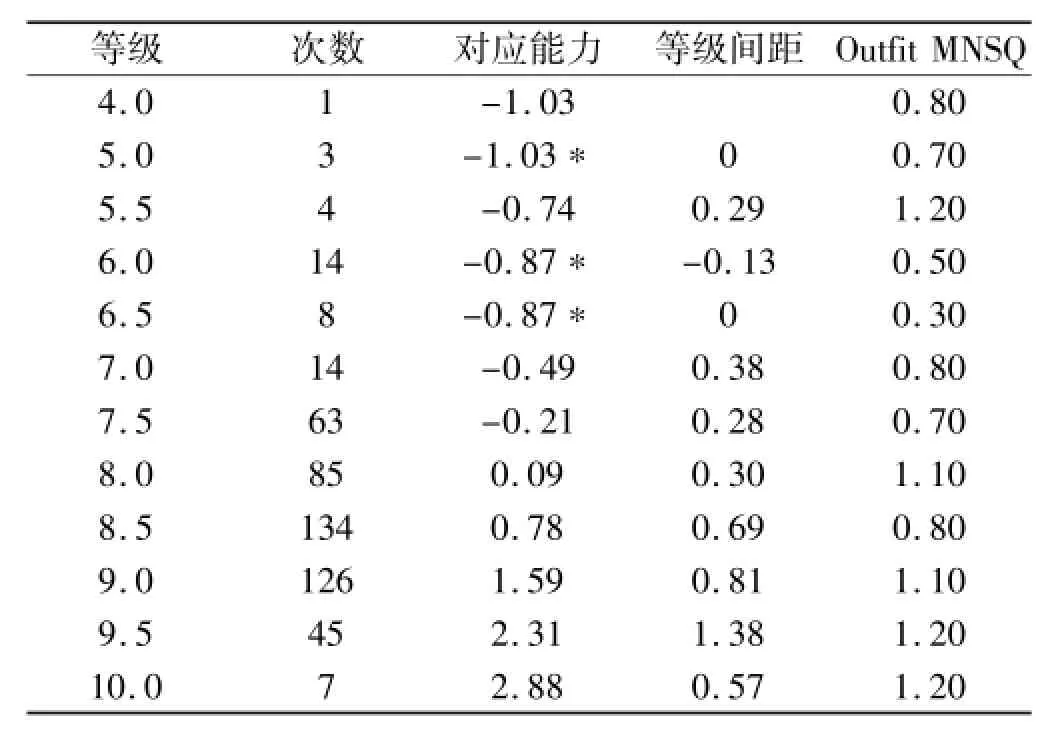
表3 等级评分分析

数据分析结果表明,比赛的中后阶段竞争非常激烈。难度最高的两轮为第4轮、第5轮。这两轮中12名运动员得分的标准差最大,分别为11.17和11.34,说明运动员发挥差异很大。运动员之间拉开距离主要是在第4轮、第5轮。轮次面的分离系数为6.31,分离信度0.98,表明各轮次难度存在显著差异。

3.5动作难度分析

动作的难度系数由国际游泳技术委员会规定,在计分过程中,难度系数以权重的形式出现,是确定奥运会最终成绩的重要因素。本次决赛,12名运动员共使用了14个动作,Rasch难度估计结果见表4。

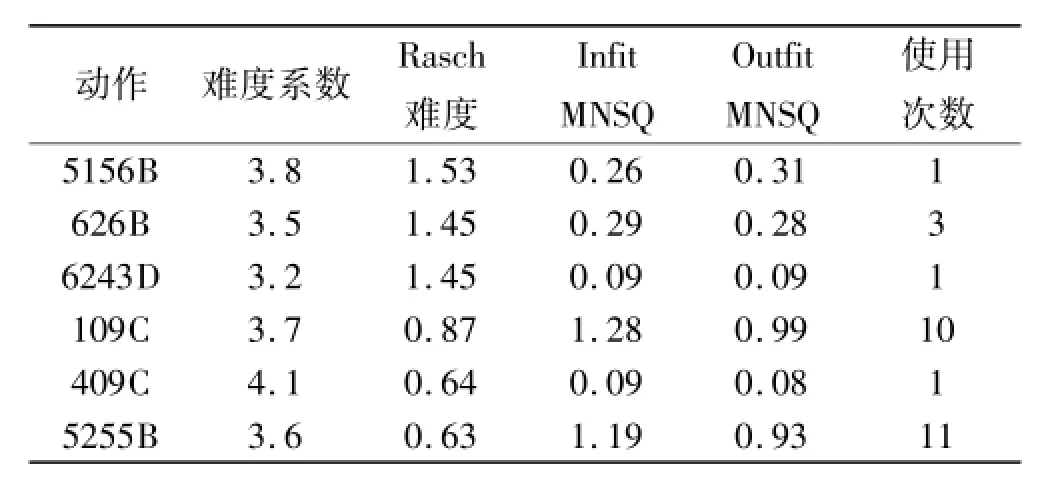
表4 动作难度分析

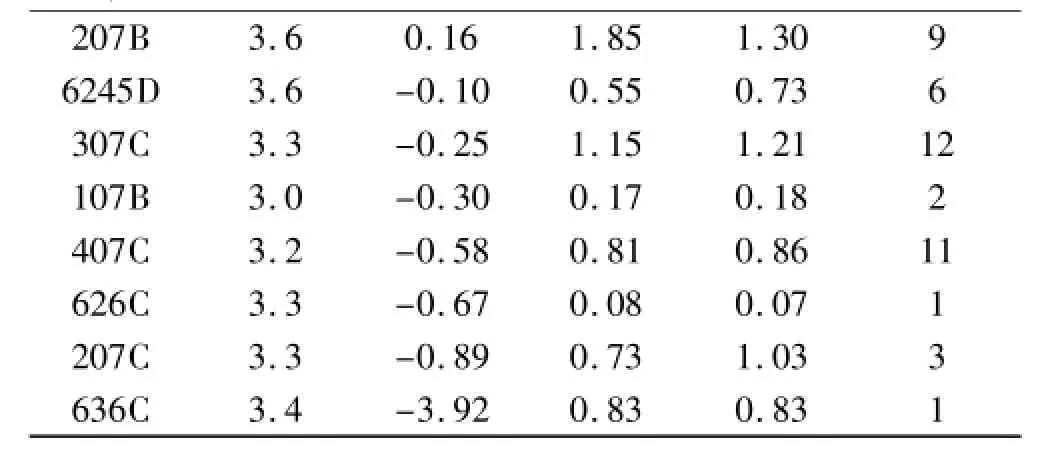
续表4

14个动作按Rasch难度排序与规则规定的难度系数排序之间有所不同。有些高难度系数动作(409C,难度系数4.1)的Rasch难度估计为中等,有些低难度系数动作(6243D,难度系数3.2)的Rasch难度较高。这些信息对运动员备战很有价值：运动员可以选择409C这类难度系数较高但Rasch难度较低的动作,尽量避免选择6243D这类难度系数较低但Rasch难度较高的动作。

动作难度面的分离系数为5.86,分离信度0.97,表明运动员对各动作的掌握存在显著差异。

3.6交互作用分析

对影响结果的各面之间交互作用进行分析可以得到更多比赛信息。

运动员与轮次之间交互作用的分析结果为比赛中运动员状态的保持和调整提供了参考。图3将各轮次按难度从左至右、由低至高排列,可以发现运动员比赛中状态起伏不定,不同运动员状态起伏特点不同。两名中国运动员,前两轮均发挥出色。邱波在第4轮、第5轮表现较差,林跃后四轮发挥均不理想。最终夺冠的BOUDIA David第3、4、6轮发挥出色。同时还发现中国运动员邱波的表现最为稳定,他的Rasch能力也最高。Rasch能力排名第2、第3的BOUDIA David和DALEY Thomas发挥不稳定,尤其在难度较低的1、2两轮表现很差。

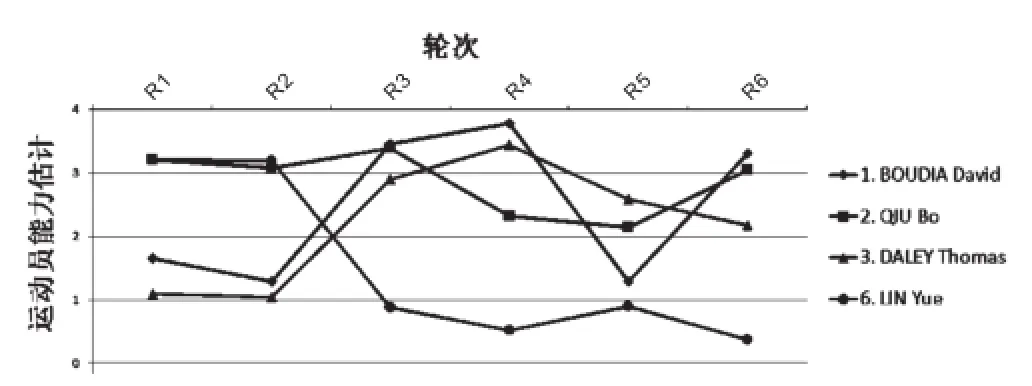
图3 运动员与轮次交互作用分析

运动员与裁判之间交互作用的卡方检验结果表明裁判与运动员之间不存在交互作用,裁判的打分客观公正。比赛过程中,英国选手DALEY Thomas曾申请重跳,以上Rasch分析都是基于重跳后的打分。该选手得分数据分析中并未出现与模型不拟合的异常值。对其重跳前的打分结果进行分析,发现1、2、4、5、7号裁判的打分均为异常值。也就是说该名运动员第一次试跳发挥失常,重跳对其得分和名次有重大影响。

裁判与轮次之间交互作用的卡方检验结果表明裁判员各轮次打分的宽严标准一致,多数裁判能够保持自己评分的宽严程度一致。只有3号裁判的宽严程度波动较大,尤其是在第1轮时,打分较宽松。这种波动在模型允许的范围之内,未对比赛结果产生影响。

4 讨论

4.1参数估计结果对规则修订的启示

Rasch分析得到的运动员能力排序与实际比赛结果相关显著,但在关键名次上有差异。对评分规则的分析发现：现行的评分规则采取的去掉最高和最低各两个评分方法使得大量的有效信息被删除。导致比赛成绩的代表性差,比赛结果的随机性增大。运动员能力估计的误差增大,尤其是在运动员能力相近时,不能有效区分。更有可能导致关键名次上的排序与实际能力不符,造成争议。同时,删除数据的计算方法对裁判心理也会产生影响。

优质的评分规则应能准确、快速评价运动员能力,同时计算简单、便于推广。与奥运会规则相比,Rasch理论提供的能力估计方法能够更加准确的评价运动员,但因为理论复杂,不适合推广。在制定或修订规则时可选择现代测量理论进行充分论证,确保评价结果准确、公正。

对裁判评分的分析可以有效避免评分时的舞弊现象,也可以了解裁判员掌握规则的程度。这一方法在裁判员的培训及选拔过程中可以发挥重要的作用。

4.2交互作用对运动员备战的启示

对运动员能力分析可以发现运动员在不同轮次上发挥起伏的规律。以中国运动员为例：邱波的表现比较稳定,但第4轮、第5轮表现欠佳。两轮选择的动作为207B和109C,在其选择的所有动作中难度较高。由于其本身的发挥规律,在比赛中段或难度较高时表现会有起伏。刚好本次比赛这两个动作安排在比赛中段,导致其得分不理想。

收集运动员参加世界大赛的数据进行分析,可以总结出其运动规律。制定竞赛策略时,应当综合考虑运动员自身运动规律、动作难度、裁判员打分规律。这样针对比赛出现的问题进行的备战,将会帮助提高运动员的成绩。

4.3动作难度对制定比赛策略的启示

比赛的规则应当与运动的发展相适应,以本次分析为例：跳水动作Rasch难度与规则规定的难度系数之间存在差异。国际泳联可以将现代测量理论分析结果作为修订规则的参考。从备战及比赛策略的角度来讲,运动员比赛中可以选择Rasch难度低但难度系数高的动作,这样更有可能得到高分。以109C为例,规则中动作的难度系数为3.7,是决赛出现的全部动作中难度系数最高的动作之一。但这一动作的Rasch难度仅为0.87,在所有动作中,Rasch难度属于中等稍高水平。选择这一动作可以在实际难度较低的情况下获得较高的权重,从而在得分上获取一定的优势。

以Rasch为代表的项目反应理论在比赛成绩确定、规则修订、评价裁判评分的客观性等方面都有很强的应用价值。在今后的研究和应用中应当将现代测量理论与传统方法相结合,才能得出更有价值的结论。

5 结论

(1)对裁判评分的分析表明,总体上讲裁判的评分公平、公正,未出现舞弊现象;但裁判员对个别评分等级把握不准确。

(2)动作Rasch难度分析结果与规则规定的难度系数存在差异。

(3)对评分规则的分析发现：现行的评分规则采取的去掉最高和最低各两个评分方法使得大量的有效信息被删除,增大了测量误差。

(4)对运动员能力的分析发现Rasch能力估计与比赛名次相关显著,但在关键名次上存在差异。

以Rasch理论为代表的现代测量理论可以运用到体育心理学领域,分析结果为提高裁判水平、改进规则和运动员备战提供了丰富的信息。

[1]魏高峡,李佑发,孙晓敏.概化理论及其在运动成绩主观评定中的应用[J].北京体育大学学报,2006,29(1)：53-55.

[2]魏登云.主观评分误差的非参数处理方法[J].中国体育科技,2001(3)：39-41.

[3]漆书青,戴海崎,丁树良.现代教育与心理测量学原理[M].北京：高等教育出版社,2002：79-82.

[4]张军.项目反应理论在体育运动领域的应用——运动项目主观评分和比赛排名的量化[J].体育成人教育学刊,2008(3)：38-41.

[5]俞宗火,唐小娟,王登峰.GT与IRT的比较：北京奥运会男子10米跳台跳水分析[J].心理学报,2009(8)：773-784.

[6]姚若松,赵葆楠,刘泽,等.无领导小组讨论的多侧面Rasch模型应用[J].心理学报,2013(9)：1039-1049.

[7]Wright B D,Linacre JM,Gustafson J E,et al.Reasonable mean-square fitvalues[J].Raschmeasurement transactions,1994,8(3)：370.

[8]Guilford J P.Fundamental statistics in psychology and education.[M].New York,NY,US：McGraw-Hill,1942：13.

[9]罗照盛.项目反应理论基础[M].北京：北京师范大学出版社,2012：88-91.

[10]Wolfe E W.Identifying rater effects using latent traitmodels [J].Psychology Science.2004,46：35-51.

[11]刘国庆,赵守盈.Rasch模型在李克特量表中的应用[J].贵州师范大学学报(自然科学版),2012(1)：13-16.

Multi-Faceted Rasch Analysis of Result of Skill Referees of Sport Events——Application of item response theory in sport filed

HE Zhuang,et al
(Faculty Of Education,Beijing Normal University,Beijing,100875)

This paper analyzes the results ofMen's10meter platform diving at the London Olympic Games by using themethod of Multi-Faceted Rasch Model.The results indicate that there are differences between the ranks of athletes' ability and the result of Olympic Games.The athletes'forms are unstable during competitions.The referees abide by the same judging standards but they are subject to inaccuracy in some grading levels.There is a certain gap between the difficulty degree and that of the Rasch analysis.The data from Rasch analysis can provide references for the selection of referees,rule amendment and athletes'preparation for competitions.

mufti-faceted Rasch Model;item response theory;diving;subjective assessment

G808

：A

：1001-9154(2014)03-0043-06

G808

：A

：1001-9154(2014)03-0043-06

何壮(1984-),男,山东聊城人,在读博士研究生,研究方向：教育测评。

赵守盈。

2013-12-04