三角形课程难度的定量分析比较

陈丹媛　张磊

摘 要： “三角形”是最基本的几何图形，在我国初中数学课程体系中有着非常重要的作用.2011年的《全日制义务教育数学课程标准（实验稿）》与2000年的《全日制九年义务教育初中数学教学大纲（试用修订版）》中对三角形的教学要求相比，发生了很大的变化.本文利用课程难度定量模型N=αG/T+（1-α）S/T，对我国初中阶段“三角形”的课程难度进行定量分析和比较，总结出一些值得广大数学教师共同关注的变化与调整.

关键词： 三角形 课程难度 可比深度 可比广度 课程时间

一、问题的提出

2011年的《全日制义务教育数学课程标准（实验稿）》[1]（以下简称《标准》）与2000年的《全日制九年义务教育初中数学教学大纲（试用修订版）》[2]（以下简称《大纲》）中的几何内容相比，发生了较大的变化.这些变化对初中数学教师理解和实施《标准》提出了挑战.与《大纲》相比，《标准》中的几何内容难度有何变化？本文利用刻画课程难度的数学模型，对《标准》与《大纲》中三角形的难度进行定量分析和比较，探讨几何课程难度变化给学生发散思维能力和推理能力发展带来的影响.

二、课程难度模型的注释

据东北师范大学史宁教授对课程难度的研究方法，他们对概念的界定是[3，4]：影响课程难度的基本要素至少有三个：课程深度、课程广度和课程实施时间.其中，课程深度是指课程内容所需要的思维的深度，可以用课程口标要求的不同程度来量化；课程广度是指课程内容涉及的范围和领域的广泛程度，可以用知识点的数量来量化；课程实施时间是指完成课程内容所需要的时间，可以用“课时”来量化.也就是说，课程难度可以看成是关于课程广度、课程深度、课程实施时间的一个函数，其中任何一个量的变化均会引起函数值，即课程难度的变化.

显然，课程难度与课程深度、课程广度成正比，与课程实施时间成反比.因此，可以用单位课时下课程的广度和课程的深度衡量课程难度，前者被称为课程的“可比广度”，后者被称为课程的“可比深度”.这样，课程的可比广度与可比深度越大，这门课程越难.但有一个侧重程度，即需要考虑课程的可比广度和课程的可比深度哪个对课程难度的影响大.因此，课程难度可以看成是“可比广度”和“可比深度”的加权平均值.

如果用N表示课程难度，用S表示课程深度，用G表示课程广度，用T表示课程时间，综上所述，可以建立刻画数学课程难度的模型如下：

N=αG/T+（1-α）S/T（1）

其中G/T表示可比广度，S/T表示可比深度，α称为加权系数，0<α<1，是一个经验性常数，反映了可比广度、可比深度对课程难度影响的侧重程度.

三、《标准》与《大纲》中三角形的难度量化比较

（一）课程时间

对于《标准》，在“人教版”[5]中：八年级上册第11章“三角形”中出现“与三角形有关的线段”、“与三角形有关的角”是6课时，第12章“全等三角形”是11课时，第13章“轴对称”中出现“等腰三角形”是5课时；八年级下册在第17章“勾股定理”是9课时；九年级下册在第27章“相似”中出现“相似三角形”是7课时，第28章“锐角三角函数”中是12课时，共计50课时，于是T■=50.

而在《大纲》下的教科书中安排45课时，于是，T■=45.

（二）课程广度

《标准》中三角形的知识点分布较散，相应课程内容的知识点合计41个，取综合的课程广度系数G■=41.考虑到“图形与变换”在《大纲》中出现在《三角形》之中，并且仅出现轴对称，相应课程内容的知识点合计39个（不含选学内容“反证法”），取综合的课程广度系数为G■=39.

（三）课程深度

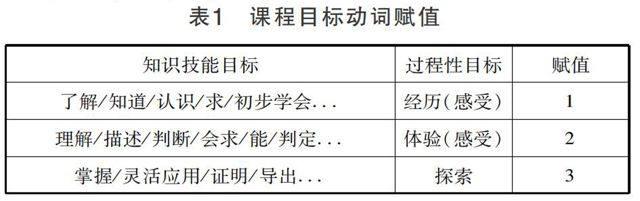
《大纲》中是按四个层次“了解”“理解”“灵活应用”陈述目标（要求）的，《标准》中则是按三个层次陈述目标（要求）的。考虑到“掌握”这一要求与“灵活应用”区别并不是很大，为了与《标准》中的层次对应，将“掌握”与“灵活应用”合并为同一个层次，则对《大纲》和《标准》中过程性目标赋值如表1.

表1 课程目标动词赋值

（四）课程内容要求的对比

1.《标准》中“三角形”相应课程内容的知识点对应的课程深度值分别如下。

（1）概念部分

三角形（包括三角形顶点、边、内角、外角、角平分线、中线和高）：2；全等三角形：2；等腰三角形：1；直角三角形：1；三角形重心：l；三角形的内心、外心：1；相似三角形：1；锐角三角函数：2.

（2）定理部分

三角形的稳定性：1；三角形内角和定理：3；三角形的边长关系：3；三角形外角和定理：3；三角形中位线定理：3；三角形全等判定SAS：3；三角形全等判定ASA：3；三角形全等判定AAS：3；三角形全等判定SSS：3；等腰三角形性质定理：3；等腰三角形判定定理：3；三线合一定理：3；等边三角形性质定理：3；等边三角形判定定理：3；直角三角形的性质定理：3；直角三角形全等判定：3；勾股定理：3；勾股定理的逆定理：3；三角形的中位线定理：3；三角形相似的判定定理：1；三角形相似的性质定理：1.

（3）技能部分

作三角形的角平分线、中线和高：2；作等腰三角形的对称轴：2；三边作三角形：2；两边及其夹角作三角形：2；两角及其夹边作三角形：2；底边及底边上的高作等腰三角形：2；一直角边及斜边作直角三角形：2；30°，45°，60°的三角函数：l；解三角形：2；用计算器求锐角三角形函数值：2；求三角形函数值对应的锐角：2；作三角形的内切圆：2.

2.《大纲》中“三角形”相应课程内容的知识点对应的课程深度值分别如下。

（1）概念部分

三角形（包括三角形顶点、边、内角、外角、角平分线、中线和高）：1；全等三角形：l；三角形的内心、外心：1；相似三角形：2；相似比：2；锐角三角函数：1.

（2）定理部分

三角形的稳定性：1；三角形内角和定理：3；三角形的边长关系：2；三角形外角和定理：3；三角形中位线定理：3；三角形全等判定SAS：3；三角形全等判定ASA：3；三角形全等判定AAS：3；三角形全等判定SSS：3；等腰三角形性质定理：3；等腰三角形判定定理：3；三线合一定理：3；等边三角形性质定理：3；等边三角形判定定理：3；直角三角形的性质定理：3；直角三角形全等判定：2；勾股定理：3；勾股定理的逆定理：2；三角形的中位线定理：3；三角形相似的判定定理：3；三角形相似的性质定理：2.

（3）技能部分

作三角形的角平分线、中线和高：2；作等腰三角形的对称轴：2；三边作三角形：2；两边及其夹角作三角形：2；两角及其夹边作三角形：2；底边及底边上的高作等腰三角形：2；一直角边及斜边作直角三角形：2；30°，45°，60°的三角函数：l；解三角形：2；用计算器求锐角三角形函数值：2；求三角形函数值对应的锐角：2；作三角形的内切圆：2.

3.与《大纲》相比，《标准》中“三角形”课程内容要求的变化。

（1）概念部分

对“三角形（包括三角形顶点、边、内角、外角、角平分线，中线和高）、全等三角形、锐角三角函数”三个内容的难度要求从了解提高到理解，而对“相似三角形”，则从理解降低到了解；增加“等腰三角形、直角三角形、三角形重心”三个内容，并要求理解；删除原本要求理解的“相似比”.

（2）定理部分

对“三角形的边长关系、直角三角形全等判定、勾股定理的逆定理”三个内容的难度要求，从理解提高到掌握，而对“三角形相似的判定定理”、“三角形相似的性质定理”，则分别从灵活运用、理解降低到了解.

（3）技能部分

分别增加会作“作三角形的外接圆”，删除原本要求会作“作三角形的角平分线、中线和高”的技能要求.

（五）难度比较

根据以上数据，分别求出《标准》与《大纲》中三角形部分的可比广度、可比深度[6]，统计数据及比较结果如表2所示：

表2 《标准》与《大纲》中三角形部分的数据统计结果

注：右上角的数字分别代表与《大纲》中三角形相比，《标准》中三角形的可比广度与可比深度的变化，用“+”代表增加，用“-”代表降低.

1.根据所建立的数学模型N=αG/T+（1-α）S/T，分别表示出《标准》与《大纲》中三角形部分的课程难度：

四、结论

从以上统计数据可以看出，课程实施时间、课程广度、课程深度三个量当中的任何一个有微小变化，都会引起课程难度的变化.分析上述表格的数据，可以发现，《标准》下的《大纲》下的《大纲》下的《三角形》内容基本一致.《标准》下的《三角形》课程难度有所降低，主要原因是《标准》中该部分内容的课程广度和课程深度增加不大，但课程实施时间增加较大，使其可比广度和可比深度分别降低了0.05和0.14.也就是说如果时间充足的话，可比广度和可比深度也会有所降低.

这启示我们，如果课程实施时间较长，课程难度就会大大降低.也就是说，时间允许的话，完成《标准》中很多的探索对学生更好地掌握知识有很大的帮助，从而培养学生的发散思维能力和推理能力.

参考文献：

[1]中华人民共和国教育部.全日制义务教育数学课程标准（实验稿）[M].北京：人民教育出版社，2011.

[2]中华人民共和国教育部.全日制九年义务教育初中数学教学大纲（试用修订版）[M].北京：人民教育出版社，2000.

[3]吕世虎，史宁中，陈婷.《标准》与《大纲》中几何部分内容难度的比较研究[J].课程·教材·教法，2006（8）：38-43.

[4]史宁中，孔凡哲，李淑文.课程难度模型：我国义务教育几何课程难度的对比[J].东北师人学报（哲学社会科学版），2005（6）：151-155.

[5]课程教材研究所.义务教育教科书.[M].北京：人民教育出版社，2013.

[6]李高峰.课程难度模型运用中的偏差及其修正—与史宁中教授等商榷[J].上海教育科研，2010.3：46-49.

基金项目：2014年广东省大学生创新创业训练计划项目：基于课程难度定量分析模型下的初中几何课程难度研究，项目编号：201410578047。