基于SPSS软件的双语试卷质量与学生成绩定量分析

王本洋 唐 松 徐正春

（华南农业大学林学院，广州 510642）

双语教学是我国教育改革的一个亮点，双语教学研究也因此成为我国教育研究的一个热点。英国《朗文语言教学及应用语言学辞典》（Longman Dictionary of Language Teaching &Applied Linguistics）对双语教学（Bilingual Education）的定义是the use of a second or foreign language in school for the teaching of content subject，即在学校里使用第二语言或外语进行学科教学。我国《双语教学示范课程建设项目评审指标体系》中指出，双语教学是指将母语外的另一种外国语言直接应用于非语言类课程教学中，并使学生同步获取外语和学科知识的一种教学模式。

试卷分析是考试之后的一项重要工作，其结果是对考试工作进行总结并给予恰当评价的重要依据［1］。试题质量是保证考试成绩客观反映学生的知识、能力和素质状况的关键［2］。教师通过对试卷进行分析，评价试题的难易程度，改善和提高试题的质量，并发现教学过程中的不足，改进教学方法，提高教学质量［1］。

试卷分析包括试卷成绩分析和试卷质量分析2部分［3-4］，但多数文献重点研究了试卷质量的分析及其计算方法［1，5-11］，对统计软件在试卷分析中的应用介绍不多［3，4，12］，对学 生成绩 的后续 分析尚 未深入。张瑶等［13］利用层次聚类和关联规则技术对学生试卷进行分析，得到特定题目知识点之间的相关性。谭庆［14］将关联规则Apriori算法应用于试卷成绩分析中，挖掘学生各科目成绩的优良影响关系，并产生关联规则。谭庆［15］、张晓翊等［16］将k-means聚类算法应用于试卷成绩分析中，对学生试卷成绩进行类别划分。

SPSS软件广泛应用于经济学、生物学、教育学、心理学等领域，是与SAS、BMDP 齐名的3 大统计软件之一。其用户界面友好，通过菜单操作即可实现绝大部分统计分析功能。本研究借助SPSS 13.0软件，在综合运用基本描述性统计指标和4度指标评价试卷质量的基础上，运用方差分析方法，实现对“旅游礼仪礼节”双语课程某次考试的试卷质量及学生成绩的定量分析，为更好地开展双语教学工作提供参考。

一、材料与方法

（一）材料

数据来自华南农业大学双语选修课程“旅游礼仪礼节”一次考试的试卷。其试题均以英语形式出现，考生可选用中文回答的试题约占50%。试卷分4个大题，满分100分，第一题（Part1）为选择题，占20分；第二题（Part2）为判断题，占20 分；第三题（Part3）为名词解释题，占20 分；第四题（Part4）为简答题，占40 分。考生由2008级旅游管理专业5个班级（A～E）中选修该课程的学生组成，人数为106人，其中男生20人，女生86人。

由于试卷质量直接影响成绩分析的有效性，因此本研究先分析试卷质量，然后再分析学生的成绩。

（二）试卷质量分析

试卷定量分析常用4度指标（即难度、区分度、效度和信度）来进行，这是统计学方法在科学分析考试中的一种应用［1］。任汉斌和单蓉［11］以教育统计与测量理论为基础，根据学生考试原始成绩，用4度指标构建了试卷质量分析的数学模型。安萍莉等［2］选择平均成绩、标准差、全距、众数、偏度、峰度、平均难度等作为分析指标，分别从横向的基础课、专业基础课、专业课和纵向的不同年份进行对比分析，对各门课的考试成绩进行了研究。

根据“旅游礼仪礼节”双语课程的特点，该次试卷质量分析的主要指标有12个，分为2类：一类是考试成绩的基本描述性统计指标，包括成绩的均值（Mean）、最 小 值（Min.）、最 大 值（Max.）、全 距（Range）、标 准 差（Std.Dev.）、峰 度（Ku.）、偏 度（Sk.）和成绩分布正态性等8个指标；第2类是4度指标，各个指标的原始模型参见文献［1-2，5，8，10］，SPSS软件操作参见文献［3-4］。

1.难度

2.信度

采用克朗巴哈α值（Cronbach′s Alpha）计算信度，，其中，分别表示第i题和总分的方差。

3.效度和区分度

用Pearson相关系数r表示效度（x，y 均为题目得分）和区分度（x，y 其中一项为题目得分，另一项为总分）。

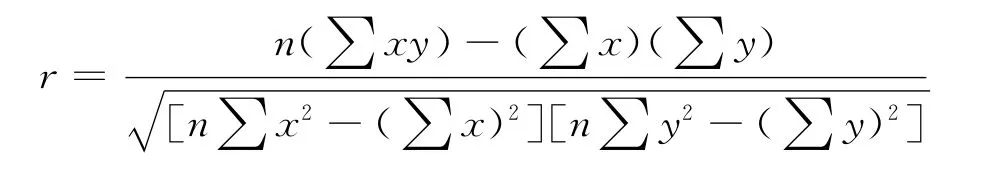
（三）学生成绩分析

借助方差分析［17］方法考查学生的考试成绩，通过对组间差异与组内差异的比值分析来综合性地确定多组平均数差异的显著性。当组间和组内方差的F 检验结果有显著性差异时，需要对各对平均数进行差异性检验（即多重比较）和方差齐性检验。

当方差分析要求的条件不满足时，可使用非参数检验方法。非参数检验不要求总体满足正态性和方差齐性等条件。另外，对几个独立样本差异的显著性，可用Kruskal-Wallis检验，它相当于对多组平均数进行的非参数的方差分析［17］。

二、结果与分析

（一）基本描述性统计指标

成绩的基本描述性统计数据，见表1。D 班的表现与其他班有差异，其平均成绩低于总体平均值，全距（27）和标准差（8.684）均为最大。

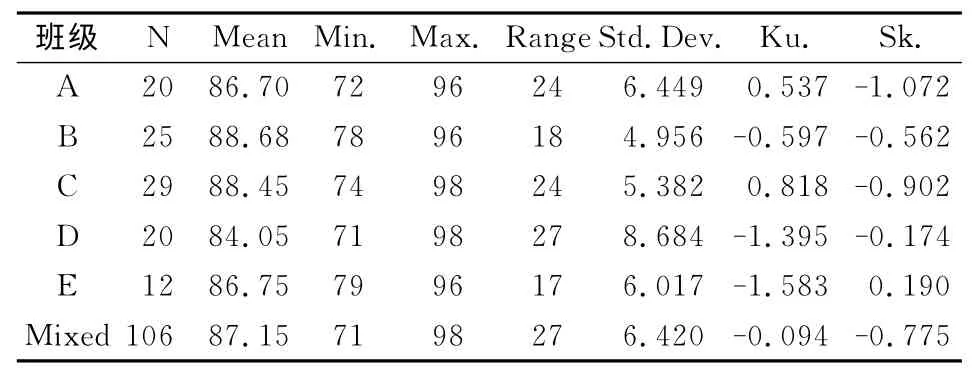
表1 成绩的基本描述性统计指标

成绩分布的正态性检验，见表2。从表2看，有4个班（B、C、D 和E）的成绩符合正态分布（Sig.＞0.05），A 班和混合班的成绩不符合正态分布（Sig.＜0.05）。

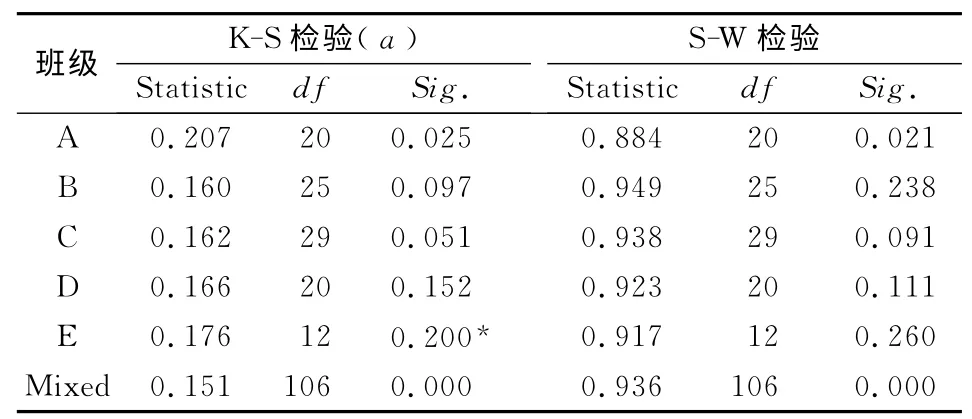
表2 成绩分布的正态性

（二）“4度”指标

1.难度

从试卷难 度看，D 班最大（0.16），B 班最小（0.11）；从试题难度看，题三（Part3）最大，且在D 班最大（0.38），B班最小（0.18）。总体上，该套试卷不难（难度0.13＜0.2），仅题三（Part3）的难度较大（难度0.24），见表3。

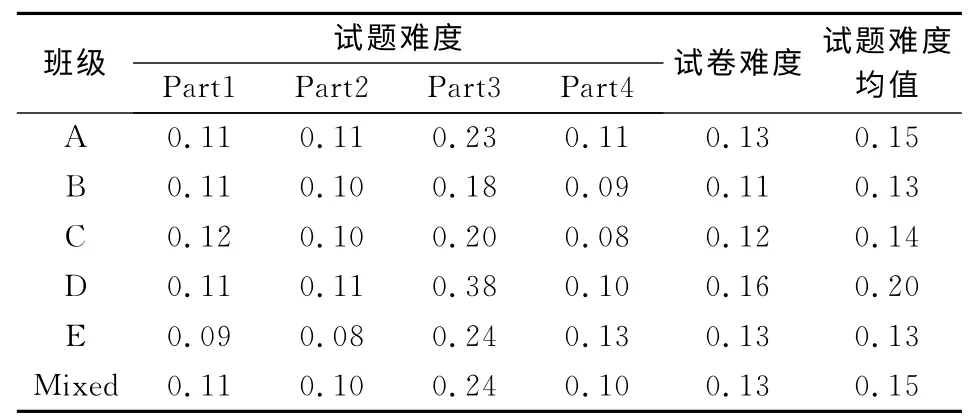
表3 试卷难度

难度分析表明，同一套试卷在不同班级表现出不同的难度，不同题目的难度也存在一定差异。另外，试题难度均值稍大于试卷难度。因此在仅知道各试题难度的情况下，可用其均值估算试卷难度。

2.信度

信度分析结果表明，该套试卷的信度值为0.995。

3.效度和区分度

该套试卷各题目之间的相关系数，见表4，仅题三（Part3）与题四（Part4）间为0.266，其余均小于0.2，说明该套试卷的效度较高。该套试卷各题与总分之间的相关系数，仅题一（Part1）与总分（Total）之间为0.293，其余均大于0.4，其中题三（Part3）与总分（Total）之间达0.743，说明该套试卷的区分度较高。

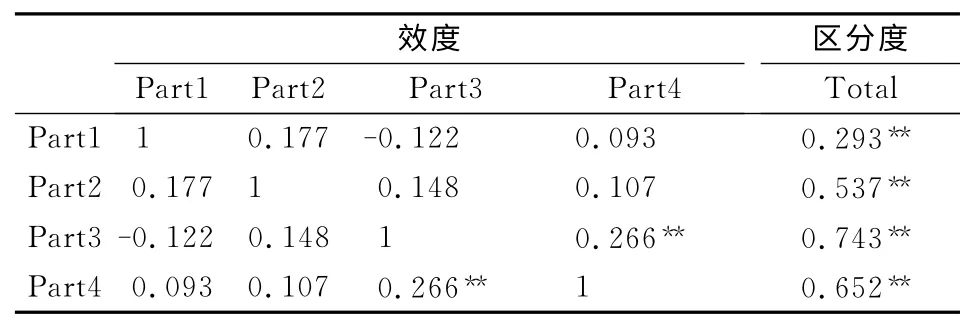
表4 相关系数的效度和区分度

（三）学生成绩分析

1.完全随机设计的方差分析

SPSS软件设计模型为Intercept+Class+Gender+Class＊gender，即检验班 级（Class）、性 别（Gender）以及班级与性别间交互效应（Class＊gender）对成绩的影响。

方差分析结果表明，班级与性别间无交互效应（Sig.=0.791＞0.05）。Levene检验结果表明，F=3.130，Sig.=0.002＜0.05，表明方差不齐。在此前提下基于Games-Howell进行的Post Hoc分析表明，5 个班级间的成绩没有显著性差异，见表5。

表5 完全随机设计的方差分析

2.嵌套设计的方差分析

SPSS 模型为Intercept+Class+Gender（class）。在班级与性别间无交互效应条件下，考虑到不同班级的不同性别间可能存在显著性差异，因此把班级（Class）作为一级因素，性别（Gender）作为二级因素，检验两个因素对成绩的影响。

方差分析表明，不同班级（Sig.=0.112＞0.05）及其不同性别（Sig.=0.360＞0.05）间的成绩无显著性差异，见表6。

表6 嵌套设计的方差分析

3.非参数检验

根据前述分析，方差分析的前提条件方差齐性不满足。因此改用非参数方法检验班级、性别对成绩的影响。Kruskal-Wallis检验表明，不同班级的成绩间没有显著性差异（Sig.=0.359＞0.05），不同性别间的成绩有显著性差异（Sig.=0.022＜0.05）。因此，根据成绩基本描述性统计指标得到的结论，即D班与其他班有差异，并不具有统计学意义，见表1。

进一步分析表明，平均成绩方面，女生（87.86）大于男生（84.10）；成绩标准差方面，女生（6.096）小于男生（7.033），见表7。

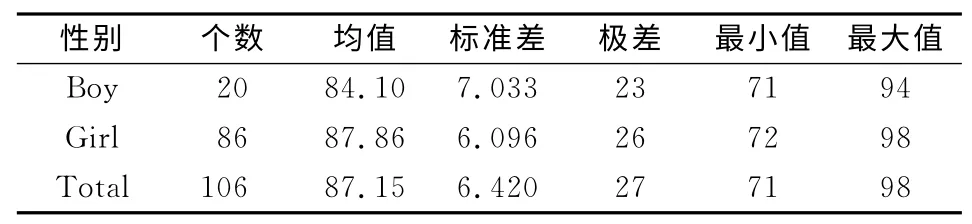
表7 成绩的基本描述性统计指标

三、讨论与结论

（一）关于试卷质量

根据数理统计学基本原理，一般考试成绩的分布应该符合正态分布，偏度介于0 与±3 之间［2］。经正态性检验，5个班级中仅A 班的成绩不符合正态分布，各班成绩的偏度、峰度均接近于0。因此成绩呈正态分布仅具有一般意义，并非绝对。

标准差是测定离散度的重要指标，若以标准差介于9～15之间判断试题质量为较好［2］，则该套试卷在D 班的表现为质量较好。这表明同一套试卷在不同情况下的表现可能不同，即标准差并非判断试题质量的唯一指标。

难度指测验试题的难易程度，一道试题的难度既可反映试题本身的复杂程度，又可间接反映教学状况。同一试题，在不同对象、不同环境中使用，所得的难度值不一定相同［1］。因此，命题时试题难度的掌握非常复杂［11］。

根据考试的目的和性质，一般期末考试难度值应低一些，而选拔考试难度应高一些［11］。但具体到试题难易程度的划分，仍存在不同的难度标准。如马少仙［5］认为，试卷难度P 在0.3～0.5之间为宜，P ＞0.7 为难题，P ＜0.2 为易题。任汉斌和单蓉［11］认为，期末考试难度值P 应介于0.2～0.4之间，小于0.2为易题。赵立新等［1］认为在常模考试中，大多数试题的难度值P 应控制在0.3～0.7之间，期末考试的试卷难度值P 控制在0.2～0.3之间较好，因为这样既有利于测量学生的真实水平，又能较好的控制不及格率。

但是，不及格率是一个敏感的话题。考虑到多方面的实际状况和实践经验，高年级专业课程考试的难度值P 实际上应控制在0.1～0.3之间为宜。这样既能让那些专业知识熟练的学生获得高分，又能让那些专业知识薄弱的学生勉强通过课程考试。

效度反映测量结果的准确性和有效性的程度［18］。效度的估计方法有3 大类，即内容效度、结构效度和效标关联效度［19］。但前两者无简单有效的定量统计方法，效标关联效度又称为统计效度或经验效度，可用测验分数和效标之间的相关系数来定量表示效度的高低［1］。

效标可分为外部效标和内部效标2类。效标不同，其效度可能大相径庭［1］。一般可选择公认的比较客观的一次考试成绩或前承（或后续）课程中相关课程的成绩作为外部效标［1］。但由于试题的外部效标难以寻找，因此可把试题总分作为内部效标，把试题得分与总分之间的相关系数作为该试题的效度［11］。通常认为效标关联效度E ＞0.7为优秀，介于0.4～0.7为较好，E ＜0.4为差［1，11］。

效度计算也可采用试题之间的相关系数来表示［7］。相关系数矩阵中各元素值越小，说明试卷覆盖面越宽；反之说明题目内容高度相关，应加以调整。一般要求相关系数小于0.2为好。

根据区分度的含义，试卷的区分度越大越好，这也比较难以做到［1］。另外，根据不同性质、目的和要求，可适当调整试卷区分度的评价标准［1，11］。一般认为区分度大于0.4为优，介于0.3～0.39为良好，介于0.2～0.29为尚可，小于0.2为差［1，5，11］。由于以总分为内部效标的效标关联效度计算结果表示了该题得分与总分具有的内在一致性，亦体现了被试者水平高低的鉴别能力，因此，试题的效度也是试题的一种区分度［11］。

信度指测量结果的稳定性或可靠性的程度，亦即测量的结果是否真实、客观地反映了考生的实际水平［9］。它是衡量考试质量的一个重要技术指标，其主要作用是判断考试的优劣［11］。在实际测量中，可用稳定性系数、等值系数、内部一致性系数、系数等来度量信度，而可操作性强的有分半信度和系数［1］。利用SPSS 等统计软件可以方便地求解系数，因此笔者建议采用该系数为信度指标，目的是统一计算方法和评价标准。

信度要求没有明确的标准，因考试性质和目的不同而异［1，11］。一般情况下，要求标准化测试的信度值在0.90以上［11］。对于期末考试，信度值大于0.9为优秀，介于0.7～0.9为较好，小于0.7为不合格试卷［1，11］。

由于没有更好的校标可供选择，为了统一计算方法和评价标准，笔者建议采用题目之间的相关系数作为效度指标，题目与总分之间的相关系数作为区分度指标。

传统试卷质量评价侧重对试卷进行宏观整体的分析与评价，或者注重成绩的基本描述性统计指标，或者注重试卷的4度指标。本研究表明，结合基本描述性统计指标的4度分析能更全面客观地反映考试结果。为了科学合理评价试卷质量，评价过程应避免单独使用某一种或某一类指标。一份具有合理的难度（介于0.1～0.3 之间）、较高信度（不小于0.9）、效度（题目间相关系数不大于0.2）和区分度（题目与总分间相关系数不小于0.4）、成绩近似正态分布的专业课试卷，应视为优秀试卷。这样，一方面可以为本科教学水平评估中的试卷质量分析提供依据，另一方面可以更科学、准确、有效地反映教师的授课水平和学生的学习效果［8］。

（二）关于学生成绩

本次取样的学生成绩在性别间有显著差异（Sig.=0.022＜0.05），班级间没有显著性差异（Sig.=0.359＞0.05）。

分析表明，作为教学对象的大学生具有显著的个体差异性［20］和一定的群体差异性。女生与男生学习成绩表现出来的显著性差异实际上反映了女生与男生在学习态度、学习能力、学习方法等方面的群体差异性。一般认为女生对英语的学习兴趣更强，时间投入更多。笔者对学生进行的面对面访谈也证实，女生对双语教学的兴趣普遍高于男生。

分析表明，班级之间没有显著性差异的原因可能有两种，一是课程性质为选修课，这至少保证绝大多数学生都有相似的兴趣基础，避免了必修课程的学生群体中可能存在的差异性；二是班风学风相近，这除了学生自身的原因，也与班级管理者有一定关系。

兴趣不足和时间投入较少都是造成学生学习压力的重要原因，而学习压力是造成大学生心理压力的重要影响因素之一［21］。大学教学是以大学生的发展为中心，以大学生的自由、全面、和谐发展为目标的创造性活动［20］。因此，在大学教学尤其是双语教学过程中，应在关注学生个体差异的基础上，关注学生的群体差异，搞好双语教学工作、提高双语教学质量。这是贯彻落实《教育部关于进一步深化本科教学改革全面提高教学质量的若干意见》精神、适应经济全球化和科技革命挑战、深化本科教育教学改革、推动高质量国际化人才培养的重要举措。

［1］赵立新，陈文艺，郭子君.试卷质量的定量评价［J］.华南农业大学学报：社会科学版，2004（4）：136-141.

［2］安萍莉，郭淑媛，王啬，等.大学考试试题质量研究［J］.高等农业教育，2006（2）：43-46.

［3］任艳玲，朱明放.基于统计软件SPSS 的学生试卷分析方法［J］.重庆工学院学报：自然科学版，2007，21（4）：95-98.

［4］徐全元，鲁莹，张雁.基于SPSS的“大学计算机基础”考试试卷分析［J］.电脑知识与技术，2009，36（5）：10484-10485，10497.

［5］马少仙.试卷质量的统计分析方法［J］.西北民族学院学报：自然科学版，2001，22（4）：13-16.

［6］冯子华，程立生，郑中兵.课程考核试卷质量分析的EXCEL实现［J］.高等农业教育，2004（3）：53-55.

［7］黄敏.数理统计在试卷分析中的应用［J］.玉溪师范学院学报，2004，20（3）：10-13.

［8］吴承祯，何丽华，林立群，等.试卷质量分析方法及其应用［J］.中国林业教育，2008，26（3）：26-30.

［9］曹雯梅，陈世昌，程亚樵，等.同异联系势综合分析法在高校试卷质量评判上的应用［J］.河南农业：教育版，2008（6）：3-4，6.

［10］刘淼.用数理统计的原理评估试卷质量［J］.大学数学，2009，25（2）：164-168.

［11］任汉斌，单蓉.基于MATLAB 的试卷质量分析方法研究［J］.广西民族师范学院学报，2011，28（3）：30-32.

［12］吴成秋，贺栋梁，黄波，等.SPSS for Windows在试卷分析中的应用探讨［J］.西北医学教育，2006，14（4）：401-403.

［13］张瑶，陈高云，王鹏.数据挖掘技术在试卷分析中的应用［J］.西南民族大学学报：自然科学版，2008，34（4）：839-842.

［14］谭庆.关联规则Apriori算法在试卷成绩分析中的应用研究［J］.信阳师范学院学报：自然科学版，2009，22（2）：300-303.

［15］谭庆.基于k-means聚类算法的试卷成绩分析研究［J］.河南大学学报：自然科学版，2009，39（4）：412-415.

［16］张晓翊，孟德欣，余翠兰.基于K-means算法的学生试卷成绩分析［J］.宁波大学学报：理工版，2010，23（4）：67-70.

［17］王孝玲.教育统计学［M］.2 版.上海：华东师范大学出版社，2001：156-193，311-336.

［18］胡中锋，李方.教育测量与评价［M］.广州：广东高等教育出版社，2000：31-58.

［19］美国教育研究会，美国心理学协会，全美教育测量学会.教育与心理测试标准［M］.燕娓琴，谢小庆，译.沈阳：沈阳出版社，2003：1-25.

［20］王本洋，罗富和.以人为本与因材施教的探讨［J］.中国林业教育，2010，28（1）：1-4.

［21］王本洋.农林类大学生心理健康状况SAD 分析［J］.中国林业教育，2009，27（2）：49-51.