竖向直排冻结条件水平冻胀力试验研究

李 岩 ，刘 波，张建新

（1.天津城建大学 天津市软土特性与工程环境重点实验室，天津 300384；2.中国矿业大学（北京）力学与建筑工程学院，北京 100083）

1 引 言

人工冻结工程中的土体冻胀现象影响范围广、持续时间长，是目前人工冻土理论研究和工程实践中的重要问题之一。具体表现为土体冻结后体积发生膨胀，使周边地层受到挤压和抬升。研究表明，冻结法施工过程中冻土内部发生的剧烈相变会造成相当大的冻胀力和变形，可能会对冻结工程周边地层环境造成严重影响，导致地下建筑、隧道、管线、基础工程和地表建、构筑物稳定性降低甚至发生破坏性变形。近年来，国内外通过模型试验对冻胀力的研究取得了很多进展。Jessberger 等[1]和陈湘生等[2]分别利用离心试验机，对深井冻结凿井工程和公路隧道联络通道冻结工程进行了离心模拟试验，模拟了人工冻结条件下不同类型土体的冻胀现象。李萍等[3]进行了开放系统下的饱和土体单向冻结试验，利用试验数据进行反演分析，总结出冻胀现象随冻土温度梯度变化的规律。Thimus 等[4]设计研制了试验装置，可以量测单冻结管在均质砂土或非均质黏土中形成冻结壁在不同起始温度下冻结过程中的轴向和侧向变形。王建平等[5]自行研制了人工冻土冻胀融沉模型试验装置，可以模拟开放补水和密闭隔水情况下的人工冻土一维和三维条件下冻结壁形成和融化的全过程。姚直书等[6]针对润扬长江公路大桥锚碇基坑支护工程，进行了深基坑冻土墙模型冻胀力试验研究，建立了大尺度排桩冻土墙模型，通过对比有、无卸压装置的情况下冻胀力测量值的对比，给出了卸载过程中冻胀力的变化趋势。汪仁和等[7]研制了冻土冻胀试验机，模拟了冻结土体侧向冻胀的性质，并总结了多圈环形人工冻结壁温度场和应力场的发展过程和相互影响。于琳琳等[8]针对粉质黏土进行了侧向人工冻结试验，得到了外部温度对冻土温度场和冻胀量的影响规律。东兆星等[9]从解析法计算和数值模拟方面总结了直排型冻土墙的受力特性和冻结壁厚度的确定方法。综上所述，国内外所进行的冻胀模型试验主要针对冻结管环形布置的情况，但对于软弱地层进行斜井井巷掘进和深基坑冻结法止水帷幕施工中经常采用的竖向直排冻结管布置，目前的冻胀研究资料和试验还比较欠缺。本研究针对竖向直排冻结过程中的水平冻胀力分布和变化特征进行了三维模型冻结试验，可供对应条件下冻结工程的稳定性提供参考。

2 试验方案和相似准则的确定

2.1 试验装置

试验在地下工程三维加载冻结模拟试验系统上进行，该系统由中国矿业大学（北京）自行研制，可进行多种情况下地下工程的冻结施工模拟，测试地层冻胀变形、冻结压力时空变异特性，温度场的分布与冷源冷量及冷冻时间之间的关系，未冻土体-冻结壁-井壁相互作用，挖掘与井壁砌筑作用下冻结壁及井壁的受力变形等，系统基本结构见图1。模型试验的主要内容包括测量竖向直排冻结过程中温度场的变化规律、低温冻结环境下土体所受的水平作用力等，分析冻结施工中温度场和冻胀力之间的相互影响，为研究探求竖向多直排冻结过程中冻结锋面移动对水平方向土体冻胀力的影响提供必要的试验数据。

图1 三维冻结试验系统结构简图Fig.1 The simple drawing of 3 dimensional freezing experiment system

2.2 试验背景和实施方案

试验以辽宁双树子斜井竖向直排冻结工程为原型设计。倾斜井筒冻结段主要位于第四系沉积土层内，自上到下分别为粉质黏土、粉质砂土、细砂，粗砂和砂砾等。需穿越的主要含水层为第四系砂及砂砾承压含水层，其中上部孔隙承压含水层为冻结控制层，含水率大，土质较软弱，如果冻结壁强度不够，极易发生地下水、流砂涌入掘进工作面的危险，使冻结失效，造成人员和财产重大损失。

均衡考虑相似模拟的实用性和可操作性，试验尽可能与冻结工程原型接近，并适当简化。由于所需岩土材料量大，无法使用现场的材料，故试验选用与现场相近的砂质粉土，选取最不利位置——孔隙承压饱和含水层的土体作为试验冻结段土体，并控制土体含水率与现场情况接近。冻结盐水温度为-30℃，冻结段土质为砂质粉土，通过对土体物理性质进行测试试验，获得土体物理力学和热学参数，见表1、2。

表1 土层主要物理力学参数Table 1 Soil physico-mechanical parameters

表2 土体热力学性质参数表Table 2 Soil thermodynamic parameters

土体的冻结温度为-0.2 ℃，原始地温为11 ℃。整个冻结段斜长为100.29 m，冻结深度为4.91～34.1 m，水平冻结长度为95.68 m。冻结段布置4 排冻结管，排间距为2.4 m，每排管孔间距为2.1 m，冻结孔孔径为0.18 m。冻结壁设计厚度井帮为1.8 m、底板和顶板为3.0 m，设定控制层冻结壁的平均温度为-6 ℃。

为充分验证各因素对试验的影响，保证试验的科学性和准确性，通过改变施加在模型试验台上的竖向荷载和积极冻结时间，进行了6 组相似模拟试验，对不同积极冻结时间的情况下各深度土体的温度和受力情况进行分析。

2.3 相似准则和试验缩比的确定

要顺利完成或达到上述试验目的，必须满足一定的相似准则，如温度场相似、水分场相似、应力场相似等。实际的试验过程中，由于设备所限，无法进行全长冻结试验，故根据相似理论，选取穿过代表性土层环境的斜井进行局部模拟冻结试验。结合冻结过程温度场、水分场和应力场的数学模型[10]，列出以下相似准则。

（1）温度场准则

首先根据瞬态导热基本公式，列出适合竖向直排冻结传热的导热方程：

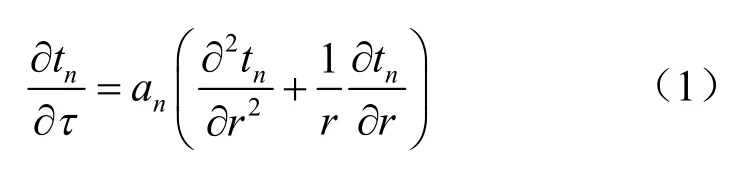
当τ＞0，0＜r ＜∞，在冻结锋面上有热量平衡方程：

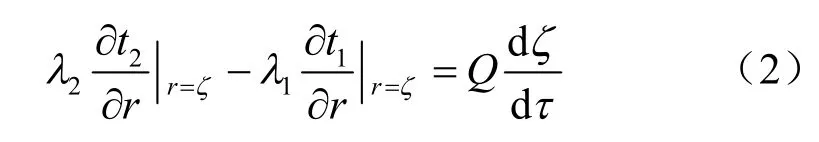
模型的初始条件和边界条件：

式中：r为已形成冻土柱内部各点到冻结管中心的距离；tn为r 位置的温度，n=1 表示未冻土，n=2表示已冻土；τ为冻结时间；an为导温系数；λ1、λ2分别为未冻土和冻土的导热系数；ζ为冻结壁边界位置坐标，即冻土柱扩展半径；Q为土体单元冻结过程中释放潜热量；tθ为周围土体的初始温度；t0为冻结管内盐水温度，即冷源温度，假设为恒定值；td为土体冻结温度。

根据式（1）、（2），冻结模型试验中温度场模拟包含的物理和热力学参数应为温度t、时间τ、土体比热容C、土体导热系数 λn、土体单元冻结所释放潜热量ψ、冷源温度 tc、冻结管外壁温度 tb、土体初始温度 t0。根据矩阵因次表法进行分析，得到了温度场的相似准则：

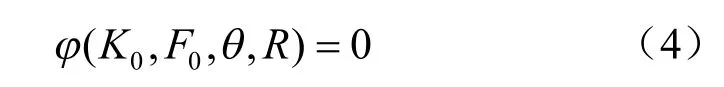
式中：K0为柯索维奇准则，为土体潜热，C为土体比热容，t为温度；F0为傅里叶准则，为土体导热系数；r为冻结锋面到冻结管的距离；θ为温度准则；R为几何准则。本试验所用土体与现场一致，故土体比热相似指标 Cc和导温系数相似指标 Ca均为1，并确定Cτ=。试验需要保证冻结壁几何尺寸l、冷源温度 tc、土体初始温度 t0和冻结时间τ与原型相似，即可实现温度场的模拟。

（2）水分场准则

基于正冻土水流迁移规律和渗流方程[11]，水分场方程为

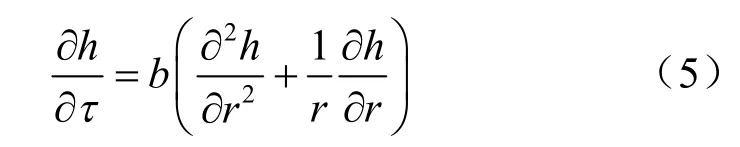
初始条件：

边界条件：

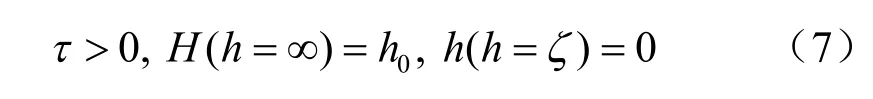
式中：h为土体单元的含水率；b为土体的导湿系数。

因此，确定水分场相似准则为

式中：Θ为湿度准则。在试验箱体内2 个相邻侧壁上布置有3 层不同高度的水管，各层水管分别由一个独立阀门控制，另外两侧的侧壁布置带有过滤布的可调排水孔。试验时，根据地下水的不同水位、不透水层位置来开关相应阀门和调整进水/排水量，通过土中模型上/下侧及周边以及进/排水孔附近位置埋置水分传感器，可以测量冻结过程中外围土体的含水率并进行调节，模拟真实情况的周边地下水环境。因此，在冻结壁几何尺寸相似的前提下，水分场可实现相似的“自模拟”。

（3）应力场准则

在人工冻结过程中，未冻土体和冻结壁所受的不同方向、不同性质的作用力情况相当复杂，为减少模型试验所需参数和具体实施步骤，因此，在尽量减少改变实际应力场的前提下对模拟应力场进行适当地合理简化，使之可以通过三维模型试验台进行模拟加载，简化后的应力、应变微分方程和侧向土压力方程分别为

式中：E为未冻土体的弹性模量；εr、εθ分别为土体的法向应变和切向应变；u为法向变形位移；μ为土体的泊松比；ρ为土体的密度；H为测量所处位置土体的深度，即巷道埋深；A为土体的侧压力系数。

根据推导出的应力-应变准则 E/ε、P/ρ h和几何关系准则 εr、εθ和u/r，对浅埋土体（H ＜150 m）的外部和自重荷载，土的自重应力和侧压力，通过使用与实际工程相近的相似模拟材料，并控制三维模拟系统施加与实际深度大小和方向相近的荷载，就能够为模型试验提供与现场情况近似一致的地应力环境。

对于冻结壁受力问题，可使模型试验中的冻结壁与工程现场冻结壁的傅里叶准则数相同，即两者的温度场分布和导热的不稳定程度近似相同。当试验的初始条件和边界条件能够相似，就可以使模型的冻结壁整体受力状态与现场实际的冻结壁所受整体应力状况相似[14]。

人工冻土冻结壁的强度σ 是有关温度、加载时间和载荷性质的函数，其中，温度t 是主要影响因素。本文假设模型与工程现场土体性质相同，只考虑冷源温度 tc、土体初始温度 t0和冻结时间τ 等因素，保证模型中上述因素与现场情况相似，实现了冻结壁受力相似模拟模型与工程原型的“自模拟”。

根据三维模型试验台和冻结管的管径，考虑到选择的几何缩比过大会产生明显的端部尺寸效应，影响试验的精度，据以往经验将几何缩比确定为1:15，从而确定时间缩比为1:225，土体弹性模量缩比、应力缩比、温度缩比均为1:1。

2.4 冻结过程施加外荷载的确定

埋深对模型的影响主要包括土体的自重应力和侧向土压力，如果试验需要模拟的巷道埋深为H，土压力P=γH，则相似模型所受到的上部土压力P′应与P 相等。上部土压力由模型试验台中测点上部覆土的自重和模型试验台加载系统竖向加载共同提供。本试验对2 段冻结段进行模拟，其上覆土的厚度分别为14.913 m和21.402 m，按照工程经验取平均重度为18 kN/m3，则实际位置上覆土自重应力为：上段268.434 kPa，下段385.236 kPa，近似对应力取整。试验时监测点上方上覆土层厚度为1.0 m，模型土重度为18 kN/m3，所以模型上覆土自重力为18 kPa。加载系统需提供的垂直压力为上段250 kPa，下段367 kPa，换算成面荷载为上段1 000 kN，下段1 468 kN。竖向荷载由系统上部反力架安置的液压千斤顶提供，底部用钢板与模型土体接触，以模拟均布面荷载。见图2。

图2 竖向加载装置Fig.2 Vertical loading system

2.5 冻结管和监测点的布置

根据原型情况和相似准则确定的试验缩比，模型试验台内布置了5 排4 列共20 根冻结管。冻结管直径为12 mm，排间距为180 mm，排内管间距为140 mm。考虑到冻结管布置具有对称性，且不能忽略相邻排冻结管之间的相互影响，沿主面和轴面方向分别均匀设置10 个和8 个监测点，另外，在井壁位置和冻结管右侧位置沿轴面方向分别设置5个监测点，见图3。

3 试验过程与结果分析

3.1 试验具体实施过程

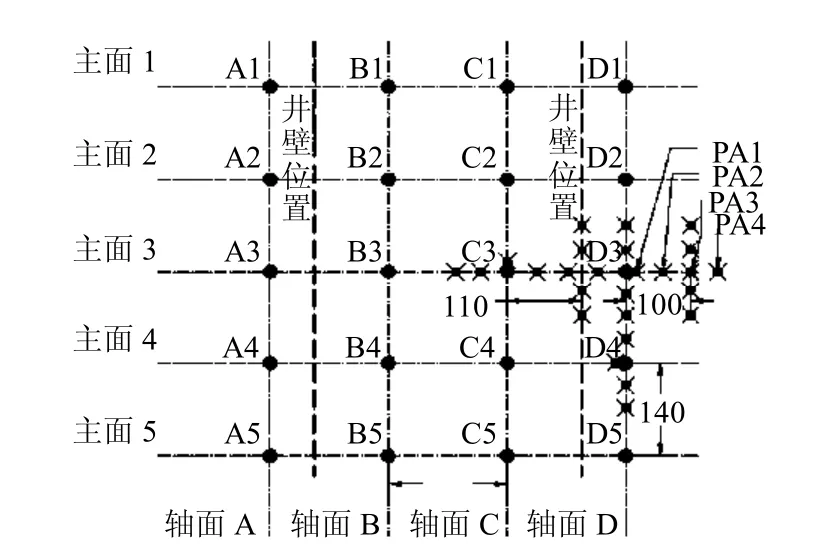
图3 冻结管和监测点的布置(单位:mm)Fig.3 Layout of freezing pipes and measuring points(unit:mm)

向模型试验台内分层逐步填充土体，在预设监测点布置热敏电阻和土压力盒，待土体静止充分固结后，从试验台不同区域取土进行土力学物理试验，获得土样的含水率、密度、孔隙比、黏聚力等物理力学参数，与现场土体保持一致，之后进行土体冻结。试验开始时，实验室环境温度约为14 ℃，冻结8 h 后橡胶软管周围和冻结管表面出现白霜，冻结管周围土体有干燥的迹象，见图4(a)。原因是已冻土体内自由水逐渐冻结成冰而使未冻水含量降低，随着冻结锋面的扩张，冻结锋面附近未冻土内水分会向冻结锋面移动并凝固，使干燥土体的范围不断增大。冻结16 h 之后，冻结管布置范围附近的表面土体全部干燥，并连接成为一体，见图4(b)。模型试验台表面土体干燥区域与未干燥区域分界线逐渐拉直变为近似直线。

图4 冻结过程的不同阶段Fig.4 Different stages of freezing process

冻结前期和停机之初，土体温度变化较快，数据采集频率设定为15 min 或30 min，而在土体的维护冻结阶段，温度变化相对缓慢，数据采集频率设定为60 min。

3.2 温度场分布规律

沿主面和轴面方向的各监测点温度分布规律分别如图5 所示。竖直方向上温度差异很小，同一水平面上距离冻结管越近，温度变化越快。

冻结管附近区域温度随时间的整体变化规律比较一致，而距离冻结管较远时温度随时间变化的规律较为不明显。外排冻结管附近温度明显高于与冻结管等距离的内部监测数据。

在该冻结管布置方式的情况下，轴面位置温度分布相对平均，温度变化受到位置影响程度小于主面位置，冻结锋面对轴面位置温度的影响差异较小，见图5(b)。因此，在对竖向直排冻结壁的温度场分布进行理论研究时，可假设冻结壁交圈成排后，冻结壁内部温度分布按平板冷源情况进行考虑。

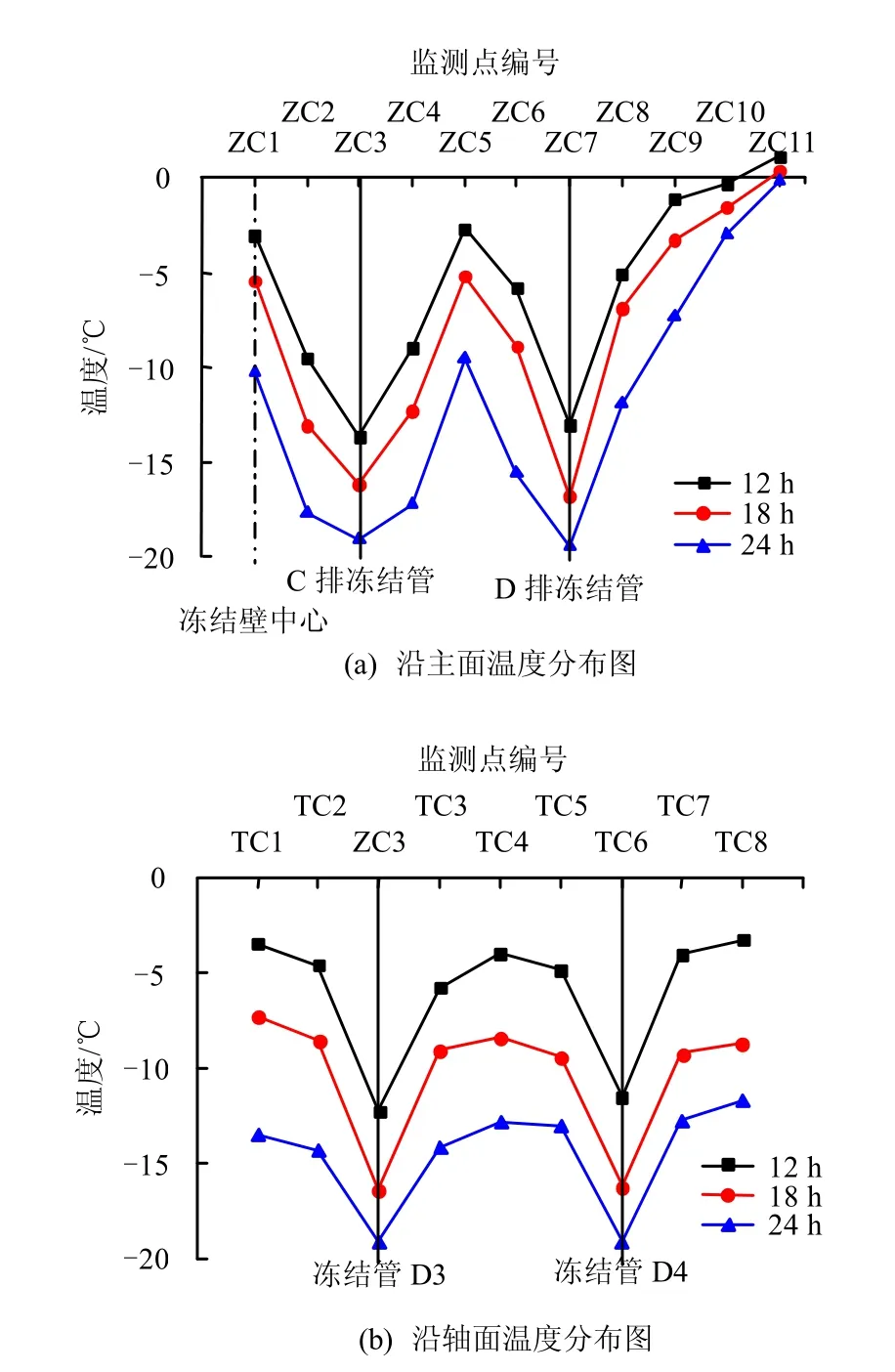
图5 冻结过程面温度分布Fig.5 Temperature distribution along different planes

冻结壁外侧距主面较远位置土体的温度值较高，且发展速度较慢，在实际冻结工程的过程中，对于该区域的冻结区域，应采取加强冻结的措施（如适当加密外侧冻结管），加强温度和压力的监测，防止因温度过高导致冻结失效。

3.3 水平冻胀力分布规律

试验主要研究冻结过程土体中水平冻胀力随冻结时间和冻结锋面位置的发展变化情况。冻结过程中，土体内部的受力情况非常复杂，难以直接测量冻结过程中土体所受到的冻胀力，本文假设冻结过程中土体应力变化的原因完全归结于冻胀作用，故通过测量冻结前土体内部的初始应力值和冻结过程中土体应力值之间的差值获得冻结过程中所受水平冻胀力的数值。此外，对于土体融化过程的冻胀力情况，针对其作用机制的研究还比较少，本研究仅分析冻结过程中水平冻胀力的发展和分布规律。

沿轴面方向水平冻胀力监测数据表明，冻结壁交圈后外部土体各位置的水平冻胀力大小基本相同，因此选取主面位置冻结壁外侧监测点PA1～PA4 对冻结管布置区域外侧土体的冻胀力进行分析，4 点按编号1～4 远离冻结管，测量数据如图6所示。

图6 冻结管外侧水平冻胀力变化曲线(积极冻结时间36 h)Fig.6 Test curves of horizontal frost heaving force outside of freezing pipes(active freezing time 36 h)

在上述试验研究的基础上，本文对土体水平冻胀力和冻结壁温度的关系进行了探讨。图7为冻结管外侧冻结壁水平冻胀力与温度拟合曲线。降温过程中水平冻胀力随温度近似呈二次抛物线关系，表达式为

式中：p、t 分别为水平冻胀力和温度。不同条件下（如外荷载、土体性质等）系数a、b、c 的取值不同，试验所得拟合系数和相关性系数见表3。

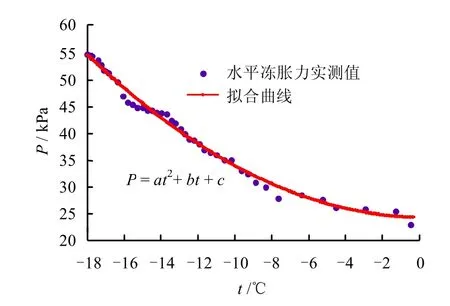
图7 外侧冻结壁主面位置水平冻胀力与温度拟合曲线Fig.7 Fitting curve of horizontal frost heaving force and temperature on the main plane outside of frozen wall

表3 拟合函数的系数取值Table 3 Parameters in fitting function

图7 表明，（1）冻结管外侧土体水平冻胀力在冻结过程中先迅速增大，在温度最低时刻附近达到最大值，之后随温度升高而缓慢减小，这是由于冻结时间会影响水分迁移的持续时间，所以维持水分迁移进行的时间越长，冻胀力越大；（2）水平冻胀力与冻结锋面的位置存在一定对应关系：距离冻结锋面越近，冻胀力变化率越大；（3）距离冻结管较近的位置水平冻胀力的峰值和变化速率越大，且峰值出现的时刻更早，除冻结管临近区域外，其他位置的水平冻胀力达到峰值后缓慢减小，并逐渐趋于一致；（4）水平冻胀力受到上部荷载的影响，上部荷载越大，土体在冻结过程中所受到的水平冻胀力越大。

对不同上部荷载P 条件下的2 组试验数据进行比较表明，P=367 kPa 时，水平冻胀力最大值约为57 kPa；P=250 kPa 时，水平冻胀力的最大值约为42 kPa。

分析井壁位置的平均水平冻胀力监测数据表明，冻结壁交圈之前，水平冻胀力变化规律与外部土体相似，井壁位置水平冻胀力的最大值高于外部土体，P=367 kPa 时，井壁位置水平冻胀力最大值约为66 kPa；P=250 kPa 时，水平冻胀力的最大值约为47 kPa，但冻结壁排间交圈后水平冻胀力变化的规律性并不明显，如图8 所示。

将现场冻结管外侧冻结壁深度为21.4 m 的温度和水平冻胀力监测数据（对应上部荷载P=367 kPa）与拟合方程式（10）的计算结果进行比较，见表4。结果表明，拟合方程计算数据小于现场值，但相差均控制在15%以内，两者冻胀力随时间变化的规律性吻合较好。

图8 不同竖向荷载下斜井井壁平均水平冻胀力曲线Fig.8 Average horizontal frost heaving force curves of inclined shaft wall position in different vertical load

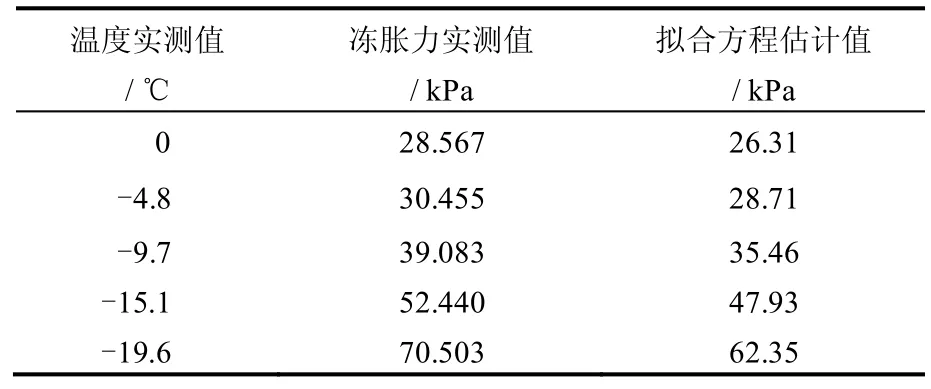
表4 水平冻胀力现场实测值与试验拟合方程计算值的比较Table 4 Comparison between measured values and fitting formula calculation values of horizontal frost heaving force

4 讨 论

模型试验中影响试验结果的影响因素较多，故试验结论还应通过理论和现场实践进一步验证，对结论产生的本质原因也需通过冻土三轴试验等方法继续深入研究。根据模型试验总结的水平冻胀力的分布和变化规律，进行如下讨论：

（1）研究表明，冻结锋面向未冻土体推进的速度直接决定正冻土冻胀力的大小[13-14]。这一点在试验中得到了充分验证，就冻胀力本身而言，其影响因素可分为内在和外部因素两种。内部因素主要包括土体本身物理力学性质，包括土的颗粒级配、含水率和土中水的冰点等。影响冻胀程度的外部因素主要包括土体所受外力、所处深度和冻结时间等。本文主要研究了温度因素对水平冻胀力的影响，其他因素对土体水平冻胀力的规律在今后的试验研究中进行探求。

（2）试验中发现，在冻结管外部区域，除冻结管临近位置外，其他位置的水平冻胀力达到峰值后缓慢减小，各位置冻胀力的值逐渐接近。笔者认为这种现象的出现可能是模型试验台侧壁产生的侧限作用的影响，冻土扩展使周边未冻土体不断被向外排挤，受到模型试验台侧壁的阻挡，各位置内部应力不断增加并密实，应力达到稳定并趋于一致。对于无侧限情况下水平冻胀力的变化情况，需要对试验进行改进以继续深入研究。

（3）冻结壁内部的水平冻胀力在达到最大值后，数值波动比较大，笔者认为，可能是由于排间冻结管之间存在相互影响，造成排间土体的温度梯度反复变化，致使水平冻胀力的大小和方向不断改变，影响了压力传感器的测量结果，至于多排冻结管影响下温度变化的内在机制和形式，仍需进一步研究和总结。

5 结 论

（1）冻结管外部水平冻胀力的最大值主要取决于沿主面方向到冻结管的距离，冻结壁交圈后沿轴面方向的水平冻胀力大小基本相同。降温过程外部冻结壁水平冻胀力与温度的关系可通过二次抛物线拟合，相关系数大于0.97。冻结管排间的水平冻胀力受到多排冻结管的影响，分布比较复杂，但最大值明显大于外部区域。冻胀力的变化率主要受冻结锋面位置的影响，距离冻结锋面较近时，冻胀力的变化率逐步达到峰值。

（2）对于同一种土体，上部荷载P 对水平冻胀力的影响明显，体现在不同埋深位置水平冻胀力的变化趋势上，其他条件相近情况下同一水平位置的深度越大，所受水平冻胀力越大。且井壁位置受力要大于外部土体。

结合特定斜井冻结工程，首次进行了竖向多直排冻结情况下的三维相似模型试验，获得了大量温度场和水平冻胀力的测量数据，为类似条件下矿井和城市隧道冻结工程的设计和施工提供了科学依据。

[1]JESSBERGER H L.Ground freezing 1988[C]//Proceedings of 5th International Symposium on Ground Freezing.Netherlands:BALKEMA A A,1989:407-411.

[2]陈湘生,濮家骝,罗小刚,等.土壤冻胀离心模拟试验[J].煤炭学报,1999,24(6):615-619.CHEN Xiang-sheng,PU Jia-liu,LUO Xiang-gang,et al.Centrifuge modeling tests of soil freezing heave[J].Journal of China Coal Society,1999,24(6):615-619.

[3]李萍,徐学祖,陈峰峰.冻结缘和冻胀模型的研究现状与进展[J].冰川冻土,2000,22(1):90-95.LI Ping,XU Xue-zu,CHNG Feng-feng.State and progress of research on the frozen fringe and frost heave prediction models[J].Journal of Glaciology and Geocryology,2000,22(1):90-95.

[4]THIMUS A.Ground freezing 2000[C]//Proceedings of the International Symposium on Ground Freezing and Frost Action in Soils.Netherlands:BALKEMA A A,2000:293-299.

[5]王建平,王文顺,史天生.人工冻结土体冻胀融沉的模型试验[J].中国矿业大学学报,1999,28(4):303-306.WANG Jian-ping,WANG Wen-shun,SHI Tian-sheng.Model experiment of frost heave and thawing settlement of artifically frozen soils[J].Journal of China University of Mining and Technology,1999,28(4):303-306.

[6]姚直书,程桦,夏红兵.特深基坑排桩冻土墙围护结构的冻胀力模型试验研究[J].岩石力学与工程学报,2007,26(2):415-420.YAO Zhi-shu,CHENG Hua,XIA Hong-bing.Model test study on frost-heaving force in retaining structure of row-piles and frozen soil wall of super deep foundation pit[J].Chinnese Journal of Rock Mechanics and Engineering,2007,26(2):415-420.

[7]汪仁和,李栋伟.多圈管冻结模型试验及水热耦合数学模型研究[J].合肥工业大学学报,2007,30(11):1481-1485.WANG Ren-he,LI Dong-wei.Study on model experiment with multi-freezing-tube cycles and the mathematic model of moisture-heat coupling in frozen soil[J].Journal of Hefei University of Technology,2007,30(11):1481-1485.

[8]于琳琳,徐学燕.人工侧向冻结条件下土的冻结试验[J].岩土力学,2009,30(1):231-235.YU Lin-lin,XU Xue-yan.Test analysis of disturbed soil by lateral artifical freezing[J].Rock and Soil Mechanics,2009,30(1):231-235.

[9]东兆星,崔广心.深基坑支护中冻土墙力学特性研究综述[J].岩土力学,2002,23(5):622-626.DONG Zhao-xing,CUI Guang-xin.Comment on research of mechanical characteristics of frozen soil walls in deep foundation pit support[J].Rock and Soil Mechanics,2002,23(5):622-626.

[10]崔广心.相似模拟与模型试验[M].徐州:中国矿业大学出版社,1990.

[11]汪仁和,李栋伟.人工多圈管冻结水热耦合数值模拟研究[J].岩石力学与工程学报,2007,26(2):355-359.WANG Ren-he,LI Dong-wei.Research on hydrothermal coupling numerical simulation with artificial multi-freezing-tube cycles[J].Chinnese Journal of Rock Mechanics and Engineering,2007,26(2):355-359.

[12]乔京生,陶龙光.地铁隧道水平局部冻结施工应力与位移场数值模拟分析[J].铁道建筑,2004,44(2):39-41.QIAO Jing-sheng,TAO Long-guang.Stress and displacement field analysis of partial horizontal freezing in subway tunnel construction[J].Railway Engineering,2004,44(2):39-41.

[13]孙家学,刘斌.冻结壁原始冻胀力的分析与计算方法[J].东北大学学报,1995,16(3):243-247.SUN Jia-xue,LIU Bin.Analysis and calculating method of using primary heave pressure to freeze shaft wall[J].Journal of Northeastern University,1995,16(3):243-247.

[14]吴礼舟,许强,黄润秋.非饱和黏土的冻胀融沉过程分析[J].岩土力学,2011,32(4):1025-1028.WU Li-zhou,XU Qiang,HUANG Run-qiu.Analysis of freezing-thawing test process of unsaturated clay[J].Rock and Soil Mechanics,2011,32(4):1025-1028.