三峡库区马家沟滑坡滑体粗粒土蠕变试验研究

胡新丽，孙淼军，唐辉明，谢 妮，郭 嘉

（中国地质大学（武汉）工程学院，武汉 430074）

1 引 言

由于滑坡岩土体的蠕变属性，大量滑坡在重力等内外地质营力的作用下呈现出长期而缓慢的变形特征[1-3]。此类滑坡不但在蠕滑阶段会对滑坡区的建筑和设施产生不利影响，亦有数量众多的蠕变滑坡在长期缓慢变形后演化为快速滑动滑坡，造成更为严重的经济损失。因此，系统地研究蠕变滑坡岩土体的蠕变特性对滑坡的演化阶段划分和长期安全性评价至关重要。

对于滑坡体物质蠕变性质研究主要是基于黏土、粉质黏土等相对均质材料的试验研究[3-7]，然而三峡库区滑坡体物质成分为含有大量碎石、砾石的非均质土体，国内外大量研究表明，大粒径物质对于土体的变形和强度性质有显著的影响[8-12]，在制样过程中人为剔除大粒径物质，势必影响土体蠕变特性。另一方面，当前国内外滑坡岩土体蠕变特性研究均针对滑带物质，而大量的滑坡深部位移监测表明滑体的缓慢变形不仅受滑带变形的控制，同时受到滑体物质变形特征的影响[13-15]。所以，针对滑体粗粒土开展大尺寸蠕变试验研究，对于了解滑坡体蠕变性质十分必要。

马家沟滑坡位于湖北省秭归县归州镇长江支流吒溪河左岸，为一典型的堆积层滑坡。为了研究该滑坡的演化特征和长期安全性，本次进行了滑坡体粗粒土在不同围压、不同应力水平下的多级加载三轴固结排水试验。根据滑坡长期变形过程中的排水条件，采用排水试验比不排水条件更符合实际情况。基于粗粒土蠕变试验成果，分析滑坡滑体土的蠕变特性，并采用Singh-Mitchell（S-M）蠕变模型拟合蠕变曲线，试验曲线和模型曲线的比较结果表明Singh-Mitchell 能较好地描述试验土体的蠕变行为。

2 试验材料和方法

2.1 试验设备及试样

试验设备为YLSZ150-3 型三轴蠕变试验仪（见图1），轴向加载设备经过改装后由原来的应变控制式转变为应力控制式。仪器的系统由竖向荷载加载、稳压、控制系统，周围压力加载、稳压、控制系统，三轴压力室，反力框架，位移、体变量测系统，荷载传感器及数据采集系统等组成。为了能提供蠕变试验需要的稳定轴压，仪器配有专门稳压的高压蓄能罐。

图1 应力控制式三轴蠕变仪Fig.1 YLSZ150-3 stress-controlled machine

试样尺寸（直径×高度）为φ 150 mm×300 mm。粗粒土试样取自马家沟滑坡试验桩开挖竖井中，取样深度在2.0～3.0 m 处。试样天然状态物理性指标见表1，颗粒级配见表2。

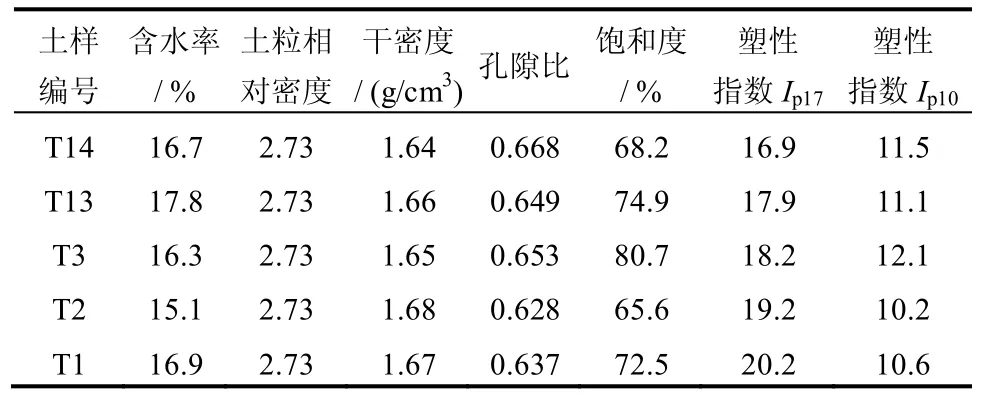
表1 试样物性指标Table 1 Physical properties of the specimen sets

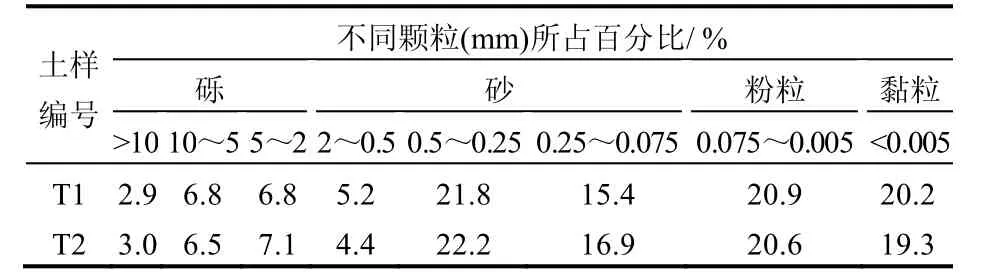
表2 滑体粗粒土级配Table 2 Grain size distribution of soils

2.2 试验方案

三轴蠕变试验主要分为2 步进行。第1 步，对土样进行常规三轴固结排水（CD）试验，根据滑坡滑体厚度，围压σ3等级确定为0.1、0.2、0.4、0.6 MPa，通过CD 试验得到不同围压下的破坏偏应力 qf。第2 步，根据常规三轴得到的破坏偏应力，按围压σ3的数值计算各级应力水平SL=0.1、0.2、0.4、0.6 下的偏应力竖向荷载，然后分别开展不同围压、不同偏应力水平下的三轴排水蠕变试验。

蠕变试验中对轴向和体积变形进行实时监测，根据大量的试验资料分析认为，一般体积变形要先于轴向变形达到稳定标准[16]，因此，蠕变试验中以轴向变形作为试验控制标准。本次蠕变试验中每级轴向荷载稳定时间10～18 d，记录不同时刻试样变形，当达到预定时间后施加下一级荷载。

为了避免温度变化对试验成果的影响，试验室温度控制在20 ℃左右。

3 试验结果与分析

3.1 粗粒土蠕变规律

由于采取分级加载方式，需要根据Boltzmann线性叠加原理推导各级荷载作用下的轴向应变-时间关系[17-18]，试验曲线如图2 所示。

由图2 可见，滑体粗粒土为典型的蠕变材料，在各级荷载作用下呈现衰减蠕变特征，粗粒土蠕变分为3 个阶段，即瞬时弹塑性变形、初始蠕变和稳态蠕变。施加一级荷载后，粗粒土产生瞬间变形，随后轴向变形随时间变化，初始阶段土体轴向变形随着时间增长蠕变速度不断减小，经过一定时间后轴向蠕变速度趋于稳定值，可见滑体粗粒土经历减速蠕变和等速蠕变阶段后，但试样并未出现加速蠕变阶段。

粗粒土蠕变量与偏应力绝对值呈正相关性，围压为0.6 MPa、应力水平为0.1、0.2、0.4、0.6 时，相应的蠕变量分别为0.70%、1.00%、1.13%、1.72%，应力水平同为0.4、围压为0.1、0.2、0.4、0.6 MPa时，相应蠕变量为0.31%、0.51%、0.76%、1.13%。

整理试验数据可以得到粗粒土经历减速蠕变过程的时长（即等速蠕变开始时间），见表3。由表可知，粗粒土经历减速蠕变时长随着应力水平的增加而增加，与偏应力的绝对值无关。

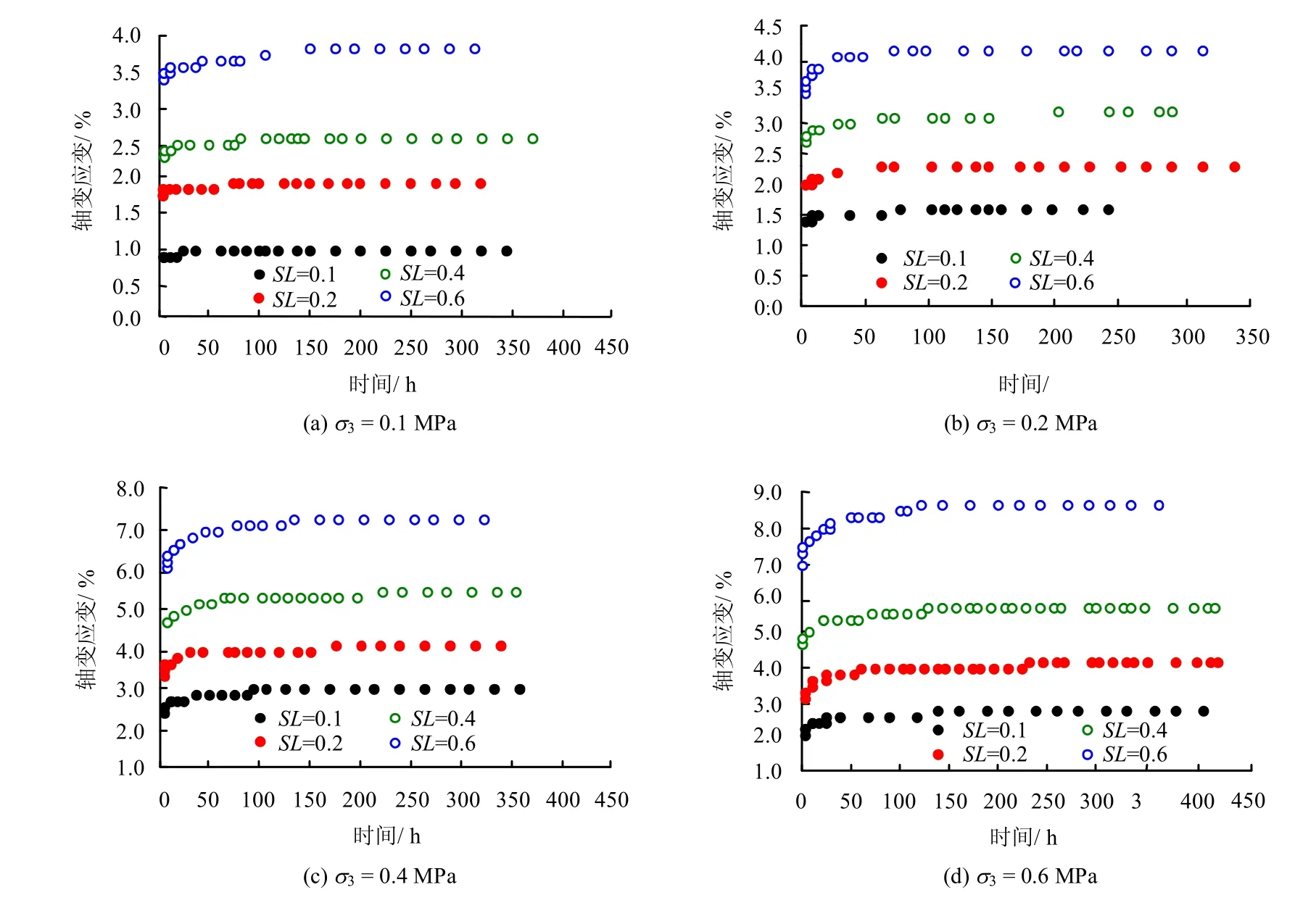
图2 不同围压下粗粒土轴向应变-时间关系曲线Fig.2 Axial strain-time relationship curves under different confining pressures

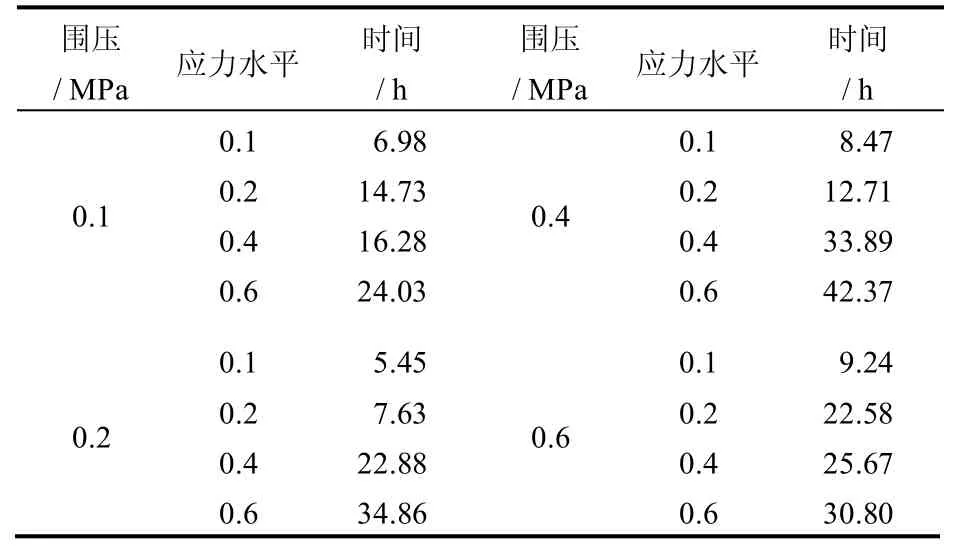
表3 试样等速蠕变开始时间统计结果Table 3 Starting time of the constant speed creep

土体蠕变主要由2 个因素引起，（1）颗粒的位置调整，即在荷载作用下土颗粒随时间不断发生旋转和移动；（2）颗粒在荷载的持续用下发生与时间相关的疲劳破裂，后者为土体在持续高应力作用下的蠕变机制，前者则在高、低应力值时均可对土体的蠕变性质产生影响[19-22]。本次试验的最高偏应力值为0.75 MPa，土体颗粒在此应力值下很难产生疲劳破裂[22]，因此，滑体粗粒土的蠕变机制与颗粒的旋转和相对移动相关。

加载试样时，土体颗粒在荷载作用下发生旋转和偏移，特别是接触配位数少的颗粒由于受力不均衡不断向土体孔隙填充，颗粒运动的结果是土体孔隙不断被填充，孔隙率持续减小，随着颗粒的接触配位数不断增大，发生位置调整的颗粒数减少，颗粒旋转和移动幅度亦较少，使颗粒蠕变的速度不断减小，当颗粒的配位数达到一定值时，颗粒间形成稳定的应力链，从而使变形的速率稳定或者不再发生继续变形[23-24]。当相同围压作用下增加偏应力水平时，土体颗粒形成稳定应力链的时间增加，即试验曲线中减速蠕变持续的时间增加。

3.2 粗粒土长期强度

长期强度是土体长期安全性的一个重要参数，与时间密切相关。通常可按照以下两种方法来确定土体蠕变的长期强度[4]：（1）某级偏应力作用下，轴向蠕变与时间的关系曲线上出现明显的稳态流变向加速流变转化的现象，该应力可视为长期强度。（2）当土体蠕变曲线未出现加速蠕变时，分别以轴向变形量和应力为轴作等时曲线，确定各等时曲线上的拐点，拐点所对应的偏应力即为长期强度。

由于本试验中滑坡粗粒土并未出现加速蠕变阶段，本文采用等时曲线法来确定长期强度值。等时曲线是指在一定围压下某个时刻不同应力水平下的应力-应变关系曲线。等时曲线可以通过以下方法绘制：在某一围压所用下，在不同应力水平下的蠕变曲线中选定一系列时刻t（如2、8、20 h 等），作时间坐标轴的垂线，与各蠕变曲线交汇得到一系列应力与应变值，将其绘制以应变和应力坐标轴的坐标系统中得到某时刻的等时曲线及得到不同时刻的等时曲线。图3为滑坡粗粒土的等时曲线。

图3 不同围压下等时曲线Fig.3 Isochronous stress-strain curves under different confining pressures

由图3 可知，曲线簇均具有双拐点的特征，第一个拐点在轴向应力增加到一定阶段时，由弹性阶段转向非线性黏弹性阶段的力学特征；第二个拐点试样由黏弹性变形向黏塑性变形转变。选取第二拐点作为粗粒土的长期强度值。曲线簇之间的间隔随着围压的增大而增大，也随着轴向应力的增加而增大，但其增加的幅度没有前者引起的显著。围压为100、200、400、600 kPa 时长期强度分别为108、158、265、390 kPa。

比较长期强度与瞬时强度可知，滑体粗粒土的长期抗剪强度均低于其瞬时抗剪强度。围压为100、200、400、600 kPa 所对应的长期抗剪强度相比瞬时抗剪强度分别降低48.6%、48.2%、49.0%、48.0%。结果显示，不同围压所用下粗粒土的长期抗剪强度约为瞬时抗剪强度的52%。

4 蠕变模型选择及其参数确定

4.1 Singh-Mitchell 模型

按照滞后变形理论，蠕变过程中的总应变可以分为瞬时产生的弹塑性应变和滞后产生的黏滞应变两部分：

式中：ε 总应变；εi为瞬时变形；εc为与时间相关的弹塑性变形。

一般来说，蠕变变形 εc与应力、时间有关，尽管其函数较为复杂，但可用应力和时间的复合函数表示[25]：

式中：f(σ)为应变-应力函数；g(t)为应变-时间函数。

应力-应变和应变时间关系均可选用不同的函数形式，其中应力-应变关系广泛使用的为指数函数和双曲线函数，应变-时间关系则较多地采用幂函数、对数函数和双曲线函数[25]。

S-M 模型[26]是基于大量的各种类型土体以及不同应力条件下的蠕变试验而得到的一种经验本构模型，至今广泛应用于描述诸多土类的蠕变行为。S-M 模型的应力-应变关系为指数函数，应变-时间关系则均采用的是幂函数。其模型方程为

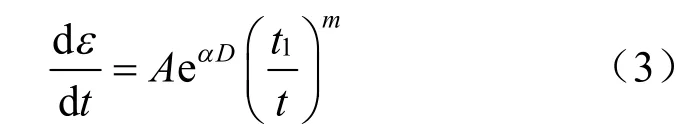
式中：ε为轴向应变；t为加载时间；D为偏应力水平，D=(σ1-σ3)/(σ1-σ3)f，(σ1-σ3)f可由三轴排水压缩试验获得；t1为单位参考时间；数学上为参数A 定义的时间，A为ln(dε/d t)-D 关系曲线中t=t1时的值；m为ln(dε/dt)-lnt 关系曲线中的斜率绝对值；α为应变速率对数与剪应力关系图中线性段的斜率。

对式（3）积分，可得

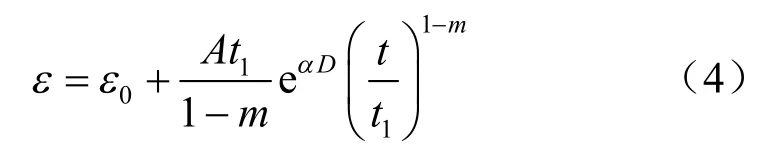
当 ε0=0 时，式（4）变换为式（5）。

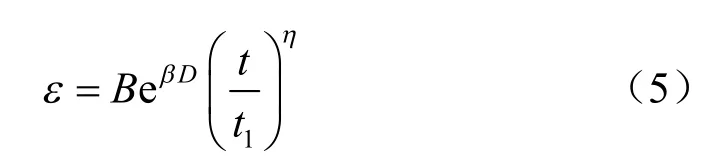
式中：B=At1/(1-m)，β=α，η=1-m。虽然假设式（4）中 ε0=0，但众多研究表明，式（5）足以适合描述诸多土类的蠕变行为。

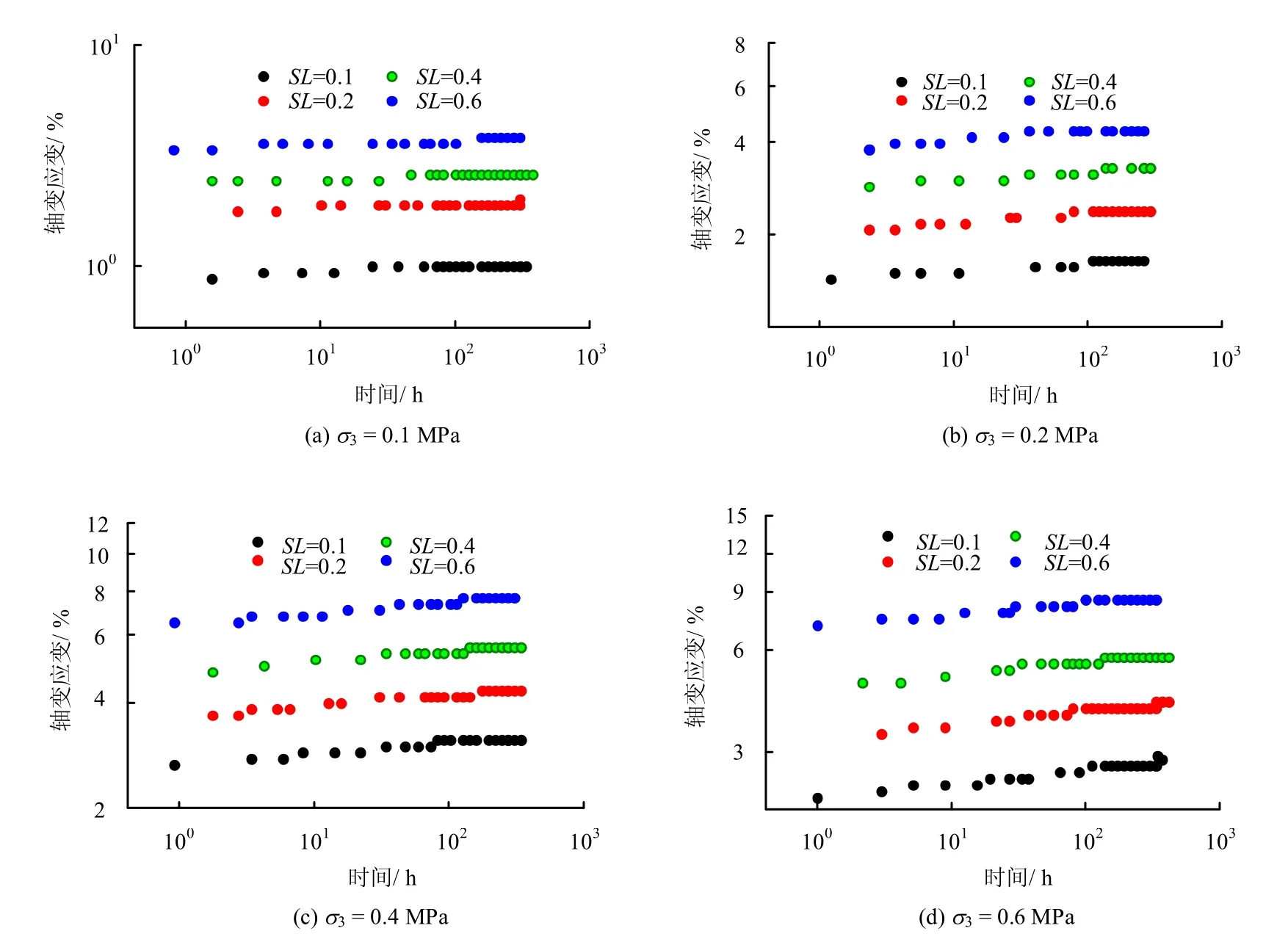
图4 双对数坐标下粗粒土轴向应变-时间关系曲线Fig.4 Axial strain-time relationship curves in log-log coordinate

当t=t1时，式（5）指数型应力-应变弹塑性模型形式为

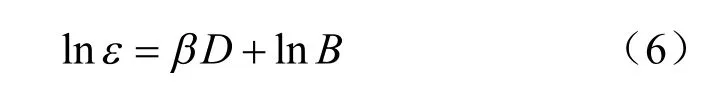
4.2 蠕变方程的建立

根据图3 绘制lnε 关于lnt 的关系曲线。从图4中可以看出，在相同围压、不同应力水平下的lnε-lnt 曲线为直线，且斜率即η 值近似相同，用S-M模型描述滑坡滑体粗粒土的蠕变特性是比较合适。本文η 值取每个围压下不同应力水平状态的一组拟合直线的斜率的平均值。

取单位参考时间 t1=1 h，得到相应的lnε与应力水平D 的关系曲线如图5 所示，结合式（5），可以确定出每个围压下的β、B 值。

滑体粗粒土的S-M 模型拟合参数见表4。将表中的参数代入式（5），可得4 个土样的S-M 蠕变方程式（7）。

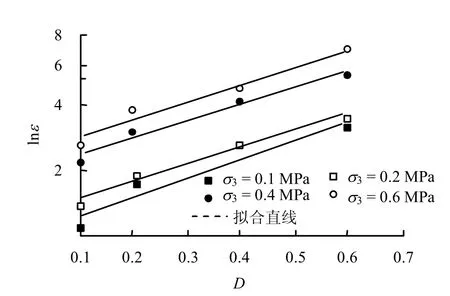
图5 lnε与应力水平关系图Fig.5 lnε-stress level relationship curves

表4 粗粒土的经验蠕变模型参数Table 4 Parameters of empirical creep model

4.3 模型验证

将章节4.2 建立的蠕变模型方程与试验曲线进行比较，结果如图6 所示。由图可见，试验与模型预测的应变趋势和量值基本一致，特别是加载200 h以后，S-M 模型预测的轴向应变基本与试验数据相同，以0.1 MPa 围压加载312 h为例，各级应力水平下模型预测误差分别为2.5%、0.6%、1.2%和2.1%。然而，加载早期S-M 模型计算值与试验值存在一定差别。偏应力水平较低时，S-M 模型计算值高于于试验 值，随着应力水平地提高，模型预测值则较试验值偏小。总的来说，S-M 模型基本上还是能够反映该滑体土的蠕变特性的。

考虑到研究对象为滑坡，其破坏前的蠕变时间长达几年甚至几十年，对于蠕变的长期预测显得更为重要，本文所采用的模型对于加载后期的预测更为精确，作为马家沟滑坡滑体粗粒土的蠕变模型是合理可行的。

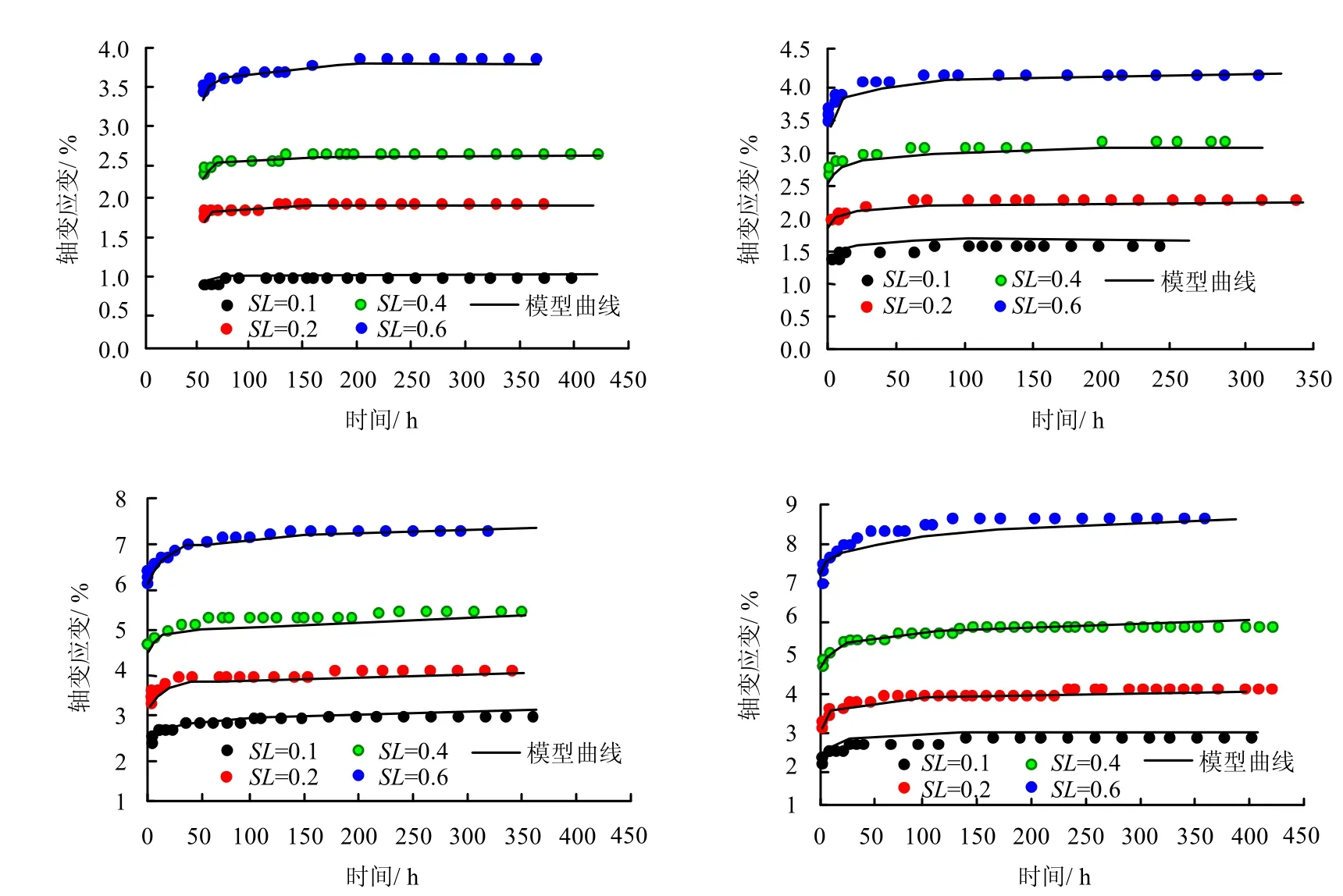
图6 试验数据与模型计算结果比较Fig.6 Comparison between test and calculated results

5 结 论

（1）滑体粗粒土呈现明显的衰减蠕变特征，蠕变阶段主要由减速蠕变和稳定蠕变2 个阶段，减速蠕变阶段的持续时间主要由应力水平的大小决定，最终的蠕变量值则受偏应力对值的影响，即围压和应力水平对粗粒土的最终蠕变量均可产生影响。

（2）土体等时曲线均具有双拐点的特征，分别表征由弹性阶段转向非线性黏弹性阶段和由黏弹性变形向黏塑性变形转变的力学特征，选取第二拐点作为粗粒土的长期强度值。比较长期强度与瞬时强度可知，滑体粗粒土的长期抗剪强度均低于其瞬时抗剪强度，且不同围压下长期抗剪强度约为瞬时抗剪强度的52%。

（3）采用应力-应变关系为指数函数，应变-时间关系采用幂函数的S-M 蠕变模型描述滑体粗粒土的蠕变行为。比较表明，该模型对加载后期轴向变形的预测效果较加载前期好，且模型能较为准确地反映蠕变的趋势和量级，考虑到滑坡蠕变的持久性，采用S-M 模型预测滑坡粗粒土蠕变变形是合理可行的。

本研究为三峡库区马家沟滑坡-防治结构体系的相互作用数值分析及确定滑坡-防治结构体系的长期安全性评价提供了充分的数据和合理的模型。

[1]Van DEN HAM G,ROHN J,MEIER T,et al.A method for modeling of a creeping slope with a visco-hypoplastic material law[J].Mathematical Geology,2006,38(6):711-719.

[2]BOZZANO F,MARTINO S,MONTAGNA A,et al.Back analysis of a rock landslide to infer rheological parameters[J].Engineering Geology,2012,131:45-56.

[3]王琛,胡德金,刘浩吾,等.三峡泄滩滑坡体滑动带土的蠕变试验研究[J].岩土力学,2003,24(6):1007-1010.WANG Chen,HU De-jin,LIU Hao-wu,et al.Creep tests of sliding zone soils of Xietan landslide in Three Gorges area[J].Rock and Soil Mechanics,2003,24(6):1007-1010.

[4]严绍军,项伟,唐辉明,等.大岩淌滑坡滑带土蠕变性质研究[J].岩土力学,2008,29(1):58-68.YAN Shao-jun,XIANG Wei,TANG Hui-ming,et al.Research on creep behavior of slip band soil of Dayantang landslide[J].Rock and Soil Mechanics,2008,29(1):58-68.

[5]赖小玲,叶为民,王世梅.滑坡滑带土非饱和蠕变特性试验研究[J].岩土工程学报,2012,32(2):286-293.LAI Xiao-ling,YE Wei-ming,WANG Shi-mei.Experimental study on unsaturated creep characteristics of landslide soils[J].Chinese Journal of Geotechnical Engineering,2012,32(2):286-293.

[6]王志俭,殷坤龙,简文星.万州区红层软弱夹层蠕变试验研究[J].岩土力学,2007,28(增刊):40-44.WANG Zhi-jian,YIN Kun-long,JIAN Wen-xing.Experimental research on creep of incompetent beds in Jurassic red clastic rocks in Wanzhou[J].Rock and Soil Mechanics,2007,28(Supp.):40-44.

[7]PETLEY D N,HIGUCHI T,PETLEY D J,et al.Development of progressive landslide failure in cohesive materials[J].Geology,2005,33(3):201-204.

[8]EL DINE B S,DUPLA J C,FRANK R,et al.Mechanical characterization of matrix coarse grained soils with a large-sized triaxial device[J].Canadian Geotechnical Journal,2010,47(4):425-438.

[9]HAM T G,NAKATA Y,ORENSE R P,et al.Influence of gravel on the compression characteristics of decomposed granite soil[J].Journal of Geotechnical and Geoenvironmental Engineering,2010,136(11):1574-1577.

[10]BAGHERZADEH-KHALKHALI A,MIRGHASEMI A A.Numerical and experimental direct shear tests for coarsegrained soils[J].Particuology,2009,7(1):83-91.

[11]ISHIKAWA T,MIURA S.Influence of freeze-thaw action on deformation-strength characteristics and particle crushability of volcanic coarse-grained soils[J].Soils and Foundatiaons,2011,51(5):785-799.

[12]VENKATARAMA REDDY B V,LATHA M S.Influence of soil grading on the characteristics of cement stabilised soil compacts[J].Materials and Structures,2014,doi:10.1617/s11527-013-0142-1,2014-06-27.

[13]简文星,杨金.三峡库区黄土坡滑坡I 号崩滑体成因[J].地球科学,2013,38(3):625-631.JIAN Wen-xing,YANG Jin.Formation mechanism of No.1 part slide of Huangtupo landslide in the Three Gorges Reservoir area[J].Earth Science,2013,38(3):625-631.

[14]李迪,张漫,李亦明,等.堆积体滑坡稳定性的实时定量评价法[J].岩石力学与工程学报,2008,27(10):2146-2152.LI Di,ZHANG Man,LI Yi-ming,et al.Real-time quantitative assessment method of stability for talus landslide[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2146-2152.

[15]汤罗圣.三峡库区堆积层滑坡稳定性与预测预报研究[D].武汉:中国地质大学.2013.

[16]于浩,李海芳,温彦锋,等.九甸峡堆石料三轴蠕变试验初探[J].岩土力学,2007,28(增刊):103-106.YU Hao,LI Hai-fang,WEN Yan-feng,et al.Study on triaxial creep test for Jiudianxia rockfill materials[J].Rock and Soil Mechanics,2007,28(Supp.):103-106.

[17]陈宗基,康文法,黄杰藩.岩石的封闭应力,蠕变和扩容及本构方程[J].岩石力学与工程学报,1991,10(4):299-312.CHEN Zong-ji,KANG Wen-fa,HUANG Jie-pan.On the locked in stress,creep and dilatation of rocks an d the constitutive equations[J].Chinese Jourual of Rock Mechanics and Engineering,1991,10(4):299-312.

[18]GAO H M,CHEN Y M,LIU H L,et al.Creep behavior of EPS composite soil[J].Science China Technological Sciences,2012,55(11):3070-3080.

[19]AUGUSTESEN A,LIINGAARD M,LADE P V.Evaluation of time-dependent behavior of soils[J].International Journal of Geomechanics,2004,4(3):137-156.

[20]LIINGAARD M,AUGUSTESEN A,LADE P V.Characterization of models for time-dependent behavior of soils[J].International Journal of Geomechanics,2004,4(3):157-177.

[21]LADE P V,LIU C.Experimental study of drained creep behavior of sand[J].Journal of Engineering Mechanics,1998,124(8):912-920.

[22]KARIMPOUR H,LADE P V.Creep behavior in virginia beach sand[J].Canadian Geotechnical Journal,2013,50(11):1159-1178.

[23]KARIMPOUR H,LADE P V.Time effects relate to crushing in sand[J].Journal of Geotechnical and Geoenvironmental Engineering,2010,136(9):1209-1219.

[24]KARIMPOUR H.Time effects in relation to crushing in sand[D].Washington,DC:Catholic University of America,2012.

[25]维亚洛夫 C C.土力学的流变原理[M].杜余培译.北京:科学出版社,1987.

[26]SINGH A,MITCHELL J K.General stress-strain-time function for soils[J].Journal of the Soil Mechanics and Foundations Division,1969,95:1526-1527.