大降雨条件下气压力对边坡稳定的影响研究

王继成 ，俞建霖，龚晓南，马世国

（1.浙江大学 滨海和城市岩土工程研究中心，杭州 310058；2.台州职业技术学院建工学院，浙江 台州 318000；3.宁波城建投资控股有限公司，浙江 宁波 315031）

1 引 言

降雨入渗是非饱和土边坡产生滑坡的重要因素[1]。强降雨不仅导致边坡湿润区土体重度的增加和基质吸力的降低，对于下部含有基岩的大面积浅层边坡或者地下水位较浅的边坡，强降雨还可导致坡体封闭气体压力的产生，且使土体湿润区产生封闭气泡。湿润峰下部未湿润区土体内气压势也会随着雨水的入渗不断增加[2]，增加的气压不仅降低雨水在土体的入渗率，而且增加了坡面的冲刷力度，导致坡体被侵蚀。

国内外学者研究了土体的强降雨入渗[2-15]。1983年Morel-Seytoux[5]提出，随着雨水的不断入渗，封闭气体压力不断增加，此后气体不断地重复着排出和压缩过程。此后，Grismer 等[6]做了大量的试验也验证了这一理论。Hammecker 等[7]和Latifi等[8]也通过大量的试验研究，表明入渗时湿润区下部气体会被压缩，且Latifi 等[8]研究所得的结论与Morel-Seytoux 极为接近。李媛农等[9-11]采用室内垂直一维积水入渗试验研究气阻变化的规律，揭示了土壤空气在入渗过程中的减渗效应，认为禁锢土壤气压力为表面积水深和湿润峰深度综合作用的结果。Wang 等[12-13]通过试验提出气体封闭时土体内气压变化关系，认为水体入渗过程中土体内的气体压力头存在2 个临界值。孙冬梅等[14]根据多孔介质中水、气的质量守恒定律，结合多相流理论，建立了求解饱和-非饱和渗流的水-气二相流数学模型，但该模型需采用积分形式的有限差分法和Newton-Raphson 迭代方法进行数值求解，较为不便。这些研究大多针对田间灌溉和土壤雨水入渗中的封闭气体压力。张士林[15]利用Green-Ampt 入渗模型提出了考虑气压势的入渗率公式，并研究大降雨条件下边坡的入渗问题，气压势的大小根据理想状态气体方程求得，气体排出前较为合理，但气体排除后无法继续应用。韩同春等[2]利用Wang 提出的入渗模型研究了边坡的滑坡延时效应，但两者均未考虑气压对边坡稳定的影响。

对于大面积浅层边坡，下部含有浅水位或不透水基岩层时，随着雨水的入渗气体势必被封闭并不断增大。既然强降雨条件下封闭气体压力对边坡产生一定的滑坡延时效应，那么封闭气体压力必定对边坡的稳定性产生一定程度的影响。降雨入渗条件下，现有的稳定分析模型当中一般没有考虑土壤封闭气体压力的影响，因此，本文基于前人研究的成果，将气体压力引入边坡稳定的计算模型当中，并结合算例分析和讨论了封闭气体压力的影响。

2 土体内部封闭气压力理论

降雨入渗是一个雨水对土壤中气体的驱替过程。对于大面积的浅层土体，强降雨入渗前，土壤中气体压力为标准大气压力（约10 m 水头）。雨水入渗初期，大降雨导致土体表面瞬间形成一个封闭的硬壳层[16]，随着湿润峰的不断下移，气压将不断增大。假定土体处于一个等温、均质的状态，土层中空气完全被压缩，无外溢现象发生，且有一近似水平的湿润峰，雨水入渗初期（气体排出之前）下部封闭气体压力可通过理想气体状态方程来求解：

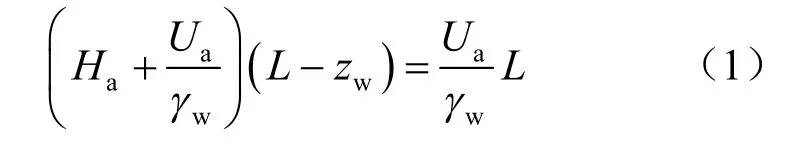
式中：Ha为湿润峰下部封闭气体压力头（超过大气压力那部分压力头）；L为土层厚度（土体表面与地下水位或不透水基岩的距离）；zw为湿润峰下移的深度；γw为水的重度；Ua为外界大气压力。式（1）简化后，得到

对于降雨入渗后期（气体开始排出阶段），土体内被限制的气体压力达到某一值，气体开始穿过湿润区直至排出地表。而气体排出后，内部压力降低，雨水进一步入渗，剩余的气体再一次被压缩，直到又一次的排出，随着雨水的入渗，土体内气体不断重复压缩和排出过程。研究气压边坡的影响，关键是确定气压力的形式，国内外学者进行了许多试验研究和理论分析。

Wang 等[13]1998年通过试验提出的气体封闭时土体内气压变化形式，认为水流入渗过程中土体内的气体压力水头Ha存在2 个临界值，当土层内气压升高到上临界值时，气体突破上部土体而排出，称为气体突破压力（air-breaking value）；当压力减小到下临界值时，排气通道重新被水封闭，称为气体闭合压力（air-closing value）。

韩同春等[2]比较支持Wang 的观点，在其基础上将平均气压力形式引入到边坡的降雨入渗研究当中，气压力头为

式中：h′=(hab+hwb)/2，hab为土体的进气值水头，hwb为土体的进水值水头；zw为湿润峰的深度（假设湿润峰近似水平）；h0为土体表面的积水深，对于边坡的研究，由于坡面径流，积水深一般假设为0。

韩同春等研究表明气压力对滑坡的延时效应显著。式（3）表明，气泡开始排出后，气压力与湿润峰深度呈线性关系，将不断增大。但Wang 所研究的土质为均质细砂，湿润峰假设为一绝对平面，在边坡或者其他自然土壤中是不现实的。气压力必然和最小湿润峰深度有关，对于不同的土质很难确定。

李援农等[11]1997年对均质土壤积水入渗的气阻变化规律进行研究，讨论了气阻对入渗速率的影响，并在2005年利用自制的一维入渗仪对禁锢土壤空气进行研究[10]，认为禁锢土壤空气压力为土壤表面积水深度H与湿润层厚度 zw综合作用的结果，并给出入渗稳定后该压力的大小关系为，a≈2.1H（a为禁锢土壤空气压力），并将其引入到Green-Ampt模型。

但是，该压力形式由试验数据拟合得到，且认为气体压力最终稳定为一定值，形式上只与表面积水深有关，没有考虑到土壤孔隙大小和湿润峰的深度等因素，显然不甚合理，在不同的土质和试验条件下适用性有待验证。

Latifi 等[8]1994年进行了双层土的一维入渗试验，认为双层土内气体压力与土的渗透系数、土体进气值以及封闭的深度有关。之后的分析得出，气体的最大压力头值——突破压力头为大气压加上相应土体的进气值水头(Hat+He)，Hat、He分别为大气压力头和土体的进气值水头。气体突破后压力降为(He+d)，d为某一水头常数，与土质有关。但文中并没有给出d 值大小的表达形式。

由于封闭气压力往往是大降雨或大面积灌溉引起的，同时土体下部含有浅水位，内部气体被限制在接近饱和的湿润面与浅水位之间。Grismer 等[6]1994年通过大量的试验，证明了Morel-Seytoux[5]提出的封闭气压形成(H+Hc)，H为积水水头，Hc为一水头大小等于(1.00～1.21) hd的值，hd为进气水头值。气压力在雨水入渗的初期不断增大，之后达到最大值(H+Hc)。此后随着气体不断排出和压缩，气压力基本稳定在 H+Hc，并分别采用不同的土质进行试验分析，如图1 所示。

图1 不同砂土入渗条件下气压力变化曲线Fig.1 Air pressure curves in different sands under infiltration

由图1 可以看出，所测得的气压力值近似等于与土体相关的(H+Hc)值。表1为不同的土质或不同的限制深度下气体突破时气压力头测量值和预测值的对比结果[6]。由表可以看出，预测的气压力值与突破后测量的稳定气压力值基本吻合，也就是说可以近似得到以下关系：

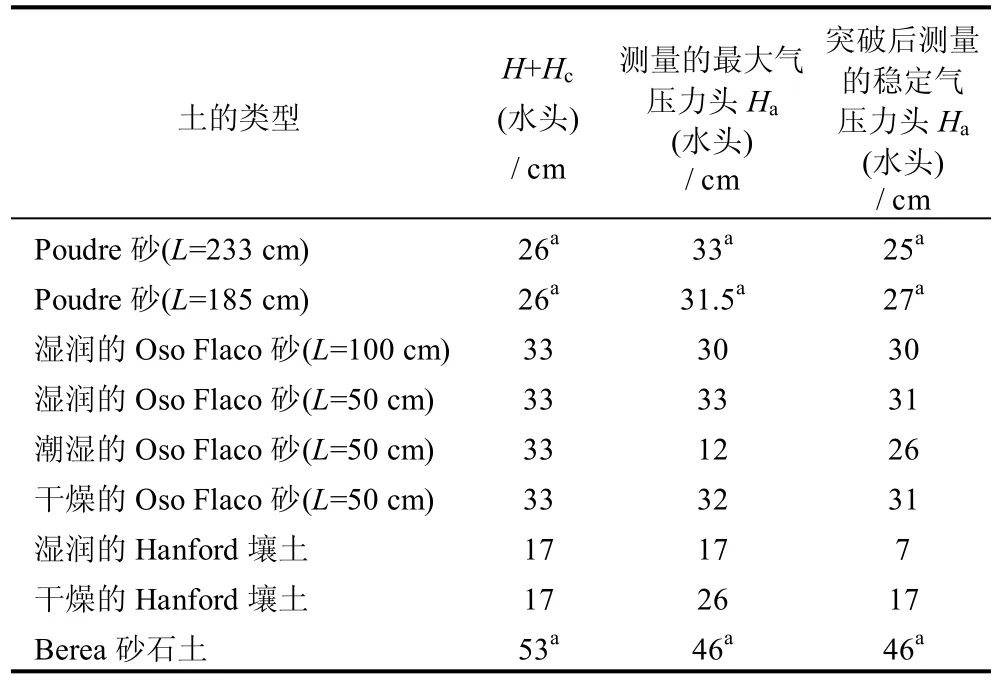
表1 不同土质气体突破时气压力头测量值和预测值的对比[6]Table 1 Comparison of predicted and measured values of air pressure head required for breakthrough in various soils[6]

由于Hc=(1.00～1.21) hd，为简化计算并引入稳定计算模型中可近似取其平均值，即Hc取1.105 hd。考虑式（4）和测量结果具有较好的一致性，对于大面积浅层边坡，当下部还有浅水位或不透水基岩层时，即可利用式（4）研究考虑气压力影响下的边坡稳定分析问题。

3 考虑气压力边坡稳定分析模型

在大降雨入渗条件下，非饱和土无限边坡发生浅层破坏最为常见，且多为平行于边坡表面破坏[2]。对于大面积无限长边坡，降雨入渗条件下湿润峰处基质吸力降低，同时湿润峰下部气体压力不断增大，气体产生的顶托力将使得最危险面极有可能发生在湿润峰处。由于气压力的存在，发生滑坡的时间不一定推迟。边坡在湿润峰处的安全系数随着下部封闭气压的增加，在一定程度上有可能会降低。

如图2 所示的边坡，L为土层厚度，W为滑体单位宽度土条的重量，σn为单位宽度土条底部的正应力，τm为单位宽度土条底部的下滑力，α为边坡角度，γm为考虑湿润区气泡影响下的非饱和重度，γ0为非饱和土体的初始重度。湿润峰处安全系数可由湿润区总的抗滑力与下滑力之比来求解，湿润峰处抗滑力采用非饱和土的抗剪强度公式求解，下滑力即为湿润区土体的重度沿坡面的分量，即根据非饱和土Mohr-Coulamb 破坏准则[17]和极限平衡法得到边坡稳定安全系数：

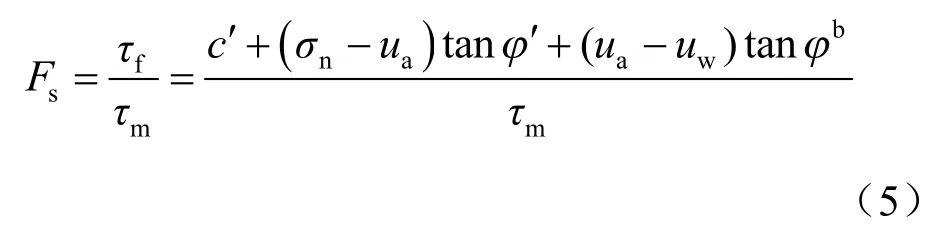
式中：τf为非饱和土抗剪强度；c′、φ′分别为土的有效黏聚力和内摩擦角；φb为抗剪强度随基质吸力变化的吸力摩擦角；ua为孔隙气压力；(ua-uw)为土体湿润峰处的基质吸力值。

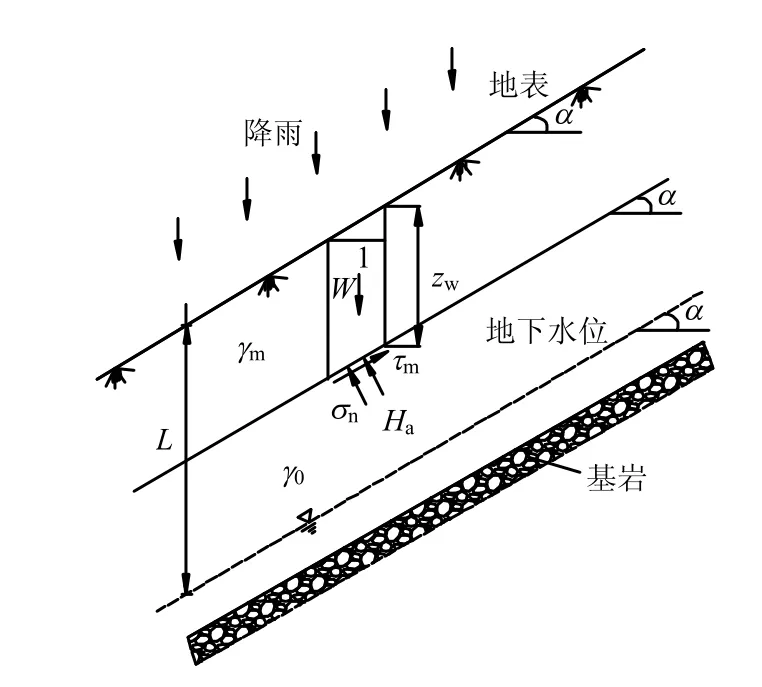
图2 下部为基岩的浅层边坡分析图Fig.2 Sketch of shallow slope with bedrock beneath

当考虑封闭气压力（超过大气压力那部分压力头）影响时，大降雨条件下含气泡的湿润区土体近似饱和，湿润峰以上土体基质吸力极小，作近似为0 处理。因此，式（5）可改写为

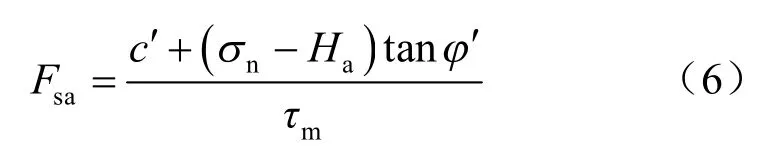
式中：Fsa为考虑气压影响的边坡的安全系数。

3.1 不考虑封闭气压时的稳定分析模型

图3为不考虑气压力条件下土条受力分析图。由于坡面径流，因此假设积水水头为0，H=0。在强降雨条件下，当考虑湿润区封闭气泡的影响，湿润区采用非饱和重度 γm来计算得到如下稳定分析模型：

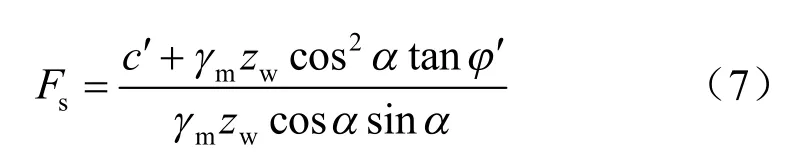
不考虑湿润区封闭气泡的影响时，湿润区采用饱和重度 γt来计算：

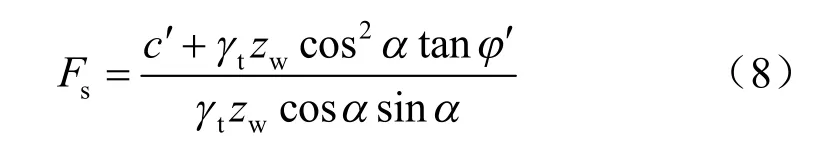
式中：γt为土的饱和重度。

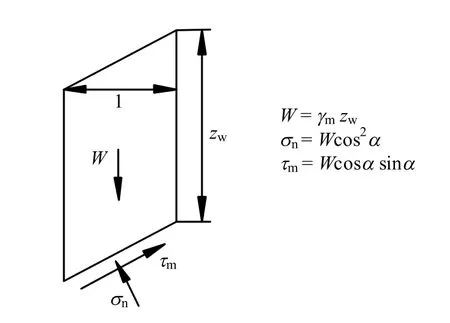
图3 不考虑气压力土条受力分析图Fig.3 Sketch of soil slice without air pressure

3.2 考虑封闭气压时的稳定分析模型

图4为考虑气压力影响下土条受力分析图。Wang 对不同的土质汇总分析表明[13]，在降雨入渗初期的气体压缩阶段，即气体排出之前的时间较短，尤其对于砂性土可忽略不计，在大降雨条件下，对于边坡的研究可忽略气压增加的时段。将式（4）代入式（6），湿润区土体重度采用非饱和重度 γm来计算，由于坡面径流，假设无积水发生，得到如下考虑封闭气压影响下的稳定分析模型：

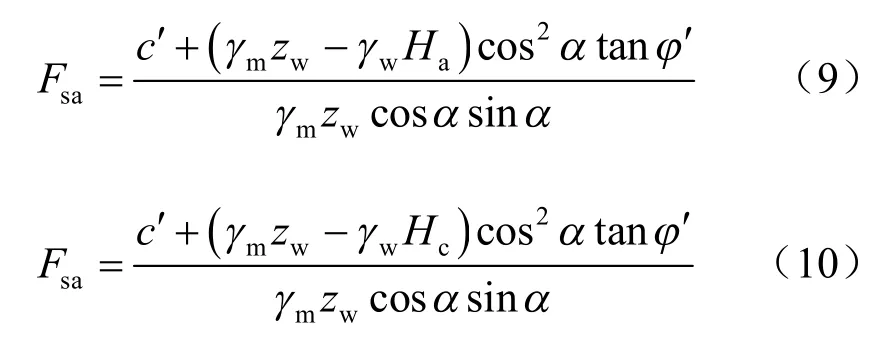
图4 考虑气压力土条受力分析图Fig.4 Analysis chart of soil slice with air pressure

Wang（1997年）在数据分析当中认为，在砂性土封闭条件下湿润区气体饱和度 Snw,c比自由排出条件下湿润区气体饱和度 Snw,o大7%左右[12]。因此，对于砂性土边坡，为简化场地条件下测量工作，可近似认为 γt=γm，不仅便于计算和预测，且所得结果偏于安全。因此，式（10）近似可改写为

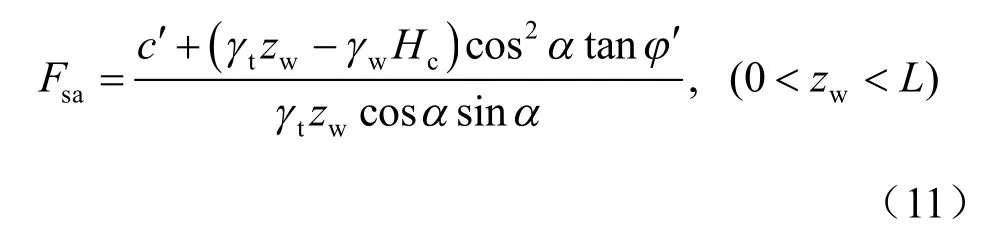
当湿润峰到达基岩面或者地下水位处时，即zw=L，此时气压力消失，式（11）将不再适合计算边坡的稳定性。无气压力时，采用式（8）求解此刻边坡在 zw=L 处的安全系数：

这里引入一个气压力影响率η，定义为

气压力影响率更能直观地反映入渗的各个阶段气压力对边坡安全系数的降低程度。对于不同土质坡体，由于颗粒尺寸、孔隙比和含水率的不同，气压力也会不同，那么可以通过气压力影响率的大小，初步判断该类型边坡的稳定分析是否需要考虑气压的影响，对降雨入渗条件下边坡的稳定分析和滑坡预测具有较好的指导意义。

4 算例分析与讨论

为更好的了解大降雨条件下封闭气压对边坡稳定的影响，假设有一无限长风化土浅层边坡，上覆L=50 cm 厚的风化土层，下部为不透水基岩层，边坡角度为33.70（坡比为1:1.5），如图2 所示，稳定性分析参数见表2[2]。假设强降雨条件下，由于边坡坡面径流，无积水产生，H=0。由于Hc大小为（1.00～1.21）倍的进气值 hd（hd为进气值），因此取平均值Hc=1.105 hd=16.575 cm。

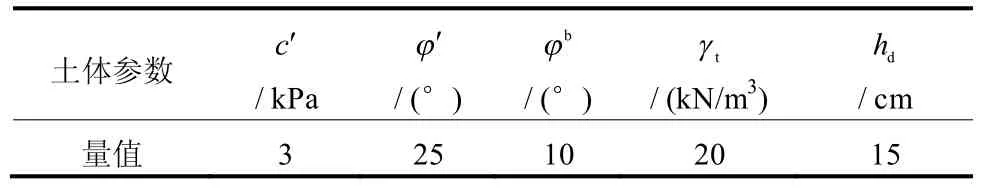
表2 非饱和土体计算参数[2]Table 2 Parameters of unsaturated soil[2]

对于风化土边坡，可近似认为 γt=γm，分别应用传统的稳定计算方法式（8）和本文考虑气压影响下的计算方法式（11）、（12），可得到的计算结果如图5 所示。

图5 Fs-zw变化曲线Fig.5 Fs-zwcurves

由图5 可以看出，当湿润峰达到20 cm 时，传统不考虑气压力方法计算的安全系数Fs=2.32，本文计算的安全系数Fs=2.04；当湿润峰达到49 cm 时，传统不考虑气压力计算的安全系数Fs=1.36，本文计算的安全系数Fs=1.23。可见，当考虑气压力影响时边坡的安全系数降低明显，对于采用传统的稳定计算方法计算边坡的稳定时存在一定的风险，本文考虑气压力的稳定分析方法偏于安全。图6为气压力影响率η 随湿润峰 zw的变化曲线。由图可以看出，随着 zw的不断下移，η 逐渐降低。η=17.1%，当湿润峰下移至接近边坡底部基岩处（zw≈50 cm），η 低至8.4%，但对于浅层风化土边坡，气压力的影响依然不可忽略。

图6 气压力影响率随湿润峰的变化曲线Fig.6 Effect ratio of air pressure with wetting peak curve

5 结 论

（1）对于大面积浅层边坡，下部若有浅水位或不透水基岩层时，大降雨将导致下部气体被封闭。本文总结了国内外对封闭气压力的研究成果，并对封闭气压力的形成做了简单的分析，提出可取Hc=1.105hd的气压力头大小来研究风化土边坡的稳定性。

（2）结合非饱和土的Mohr-Coulamb 破坏准则和极限平衡法，将封闭气压力引入到边坡稳定分析中。通过对比传统的无限边坡的稳定分析方法，表明封闭气压力显著降低了边坡的安全系数。本文提出了气压力影响率概念，可更好的反映封闭气压的对边坡稳定的影响，对于浅层风化土边坡气压力的影响不可忽略。

封闭气压力对边坡的稳定影响显著，由于缺乏有效的现场和试验数据，不同土质的最大突破压力值无法确定。今后尚需更多的研究来解决气压力影响率与土体孔隙比、含水率等参数的关系以及入渗初期气体最大突破压力值对边坡稳定的影响。

[1]陈祖煜.土质边坡稳定分析:原理、方法、程序[M].北京:中国水利水电出版社,2003.

[2]韩同春,马世国,徐日庆.强降雨条件下气压对滑坡延时效应研究[J].岩土力学,2013,34(5):1360-1366.HAN Tong-chun,MA Shi-guo,XU Ri-qing.Research on delayed effect of landslides caused by air pressure under heavy rainfall[J].Rock and Soil Mechanics,2013,34(5):1360-1366.

[3]林鸿州,于玉贞,李广信,等.降雨特性对土质边坡失稳的影响[J].岩石力学与工程学报,2009,28(1):198-204.LIN Hong-zhou,YU Yu-zhen,LI Guang-xin,et al.Influence of rainfall characteristics on soil slope failure[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):198-204.

[4]周家文,徐卫亚,邓俊晔,等.降雨入渗条件下边坡的稳定性分析[J].水利学报,2008,39(9):1066-1073.ZHOU Jia-wen,XU Wei-ya,DENG Jun-ye,et al.Stability analysis of slope under the condition of rainfall infiltration[J].Journal of Hydraulic Engineering,2008,39(9):1066-1073.

[5]MOREL-SEYTOUX H J.Infiltration affected by air,seal,crust,ice and various sources of heterogeneity[C]//Proceedings of ASAE National Conference on Advances in Infiltration,Chicago(special problems):[s.n.],1983:132-146.

[6]GRISMER ME,ORANG MN,CLAUSNITZER V,et al.Effects of air compression and counterflow on infiltration into soils[J].Journal of Irrigation and Drainage Engineering,1994,120(4):775-795.

[7]HAMMECKER C,ANTONINO A C D,MAEGHT J L,et al.Experimental and numerical study of water flow in soil under irrigation in northern Senegal:Evidence of air entrapment[J].European Journal of Soil Science,2003,54(3):491-503.

[8]LATIFI H,PRASAD S N,HELWEG O J.Air entrapmentand water infiltration in two-layered soil column[J].Journal of Irrigation and Drainage Engineering,1994,120(5):871-891.

[9]李援农,吕宏兴,林性粹.土壤人渗过程中空气压力变化规律的研究[J].西北农业大学学报,1995,23(6):72-75.LI Yuan-nong,LI Hong-xing,LIN Xing-cui.Regularities of air pressure changes in soil infiltration[J].Journal of the Northwestern Agricultural University,1995,23(6):72-75.

[10]李援农,费良军.土壤空气压力影响下的非饱和入渗格林-安姆特模型[J].水利学报,2005,36(6):733-736.LI Yuan-nong,FEI Liang-jun.Green-Ampt model for unsaturated infiltration affected by air pressure entrapped in soil[J].Journal of Hydraulic Engineering,2005,36(6):733-736.

[11]李援农,林性粹.均质土壤积水入渗的气阻变化规律及其影响[J].土壤侵蚀与水土保持学报,1997,11(3):51-54.LI Yuan-nong,LIN Xing-cui.Regularity of the soil airresistance change and its influences under wateraccumulated infiltration in the homogenous soil[J].Journal of Soil Erosion and Soil and Water Conservation,1997,11(3):51-54.

[12]WANG Z,FEYEN J,VAN GENUCHTEN MT,et al.Air entrapment effects on infiltration rate and flow instability[J].Water Resources Research,1998,34(2),213-222.

[13]WANG Z,FEYEN J,NIELSEN D R,et al.Two-phase flow infiltration equations accounting for air entrapment effects[J].Water Resources Research,1997,33(12):2759-2767.

[14]孙冬梅,朱岳明,张明进.降雨入渗过程的水-气二相流模型研究[J].水利学报,2007,38(2):150-156.SUN Dong-mei,ZHU Yue-ming,ZHANG Ming-jin.Water-air two-phase flow model for numerical analysis of rainfall infiltration[J].Journal of Hydraulic Engineering,2007,38(2):150-156.

[15]张士林.大降雨强度下雨水入渗规律研究[J].岩土工程技术,2003,18(5):281-285.ZHANG Shi-lin.The research of infiltrating regulation under rainstorm[J].Geotechnical Engineering Technique,2003,18(5):281-285.

[16]BEN-DOR E,GOLDLSHLEGER N,BENYAMINI Y,et al.The spectral reflectance properties of soil structural crusts in the 1.2-to 2.5-μm spectral region[J].Soil Science Society of America Journal,2003,67(1):289-299.

[17]FREDLUND D G,MORGENSTERN N R,WIDGER R A.The shear strength of unsaturated soil[J].Canadian Geotechnical Journal,1978,15(3):313-321.