基于属性掌握概率的认知诊断模型

毛秀珍

(四川师范大学 教育科学学院, 四川 成都 610066)

1 预备知识

认知诊断理论是基于项目反应理论的新一代测量理论.它通过分析学生的作答反应获得学生知识结构中优势与不足的诊断信息,在教育实践中发挥着重要作用.一方面,根据认知诊断理论分析的属性层级关系编制测验能大大提高测验的信度和效度；另一方面,根据属性层级关系分析的学习之路能为选取快速有效的学习方法和教学策略提供指导.因此,认知诊断理论得到了大量的研究与实践[1-4].一般而言,认知诊断评估包含以下2个步骤.第一,从认知心理学角度分析学生作答项目时采用的知识和技能.第二,根据心理计量学模型拟合测验反应,据此推论被试的知识状态和项目特征.由此可见,认知诊断模型是认知诊断研究与应用的基础.

到目前为止,研究者提出了大量认知诊断模型.D. Bolt[5]将认知诊断方法划分为4个广义的类别：潜在类别模型、连续潜在特质模型、基于贝叶斯网络的认知诊断模型、规则空间方法及其变式:属性层级方法.特别地,“确定性输入,噪音‘与’门”模型(DINA)模型和“噪音输入,确定性‘与’门”模型(NIDA)模型属于潜在类别模型[6].首先,DINA模型假设测验要求的属性之间不具有补偿关系,并用猜测和失误参数模拟作答过程的随机因素,即si表示当被试掌握项目i考查的所有属性时错误作答项目的概率;表示当被试至少有一个项目i考查的属性没有掌握时正确作答项目i的概率.于是,其项目反应函数表示为

P(Xij=1|αj,si,gi)=

(1)

(1)式中αj=(αj1,αj2,…,αjK)为被试j的知识状态或称为属性掌握模式.如果他(她)掌握属性i,则αji=1,否则αji=0.另外

qik(i=1,2,….N,k=1,2,…,K)为QN×K矩阵的元素,N为测验包含的项目个数,K等于测验考查的属性个数.qik只取1或0,如果项目i考查属性k,则qik=1,否则qik=0.DINA模型可以区分同一被试在包含相同属性的不同项目上的反应.然而对每个项目,它只能将所有被试的作答情况分为两类.当被试掌握项目i考查的所有属性时ηij=1,其正确作答项目的概率为1-si;如果被试j至少有一个项目i考查的属性没有掌握,则其正确作答项目i的概率为gi.因而,DINA模型不能精细地区分不同属性掌握模式的被试正确作答同一项目的概率,降低了项目的区分度[7].

其次,NIDA模型通过对每一属性k分别定义猜测参数gk和失误参数sk,并假设属性运用满足局部独立性,建立项目反应函数如下

P(Xij=1|αj,sk,gk)=

(2)

于是,NIDA模型能区分不同属性掌握模式的被试对同一项目的作答概率,提高了项目的区分能力.但是,NIDA模型假设项目特征完全决定于其所考察的属性,忽视了包含相同属性的不同项目之间的差异[7],从而使得同一被试正确作答包含相同属性的不同项目的概率相等.

另外,文献[8]介绍了规则空间方法(RSM).该方法分为特征提取和统计分类2个阶段[8].第一阶段包括以下5个步骤：首先,领域专家通过分析解题过程中的认知结构形成关于属性的假设；其次,根据属性的定义对题目考查的属性进行编码,建立属性与题目之间对应关系的Q矩阵；再次,运用Q矩阵分析邻接矩阵A、可达矩阵R和理想知识状态矩阵E；第四,根据矩阵E和Q计算理想作答反应模式；最后,建立规则空间并将理想作答反应和实际作答反应映射为规则空间的点.第二阶段借助多元统计或贝叶斯方法实现被试知识状态的诊断分类.该方法有严密的理论基础,涉及项目反应理论(IRT)和多元统计理论.但它需要多个步骤才能完成对属性掌握概率的分析,同时每一步的结果都会影响下一步运算和最终结果,从而增加诊断误差.

鉴于上述常用认知诊断方法的不足,本文将在模型扩展、模型求解和模型效能3个方面做一些探索.

2 属性掌握概率认知诊断模型的建立和参数估计方法

2.1属性掌握概率认知诊断模型(AMPM) 本文定义属性掌握概率为：对考察属性k的N个项目,假设被试正确作答项目中该属性部分的项目个数为n,则他正确作答属性k的频率为n/N.当项目个数N趋于无限大时,频率的稳定值定义为属性k的掌握概率,它在测验中体现为正确作答属性k的概率.

假设测验一共考察K个属性,则被试j的属性掌握概率模式表示为K维向量

MPj=(MPj1,MPj2,…,MPjk,…MPjK),

其中MPjk(k=1,2,…,K)取值于[0,1],表示被试j掌握第k个属性的概率.在Q矩阵前提下,定义失误参数si表示被试因失误错误作答项目i的概率,即

猜测参数gi为被试因猜测等因素正确作答项目i的概率,即

si和gi不随被试的不同而发生变化.假设属性运用满足局部独立性,AMPM模型表示为

(3)

该模型综合了被试的知识结构、项目特征和作答过程等信息拟合项目反应.当属性掌握概率取1或0时,AMPM和DINA模型一致.与DINA、NIDA和RSM相比,AMPM具有以下几个优点：1) 它能区别考察相同属性的不同项目的特征；2) 它能区分不同属性水平的被试对同一项目的作答概率；3) 属性掌握概率取值于区间[0,1],能恰当表征应用知识的能力；4) 它以DINA模型为基础,不增加模型参数的情况下,直接分析属性掌握概率,为分析被试的知识状态提供了一种新的视角和方法；5) 参数估计方法简单,具有实践可行性.

2.2参数估计

2.2.1方法和工具 马尔科夫链蒙特卡洛(MCMC)算法简单,不仅能描述具有随机性质事物的特点,而且收敛速度与问题的维数无关,从而在估计心理计量模型参数中得到了广泛运用[9-10].于是,本文运用MCMC方法并采用M-H吉布斯算法[9]模拟抽样,以MATLAB为工具,自编程序进行参数估计.

2.2.2模型参数的先验分布 文献[10]在估计模型参数时均假设项目参数服从贝塔分布[11].另外,当样本量很大时,先验分布的选择不会对结果产生很大影响.于是,本文假设项目参数的先验分布服从4-Beta(γ,η,a,b)分布,即si～4-Beta(γs,ηs,as,bs)和gi～4-Beta(γg,ηg,ag,bg).

借鉴文献[12-13],本文假设属性掌握概率向量服从多变量广义贝塔(MGB)分布.假设X0,X1,…,XΓ是独立取自伽马分布的随机变量,即

Xi～Γ(αi,βi),i=0,1,2,…Γ.

通过变换Y0=X0,

Yi=Xi/(X0+Xi),i=0,1,2,…,Γ,

得到一组随机变量Y0,Y1,…,YΓ.文献[12]证明,随机变量(Y0,Y1,…,YΓ)服从参数为α0,α1,λ1,…,αi,λi,…,αΓ,λΓ的MGB分布,即

(Y0,Y1,…,YΓ)～

其中λi=βi/β0,i=1,2,…,Γ.(Y0,Y1,…,YΓ)的联合概率密度函数为

0≤yi≤1.

(4)

2.2.3MCMC算法 将各被试参数和项目参数分别组块,按(MP1,MP2,…,MPJ,s1,g1,s2,g2,…,sI,gI)顺序抽取参数.具体地,第t次迭代的MCMC算法如下.

(5)

以及

去的路上，四个人说说笑笑，回来的路上，四个人都有点沉默。之前，只是对未来很茫然，这一刻，却切切实实全转化成了压力。

项目参数的接受概率为

(6)

3 模拟研究

模拟研究的目的是验证MCMC方法估计模型参数的准确性和稳定性.

3.1方法

3.1.1反应数据的产生 首先,根据文献[4]中20个包含8个属性的分数减法项目,确定模拟研究的Q矩阵,见表1.其次,根据文献[10],确定项目参数服从4-Beta(1,2,0,0.25)分布.相应地,产生20组随机数作为项目参数,见表2中s和g对应的列.

然后,随机确定MGB(2,7.5,1,5,1,8,1,7,1,5.5,1,6,1,13,1,9,1)作为属性掌握概率向量的分布,产生1 000个被试的属性掌握概率向量.

最后,固定Q矩阵、项目参数以及被试参数的分布,一共模拟生成26个数据集.每个数据集包含1 000名被试在考察8个属性的20个项目上的反应.

3.1.2参数估计 随机产生均匀分布的随机数作为模型参数的初始值.每次估计迭代5 000次,采用M-H吉布斯算法模拟抽样,计算最后3 500次抽样的平均数作为参数的估计值.

表 1 模拟研究的项目结构Q矩阵

3.2结果

表 2 模拟研究中项目参数的结果

当参数取值于[0,1]且MAD小于0.1时,估计结果较好[15].因此,从表3可知,被试能力估计的准确性和稳定性较好.另外,被试参数中估计最好的是属性a7,较差的是属性a6、a2和a5.分析Q矩阵,发现考察属性a7的项目最多,并且有2个项目只考察属性a7.考察属性a6的项目最少,涉及属性a6的2个项目分别考察了3个和4个属性,且包含了属性a2、a5和a4.可见,项目考察的属性个数和考察每个属性的项目个数会影响属性估计的准确性.

4 实证研究

4.1数据描述实证研究采用文献[16]中40个分数减法项目的反应数据,Q矩阵见表4.他们将40个项目对等地分成2组平行测验,各有536名学生参加测验.然后,他们根据A、B的2种解题策略,分别对2组学生的反应做了分析.根据方法B,文献[16]表明2组中分别有20名和14名学生没有被分类到任何一个理想属性掌握模式.因此2个数据集分别包含516名和522名学生的属性掌握概率.

表 3 模拟研究中被试参数的结果

表 4 20个分数减法项目的Q矩阵

本文利用AMPM分析其中516名学生的属性掌握概率.

4.2参数估计除了属性掌握概率分布的超参数外,参数估计的方法和步骤与模拟研究一致.根据多变量广义贝塔分布的特点和数学教师对这8个知识属性的先验判断假设属性掌握概率的先验分布为MP～MGB(0.5,0.6,0.9,1.5,1.3,1.1,0.8,0.6,0.2,1,0.7,1.1,0.6,0.9,1.4,1.7).

4.3结果10次独立估计的项目参数的平均值和标准差,见表5.项目参数取值都小于或等于0.23,模型拟合较好.参数估计与文献[10]的结果一致.几乎所有的标准差都小于0.01,结构参数的估计稳定.

对被试参数,采用2个指标考察AMPM与文献[16]中运用RSM方法所得结果的一致性,见表6.第一,对每个属性掌握概率,计算AMPM和RSM分析结果的相关系数r.第二,根据AMPM的估计结果,以0.5作为临界值将被试属性掌握概率划分为掌握和未掌握.计算AMPM与RSM在每个属性上的分类一致比率p,即对所有被试在各个属性上同时被判断为掌握和未掌握的人数比率.

实证分析表明,AMPM和RSM有关属性掌握概率和属性掌握与否的结果都具有较高的一致性.对每个属性,属性掌握概率的相关系数和属性分类一致比率都大于0.82,其中,属性a6和a7的分类一致性稍低于其它属性.根据项目Q矩阵,平均每个项目考察3.25个属性.分别有3个项目考察属性a6和a7,并且这些项目都考察了3个以上的属性.而考察其它属性的项目都多于3个.可见,项目考察属性的个数与考察各属性的项目个数都会影响2种方法分析结果的一致性.这与模拟研究结论一致.

5 结论与讨论

表 5 分数减法数据中项目参数的估计值和标准差

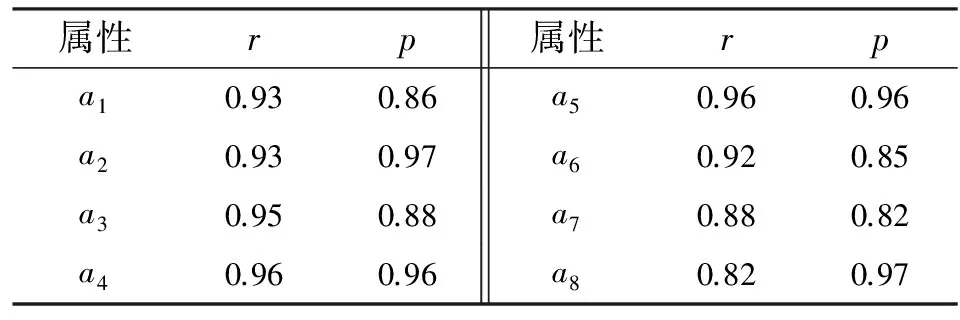
表 6 AMPM和RSM在各属性上的相关和分类一致性

5.1研究结论已有诊断方法大都假设知识的掌握和应用之间是确定性关系,即一旦掌握某知识,就能正确作答该知识.实际上,掌握一个知识点比正确应用该知识点更容易.正确应用知识与掌握知识的熟练程度相关.因此,本文从分析属性掌握概率出发,扩展了诊断模型的研究.

首先,基于RSM和DINA模型,建构了属性掌握概率的认知诊断模型.该模型形式简洁,符合实际.它不仅能区别考察相同属性的不同项目的特征,还能区分所有被试对同一项目的作答概率,克服了已有模型的不足.另外,根据属性掌握概率,依据一定标准还能获得被试的知识结构.但该模型还存在一些不足之处,例如,作答概率的估计容易受到结构参数的影响；当项目包含的属性过多时,模型拟合度降低.其次,模拟研究表明,MCMC方法估计项目参数的准确性和稳定性较好.最后,实证研究表明AMPM与RSM的结论比较一致,从而为模型的信度和效度提供了依据.

5.2讨论

5.2.1模型比较 认知诊断通过对测验结构和作答反应的分析,不仅获得每个学生整体能力的高低,而且能把握他们具备的知识结构和能力水平,并建构知识获得的最佳途径.随着认知诊断理论的兴起,以模型为基础的认知诊断方法层出不穷.诊断模型在追求形式简洁和高诊断性能的平衡中得到丰富和发展.实际上,模型与数据的拟合程度是选择与应用模型的关键问题.因此,不同模型的比较是今后研究的一个方向.

5.2.2探索多级计分项目的认知诊断模型 目前大部分诊断模型均基于二级计分项目,适用于多级计分项目的认知诊断模型还比较少.实际上,各类型考试均基于多种形式的项目并且大部分属于多级计分项目.因此,探索适用于多级计分项目的认知诊断模型或在已有模型的基础上扩展适合多级计分项目的认知诊断模型具有重要意义.

5.2.3认知诊断模型的实践应用 目前已发展了多种认知诊断方法,国外还开展了广泛的实践研究.针对国内坏境,大部分研究都将规则空间方法用于分析实际问题并得到比较满意的结果.因此,未来研究有必要检验其它认知诊断模型的实践效应.

[1] Embretson S E. A multidimensional latent trait model for measuring learning and change[J]. Psychometrika,1991,56(3):495-515.

[2] Gierl M J, Zheng Y, Cui Y. Using the attribute hierarchy method to identify and interpret cognitive skills that produce group differences[J]. J Educational Measurement,2008,45(1):65-89.

[3] Henson R, Roussos L, Douglas J, et al. Cognitive diagnostic attribute-level discrimination indices[J]. Applied Psychological Measurement,2008,32(4):275-288.

[4] Tatsuoka K K. Cognitive Assessment: an Introduction to the Rule Space Method[M]. New York:Taylor & Francis Group,2009.

[5] Bolt D. The present and future of IRT-based cognitive diagnostic models (ICDMs) and related methods[J]. J Educational Measurement,2007,44(4):377-383.

[6] Junker B W, Sijtsma K. Cognitive assessment models with few assumptions, and connections with nonparametric item response theory[J]. Applied Psychological Measurement,2001,25(3):258-272.

[7] Templin J L, Henson R A, Templin S E. Robustness of hierarchical modeling of skill association in cognitive diagnosis models[J]. Applied Psychological Measurement,2008,32(7):559-574.

[8] 余娜,辛涛. 规则空间模型的简介与述评[J]. 考试研究,2007(9):14-19.

[9] Patz R J, Junker B W. A straightforward approach to Markov Chain Monte Carlo methods for item response models[J]. J Educational and Behavioral Statistics,1999,24(2):146-178.

[10] de la Torre J, Douglas J. Higher-order latent trait models for cognitive diagnosis[J]. Psychometrika,2004,69(3):333-353.

[11] 张普能,李亮. 多线性分数次积分算子在Herz型Hardy空间中的有界性[J]. 四川师范大学学报:自然科学版,2013,36(5):721-725.

[12] 任静静,徐艳艳,陈广贵. 学习理论中的MLP方法[J]. 四川师范大学学报:自然科学版,2013,36(2):247-251.

[13] Tatsuoka C. Data analytic methods for latent partially ordered classification models[J]. J Royal Statistical Society,2002,C51(3):337-350.

[14] Gleman A, Rubin D B. Inference from iterative simulation using multiple sequences[J]. Statistical Science,1992,7(4) 457-511.

[15] 李峰. 无锚题测验的链接-规则空间模型的途径[D]. 北京:北京师范大学,2009.

[16] Tatsuoka K K. Architecture of knowledge structures and cognitive diagnosis: a statistical pattern recognition and classification approach[C]//Nichols P D, Chipman S F, Brennan R L. Cognitively Diagnostic Assessment. Hillsdale:Erlbaum,1995:327-359.