基于SolidWorks的减摇鳍摇臂结构分析与改进

曾晓华,宋 飞,唐 成,彭利坤

(1.海军工程大学 动力工程学院,湖北 武汉 430033; 2.海军训练舰支队司令部,辽宁 大连 116011)

0 引 言

减摇鳍是舰船常用的一种主动式减摇装置。在减摇鳍升力和波浪力等多种载荷的联合作用下，易产生大变形和损坏，危害舰船的安全性。该装置正常工作对舰船的适航性、安全性及其他设备的正常使用起着积极的作用[1]。为了提高减摇鳍系统的可靠性，本文结合维修实践中某船出现的减摇鳍摇臂断裂故障，对摇臂受力情况进行理论分析及仿真研究，探究摇臂断裂故障的深层原因，并提出优化改进建议，以避免类似事故再次发生。

1 减摇鳍摇臂受力分析

摇臂除有销孔和槽外，耳环与摇臂本体之间存在结构突变，因此存在应力集中σ1；由于摇臂与鳍轴为过渡配合，因此在安装维修时还会产生安装动应力σ2。如图1所示，在油缸带动摇臂来回摆动过程中，摇臂由于受交变载荷作用产生交变应力σ3；当油缸运动超限时，驱动油缸带着摇臂撞击限位块e产生冲击应力σ4[2]。

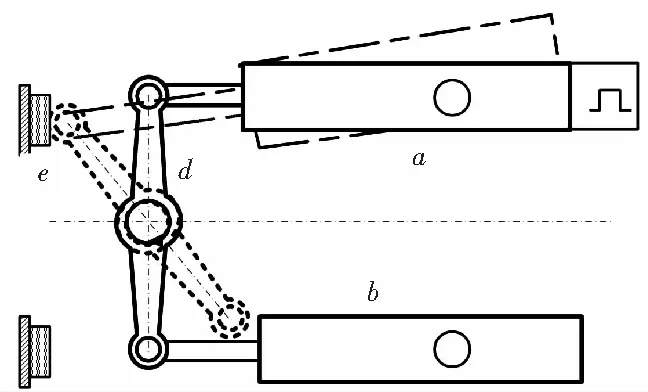
图1 减摇鳍传动机构图Fig.1 The transmission mechanism of fin stabilizer

1)结构缺陷产生应力集中

摇臂在靠近耳环处结构发生突变，而在结构突变处会产生应力集中。摇臂材料为铸铁，属于脆性材料，其强度受应力集中影响较大，在交变载荷的作用下，疲劳裂纹总是从构件内应力最大处首先形成。摇臂应力集中处局部应力很大，疲劳裂纹也往往在这里产生，使该处疲劳极限降低最终发生断裂[3-5]。

2)维修保养产生动应力

减摇鳍维修时，由于鳍轴与摇臂通过键进行过渡配合，拆解保养困难，在装拆过程中经常要对摇臂进行敲击；此外减摇鳍基座与水平面存在一定夹角，且鳍座盖板将摇臂及油缸的大部分遮盖，活塞杆联轴节与摇臂耳环很难准确对正，装拆时也难免对摇臂耳环等进行敲击、撬动。上述操作产生的冲击载荷可使摇臂内的应力增大几倍甚至几十倍，这种由动载荷产生的应力称为动应力，动应力达到一定数量级时，构件就会产生裂纹。

3)运动超限产生动应力

正常情况下，摇臂会在一定的角度范围内转动，但当控制系统失灵导致驱动油缸运动超限时，摇臂会随着驱动油缸一起撞击机械限位块e产生动应力而影响摇臂的使用寿命，严重时就会使摇臂产生裂纹甚至断裂。短时间、小量过载不会引发材料内部裂纹的产生或发展，但长时间、多次发生的撞击将会降低材料的疲劳极限，甚至产生裂纹并不断发展直至最后断裂。

4)疲劳损伤

当减摇鳍正常工作时，驱动油缸a与b通过摇臂d、鳍轴c带动舷外的鳍转动，以产生足够的稳定力矩去反抗波浪力矩。当大风浪来袭时，风浪对鳍的作用力通过鳍轴传给摇臂，而油源则会给油缸提供足够的反作用力来保持鳍的平衡，由于风浪变化无规则，此时在摇臂与油缸活塞杆交接处就会产生冲击力，在交变应力和不规则的冲击力作用下，摇臂中应力最大处或材料有缺陷的位置就会产生细微裂纹，在交变应力的反复作用下裂纹不断扩展，摇臂有效截面不断减小，当截面削弱到一定程度时，在一个偶然的震动和冲击下，摇臂突然断裂，如图2所示[6]。

图2 摇臂断裂图Fig.2 The fracture of the arm

2 仿真分析

为了深入研究摇臂断裂的原因，使用SolidWorks Simulation软件对摇臂进行受力分析，具体操作步骤依次为：创建算例、应用材料、添加约束、施加载荷、划分网格、运行计算、分析结果。摇臂材料为灰铸铁，抗拉强度为151 MPa，抗压强度为572 MPa。摇臂与鳍轴的连接方式为键连接，所以应添加的约束为键槽两侧面的固定约束及轴孔的固定铰接约束，如图3中箭头①所示。减摇鳍的驱动力来自于与摇臂2个耳环铰接在一起的2个单出杆液压缸，2个液压缸进出油口交叉连接在一起，工作时2缸出力组成力偶(即1个为推力，另1个为拉力)。由于液压缸的系统压力p=10 MPa，缸体内径D=80 mm，活塞杆直径d=55 mm，则单缸可输出的最大推力F1和最大拉力F2为：

将F1和F2添加到摇臂的2个耳环上，如图3中箭头②所示(其中F1方向向下，F2方向向上)，此时摇臂可输出最大扭矩，且摇臂的受力情况也最为恶劣。载荷添加完成后，对摇臂模型划分网格后即可运行计算，摇臂的有限元模型如图3所示。

图3 摇臂有限元分析模型Fig.3 The finite element model of the arm

2.1 应力分析

计算得到的摇臂应力分布如图4所示，可见应力较大的位置为2个耳环根部截面突变处，这与摇臂的实际断裂位置保持一致。由于推力F1大于拉力F2， 受F1作用的耳环根部应力大于受F2作用的耳环根部应力，但实际工作中2个耳环工况相同，都会周期性的受到推力和拉力作用，本算例是输出最大扭矩的特定工况。图5为受F1作用的耳环根部截面突变处左右两侧的应力曲线，两侧应力曲线趋势一致，但由于耳环根部结构的非对称性，右侧应力始终大于左侧。最大应力出现在受F1作用的耳环下方右侧位置，该位置受压，应力大小为266.1 MPa；耳环右侧上方应力大小为220 MPa，该位置受拉。

图6为摇臂安全系数分布图，安全系数定义为材料失效应力与设计应力的比值。由于铸铁属脆性材料，当所受应力大于其强度极限即发生断裂，故失效应力即为其强度极限。安全系数较小的位置为2个耳环根部截面突变处，最小安全系数0.68(安全系数小于1意味着该处应力已超过材料强度极限)出现在受到推力F1作用的耳环上方右侧位置，与最大应力出现位置不一致，这是因为摇臂耳环在推力F1的作用下，其上部受拉，下部受压，而摇臂的抗拉强度远小于抗压强度，故在上下应力相差不多的情况下，耳环上方安全系数小，易发生断裂。从图2中摇臂断口端面的锈蚀情况可以看出断裂是从耳环的上方开始逐渐扩展到下方的，而仿真计算得到的耳环上方安全系数也为最小，可见仿真结果与实际情况符合较好，具有较高的正确性、可靠性。

图4 摇臂Von Mises应力分布Fig.4 The Von Mises stress of the arm

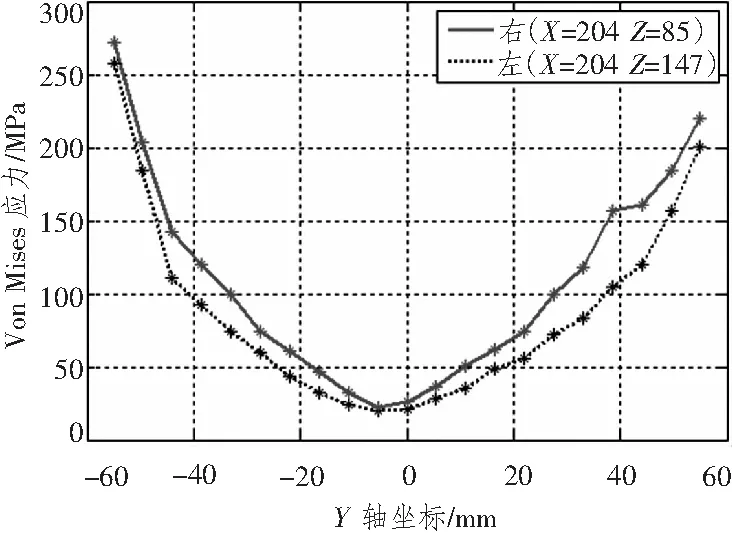
图5 摇臂耳环根部应力曲线Fig.5 The stress curve of the earring root of the arm

图6 摇臂安全系数分布Fig.6 The safety coefficient of the arm

2.2 疲劳分析

图7摇臂疲劳寿命分布图是通过在摇臂2个耳环上施加周期性的推力F1和拉力F2仿真计算得到的。由图7可知，2个耳环根部疲劳寿命较短，是疲劳断裂最易发生的危险区域；耳环与摇臂轴毂相接的位置疲劳寿命最短(为612个交变周期)，这意味着疲劳裂纹将首先发生该位置，随后扩展开来。仔细观察摇臂的断口位置及锈蚀程度，可知裂纹首先出现在靠近摇臂轴毂位置，随后斜向下扩展到耳环根部，最终断裂，这也充分验证了仿真结果的准确性。

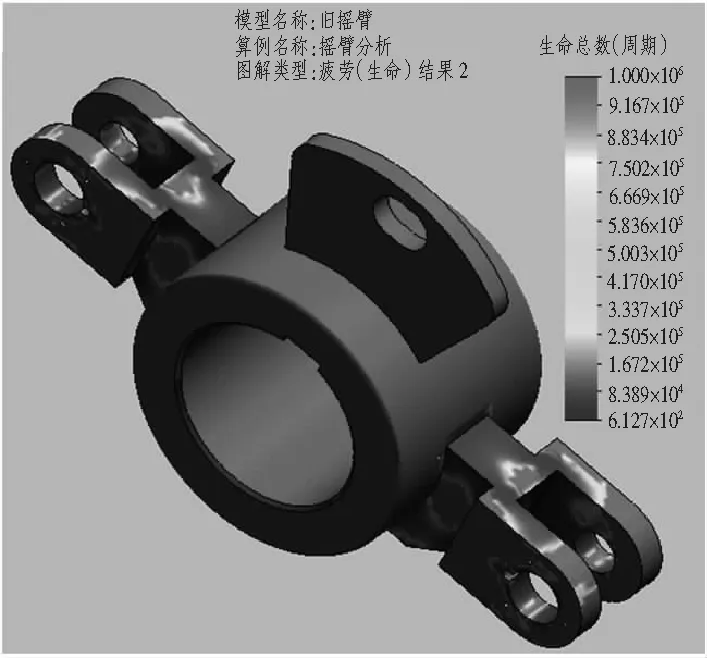
图7 摇臂疲劳寿命分布Fig.7 The fatigue life of the arm

3 优 化

通过上述分析可知摇臂的耳环根部及耳环与轴毂相接位置由于存在结构上的突变，应力容易集中，易发生断裂，是摇臂的薄弱环节。为了避免断裂故障的发生，需对上述位置进行加强，加强的方法即消除耳环与轴毂之间的结构突变，耳环根部直接与轴毂相连。

在相同的工况下对新摇臂进行仿真计算，新摇臂的应力分布情况如图8所示，摇臂耳环应力分布较为均匀，最大应力为134.3 MPa，小于摇臂材料的抗拉、抗压强度。安全系数分布如图9所示，摇臂最小安全系数为1.2(大于1)，说明新摇臂各处应力皆小于材料失效应力，不易发生断裂，零件安全。图10为新摇臂疲劳寿命分布图，最短疲劳寿命为4 780个交变周期，远大于旧摇臂最短疲劳寿命。通过仿真分析可知新摇臂可以在输出最大扭矩情况下正常工作，不发生断裂故障；实船减摇鳍设备替换上新摇臂后，经过长期实行检验，新摇臂工作正常，未出现类似故障，也验证了上述优化方法的有效性。

图8 新摇臂Von Mises应力分布Fig.8 The Von Mises stress of the new arm

图9 新摇臂安全系数分布Fig.9 The safety coefficient of the new arm

图10 新摇臂疲劳寿命分布Fig.10 The fatigue life of the new arm

4 结 语

通过理论分析及仿真计算，对摇臂受力进行分析，确定了摇臂薄弱位置及断裂原因，旧摇臂耳环

根部由于存在结构突变，导致应力集中，最终导致疲劳断裂。结合仿真结果，对摇臂薄弱环节进行加强优化，并对优化后的新摇臂进行仿真分析，结果表明新摇臂安全系数分布均匀，整体可靠性较高，且经过长期试验验证其工作良好，明显优于旧摇臂，也验证了仿真优化方法的正确性及有效性。

[1] 沈余生.减摇鳍机械装置设计相关分析[J].船舶工程，2009(2)：30-31.

SHEN Yu-sheng.Correlation analysis of machine design of stabilizing fin[J].Ship Engineering,2009(2):30-31.

[2] 曾晓华，金全，彭利坤.某船减摇鳍摇臂断裂故障分析[J].中国修船，2013，26(5)：22-23.

ZENG Xiao-hua,JIN Quan,PENG Li-kun.Fracture failure analysis of the rocker arm of fin stabilizer[J].China Shiprepair,2013,26(5):22-23.

[3] 刘天鹏.受压状态下脆性材料断裂机理的试验研究[D].西安：西安理工大学，2006.

LIU Tian-peng.Test research on the fracture mechanics for the brittle materials under compressing[D].Xi′an:Xi′an University of Technology,2006.

[4] 李智慧，师俊平，汤安民.金属材料脆性断裂机理的实验研究[J].应用力学学报，2012，29(1)：48-53.

LI Zhi-hui,SHI Jun-ping,TANG An-min.Experimental research on the brittle fracture mechanism in metal material[J].Chinese Journal of Applied Mechanics,2012,29(1):48-53.

[5] 郭大展，胡志忠，安仁杰，等.球墨铸铁疲劳裂纹的发生和发展[J].西安交通大学学报，1981，15(6)：51-60.

GUO Da-zhan,HU Zhi-zhong,AN Ren-jie,et al.Fatigue crack initiation and propagation in nodular cast iron[J].Journal of Xi’an Jiaotong University,1981,15(6):51-60.

[6] 曹睿，任学冲，陈剑虹.铸铁断裂机理原位拉伸研究[J].甘肃工业大学学报，2003，29(3)：8-13.

CAO Rui,REN Xue-chong,CHEN Jian-hong.Investigation of fracture mechanisms of cast iron by means of situ observation[J].Journal of Gansu University of Technology,2003,29(3):8-13.