鱼雷楔环连接结构等效刚度建模与模态分析

马锐磊，尹韶平，曹小娟，严 海，徐新栋

(1.中国船舶重工集团公司 第705研究所，陕西 西安 710075； 2.水下信息与控制重点实验室，陕西 西安 710075)

0 引 言

鱼雷是一种涉及机械、电子、力学、动力、控制、水声、爆炸等多学科的高技术水下精确制导武器。为了满足生产、加工、调试、安装、维修使用和保障等方面的要求，对鱼雷进行必要的分段。进行鱼雷舱段间的连接设计时必须在满足强度、刚度和密封要求的前提下，做到拆装使用方便，并尽量保证雷体表面的光顺，提高保障性并对鱼雷水下运动不产生不利影响。鱼雷舱段连接方式主要有螺钉式连接、卡箍连接和楔环连接等几种方式。其中楔环连接结构具有雷体表面光顺、占用壳体内部空间小、结构尺寸紧凑，质量轻、连接可靠、壳体受力均匀等优点[1]，是目前常用的连接方式之一。

楔环连接结构动力学特性复杂，对鱼雷结构动力学特性影响较大。在进行鱼雷结构分析时，如何合理对楔环连接结构进行简化，是建立有限元模型关键，直接影响到结构动力学性能分析的精度。传统处理方式主要分为2种思路：第1种是连续化方法，即将楔环连接结构连同连接壳体拆分为较简单的几部分，设置楔环连接处的刚度与壳体一致。文献[2]将楔环连接壳体看成由弹性圆环、短圆柱形壳及长圆柱形壳组成，并进行载荷分析；文献[3]和文献[4]将楔环连接结构简化为外环、楔带、内环的结构，其中文献[4]应用Ansys软件对楔环连接壳体结构进行模态分析和谱分析，仿真与试验对比曲线在600～1 200 Hz频段出现2个波峰，与试验数据有明显差别，可能是建模时将楔环连接处设置为刚性连接，使得连接处刚度增加，导致仿真结果与试验数据在共振峰处有较大差异。第2种思路是静力学和动力学联合计算分析，通过设置时间步，先对每一时间步进行静力学分析，然后将计算得到的静力学刚度矩阵代入动力学进行分析计算。这种分析方法涉及复杂的非线性接触关系解算并且耗费时间，与试验对比计算相对误差在10%左右。

本文针对传统楔环处理方式存在分析精度较低以及分析计算复杂的问题，提出一种鱼雷楔环连接结构有限元建模方法——等效刚度法，通过将楔环连接结构简化为2个等效壳体和1个等效楔环结构，根据固有频率的试验数据，以等效楔环结构的弹性模量E为优化变量，运用Nastran sol200模块对模型进行优化，优化后模型的仿真计算相对误差在4%以内，模态振型与试验数据基本一致，说明采用等效刚度法建立模型并运用Nastran sol200模块进行模型优化的模态分析过程较以往分析方法具有更简单的模型、更高的建模效率及仿真精度。

1 模态理论及等效方法

1.1 模态分析理论

结构系统模态分析的核心内容，就是通过计算或试验的方法，确定用来描述结构系统特性的固有频率、阻尼比和振型等模态参数[5-7]。在数学上，就是求解结构动力学方程的特征值或广义特征值的问题。结构系统的动力学方程通常可以表示为：

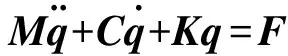
(1)

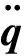
略去结构系统的运动微分方程中的阻尼力项和外载荷项，得到系统无阻尼自由振动的动力学方程：

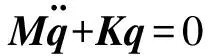
(2)

令式(2)的解为

q=Asin(ωt+φ)，

(3)

式中：A为振幅，由初始条件决定；φ为相位角，由初始条件决定；ω为固有频率，由系统固有特性决定。

代入式(2)可得

(K-ω2M)Asin(ωt+φ)=0，

(4)

由于A≠0，有

|K-ω2M|=0，

(5)

由固有频率求解表达式ω2=K/M可知：固有频率与模型质量M和模型刚度K有关，对于本文所建连接壳体模型，质量均按实际情况加载，因此模型刚度K成为唯一影响因素。根据材料力学相关理论，模型刚度K为材料弹性模量E以及模型相关形状参数的函数，即K=Ef(l,h,r)(其中l,h,r为模型形状参数)，本文模型按照实际尺寸建立，故最终固有频率的求解只与材料弹性模量E相关。

1.2 楔环连接结构等效方法

鱼雷壳体楔环式连接方式(如图1所示)是利用2个带楔形面的开口圆环(楔环1和楔环2)在周向相对运动时产生轴向的拉力将鱼雷2个舱段壳体连接在一体。楔环安装在2个舱段壳体形成的矩形环槽内，在雷体表面只留有1个紧密配合的接缝和一个楔环安装窗口。

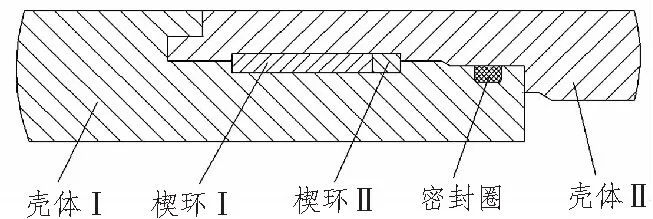
图1 鱼雷壳体楔环式连接示意图Fig.1 Wedged-ring connection structure

由于楔环连接结构复杂，有限元建模时需要进行必要的简化，通常简化后的模型依然存在诸多接触面、空腔等特征，使得在后续分析计算时接触关系的确定、受力情况的分析变得困难，影响计算的收敛性和稳定性。针对这种情况，本文提出一种楔环连接结构的等效模型，考虑到后续模态计算分析的需要，将楔环Ⅰ、楔环Ⅱ、密封圈以及壳体I和壳体II的一部分等效为一个整体，如图2所示。模型等效后，将楔环连接处从与壳体连接状态下分离出来，模态分析时对楔环连接处赋予等效弹性模量E，便于后续模型优化，从而提高有限元计算的精度。

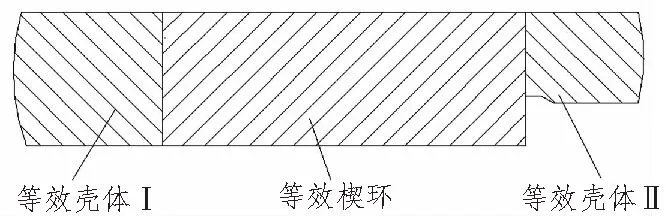
图2 鱼雷楔环连接结构等效示意图Fig.2 Equivalent wedged-ring connection structure

2 有限元建模与计算

2.1 有限元建模

鱼雷壳体楔环部位涉及到2段壳体、2个楔环、填片、盖板和盖板螺钉等多个零件，考虑到填片、盖板和盖板螺钉基本上不起传递承受载荷，分析时主要以楔环和壳体为对象进行建模，同时，忽略壳体上盖板螺钉孔、楔环槽的倒角等对后续分析计算结果几乎没有影响的微小特征。

在利用Hypermesh进行网格划分时，充分考虑网格质量对计算的收敛性、计算精度和计算时间等的影响，首先以几何模型为基础力求选择最合适的单元类型，根据各部分结构的特点，灵活使用六面体、五面体等网格单元；其次，网格划分时，注意2段壳体之间周向网格数量的一致性，保证连接处网格单元的紧密连接和平滑过渡，在满足计算精度的条件下，控制网格数量，选择适当的网格密度，从而节约计算时间。其中鱼雷舱段连接模型如图3所示，楔环与壳体连接状态下的模型局部视图如图4所示。

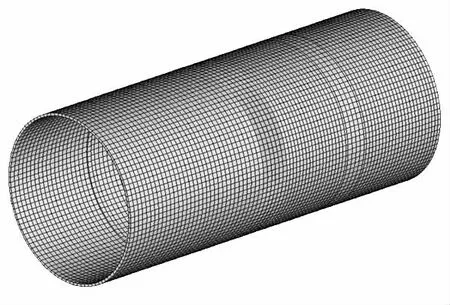
图3 鱼雷舱段连接模型Fig.3 Connection structure

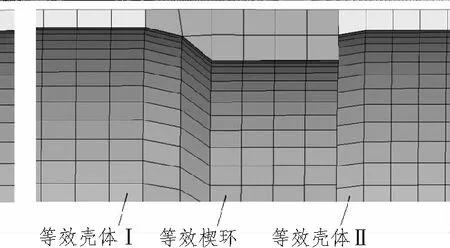
图4 连接状态局部视图Fig.4 Part of structure

2.2 模型优化

结构有限元分析模型计算的结构响应与实测响应之间不可避免地存在一定偏差，误差产生的主要来源有：1)由于结构有限元分析模型是按照设计图样中公称尺寸构造的，同时还包含有理想化假定或简化，例如忽略了盖板螺钉孔、楔环槽的倒角、零件间间隙等，与结构实际的状况存在差异；2)在分析时，材料的密度、弹性模量、泊松比等参数均按材料设计手册中数值选取，而实际材料的特性和手册上规定的数值势必有一定差异，因制造及使用环境的变化也会给这些参数带来一定的误差；3)计算时进行的有限元离散化等处理也会引入误差。在利用所建模型进行分析时，必须采取一定的方法进行优化来减小分析模型与结构实际响应之间的误差[8-10]。

本文应用Nastran sol200模块对有限元模型进行优化。考虑到鱼雷舱段楔环连接处的刚度和非连接处相比有所减小，即等效楔环处的弹性模量小于壳体或楔环材料的弹性模量，因此把等效楔环处的弹性模量E作为优化设计变量，并对其设置变动范围，初始值取E=40 GPa、浮动下限取E=20 GPa、浮动上限取E=50 GPa、步长设置为1 GPa；按照壳体楔环连接模型固有频率与试验数据的差值最小为目标；基于实验数据，设置约束条件为模型第2、3阶固有频率，第2阶固有频率约束范围为200-300 Hz；第3阶固有频率约束范围为400～500 Hz。

2.3 计算结果

模型未经优化时，选取等效壳体1，等效壳体2与等效楔环的材料性能如下：弹性模量E=71 GPa，泊松比ν=0.33，密度ρ=2 700 kg/m3。用所建模型，利用Nastran进行模态计算，其1阶、2阶、3阶及4阶模态的固有频率分别为192.41 Hz，270.28 Hz，456.96 Hz和782.69 Hz。

按照2.2中的优化设置，利用Nastran sol200模块优化后，其1阶、2阶、3阶及4阶模态的固有频率分别为173.52 Hz，251.07 Hz，437.92 Hz，776.68 Hz。

2.4 与试验结果对比

为验证模型优化的精确度，进行壳体楔环处模态试验，模型修正前后有限元计算结果与试验数据结果对比情况见表1。

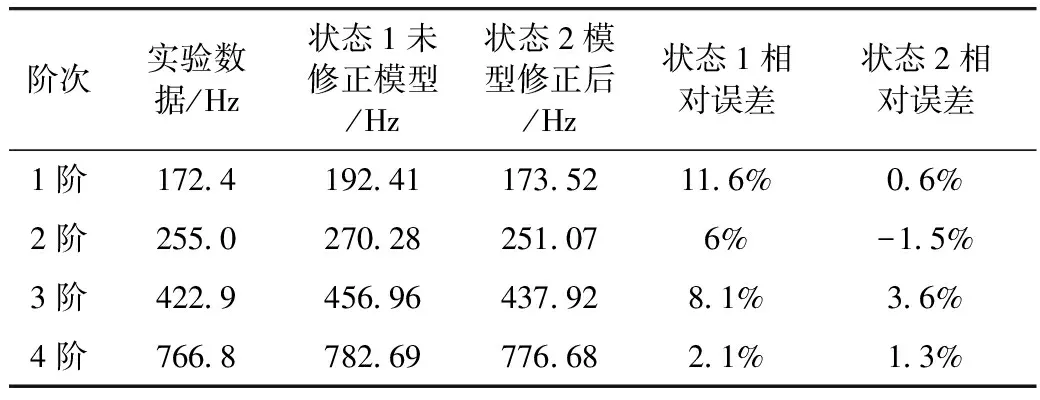
表1 试验与仿真结果对比

从表1中可以看出，优化后的固有频率值较优化前的值更接近试验数据，相对误差较小。但是，单纯以计算值与实验值绝对差值最小为目标函数的优化结果并不能说明有限元分析结果的准确性，还必须保证其模态振型与试验振型的一致性。试验模态振型与优化后计算模态振型比较见图5～图12。

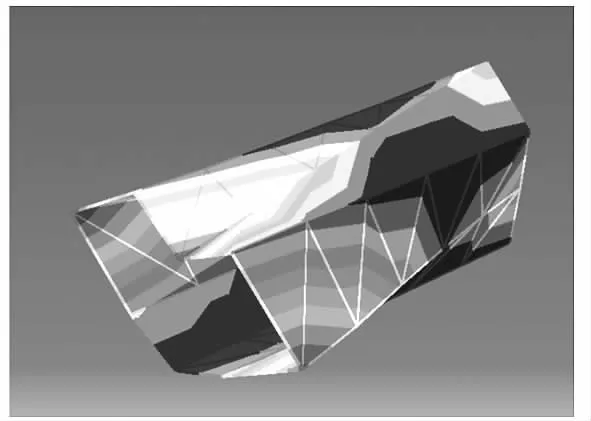
图5 试验第1阶振型Fig.5 The first-order modal vibration mode of testing

图6 计算第1阶振型Fig.6 The first-order modal

图7 试验第2阶振型Fig.7 The second-order modal vibration mode of testing

图8 计算第2阶振型Fig.8 The second-order modal vibration mode of simulation

图9 试验第3阶振型Fig.9 The third-order modal vibration mode of testing

图10 计算第3阶振型Fig.10 The third-order modal vibration mode of simulation

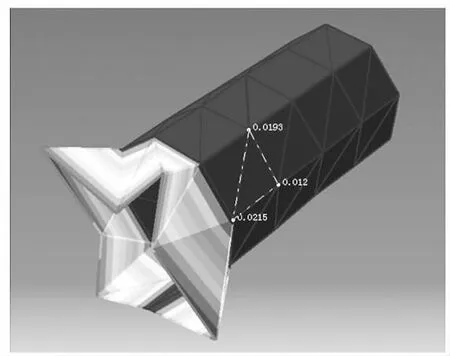
图11 试验第4阶振型Fig.11 The fourth-order modal vibration mode of testing

图12 计算第4阶振型Fig.12 The fourth-order modal vibration mode of simulation

将有限元仿真获得的模态振型与试验结果对比，可以看出：

1)二者的第1阶模态振型均为两端面产生椭圆形变形，且两端变形方向相互垂直；

2)二者的第2阶模态振型均为右端面产生椭圆形变形，左端面形状不变；

3)二者的第3阶模态振型均为左端面产生三角形变形，右端面形状不变；

4)二者的第4阶模态振型均为左端面产生四角形变形，右端面形状不变。

3 结 语

本文针对鱼雷壳体连接结构模态分析时，楔环连接处刚度处理不妥造成模态计算精度较低的问题，提出楔环连接处等效刚度的处理方法，并运用Nastran sol200模块对等效模型进行优化。与实验结果的对比表明：计算的固有频率和模态振型与试验结果吻合度较优化前有了较大提高，误差在4%以内。提出的楔环连接结构有限元建模方法简单有效，可推广至全雷有限元分析中。

[1] 尹韶平，刘瑞生.鱼雷总体技术[M].北京：国防工业出版社，2011.

[2] 黄鹏，莫军，尹益辉，等.拉伸载荷下楔环连接壳体的应力解析方法[J].工程力学，2007，24(8):66-71.

HUANG Peng，MO Jun，YIN Yi-hui，et al.Analytic solution for stress in wedged-ring connected shell under tensile loading[J].Engineering Mechanics，2007，24(8):66-71.

[3] 刘曜，鲍挺俊，马震宇.薄壁圆筒楔环连接结构承载能力研究[J].机械设计与制造，2009(2)：140-142.

LIU Yao，BAO Ting-jun，MA Zhen-yu. The research on the load bearing capacity of wedged-ring joint structure of thin-wall cylinder[J].Machinery Design and Manufacture，2009(2)：140-142.

[4] 刘飞飞，石秀华，杜喜昭，等.楔环联接方式的圆柱壳体振动传递特性分析[J].理论与方法，2011，30(12)：30-33.

LIU Fei-fei，SHI Xiu-hua，DU Xi-zhao，et al.Analysis on the vibration transfer characteristic of the cylindrical shell with wedge ring[J]. Theory and Method，2011，30(12)：30-33.

[5] 姚熊亮.结构动力学[M].哈尔滨：哈尔滨工程大学出版社,2007.

[6] 曹银萍，石秀华.基于ANSYS的鱼雷有限元建模与模态分析[J].弹箭与制导学报，2009，29(3)：289-292.

CAO Yin-ping，SHI Xiu-hua.Finite element modeling and modal analysis of torpedo based on Ansys[J].Journal of Projectiles,Rockets,Missiles and Guidance，2009，29(3)：289-292.

[7] 梁跃，何长富，彭博.鱼雷热动力发动机机体振动模态分析[J].鱼雷技术，2005，13(4)：17-20.

LIANG Yue，HE Chang-fu，PENG Bo.Structural vibration modal analysis of torpedo thermal power engine[J].Torpedo Technology，2005，13(4)：17-20.

[8] 刘荣贺，姜虹，于开平，等.基于Nastran优化的某导弹结构模型修正[J].现代防御技术，2011，39(6)：106-110.

LIU Rong-he，JIANG Hong，YU Kai-ping，et al.Missile structure model updating based on nastran optimization[J].Modern Defence Technology，2011，39(6)：106-110.

[9] 李增刚.Nastran快速入门与实例[M].北京：国防工业出版社，2007.

[10] 隋允康，杜家政，彭细荣.MSC.Nastran有限元动力分析与优化设计实用教程[M].北京：科学出版社，2004.