视频监控图像的运动模糊方向估计

吴海滨，刘 超，于晓洋，孙晓明，胡丽娟

(哈尔滨理工大学 测控技术与仪器黑龙江省高校重点实验室，黑龙江 哈尔滨 150080)

1 引 言

视频监控已成为安防领域的重要手段之一，监控视频中单帧图像的清晰度决定了后续信息提取的准确度。线性运动模糊是视频监控中最典型的模糊类型，这是由摄像机的视场角和监控目标的行为方式共同决定的。摄像机和监控目标之间的相对运动可由线性运动模糊模型表示，其研究对于视频监控图像模糊复原具有普遍意义。

线性运动模糊模型中，模糊参数包括模糊尺度L和模糊方向θ，尤以后者对模糊复原效果起决定作用且易受干扰难以准确估计。国内外相关研究较多，Yitzhaky等[1]采用2×2的微分算子仅在模糊方向为0°～45°范围内获得较准确的估计结果；在此基础上，陈前荣等[2]采用3×3的微分算子结合双线性插值提高了估计准确度。谢伟等[3-4]采用求模糊图像倒频谱及分析谱上特征点的方法估计模糊参数，方法简单有效但对噪声敏感。Moghaddam等[5-6]在模糊图像傅里叶频谱中采用 Radon 变换估计模糊方向，对于较大模糊方向获得高准确度，但该方法受图像自身结构影响较大。乐翔等[7]针对模糊图像频谱中央十字亮线的特性，采用频谱分块的方法有效避免了该亮线的干扰，但该方法对中央亮线宽度的准确性要求较高。Sun等[8]在模糊图像梯度域中利用归一化的Radon变换估计模糊方向，准确度较高但只适用于等宽高比图像。李宇成等[9-11]给出模糊参数与图像高宽比的关系，适用于任意高宽比图像且抗噪能力强，但未考虑实际频谱中央十字亮线的干扰。Monhammadi等[12]研究了模糊参数与车辆速度间的关系，利用Radon变换得到模糊参数，实现了车辆速度检测，是模糊图像复原的一种重要实际应用。

综上，对于任意高宽比模糊图像，针对傅里叶频谱中央十字亮线干扰问题，本文给出频谱子块候选原则，在候选子块中利用归一化radon变换估计模糊方向。最后，实验对比本文方法与现有典型方法的模糊方向估计准确度。

2 Radon变换模糊方向估计方法分析

线性运动模糊图像g(x,y)可由式(1)表述：

g(x,y)=f(x,y)⊗h(x,y)+n(x,y)，

(1)

式中：f(x,y)为监控目标的原始光强，h(x,y)为成像系统函数，n(x,y)为高斯白噪声。

根据线性运动模糊特性，h(x,y)可由式(2)表述，式中L为模糊尺度，θ为模糊方向。

(2)

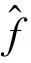
G(u,v)=F(u,v)·H(u,v)+N(u,v).

(3)

若摄像机与监控目标以水平速度a/T，垂直速度b/T相对运动，则频域中成像系统函数H(u,v)可由式(4)表述，式中M、N分别为图像行数和列数，a、b分别为水平位移和垂直位移，T为运动时间。

(4)

二维Radon变换定义为函数g(x,y)在角度为θ、距原点为ρ的直线上的投影，如式(5)所示。

(5)

式中:δ为冲激函数，它确保该变换沿着直线ρ-xcosθ-ysin θ=0对g(x,y)积分；θ的取值范围为[0°, 180°]。(ρ,θ)平面上的每一点对应xoy平面上的一条直线，则g(x,y)平面上直线的检测转化为(ρ,θ)平面上亮、暗点的检测，最终形成一条模糊方向估计曲线。

Radon变换可计算图像矩阵沿特定方向的投影，而其频谱图中平行直线方向上积分会出现峰值，该峰值所对应的角度与图像发生运动模糊的方向满足式(5)关系。

视频监控图像多为高宽不等图像。图1给出了两幅不同高宽比模糊图像的频谱图和模糊方向估计曲线。两幅图像高宽分别为512 pixel×512 pixel和576 pixel×720 pixel像素，模糊方向均为45°。

图1 Radon变换模糊方向估计

由图1可知，采用Radon变换根据频谱图估计模糊方向时，存在以下问题：

(1)如图1(c)和(d)所示，频谱图中存在十字形的亮线，其形成原因是原始光强图像是非周期性的，它与成像系统函数进行非完全卷积时发生“边缘截断效应”。该十字亮线将频谱图分割成2个或4个子块，导致频谱图的Radon变换在0°(180°)、90°方向形成干扰，产生错误估计。

(2) 由Radon变换的定义，变量ρ与图像对角线的长度正相关，沿对角线方向投影的像素点个数最多。对于等高宽比图像，这导致0°～180°范围内45°(135°)方向上的积分值偏大，影响模糊方向估计，称之为“对角线干扰”；对于不等高宽比图像，在其对角线附近(接近45°、135°)存在类似干扰。

(3) 等高宽比图像的频谱图中，模糊方向估计曲线在对角线(45°和135°)方向达到极大值，其对角线与运动方向垂直；不等高宽比图像的频谱图中，模糊方向估计曲线的极大值仍在对角线处，但偏离45°和135°，其对角线并不与运动方向垂直。因此，当图像高宽比不等时，模糊方向估计曲线的极大值与模糊方向并不垂直，需建立二者转换关系。

本文将针对上述问题加以改进，给出综合解决方法。

3 改进的分块Radon变换模糊方向估计方法

如前所述，十字亮线干扰、对角线干扰对运动模糊方向估计有较大影响。为充分利用频谱图中明暗相间的平行条纹和十字亮线所处的特殊位置，可将频谱图分块[13]，并按一定的原则选择合适的子块进行Radon变换。具体步骤如下：

(1)细化分块，十字亮线将图像频谱分成4个等明(暗)条纹数目的子块，定义子块条纹密度为σi=sn/min(h,w)，式中sn为条纹数量，h和w分别为子块的高和宽，i为子块序数。在子块中选择最大的σi，若其大于整幅频谱图像的σ值，则继续细分。

(2)将Radon变换结果归一化，如式(6)，降低Radon变换对对角线干扰的敏感度。

Rnorm(ρ,θ)=

(6)

式中：Rnorm为归一化结果，Ones为全1矩阵。

(3)修正频谱图中条纹倾斜角度与模糊方向的偏差，如式(7)，对于任意高宽比，均可准确估计模糊方向。

(7)

式中：φ为频谱条纹的倾斜角。由式可知，若条纹倾斜角已知，模糊方向的估计误差与高宽比直接相关；当M=N时，条纹的倾斜角与模糊方向角相互垂直。

图2给出了模糊方向为60°的Lena频谱图像及归一化前后的Radon变换模糊方向估计曲线。

比较图2(b)和图2(c)可知，归一化后的Radon变换模糊方向估计曲线中45°(135°)附近的对角线极值干扰受到有效抑制，有助于提高模糊方向估计的准确性。

4 模糊方向估计实验

图3为75°方向Lena模糊图像的模糊方向估计实验，图3(a)为整图频谱图，图3(b)为子块频谱图。由实验结果可知，经典Radon变换估计的模糊方向受十字亮线干扰和对角线干扰严重，在0°、90°、45°(135°)处出现干扰峰值。子块Radon变换在一定程度上降低了两类干扰；由图3(e)可知，归一化后两类干扰被有效抑制。

图3 模糊方向估计实验Fig.3 Blurred direction estimation experiments

模糊方向估计实验数据如表1、表2所示。

表1 Lena 模糊方向估计数据

表2 Barbara模糊方向估计数据

由表中数据可知，由于经典Radon变换受十字亮线干扰和对角线干扰严重，因此出现多个错误估计结果，导致较大误差。与经典Radon变换相比，本文改进方法在非对角线的方向如60°、75°、105°、120°、150°等处能较准确地估计模糊方向。对应表中数据的误差曲线如图4所示。

图4 方向估计误差比较Fig.4 Error comparison of direction estimation

5 结 论

模糊方向θ的估计准确度直接影响模糊图像复原效果。在经典Radon变换的基础上，本文通过频谱图细化分块、Radon变换归一化和修正频谱图中条纹倾斜角度与模糊方向的偏差等方法，提出一种改进的运动模糊方向估计方法。实验结果表明，相对经典Radon变换估计方法，本文方法能有效抑制十字亮线干扰和对角线干扰，避免模糊方向估计曲线在0°、90°、45°(135°)处出现干扰峰值，在非对角线的方向如60°、75°、105°、120°、150°等处能较准确地估计模糊方向，误差约4～6°，稳定性明显提高，且适用于任意高宽比图像。

今后工作将着重研究摄像机与监控目标在复杂相对运动下产生的非均一性模糊复原方法。

[1] Yitzhaky Y, Kopeika N S. Identification of blur parameters from motion blurred images [J].GraphicalModelsandImageProcessing, 1997, 59(5): 310-320.

[2] 陈前荣，陆启生，成礼智. 运动模糊图像的运动模糊方向鉴别[J]. 国防科技大学学报，2004(1)：41-45.

Chen Q R, Lu Q S, Chen L Z. Identification of the motion blurred direction of motion blurred images [J].JournalofNationalUniversityofDefenseTechnology, 2004(1): 41-45. (in Chinese)

[3] 谢伟，秦前清. 基于倒频谱的运动模糊图像 PSF 参数估计[J]. 武汉大学学报，2008，33(2)：128-131.

Xie W, Qin Q Q. Estimating blur parameters of point spread function of motion-blurred image based on Cepstrum [J].GeomaticsandInformationScienceofWuhanUniversity, 2008, 33(2): 128-131. (in Chinese)

[4] 石明珠，许廷发，张坤. 运动成像混合模糊的全变分图像复原[J]. 光学 精密工程，2011，19(8)：1973-1981.

Shi M Z, Xu Y F, Zhang K. Total variation image restoration for mixed blur in moving image [J].Opt.PrecisionEng., 2011, 19(8): 1973-1981. (in Chinese)

[5] Moghaddam M E, Jamzad M. Finding point spread function of motion blur using Radon transform and modeling the motion length [C].IEEE4thInternationalSymposiumonSignalProcessingandInformationTechnology, 2004: 314-317.

[6] 孙辉. 相位相关技术实现离焦模糊图像运动估计[J]. 液晶与显示, 2012, 27(2)：223-228.

Sun H. Estimation of displacement for out-of-focus blurred image using phase-only correlation [J].ChineseJournalofLiquidCrystalsandDisplays, 2012, 27(2): 223-228. (in Chinese)

[7] 乐翔，程建，李民. 一种改进的基于Radon变换的运动模糊图像参数估计方法[J]. 红外与激光工程, 2011, 40(5)： 963-969.

Le X, Cheng J, Li M. Improved approach to motion blur identification based on Radon transform [J].InfraredandLaserEngineering, 2011, 40(5): 963-969. (in Chinese)

[8] Sun H W, Desvignes M, Yan Y H,etal. Motion blur parameters identification from Radon transform image gradients [C]. 35thAnnualConferenceoftheIEEEIndustrialElectronicsSociety, 2009: 2098-2103.

[9] 李宇成，贾宝华，杨光明. 运动模糊图像的参数估计与恢复[J]. 计算机工程与设计, 2010, 31(19)：4247-4249.

Li Y C, Jia B H, Yang G M. Blur parameter identification and restoration of motion blurred image [J].ComputerEngineeringandDesign, 2010, 31(19): 4247-4249. (in Chinese)

[10] Phansalkar N. Determination of linear motion point spread function using Hough transform for image restoration [C].ComputationalIntelligenceandComputingResearch,Communication,Networking&Broadcasting, 2010: 1-4.

[11] 朱明，杨航，贺柏根，等. 联合梯度预测与导引滤波的图像运动模糊复原[J]. 中国光学, 2013, 6(6)：850-854.

Zhu M, Yang H, He B G,etal. Image motion blurring restoration of joint gradient prediction and guided filter [J].ChineseOptics, 2010, 31(19): 4247-4249. (in Chinese)

[12] Javad M, Rohollah A, Haghighat M K. Vehicle speed estimation based on the image motion blur using Radon transform [C]. 2ndInternationalConferencesonAnalysisandSignalProcessingSystem, 2010: 243-247.

[13] 刘翔，周桢. 基于分块背景建模的运动目标检测技术[J]. 液晶与显示, 2011, 26(6)：831-835.

Liu X, Zhou Z. Moving objectives detection technology based on block processing of background model establishment [J].ChineseJournalofLiquidCrystalsandDisplays, 2011, 26(6): 831-835. (in Chinese)