一道中考模拟题的推广

☉湖南省慈利一鸣中学 满 群

一道中考模拟题的推广

☉湖南省慈利一鸣中学 满 群

“全等与相似”作为空间与图形体系中重要的一部分内容，是中考的一个热点，也是一个难点，近些年来，在各省市中考题中都有涉及.解决与图形全等或相似有关的问题，需要掌握基本图形（三角形）全等或相似的概念、条件和性质，同时要学会从一般的几何图形中分离出基本图形，学会在观察与操作活动中，探索基本图形的性质与特征，学会有条理地思考、表达，学会综合利用各种基本图形的性质分析问题，更要注意转化、构造等数学思想方法的运用.在多年的教学过程中，笔者发现将“全等与相似”两者类比研究更相得益彰.

波利亚说过：“类比是一个伟大的引路人”.本文就从南京市2013年中考模拟试卷上的一道“四边形的全等判定”的探究题出发，继而探究一个“四边形的相似判定”变式题，与读者分享交流.

一、原题呈现

【问题提出】

规定：四条边对应相等，四个角对应相等的两个四边形全等.

我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.

【初步思考】

在两个四边形中，我们把“一条边对应相等”或“一个角对应相等”称为一个条件.满足四个条件的两个四边形不一定全等，如边长相等的正方形与菱形就不一定全等.类似地，我们容易知道两个四边形全等至少需要5个条件.

【深入探究】

小莉所在学习小组进行了研究，她们认为5个条件可分为以下四种类型：

（Ⅰ）一条边和四个角对应相等；

（Ⅱ）两条边和三个角对应相等；

（Ⅲ）三条边和两个角对应相等；

（Ⅳ）四条边和一个角对应相等.

（1）小明认为“（Ⅰ）一条边和四个角对应相等”的两个四边形不一定全等，请你举例说明.

（2）小红认为“（Ⅳ）四条边和一个角对应相等”的两个四边形全等，请你结合图形进行证明.

已知：如图1，________________________________.

求证：_________________________.

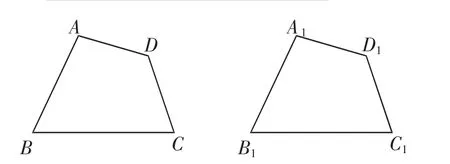
图1

（3）小刚认为还可以对“（Ⅱ）两条边和三个角对应相等”进一步分类，他以四边形ABCD和四边形A1B1C1D1为例，分为以下几类：

其中能判定四边形ABCD和四边形A1B1C1D1全等的是_________（填序号），概括可得“全等四边形的判定方法”，这个判定方法是________________________（用文字叙述）.

（4）小亮经过思考认为也可以对“（Ⅲ）三条边和两个角对应相等”进一步分类，请你仿照小刚的方法先进行分类，再概括得出一个全等四边形的判定方法（用文字叙述）.

解答：（1）如正方形与矩形有一条边对应相等和四个角对应相等，但显然不一定全等.

（2）已知，如图2，在四边形ABCD和四边形A1B1C1D1中，AB＝A1B1，BC＝B1C1，CD＝C1D1，DA＝D1A1，∠B＝∠B1.

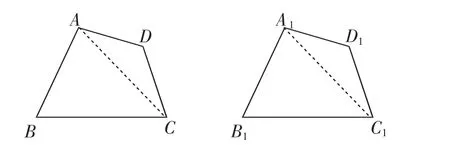
图2

求证：四边形ABCD≌四边形A1B1C1D1.

（3）①②③；有一组邻边和三个角对应相等的两个四边形全等.

（4）分为四类：

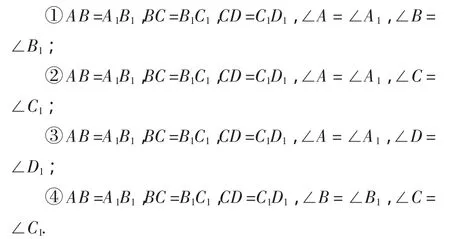
有三条边和这三条边中每一组邻边的夹角对应相等的两个四边形全等.

点评：本题从三角形全等的判定出发，推广到四边形的全等判定.首先题目给出了两个四边形全等至少需要5个条件的结论，接着将5个条件分成了4类：一条边和四个角对应相等、两条边和三个角对应相等、三条边和两个角对应相等、四条边和一个角对应相等，继而针对上述4种分类提出了4个问题，题目由易到难，以基本图形（相似三角形）的知识为载体，渗透并引导学生提炼数学思想方法，从而体会一类问题的本质.

二、变式探究

为了能让学生更加熟练地掌握此类问题的解法，体会全等与相似之间的联系，继而达到学一题会一类的境界，笔者在课堂上将全等和相似结合起来让学生研究，于是在课堂上提出了如下问题.

【问题提出】

我们借助“探索三角形相似的条件”、“探索四边形全等的条件”所获得的经验与方法，可以对“四边形相似的条件”进行探究.

【基本思路】

规定：四条边对应成比例，四个角对应相等的两个四边形相似.在两个四边形中，我们把“一个角对应相等”或“两组边对应成比例”称为一个条件.在探索中发现，满足四条边对应成比例的两个四边形不一定相似，如：四条边对应成比例的正方形与菱形就不一定相似.类似地，四个角对应相等的两个四边形也不一定相似，请你举例说明_________________________.

【初步思考】

在探索中进一步发现，如果两个四边形的四条边对应成比例，再添加一个角对应相等，那么这两个四边形相似.请结合图3进行说明.

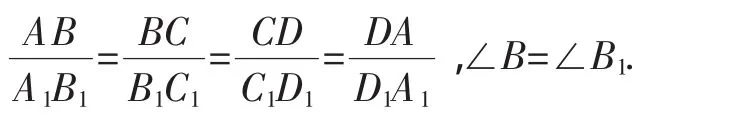
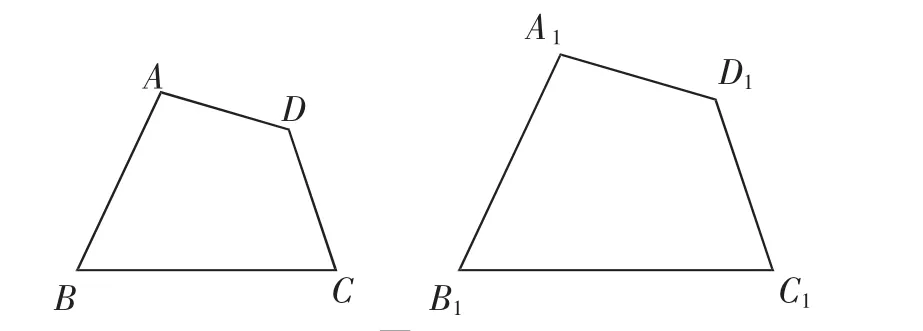
图3

试说明：四边形ABCD∽四边形A1B1C1D1.

【深入探究】

探究可得判定两个四边形相似的条件可分为以下三个类型：

（Ⅰ）四条边对应成比例和一个角对应相等；

（Ⅱ）三条边对应成比例和两个角对应相等；

（Ⅲ）两条边对应成比例和三个角对应相等.

（1）我们对“（Ⅱ）三条边对应成比例和两个角对应相等”进一步分类，以四边形ABCD和四边形A1B1C1D1为例（如图3），分为以下几类：

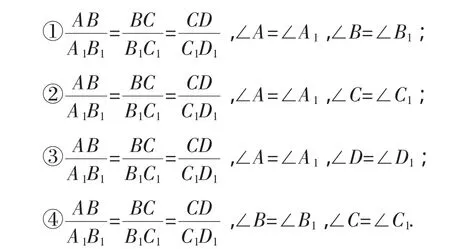
其中能判定四边形ABCD和四边形A1B1C1D1相似的是_________（填序号），概括可得“相似四边形的判定方法”，这个判定方法是________________________（用文字叙述）.

（2）请对“（Ⅲ）两条边对应成比例和三个角对应相等”进一步分类，仿照上述的方法先进行分类，再概括得出一个相似四边形的判定方法（用文字叙述）.

解答：［基本思路］

如：正方形与矩形的四个角对应相等，但它们不一定相似.

【初步思考】

如图4，连接AC、A1C1.

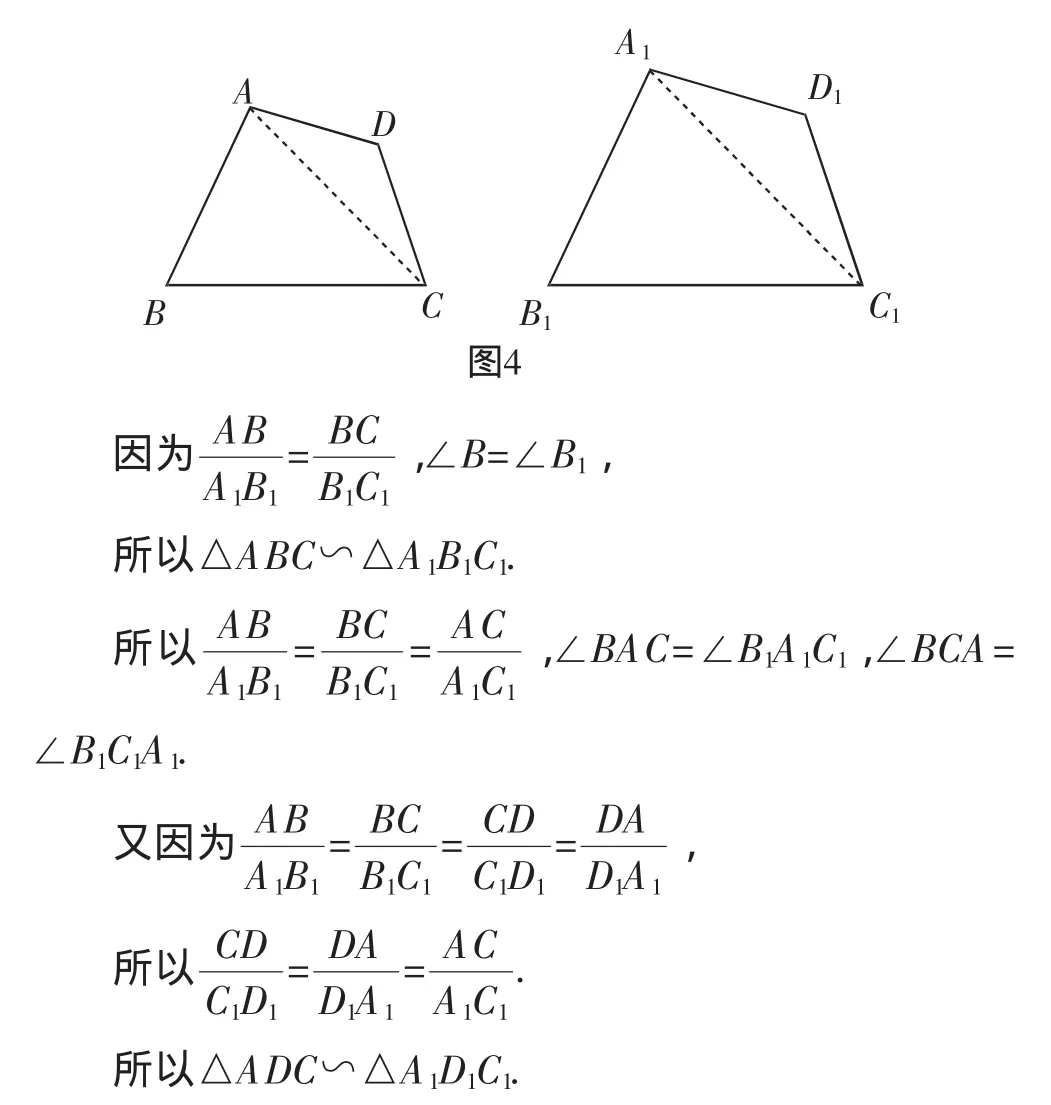
所以四边形ABCD∽四边形A1B1C1D1.

【深入探究】

（1）④；三边对应成比例且三边中的相邻两边的两个夹角对应相等的两个四边形相似.

（2）分为两类：

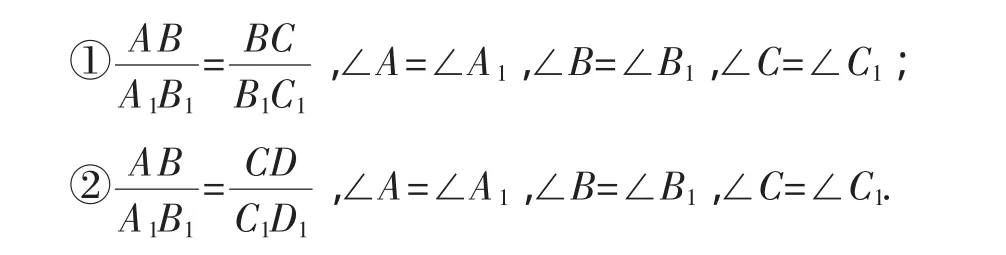
文字叙述：两组邻边对应成比例且三个角对应相等的两个四边形相似.

点评：本题从三角形相似的判定、四边形全等的判定出发，推广到四边形的相似判定.难度相比全等有一定的提升，通过类比学生很容易联想到基本图形（相似三角形），从而解决问题.对于“深入探究”板块相似问题中成比例的线段，关键是找准两组邻边.

三、推广感悟

在全等的基础上推广到相似，学生更能将两者的关系，两者各自的性质、判定理解清晰，有了全等四边形的判定结论后，学生在探索四边形相似的条件的过程中更加充满兴趣，也有了一定的方法.

《新课标》明确指出：“为了适应时代发展对人才培养的需要，数学课程要特别注重发展学生的应用意识和创新意识，同时将原先的‘双基’：基础知识、基本技能，改成了‘四基’：基础知识、基本技能、基本思想、基本活动经验，更加体现了发展学生数学能力的重要性.”

著名科学家贝弗里奇说过：“独创常常在于发现两个或两个以上研究对象或设想之间的联系相似之点.”所以，在教学过程中，教师应当善于将问题迁移、类比，提出新问题让学生研究.借助类比，将陌生对象和熟悉对象、未知规律和已知规律有机地联系起来，达到启发思维、举一反三的效果，实现认知结构的迁移，真正让学生的数学思想、能力得到提升，实现课堂的高效发展，让学生在中考中更加胜人一筹.FH