埋地悬空管道的应力分析及计算

冉龙飞，高文浩，吴 栋

（辽宁石油化工大学，辽宁 抚顺 113001）

0 前 言

由于长输油气管道服役环境复杂，管道敷设不可避免地会经过各种地质灾害频发区，管道运行存在潜在风险。例如1994年，长庆油田元-悦段输油管道受洪水冲刷，导致管道大面积悬空，另外上游的泥石流将管道冲毁26处，管道多处被拉断，导致管道停输，造成严重损失，说明埋地管道悬空是造成管道失效的主要原因之一。因为在地质灾害频发区可能存在大跨度的埋地管道悬空，在管道自重、输送介质质量等载荷共同作用下，管道出现下垂，较大的下垂高度导致管道变形，甚至拉断管道，造成严重的事故[1]。因此，研究埋地悬空管道的应力分布，对管道的安全运行具有实际意义。

1 悬空管道的受力模型

埋地悬空管道两端受到土体的弹性支撑，可将管道看作两端受弹性支撑的梁结构，因此悬空管道的受力模型可简化为变形梁模型[2-3]，如图1所示。

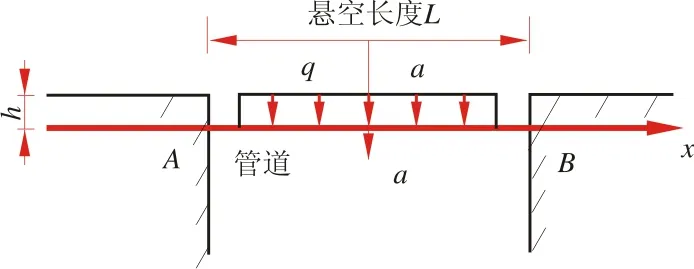
图1 悬空管道力学模型

悬空段管道受到管道自重、输送介质质量、悬空管道埋入端上方土对管道的压力等均布载荷q的共同作用，并受到集中载荷作用。基于Winkler线性理论将悬空管段两端非悬空段管道看作半无限长的弹性地基梁，近似认为土壤物性、埋地管道的受力和变形关于轴对称。

2 载荷计算

埋地管道在运行过程中受到各种载荷作用，静载荷主要包括管道自重、管道输送介质质量、防腐材料等保护层重、内压和温度变化对管道的作用、管道上覆土层对管道的作用等，动载荷主要包括地层塌陷、冲沟、滑坡、地震等地质灾害所产生的载荷[4]。

2.1 重力荷载

（1）管道自重载荷

式中：Gρ—管子的质量；

ρ—管材密度；

D—管材外径；

d—管材内径；

L—管道长度。

（2）输送介质载荷

式中：Gj—管子所含介质的质量；

ρi—输送介质的密度。

（3）防腐材料载荷

式中：Gb—管子上防腐材料质量；

ρb—防腐材料密度；

dc—防腐层的平均直径；

tb—防腐层平均厚度。

（4） 土壤载荷

2.2 应 力

实际运行状态下，悬空管道受到内外压力和温度变化的共同作用。所受应力中对悬空管道强度和稳定性造成影响的应力分别为轴向应力、环向应力和剪应力[5]。

（1）轴向应力。地下管道产生轴向应力的原因是温度的变化和环向应力的泊松效应，依照（4）式计算：

式中：σ—管道的轴向应力；

σt—管道温差产生的应力；

σa—管道环向应力；

E—管材弹性模量；

ΔT—管道温度变化量；

p—管道内压；

忘记是从哪天开始，她每天在网上冲浪的时候，他都会在。他们会谈很多心事，包括小时候的顽劣，但是，却避免着现实。

α—管道材料的线膨胀系数；

μ—泊松比；

t—管道壁厚。

（2）剪应力。局部悬空的埋地管道剪力很大，不能忽略。在埋地管道圆形横截面上下边缘处为零，在横截面中性轴处绝对值最大。局部悬空的圆形埋地管道横截面中性轴处的剪应力为：

式中：τ—剪应力；

Fz—管道竖向的总压力。

（3）环向应力。环向应力由管道输送介质内压产生，内压是确定管道应力状态的主要作用力之一，内压产生的环向应力σh为：

3 管-土相互作用关系

管-土之间相互作用，将土对管道的支撑反力用弹簧近似代替，根据场地土的性质和管道参数，采用三个方向上土弹簧表示[6-7]。

轴向弹簧刚度

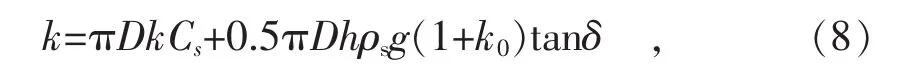
式中：k0—土静压力系数；

D—管道外径；

Cs—回填土内聚系数；

k—粘合系数；

δ—管土截面摩擦角。

横向土弹簧刚度

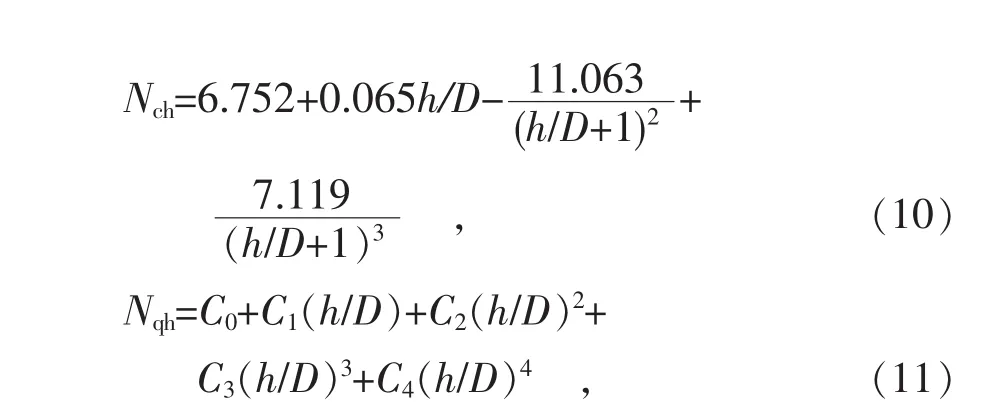
式中：C0～C4为计算Nqh的系数，按表1要求取值。

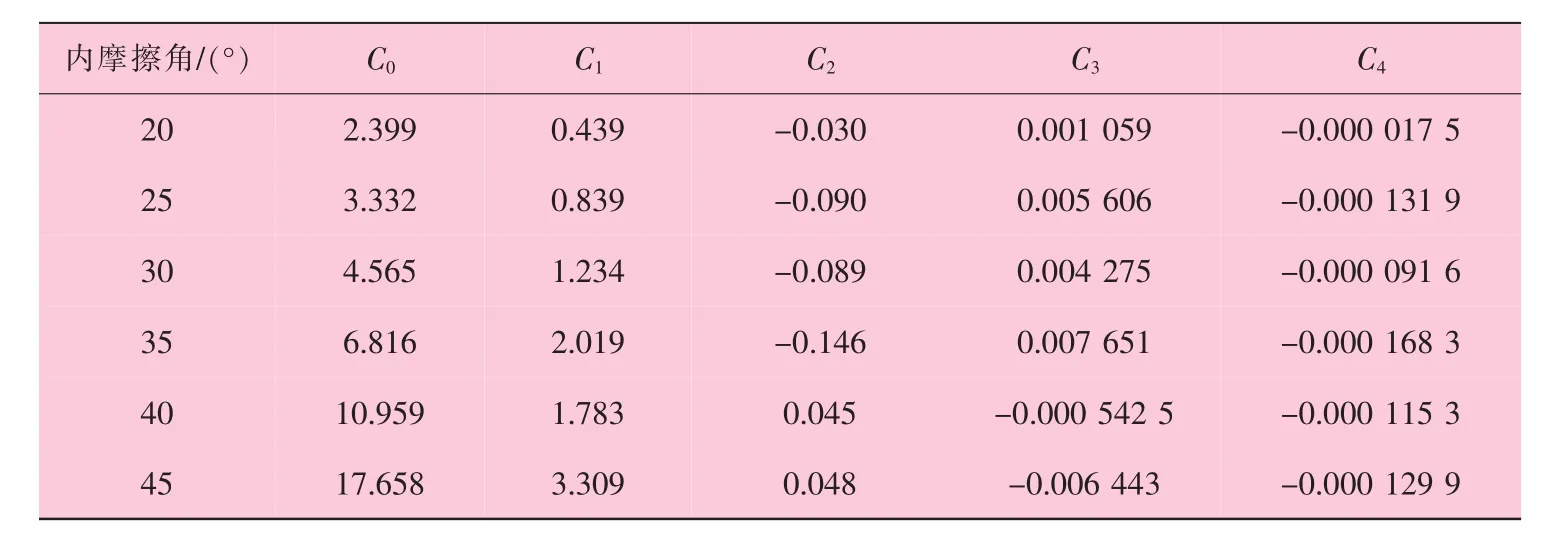
表1 计算Nqh时C0～C4的取值

竖向土弹簧刚度

式中：准—内磨擦角。

相邻土弹簧之间距离，经过反复验证，间距满足式（15）和式（16）要求时，误差可以控制在较小的范围内[5]。

式中：β—特征系数；

E—管材弹性模量；

I—惯性矩。

4 有限元计算

4.1 计算模型

管-土相互作用属于复杂的非线性问题，模拟此类问题采用ABAQUS有限元分析软件。该软件对复杂的非线性问题能够进行较为准确的计算，而且该软件开发了专门针对埋地管道的模拟单元，即管-土相互作用单元（PSI）。对悬空管道受力进行分析，计算中不考虑风载、温差、外界震动、初始装配应力等其他影响因素。ABAQUS可供选择的模拟单元有梁、管或弯接头单元。埋地管道与土壤之间的相互作用通过管-土相互作用单元来模拟[8]。本研究采用梁、管单元来模拟埋地悬空管道的受力特点。工程中采用简化模型来分析管土间的相互作用关系。目前常用的管土模型主要包括弹性地基梁、土弹簧和非线性接触三种。弹性地基梁模型基于静力分析，假设管线周围土体均匀分布，将管线视为弹性梁模型，主要考虑土体最终位移对管线的作用。弹性地基梁模型理论简单明了，易于手算，因而被工程界广泛接受，并被美国输油（气）抗震规范所采用。悬空管道两端埋入土壤中，管道向下变形过程中受到轴向力的作用，并且承受弯矩，因此采用弹性地基梁模型，模拟实际悬空管道工况。埋地管道土层运动情况通过管-土相互作用单元（PSI）来模拟，如图2所示[9-10]。

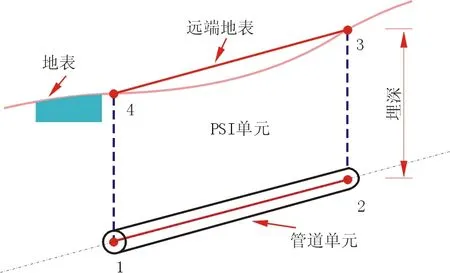
图2 管-土相互作用单元简图

该单元只有位移自由度，该单元的一面或者一边与下面的模拟管道的梁、管或弯接头单元共用节点，而另一侧的节点代表代表地面，并用于施加边界条件来描述远场地面的运动。悬空管道埋入端土对管道的地基抗力用具有一定刚度的弹簧近似代替。

4.2 参数选取及载荷计算

参数：管材钢级X70，管径1 219 mm，壁厚18.4 mm的埋地悬空管道，设计压力12 MPa，弹性模量210 GPa，泊松比0.3，惯性矩7.8×10-4m4。管材密度7 800 kg/m3，最小屈服强度483 MPa，埋深1.5 m。土壤密度1 900 kg/m3，土壤地基系数为40 000 kN/m3，土内摩擦角为30°。

计算得出管道所承受载荷：管道自重Gp=5.3×103N/m；埋地段管道上方土层的重力q=3.4×104N/m。

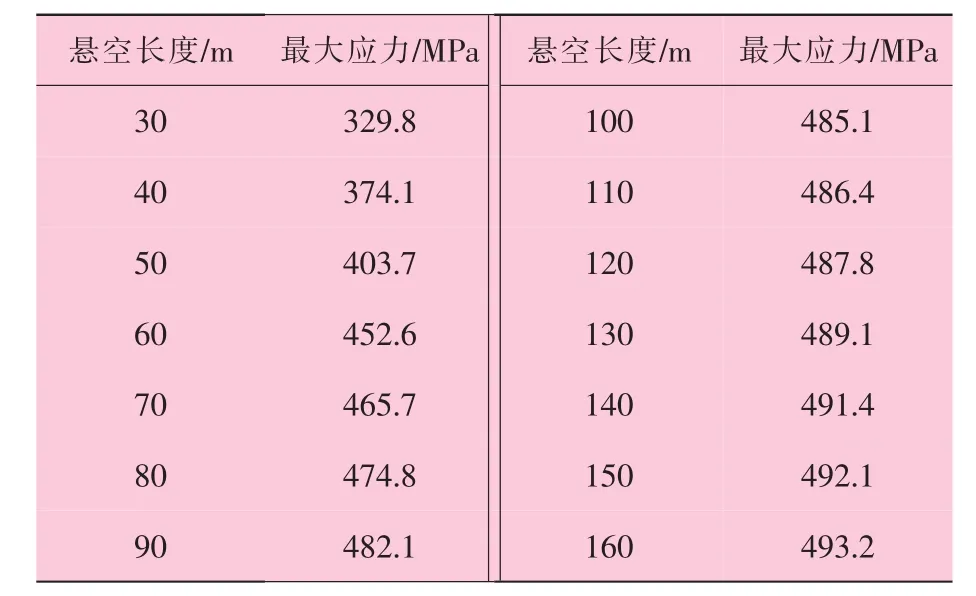
表2 不同悬空长度下管道的最大应力和最大位移

4.3 计算结果

运用ABAQUS有限元软件计算得出埋地管道在不同悬空长度下管道的最大应力，见表2。

根据表2中的应力取值，可见随着管道悬空长度的增加，管道应力也在增加，如图3所示。该管材管道规定的最小屈服强度为483 MPa，分析得出管道在悬空长度L=90m时，管道的屈服强度为482.1 MPa，管道材料接近于屈服阶段。

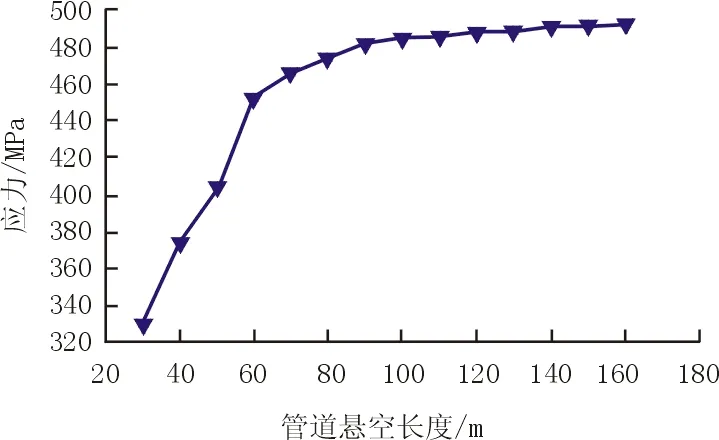
图3 不同悬空长度下管道应力变化曲线

5 结 论

悬空管道埋入端采用弹性地基梁模型，通过理论计算得到埋入段上覆土的重力和何种重力载荷。管-土相互作用通过弹簧近似代替，采用GB 50470—2008《油气输送管道线路工程抗震技术规范》，计算得到悬空管道埋入段在横向、轴向和竖直方向上土弹簧刚度。运用ABAQUS有限元软件计算得到该材质管道在悬空长度L=90 m时，近似接近于屈服阶段。说明采用基于应力的管道设计方法存在局限性，因为管道在屈服阶段，管道应力变化不显著，在该阶段对管道作出安全评定时应采取基于应变的设计方法。

[1]罗金恒，赵新伟，王峰会，等.地质灾害下悬空钢管的应力分析及计算[J].压力容器，2006，23（04）：23-26.

[2]王峰会，赵新伟.高压钢管黄土塌陷情况下的力学分析与计算[J].油气储运，2004，23（04）：6-8.

[3]由小川，庄茁，张效羽，等.高压天然气管线在地质灾害下的失效分析[J].天然气工业，1999，19（04）：77-81.

[4]王小龙，姚安林.埋地钢管局部悬空的挠度和内力分析[J].工程力学，2008，25（08）：218-222.

[5]杜景水，马廷霞，王维斌.基于小挠度理论的悬空管道力学分析[J].油气储运，2009，21（07）：16-18.

[6]童华，祝效华，练章华，等.坍塌和冲沟作用下埋地管道大变形分析[J].石油机械，2007，35（11）：29-32.

[7]博雷西 A P，赛德博 O M，西利 F B，等.高等材料力学[M].北京：科学出版社，1987：39-67.

[8]唐永进.压力管道应力分析[M].北京：中国石化出版社，2003.

[9]马廷霞，吴锦强，唐愚，等.成品油管道的极限悬空长度研究[J].西南石油大学学报，2012 （04）：165-173.

[10]赵林，冯启民.埋地管线有限元建模方法研究[J].地震工程与工程振动，2001，21（02）：53-57.