基于模糊数学的发电权交易多目标函数优化算法

潘艳霞

(山西省电力公司电力交易中心，山西太原 030001)

发电权交易是我国减少水电弃水、实施电源结构调整、促进节能减排目标实现的产物.目前的研究工作主要集中于对发电权交易模型的研究，包括经济效益最大化模型、节能量最大化模型以及网损最小化模型.这3类模型中，经济效益最大化模型考虑了发电权交易的经济性，但能耗特性不太理想且未顾及电网安全性;节能量最大化模型能耗降低量最大，但牺牲了一定的经济效益;网损最小化模型只注重电网安全性，对经济效益及节能量均未考虑.［1］

针对以上问题，本文综合考虑发电权交易的经济性、节能性以及电网安全，将效益、煤耗和网损3个参数结合起来，提出了在役机组发电权交易的多目标函数模型.模糊数学是用精确的数学方法表现和处理实际客观存在的模糊现象的方法，对多目标函数的求解问题同样适用，［2］本文使用该方法对所建立的综合多目标函数进行求解.［2］

1 在役机组发电权交易模型分析

1.1 基于经济效益最大的发电权交易模型

发电权交易，即计划合同电量的有偿出让和买入.交易双方在平等自愿的原则下，不影响电力消费者利益前提下，采取双边交易或集中交易的方式完成电量指标的买卖.［3］

完全市场条件下发电权撮合交易的目标函数为经济效益最大化，其基本原理为优先撮合报价较高的发电权出让机组与报价较低的受让机组进行交易，选择交易一方总交易量为决策变量，通过对其求解，可得出实现总交易效用最大的交易结果.不考虑其他市场和网络的约束，其数学模型为:

式中:m——受让方总数;

n——出让方总数;

bi——受让方i的申报价格;

bj——出让方j的申报价格;

Qi——受让方i实际的买入电量;

Qj——出让方j实际的售出电量;

QBi，QSj——受让方与出让方的申报电量.［4］

1.2 基于节能量最大的发电权交易模型

节能量最大模型是优先满足煤耗较高的发电权出让机组与煤耗较低的受让机组进行交易，将节能量最大化作为发电权交易的目标更有利于现阶段政策背景下节能降耗以及顺利关停小火电、减排增效等，达到优化电源结构、降耗减排的目的.［3］

该数学模型的目标函数为:

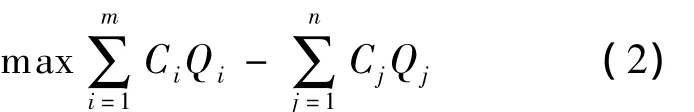
约束条件如下.

(1)电量约束:Qi≤QBi，Qj≤QSj;

(3)单个交易价格约束:bi≥bj;

式中:Ci——受让方i的平均供电煤耗;

Cj——出让方j的平均发电煤耗;

CT——最小能耗值.

1.3 网损最小化模型

网损最小化的模型为:

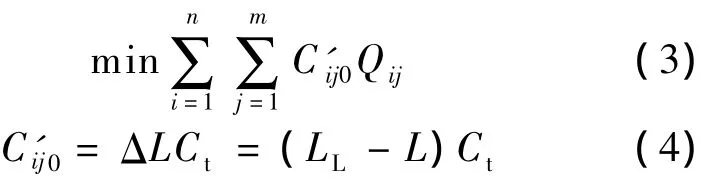
式中:C'ij0——发电权转让交易引起的网损变化成本;

Qij——交易电量;

Ct——单位购电价;

L——交易前的电网网损;

LL——交易后的电网网损;

LL-L——整个发电权交易前后电网网损的变化.

在建立模型时，应考虑网损变化对交易的影响，以及网损成本的增加给交易各方所带来的效益损害.对使网损增加较大、影响到系统安全稳定性的交易，应适当降低其优先级.［4］

1.4 综合多目标发电权交易模型

为了同时兼顾到交易各方利益最大、成交电量最大、煤耗、网损最小化，并考虑交易量约束、电网安全约束、供电可靠性及供电质量方面的约束，建立了在役机组发电权交易的综合多目标模型.

基于社会效益、煤耗、网损最优的发电权交易的目标函数为:

Fij——煤耗总和;

Cij0——网损总和.

发电权交易的约束条件如下.

(1)电厂i所申报的出售发电权交易的数量约束:

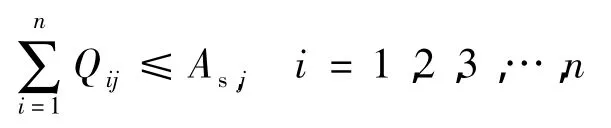
(2)购买方j申报的购买的发电权数量约束:

(3)电网的支路功率极限约束、节点电压约束以及供电质量约束:

式中:As，j——电厂i所申报的出售发电权交易的数量;

AB，i——购买方j申报购买的发电权数量;

Pl——电网支路功率;

Pl，max——电网支路功率最大值;

V，Vk，min，Vk，max——节点电压、节点电压最小值、节点电压最大值;

F，Fmin，Fmax——供电质量、供电质量的最小值、供电质量的最大值.

2 模糊数学法求解多目标函数

在多目标优化的问题中，多目标最优解应包含各子目标的贡献，但各子目标之间往往彼此矛盾，一般很难同时达到最优.各子目标最优解与多目标最优解之间的相互关系是模糊的，很难有一个确定的界限，从而无法直接比较优劣，所以需采用模糊数学来解决多目标优化的问题.［5］

2.1 求解思路

利用模糊数学法解决多目标优化问题，先求出各子目标在所有约束条件下的最优解，然后再利用这些最优解将各子目标函数模糊化，称为确定隶属函数，以求得交集的隶属度函数取最大值的解，这个求得的解就是多目标优化问题的最优解.

2.1.1 隶属度函数的确定

模糊数学是用精确的数学方法表现和处理实际客观存在的模糊现象，首先确定隶属度函数u.对于上述4个目标函数，本文采用降半Γ形分布的隶属度函数，其公式为:

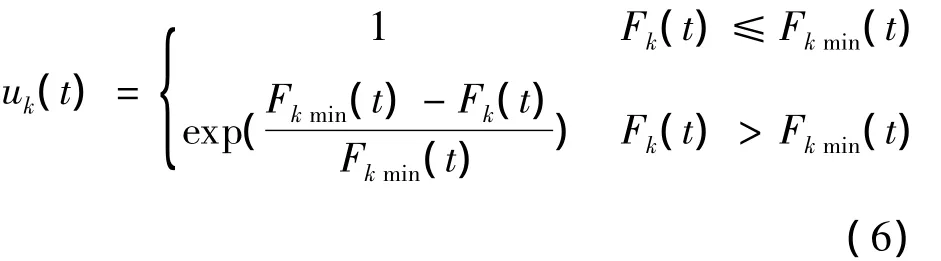
式中:Fkmin(t)——单目标函数Fk(t)在约束条件下的最小值;

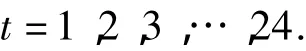
2.1.2 模糊模型的建立

引入模糊隶属度变量u之后，根据最大隶属度原则，将模糊的多目标优化问题转化为非线性的单目标优化问题，使综合多目标交易模型变为:

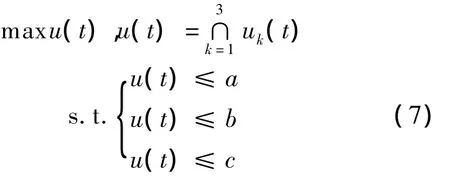
式中:u(t)——模糊优化满意度;

a——发电成本满意度;

b——成交价格满意度;

c——环境成本满意度.

采用加权组合法对多目标函数进行求解，采用加权组合后的目标函数为:

对于目标函数的加权求和结果进行大小排序，所得数据大小即为撮合的优先级，优先对数据大的交易对进行撮合交易，将所有满足配对条件的交易对进行撮合，目标函数的系数a，b，c分别为权重因子，适当确定权重a，b，c能够利于得到合理的交易组合，兼顾各方的利益达到收益的平衡点.

2.2 模型求解

在模型求解中，对效益、煤耗和网损数据进行加权处理，分下面3种情况:

(1)当权系数a为最大值时，权重偏重社会效益，目标函数以社会效益为主，煤耗和网损占的成分比较少;

(2)当权系数b取值较大时，权重偏向在煤耗上，社会效益和网损占的成分比较少;

(3)当权重c取值较大时，是主要考虑降低系统的网损，体现的是电力公司的利益.

对所得到的撮合交易对经调度中心安全校验进行阻塞管理，验证交易的实施，考虑是否会使系统的运行存在安全隐患，如果支路超负荷，应调整相对的交易量.

3 算例分析

本文算例以某电力调度辖区系统进行计算(网损率按1.19%，煤价按800元/t计算)，选取其中6台机组为在役机组发电权交易对象进行模拟交易，

表1为参与发电权交易的发电厂的申报数据.［6］

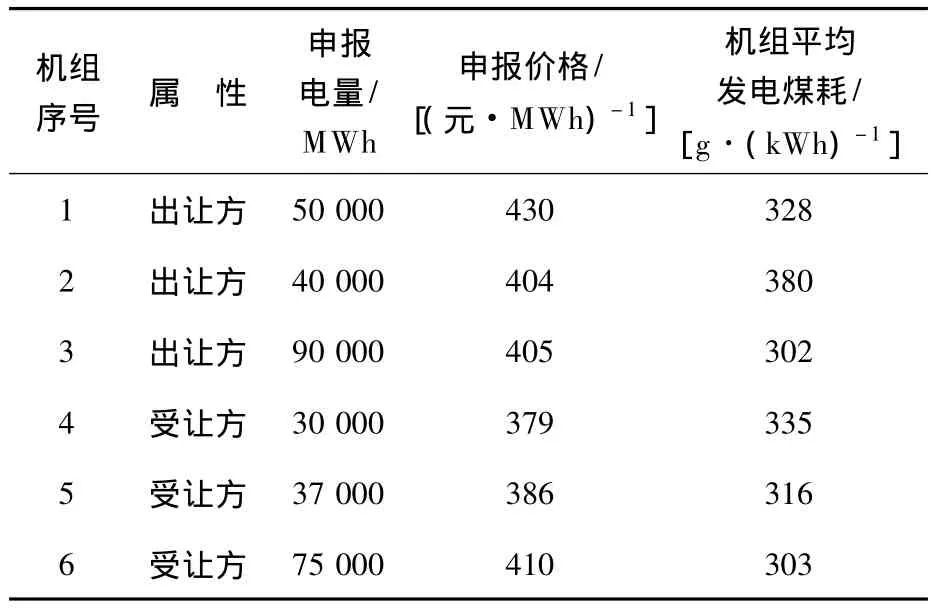
表1 市场成员申报数据

分别运用传统的经济效益最大化模型、节能量最大模型和本文提出的基于模糊数学的发电权交易多目标函数优化算法对算例进行计算分析.

(1)经济效益最大化模型 该模型以经济效益最大化为目标，其撮合结果如表2所示.

表2 经济效益交易最大化模型交易结果

(2)节能量最大化模型 该模型以经济效益最大化为目标，其撮合结果如表3所示.

表3 节能量最大化模型交易结果

(3)基于模糊数学多目标函数优化算法 以节能减排为指导思想，取 a=0.2，b=0.5，c=0.3进行计算，根据加权结果的大小进行优先排序，优先安排函数值大的交易对，交易结果如表4所示.

为更直观地比较3种交易模型的交易结果，本文将节能量指标按照标准煤单价(800元/t)转化成节省燃煤成本作为交易的社会效益，并以综合经济效益作为评价交易结果的综合指标，交易结果如表5所示.

由此可见，经济效益最大化模型充分考虑了发电权交易的经济性，但系统能耗特性的改善不是特别理想;节能量最优模型可更大程度地降低整个系统的能耗，但同时牺牲了较多的经济性;而基于模糊数学的多目标函数优化算法较好地兼顾了发电权交易的经济性和节能降耗要求，达到了具有更广泛意义的效益最优.

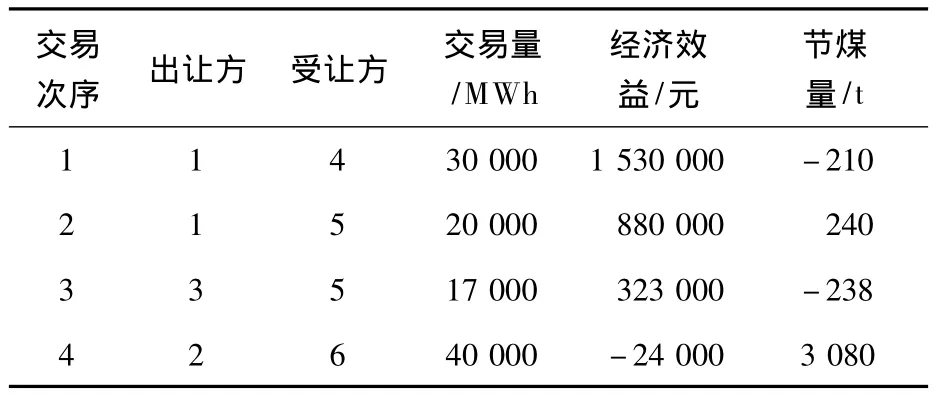
表4 基于模糊数学的多目标函数优化算法交易结果

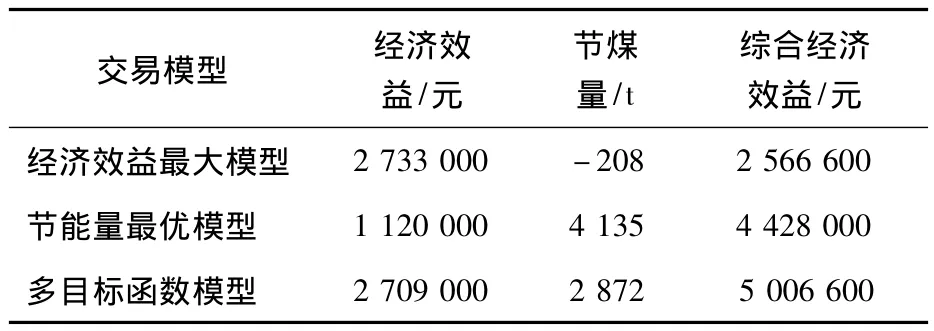
表5 3种交易模型的交易结果比较

4 结语

本文提出的基于模糊数学的发电权交易多目标函数优化算法，综合考虑了发电权交易的经济效益、煤耗以及输电网损，可根据实际需要设定不同的系数，从而更好的调节市场，优化资源配置.

［1］ 尚金成，何洋.基于节能减排的发电权交易理论及应用［J］.电力系统自动化，2009，33(13):37-42.

［2］ 张世帅，张学松.发电权交易下的节能减排指标设计及应用分析［J］.电网技术，2010，34(11):156-160.

［3］ AI Dongping，BAO Hai.Congestion dispatching model and a new trade mode for generation rights trade［J］.IEEE，2010(5):1-5.

［4］ 曾鸣，史连军.与市场机制相协调的节能发电调度相关问题研究［J］.电力技术经济，2007，19(5):7-11.

［5］ 王雁凌，程倩.基于节能降耗的发电权交易模型［J］.电力系统保护与控制，2010，38(18):28-32.

［6］ 郑欣，蒋传文.网损系数法在发电权交易成本计算中的运用［J］.华东电力，2009，37(1):150-153.