基于改进粗糙集理论与概率神经网络的变压器故障诊断研究

江玉蓉，葛永丰

(1.上海电力学院电气工程学院，上海 200090;2.核电秦山联营有限公司运行部，浙江嘉兴 314300)

电力变压器的故障表象与机理间的联系错综复杂，单一的诊断方法均存在一定的弊端，因此可以考虑将几种判断方法结合起来分析.同时，在进行变压器故障诊断时所得到的信息往往是不完备、不准确的，而且其中还有一些冗余信息，如何除去这些冗余信息就成为研究的重点.于是粗糙集(Rough Set)理论被引入变压器故障诊断模型中，但通常人们都是运用粗糙集理论的代数观点，可能得到多个最小属性集.如文献［1］利用粗糙集理论约简变压器故障决策表，得到了4个最小属性集，然后根据征兆获取的难易程度选择故障诊断模型，以抉择最小约简表，这种方法带有很大的人为因素.本文采用可辨识矩阵的理论对变压器故障决策表进行约简，得到唯一的最小决策表，并将该最小决策表引入改进的概率神经网络(Probabilistic Neural Network，PNN)的训练与仿真中，这样不仅能够减少神经网络的训练内容，而且能够更加准确地建立故障诊断模型.

1 粗糙集理论及其约简

1.1 粗糙集的基本概念

粗糙集理论是用于分析和处理各种不完备信息，从中发现规则、揭示潜在规律的数学工具.它能够利用数据本身提供的信息，而不需要其他任何的先验知识.因此，它为处理变压器故障诊断专家系统这种模糊的和不精确的知识提供了一条全新的途径.

一般来说，条件属性是对事物特征的描述，比较容易获得;决策属性描述的是事物的类别，是对事物进行分类的依据.粗糙集理论就是发现并定量描述事物的特征与分类之间对应关系的理论.

定义1 对一个知识表达系统 S={U，A，{Va}，f}，如果f:U→Va是一个信息函数，这样的“属性-值”对就构成了一张二维表，称之为信息表;如果A由条件属性集C和决策属性集D组成，并且满足A=C∪D，C∩D=Φ，则称S为决策系统，构成一种特殊的信息表——决策表.

知识约简是粗糙集理论的核心内容之一.所谓知识约简，就是在保持知识库分类能力不变的条件下，删除其中不相关或不重要的冗余知识，以简化判断规则.

定义2 若存在Q=P-r，Q⊆P，Q是独立的，满足ind(Q)=ind(P)，则称 Q为P的一个约简.

1.2 可辨识矩阵的基本概念

令S={U，A，{Va}，f}是一个决策系统，U 为论域且 U={x1，x2，x3，…，xn}，D 是决策属性，a(x)是记录 x在属性 a 上的值，cij(i，j=1，2，3，…，n)表示可辨识矩阵中第i行第j列的元素.这样可辨识矩阵可定义为:

式(1)表明，可辨识矩阵的元素是由3种值组成的.当决策表中两条记录的条件属性不同且决策也不相同时，该元素值为属性不同的属性组合;当两条记录的决策相同时，该元素值为零;当条件属性相同而决策不同时，称该决策表是不一致的.

1.3 可辨识矩阵的约简

从前文可知，可辨识矩阵中包含了决策表的全部信息，故在其基础上进行属性约简与直接在论域中进行约简可以达到同样的效果.若矩阵中某一个元素所包含的属性个数(即属性组合数)为1，则表明除了该属性外其余属性无法将信息表中决策不同的两条记录区分开来，即该属性必须保留.因此，矩阵中所有属性组合数为1的属性均为决策表的核属性(可能为空).［2-4］

将可辨识矩阵M中含有至少一个核属性的项置零(因为它们都是只要由核属性就能够区分，而不必用到其余属性的信息)，得到一个新的矩阵M'.此时的M'表示必须根据核属性之外的属性才能判断对象间的关系.M'中的所有项均为零则表示论域中所有的对象都能区分开.再按照如下准则来指导对剩余属性的选取:将矩阵M'中各剩余属性在各个包含属性个数最少的项中出现的次数最多者优先放入约简集合当中;若出现的次数相同，则在这些出现次数相同的属性中选择包含属性个数为次数最少的项中出现的次数最多者，依此类推.

可以发现，可辨识矩阵对约简决策表、去除决策表中的冗余属性具有非常好的收敛效果，这对去除变压器中的冗余故障征兆能够起到非常明显的作用.

2 概率神经网络的构建

概率神经网络结构如图1所示.网络共分为输入层、径向基层和竞争层3层.输入层将特征向量传递给网络;径向基层首先将由输入节点传来的输入数据进行加权求和，然后通过线性算子运算后传给竞争层，其神经元个数与输入训练样本向量数相同;竞争层传递函数的功能是找出输入向量中各元素的最大值，使与其最大值相对应类别的神经元的输出值为1，其他神经元输出全部为零.［5］

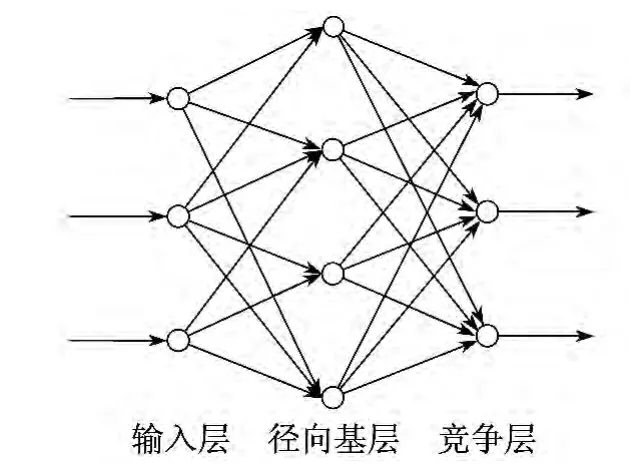
图1 概率神经网络结构

与BP人工神经网络相比，概率神经网络的主要优点有:训练速度快，因为PNN是一次完成，没有学习过程;无论分类问题多么复杂，只要有足够的训练数据，就能够保证获得贝叶斯准则下的最优解;允许增加和减少训练数据而不需要重新进行长时间的训练.基于以上优点，本文采用概率神经网络来构建诊断模型，并且为了能减小训练复杂度，提高诊断的正判率，还将去除冗余属性后的最小决策表引入概率神经网络的训练与仿真中.另外，进一步改进该神经网络，将径向基层的传递函数非线性化，这样能够避免贝叶斯网络最大解重复时出现的逻辑矛盾.

3 电力变压器故障诊断模型

变压器故障诊断的基本思想是将观察或测量到的变压器故障征兆作为对故障分类的条件属性，将实际存在的故障作为决策属性建立决策表.首先，根据变压器故障信息数据形成征兆集合与故障集合，并对上述两个集合进行分析，得出变压器故障诊断的决策表.然后，根据故障诊断决策表形成可辨识矩阵，并采用上述的可辨识矩阵约简粗糙集的方法对该矩阵进行约简，得到最小决策表.最后，将该最小决策表当作训练样本，作为竞争层的输出信息，引入构建完毕的改进概率神经网络中进行训练与仿真，从而建立完整的变压器故障诊断模型.

3.1 决策表的形成与约简

［6］及电力变压器故障的历史资料和经验，可以得出故障征兆集合(条件属性集)与故障集合(决策属性集)，分别见表1和表2.

表1 条件属性集

表2 决策属性集

对照表1和表2，并分析其中故障征兆与故障决策间的隶属程度，形成决策表如表3所示.

表3 故障诊断决策

表3中，条件属性1表示出现该故障征兆，0则为不出现，同时对故障进行编号.

根据上述的可辨识矩阵理论形成可辨识矩阵如下:

由该可辨识矩阵可得出该决策表的核属性为m1，m2，m4，则 C0={{m1}{m2}{m4}}.将可辨识矩阵中所有至少含有一个该属性的项置零，并根据上述理论进一步约简决策表得到唯一最小决策表如表4所示.

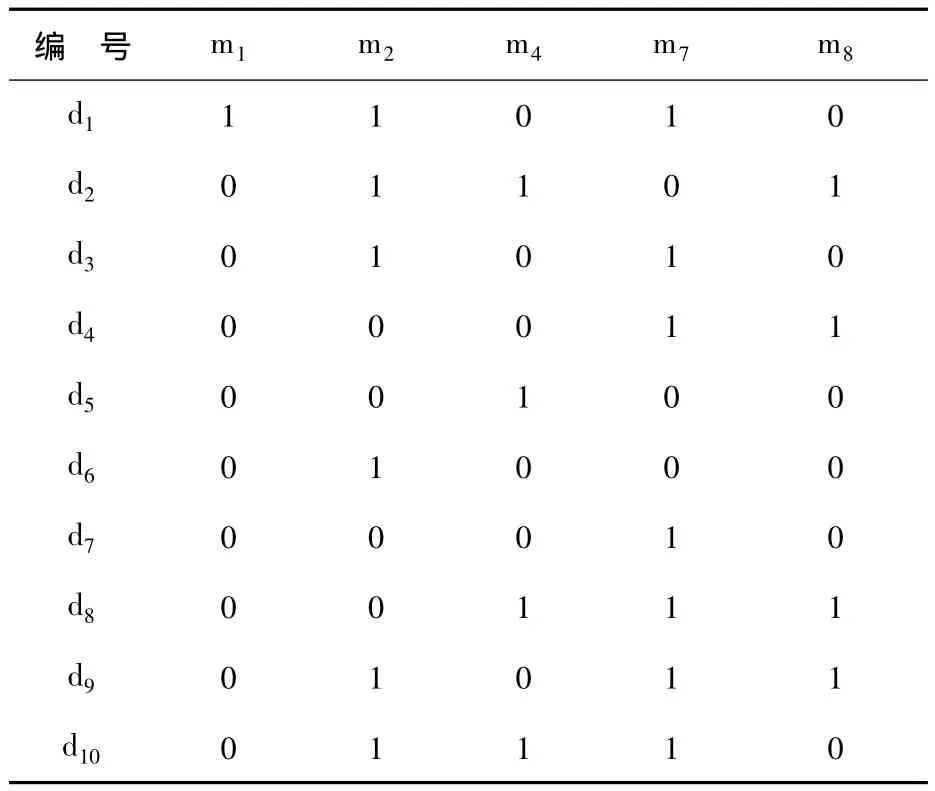
表4 最小决策

3.2 概率神经网络模型的构建与训练仿真

根据表4构建的概率神经网络模型如图2所示.将故障征兆 m1，m2，m4，m7，m8作为网络训练时输入层的输入信息，d1～d10作为竞争层的输出信息，1表示该故障存在，0表示该类故障不存在.该神经网络的输入层个数为5，径向基层神经元个数(即训练样本个数)为10(已将其传递函数非线性化)，竞争层神经元个数为10.

将已约简的最小决策表当作训练样本，对概率神经网络进行训练.并利用Matlab的神经网络工具箱中的newpnn(P，T)函数建立PNN模型进行仿真.利用PNN网络进行训练后得到的样本误差平方和变化曲线如图3所示.

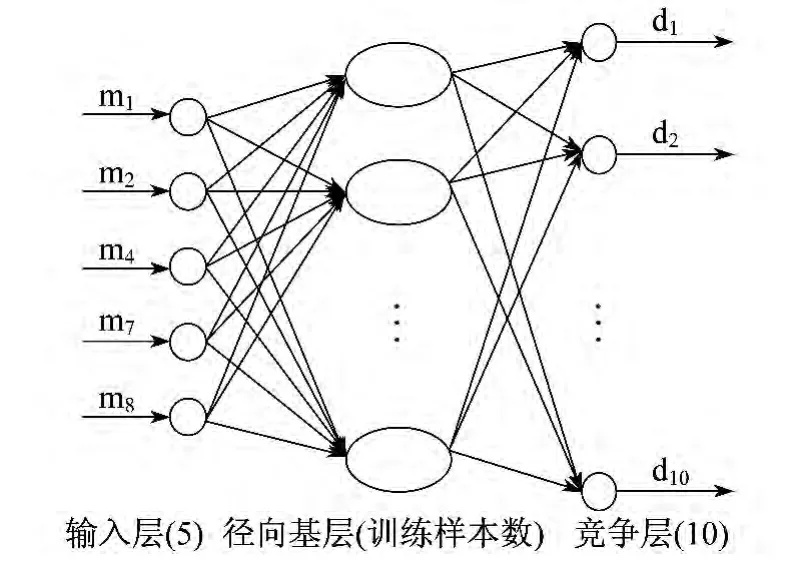
图2 概率神经网络模型

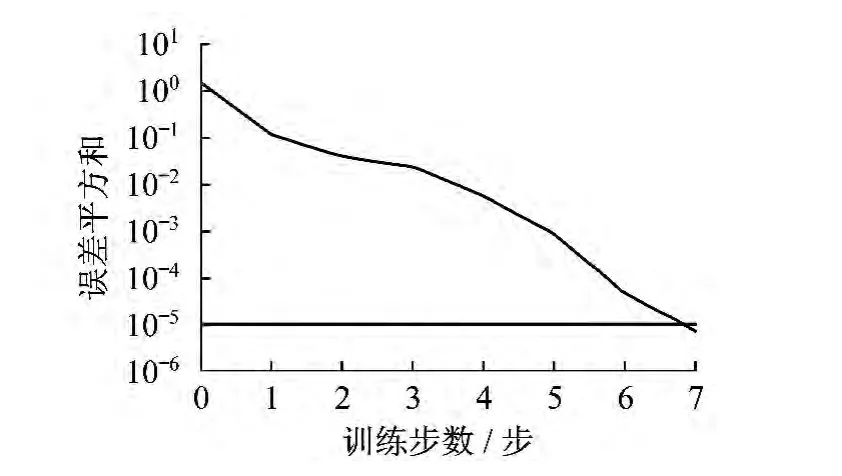
图3 PNN网络误差平方和变化曲线

由图3可以看出，利用了最小决策表以后的概率神经网络具有极高的收敛性.

4 变压器故障诊断实例

惠州某变电站3#主变压器型号为ODFSZ-250 000/500，投入运行后一年的周期性试验中发现3#主变压器B相C2H2含量超标，并且逐渐升高.随后进行油色谱、微水量、铁心接地电流等跟踪试验，实验数据见表5.

由表5可以看出，总烃含量还没有超标，φ(CO)/φ(CO2)的比值也在正常范围内，三比值分析结果为 φ(C2H2)/［φ(C2H4)］=2.0，φ(CH4)/［φ(H2)］=0.186，φ(C2H4)/［φ(C2H6)］=6.67，则其编码为102，判断存在局部放电，故障编码为{0 0 0 1 0}.用设计好的Matlab概率神经网络进行仿真，得到结果为悬浮放电故障.在吊芯检查时发现，该变压器故障为夹件松动，产生悬浮放电所致，可见PNN诊断结果与实际情况一致.

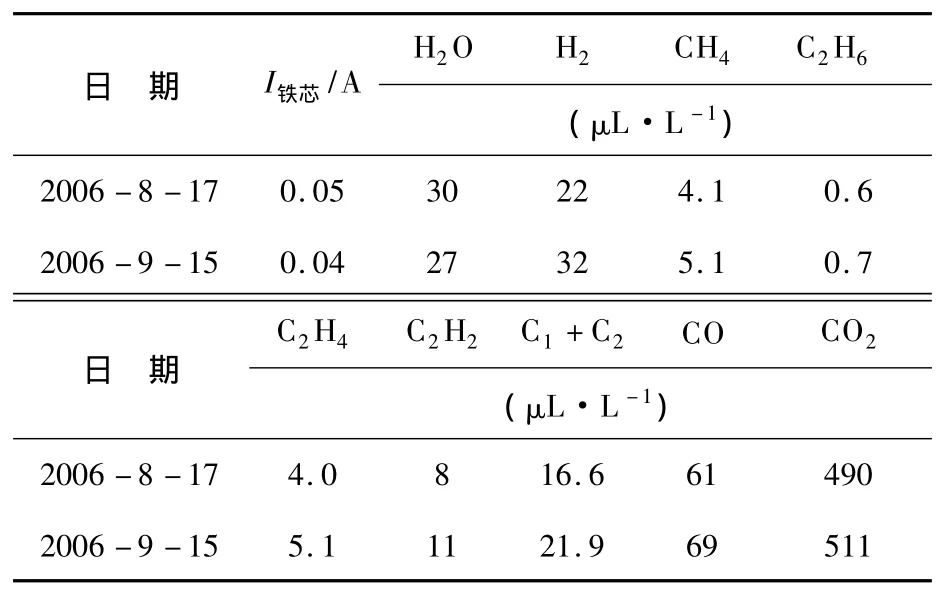
表5 3#主变压器B相试验结果

根据本文提出的诊断方法，笔者在一些文献中搜集典型的故障样本对本模型进行测试，结果见表6.可以发现，该模型诊断精度比目前常用的三比值法高，故障定位相对精确.

表6 诊断结果比较

续表6

5 结语

本文将可辨识矩阵引入到粗糙集故障诊断决策表的约简中，利用可辨识矩阵的对称性减小决策表约简的复杂度，提高了约简效率.结合概率神经网络的高速收敛性，构建了一个新变压器故障诊断模型.实际结果表明，该方法不仅在一定程度上节约了故障诊断过程中的空间与时间，而且能够在属性缺失的情况下较为准确地判断故障情况.

参考文献:

［1］ 王永强，律方成，李和明.基于粗糙集理论和人工神经网络的电力变压器故障诊断方法［J］.中国电机工程学报，2006，26(8):137-141.

［2］ 赵冬梅，韩月，高署.电网故障诊断的决策表约简新方法［J］.电力系统自动化，2004，28(4):63-66.

［3］ 梁福才，林成龙.粗糙集属性约简的完备算法［J］.电光与控制，2007，14(2):59-72.

［4］ 张振林，黄明.一种高效的简化可辨识矩阵集成算法［J］.大连交通大学学报，2007，28(1):46-49.

［5］ 段慧达，王建男，白晶.基于动态对角递归网络的变压器故障诊断［J］.微计算机信息，2007，28(6):214-215.

［6］ 杨莉，钱政，周跃峰，等.基于节约覆盖集理论的电力变压器绝缘诊断模型［J］.西安交通大学学报，1999，33(4):23-26.