浅谈数形结合在小学数学中的运用

◆施艳艳

(金华市浦江县浦阳二小)

一、数形结合——形成概念的好帮手

形成概念就是学生从许多具体事例中以归纳的方式概括出一类事例的本质属性。学生不能形成概念主要是因为没有经历“将丰富的感性材料加以去粗取精、去伪存真、由此及彼、由表及里”的改造过程，数形结合能使比较抽象的概念转化为清晰、具体的事物，从而让学生更好地发现事例的本质属性或规律。

例如，教学“三角形的认识”一课，可以这样引导学生形成概念:

交流:这节课重点研究三角形(板书:三角形)，你在哪里见过三角形?你对三角形已经有哪些了解?

引导:你会画三角形吗?请闭上眼睛用彩色笔在纸上画一个大小适中的三角形。

展示:选择三幅典型的图。

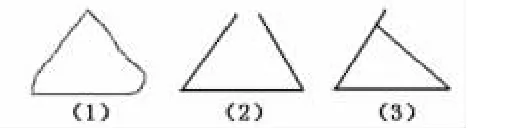
评析:这三幅图是你印象中的三角形吗?为什么?

交流:图形(1)中三条边不是线段，图形(2)不是封闭图形，图形(3)中两条线段的端点没有重合。

思考:你认为三角形是怎样一种图形?

板书:由三条线段围成的图形(每相邻两条线段的端点相连)叫三角形。

利用数形结合，帮助学生很快形成了“三角形是怎样一种图形”的概念。

二、数形结合——化解难点的好帮手

化解难点就是分解教学难点，做到化难为易、由浅入深、直观形象。学生不能化解难点主要是因为不能实现将抽象的内容具体化、形象化、直观化，数形结合能够化抽象为具体、化复杂为简单、变生疏为熟悉、变深奥为浅显。

例如，教学一道练习题:在一个圆柱形储水桶里，把一段半径是5厘米的圆钢全部放入水中，水面就上升9厘米;把圆钢竖着拉出水面8厘米后，水面就下降4厘米。求圆钢的体积。

分析与思考:仔细读题，题目的意思还真是有点难理解。为了帮助学生理解题意，我一共画了三幅图。首先，画一个圆柱形储水桶，原来有一些水(图1);接着，将一个底面半径为5厘米的圆钢全部放入水中，水面上升了9厘米，引导学生观察思考:圆钢的体积就相当于上升的水的体积;最后，又出示了第三幅图，将圆钢拉出8厘米，水面下降了4厘米，说明拉出的一部分圆钢体积就等于下降的水的体积。然后引导学生仔细观察这三幅图，并思考:“可以从何处入手呢?”

一些学生通过观察，动脑筋想出了解决问题的办法:先求拉出水面圆钢的体积，也就是下降了4厘米水的体积，5×5×3.14×8=628(平方厘米);再求出圆柱形储水桶的底面积，628÷4=157(平方厘米);最后求上升了9厘米水的体积，也就是整个圆钢的体积，157×9=1413(平方厘米)。我表扬了这些学生善于观察、善于思考，同时激发学生思考:“解决这一问题，你还有更简便的方法吗?”经过思考，生1发现了这样的方法:“圆钢拉出水面8厘米，水面就下降了4厘米，8厘米正好是4厘米的2倍;而将圆钢全部放入水中时，水面上升了9厘米，说明圆钢的高度是9厘米的2倍，也就是18厘米!那求圆钢的体积就很简单了，即5×5×3.14×18=1413(平方厘米)。”生2想到:“可以将圆钢看作两段，水面以上的为一段，水面以下为一段(如图2)，这两部分都沉入水中后，水面上升9厘米;一部分圆钢到了水上，水面就下降了4厘米，那水下的那部分圆钢，就相当于(9－4)=5(厘米)水的体积。根据4:5的关系，用8÷4×5=10(厘米)求出圆钢在水面以下的高度，再用(8+10)×5×5×3.14=1413(平方厘米)就可以求出圆钢的体积。”也许受刚才同学的启发，生3又想到一种方法:“求出水面以上的圆钢体积，因为4厘米占9厘米的，说明露在水面以上的圆钢体积也是占整个圆钢体积的，可以得到5×5×3.14×8÷4/9=1413(平方厘米)。”

课上，学生创新思维的火花不断闪烁，来自于教师的巧妙引导与激发，更来自于教师为学生构建起的桥梁——“数形结合”。

三、数形结合——解决问题的好帮手

解决问题就是综合性、创造性地应用已学数学知识和方法解决陌生的、新的问题情境的过程。学生不能解决问题主要是因为不能正确理解问题情境和抽象的数量关系，数形结合能把抽象数量关系用最恰当、最清晰的图形表示出来，化抽象为直观、化繁杂为简单、化隐含为显见。

例如，在一次数学练习课中，老师出了如下一题:一块长1米20厘米、宽90厘米的长方形铝片，剪成直径为30厘米的圆片，最多可以剪几块?

学生列式为120×90÷［3.14×(30/2)2］≈15(块)

大家都以为这样列式是对的。原因是学生从已有知识出发，按常规的解题思路，用长方形面积除以圆的面积。

师:这个算式是错误的。请同学们想一想为什么错了呢?到底应该怎样解?

同学们陷入了沉思:我们认为是对的，为什么老师说是错误的呢?究竟应该怎样解呢?

当学生经过苦苦思索，不得其解时，正是老师启发诱导的极好时机。

这时教师予以点拨:请同学们联系生活实际进行思考，看看有没有不同的解法?

这一诱导掀起了学生的思维浪潮，大家七嘴八舌，议论纷纷。几分钟后，一个学生举手发言:(120÷30)×(90÷30)=12(块)

于是老师请这位学生说说是怎样想的，他上讲台在黑板上边画图边说算理，说得思路清晰、算理明白。最后该生小结:解决此类问题，最好应用数形结合的方法，这题算理是长方形的长120厘米是这个圆的直径30厘米的4倍，宽90厘米是这个圆直径30厘米的3倍，也就是在这个长方形里，横着剪，一排只能剪4个圆;竖着剪，一列只能剪3个圆，这个长方形最多只能剪3×4=12(个)这样的圆。

在整个交流过程中，“数”借助“形”轻而易举地解除了学生的困惑，使大家实实在在体验到了数形结合方法的魔力。

数形结合不仅是小学数学教材编排的一个重要特点，更是小学生解决问题常用的方法之一，同时又是一种数学思想。在教学过程中，我们教师应做个有心人，充分利用“一图抵百语”的优势，向学生渗透“数形结合”的思想，引领学生走进数学的神奇殿堂!

［1］［美］加里·D.鲍里奇.《有效教学方法》(第四版).江苏教育出版社，2002.

［2］刘加霞，王淑芳.小学数学教学与思维能力培养.华艺出版社.

［3］王珍.让直观与抽象交相辉映.福建教育，2008，(6).

［4］顾娟.浅析小学数学课堂中的“数形结合”.小学教学参考，2009，(3).