基于样本熵和支持向量机的短期风速预测模型
林常青,上官安琪,徐 箭,许 梁
(1.湖北省电力公司,湖北 武汉 430077;2.武汉大学 电气工程学院,湖北 武汉 430072)
随着风电场规模的不断增大和风电技术的不断发展,为了保证电力系统的稳定运行和可靠供电,必须对风电进行可靠的规划和调度[1]。然而风能的随机、间歇不确定性使风电的规划和调度面临新挑战[2]。对风电场风速的有效预测有利于及时调整调度计划,减少电力系统运行成本和旋转备用,减轻风电接入对电网的影响,具有重要的经济和工程应用价值[3]。
常用的风速预测方法有时间序列法、持续法、卡尔曼滤波法、神经网络法、模糊理论、空间相关性法以及支持向量机法等[4-5]。其中,支持向量机(Support Vector Machine,SVM)采用结构风险最小化原则,解决了局部最小化问题,有较强的泛化能力和较好的非线性拟合能力,在风速预测中表现出优越的性能[6]。然而风速具有非平稳和非线性特征[7],使用SVM预测只能对风速的非线性部分进行较好的拟合,避免不了非平稳性对预测结果的影响。
综合风速序列的特性以及各种算法的优缺点,笔者提出一种经验模态分解(Empirical Mode Decomposition,EMD)、样本熵(Sample Entropy,SE)和支持向量机相结合的短期风速组合预测模型(Empirical Mode Decomposition,Sample Entropy and Support Vector Machines,EMD-SE-SVM)。
首先,为了降低风速非平稳性对预测结果的影响,采用EMD原理将风速序列逐级分解成不同尺度或趋势的子序列。子序列比原始序列的规律性更强,可以有效降低非平稳性的影响,提高预测精度[8]。
如果对EMD分解后得到的子序列一一进行建模预测,将会大大增加工作量,降低预测效率。因此,利用SE对各个子序列进行复杂度计算,将熵值相近的子序列归类叠加得到新的子序列,这样针对同一类序列建立相同的模型进行预测,将显著缩短预测时间。
此外,SVM模型的参数一般都需要根据经验人工试验选取,这要耗费大量的时间,也不能保证达到最好的效果,因此,笔者采用遗传算法(Genetic Algorithm,GA)来实现这些参数的自动选择寻优。
1 经验模态分解
EMD是一种基于信号局部特征的自适应信号分解方法。EMD将原始风速序列按不同尺度的波动或趋势逐级分解成若干个相互独立的固有模态分量(Intrinsic Mode Function,IMF),每个IMF须满足2个条件:①信号的零点数和极值数最多相差1个;②均值趋近于0。IMF比原始风速序列具有更强的规律性,有效地降低了非平稳性的影响[9]。
设风速序列为x(t),EMD分解步骤如下。
1)确定序列x(t)的极大和极小值。利用样条函数拟合序列的上、下包络线,计算上、下包络线的平均值m1。
2)考察x(t)与m1的差值h1是否满足IMF条件,满足则h1为首个IMF,不满足则将h1作为原始序列重复步骤1,直到重复k次步骤1后差值h1k(t)满足条件,称为一个IMF,记为c1(t)=h1k(t)。
3)从x(t)中分离出c1(t),得到剩余分量r1(t):
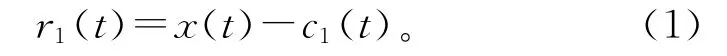
4)将r1(t)作为新的原始序列,重复步骤1~3,得出其余的n-1个IMF分量和1个余量,当余量rN(t)为单调函数时终止,原始信号经EMD分解后可以表示为

式中 cn(t)为IMF分量;rN(t)为余量。
2 样本熵
SE是时间序列复杂度的一种度量,序列越复杂熵值越大,利用这个特点可将SE值相近的IMF分量归为一类,提高风速预测效率。SE可用SampEn(N,m,r)表示,其中,N是数据长度,m是维数,r是相似容限。风速序列x(t)的SE计算步骤如下。
1)设x(t)为x(1),x(2),…,x(N)。将序列x(t)组成m维矢量:Um(i)=[x(i),x(i+1),…,x(i+m-1)],其中i=1,2,…,N-m。
2)定义dm(Um(i),Um(j))为Um(i)与Um(j)(j=1,2,…,N-m,且j≠i)中对应元素之差的最大值,即
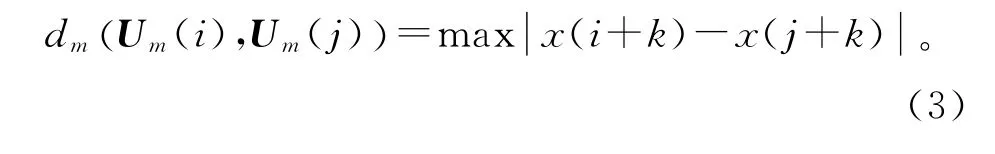
式中 k=0~m-1。对于每个i值都计算出dm(Um(i),Um(j))。



SE为

当N取有限值时,得到SE估计值:

SampEn的大小与m和r的值有关,一般取m=2,r=0.1~0.25SD,SD是风速序列x(t)的标准差,该文取m=2,r=0.2SD。
3 支持向量机
用于预测的SVM属于支持向量回归机(Support Vector Regress,SVR),主要有Vapnik提出的ε-SVR和Scholkopf等提出的ν-SVR[10]。笔者将采用ε-SVR对风速序列进行预测。

式中 ω为权值向量;b为偏置。其函数逼近问题等价于期望风险函数Rreg[f]最小,即
式中 Rreg[f]为期望风险;Remp[f]为经验风险,为常数。

利用结构风险最小化思想构造损失函数,通过求解约束条件的最优问题,可确定回归函数f(x),即


求解式(12)可得到支持向量机回归函数:

式中 k(Xi,X)为核函数,一般选取最常用的高斯核函数K(xi,xj)=exp(-‖xi-xj‖2/2σ2)。SVR预测的关键是获取ε,C和σ的最优取值组合。
笔者采用遗传算法来实现这些参数的自动选择,其优点是能自适应地调整搜索方向,不需要确定的规则,并且可以使所选取的参数具有一定的概率接受调整,避免陷入局部极小值而找到全局最优解,缩短参数寻优的时间,大大增加SVM预测模型的通用性。
4 基于EMD-SE-SVM的风速预测模型
笔者提出基于EMD-SE-SVM的短期风速预测模型的建模步骤。
1)对原始风速序列进行EMD分解,得到各子序列分量IMF(1~n)和余量rN(t)。
2)采用样本熵理论,对每一IMF信号分别进行复杂性评估。将样本熵值相近的IMF分量叠加起来作为一个新的序列输入SVM进行训练和预测。
3)对按样本熵分类叠加后得到的各子时间序列分别建立SVM预测模型进行预测,并利用遗传算法实现参数的自动选取和寻优,具体过程:
①将风速数据训练样本进行归一化预处理。
②参数初始化。设定参数范围C∈(0,106],ε∈[0,1],σ∈(0,2];遗传算法最大进化代数maxgen=200,种群最大数量sizepop=100,代沟ggap=0.9。
③利用遗传算法分别确定各序列的最优参数组合bestC,bestσ,bestε。
④利用归一化处理后的各序列风速数据训练样本和对应的最优参数组合训练出各自的支持向量机预测模型model。
4)将用于预测的各序列输入样本输入对应的预测模型model,得到各序列预测结果。最后,将各子序列的预测结果叠加得到风速预测结果,并与检验样本对比进行误差分析。
基于EMD-SE-SVM的风速预测流程如图1所示。

图1 基于EMD-SE-SVM的风速预测流程Figure 1 Flow chart of wind speed prediction based on EMD-SE-SVM
5 算例分析
笔者选取天津市某风电场风机2012年9月2—4日的实测风速数据为样本,采样间隔为10min,共432个采样点,采样得到的风速序列如图2所示。
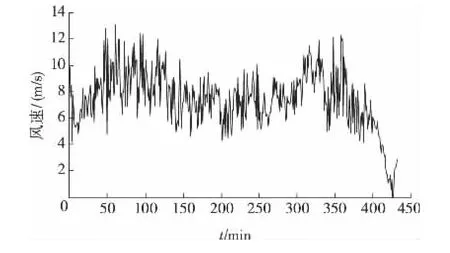
图2 原始风速序列Figure 2 The original sequence of wind speed
首先,按照文中1所述方法对原始风速序列进行经验模态分解,结果如图3所示,原始风速序列被分解成6个波动较小的分量IMF(1~6)和1个剩余分量r6。如果对这7个分量分别进行建模预测,将大大增加工作量,因此,按文中2所述方法对每个分量的复杂性进行评估,结果图4所示,可以看出,1,2号分量的样本熵值相近,3,4,5号分量的样本熵值相近,6,7号分量相近,将SE值相近的分量叠加作为一个新的子序列进行预测。依据SE值相近进行分类的结果如表1所示,叠加后得到的新子序列如图5所示,这样只需建立3个预测模型就能实现有效预测。
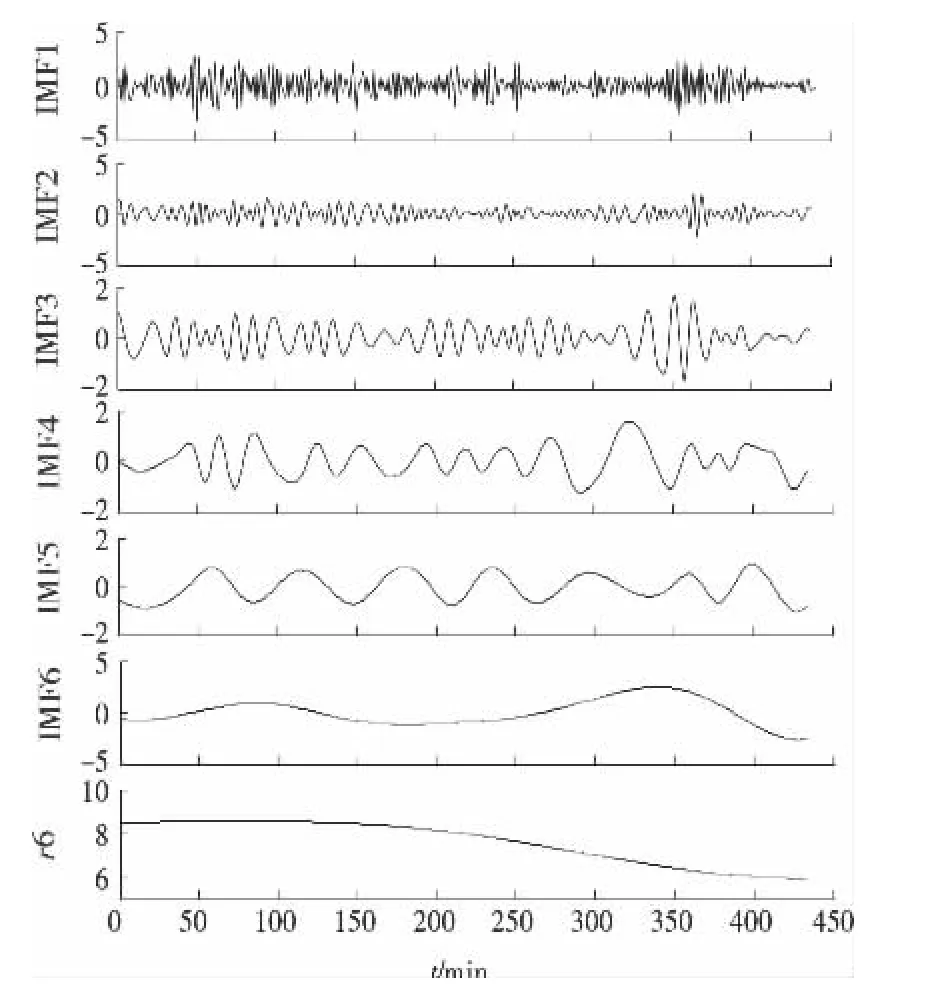
图3 EMD分解结果Figure 3 EMD Decomposition results

图4 各分量的SEFigure 4 SE for each component

表1 根据样本熵将各分量进行分类的结果Table 1 Classification results based on SE

图5 根据SE分类后的新子序列Figure 5 New subsequences classified by SE
对这3个子序列分别进行SVM建模预测。在一个子序列的432个采样点中,取前288个采样点为训练样本,后144个采样点为测试样本,进行提前一个时间点(10min)的风速预测。3个子序列的预测结果叠加后便得到原始风速序列的预测结果。采用该文遗传算法参数优化方法得到的各子序列SVM模型最优参数组合如表2所示。
为了对比验证该文提出方法的有效性,单独采用SVM方法对原始风速序列进行预测。EMD-SESVM方法和单一SVM方法的风速预测结果与实测数据对比如图6所示(由于有144个数据点,所以在4个小图中分段展示)。
为定量地评价各方法的预测结果与真实值接近程度,该文采用均方根误差(Root Mean Square Error,RMSE)和平均百分比误差(Mean Absolute Percentage Error,MAPE)2个评价指标,RMSE反映误差的离散程度,MAPE反映误差的总体水平。2个模型的误差比较如表3所示。

表2 各子序列SVM预测模型最优参数Table 2 Optimal parameters of SVM prediction model of each subsequence
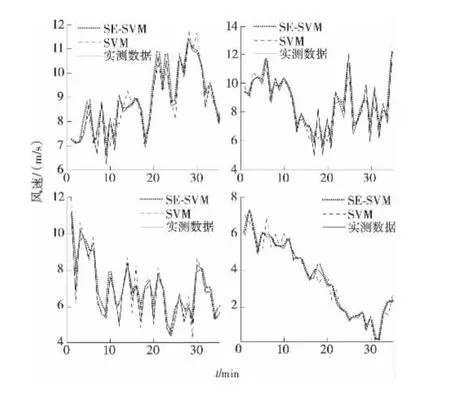
图6 未来10min风速预测值与实际值对比Figure 6 Comparison of forecasting and actual wind speed in the next 10mins

表3 EMD-SE-SVM与SVM的误差比较Table 3 Error comparison of EMD-SE-SVM and SVM
从图6和表3可以看出,与单纯使用SVM法相比,EMD-SE-SVM法的风速预测结果能更好地吻合实际值,预测结果的均方根误差和百分比误差比SVM分别降低了5.1%和5.4%,在风速波动较大的点附近,EMD-SE-SVM法对实际值的跟踪效果更好。这表明笔者提出的EMD-SE-SVM预测方法可以更充分地挖掘风速序列的特性,快速地对风速变化作出响应,有效地提高短期风速预测的准确度。
6 结语
1)笔者提出的EMD-SE-SVM短期风速预测模型可以将非线性非平稳的风速序列平稳化,准确把握各个尺度风速分量的变化规律。
2)根据样本熵复杂度分析理论,将多个风速序列进行分类,减少需预测模型的数量,提高预测效率。
3)算例研究表明,EMD-SE-SVM预测模型充分挖掘了风速序列的特性,能快速地对风速变化作出响应,预测结果的均方根误差和百分比误差分别比单纯采用支持向量机法降低了5.1%和5.4%,有效提高了短期风速预测的准确度。
[1]叶林,刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J].中国电机工程学报,2011,31(31):102-108.YE Lin,LIU Peng.Combined model based on EMDSVM for short-term wind power prediction[J].Proceedings of the CSEE,2011,31(31):102-108.
[2]马瑞,熊龙珠.综合考虑风电及负荷不确定性影响的电力系统经济调度[J].电力科学与技术学报,2012,27(3):41-46.MA Rui,XIONG Long-zhu.Power system economic dispatching considering the impact of wind powers and loads uncertainty[J].Journal of Electric Power Science and Technology,2012,27(3):41-46.
[3]王贺,胡志坚,张翌晖,等.基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测[J].电工技术学报,2014,29(4):237-245.WANG He,HU Zhi-jian,ZHANG Yi-hui,et al.A hybrid model for short-term wind speed forecasting based on ensemble empirical mode decomposition and least squares support vector machines[J].Transactions of China electro technical society,2014,29(4):237-245.
[4]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11):1-5.YANG Xiu-yuan,XIAO Yang,CHEN Shu-yong.Wind speed and generated power forecasting in wind farm[J].Proceedings of the CSEE,2005,25(11):1-5.
[5]鲁宗相,闵勇.基于功率预测的波动性能源发电的多时空尺度调度技术[J].电力科学与技术学报,2012,27(3):28-33.LU Zong-xiang,MIN Yong.Multiple time and spatial scale dispatching techniques of volatile energy generation based on power prediction[J].Journal of Electric Power Science and Technology,2012,27(3):28-33.
[6]鄢仁武,蔡金锭.FCM-HMM-SVM混合故障诊断模型及其在电力电子电路故障诊断中的应用[J].电力科学与技术学报,2010,25(2):61-67.YAN Ren-wu,CAI Jin-ding.FCM-HMM-SVM based mixed diagnostic model and its application in the power electronic circuit[J].Journal of Electric Power Science and Technology,2010,25(2):61-67.
[7]Liu H,Chen C,Tian H Q,et al.A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks[J].Renewable Energy,2012,48:545-556.
[8]刘志刚,王英,范福强.基于内禀模态奇异值伪熵特征提取的电能质量扰动识别[J].电力科学与技术学报,2013,28(2):3-9.LIU Zhi-gang,WANG Ying,FAN Fu-qiang.Power quality disturbances recognition based on feature extraction of empirical mode singular value pseudo entropy[J].Journal of Electric Power Science and Technology,2013,28(2):3-9.
[9]Huang N E,Shen Z,Long S R.The empirical modedecomposition and the Hilbert spectrum for nonlinear andnon-stationary time series analysis[J].Proceedings of TheRoyal Society Soc Lond,1998,454:903-995.
[10]Vapnik V N.The nature of statistical learning theory[M].New York:Springer-Verlag,2000.
[11]李瑾,刘金鹏,王建军.采用支持向量机和模拟退火算法的中长期负荷预测方法[J].中国电机工程学报,2011,31(16):63-66.LI Jin,LIU Jin-peng,WANG Jian-jun.Mid-long term load forecasting based on simulated annealing and SVM algorithm[J].Proceedings of the CSEE,2011,31(16):63-66.

