基于欠采样随机共振的单频微弱信号检测新方法*

石盛超，李广侠，李志强，冯少栋，张卫同

（1.解放军理工大学通信工程学院，南京210007;2.解放军96610部队，北京 102208）

基于欠采样随机共振的单频微弱信号检测新方法*

石盛超1，＊＊，李广侠1，李志强1，冯少栋2，张卫同1

（1.解放军理工大学通信工程学院，南京210007;2.解放军96610部队，北京 102208）

由于随机共振具有在特定条件下增强微弱信号信噪比的特性，近年来成为一种全新的微弱信号检测手段。为了克服随机共振绝热近似理论小参数条件的限制，提出一种基于欠采样随机共振的微弱信号检测方法。通过欠采样尺度变换与还原技术，实现了大参数信号的随机共振处理，突破了二次采样变尺度随机共振算法要求采样频率必须大于信号频率的50倍的限制。构建了基于欠采样随机共振的微弱信号检测模型，从理论上证明了方法的可行性。最后利用该方法对信噪比为－27 dB条件下的微弱单频信号检测进行了仿真，结果进一步验证了所提微弱信号检测方案的正确性。所提方法大大降低了信号的采样速率，为将随机共振应用于科斯塔斯（Costas）环的改进奠定了基础。

深空通信;微弱信号检测;随机共振;欠采样;尺度变换

1 引言

随机共振（Stochastic Resonance，SR）理论最初是由意大利学者 Benzi［1－2］等提出，用来解释地球远古气象中每隔10万年左右冰川期与暖气候周期交替出现的现象。随机共振理论指出:当淹没在强噪声背景中的微弱信号通过一个非线性系统时，如果非线性系统、信号与噪声达到某种匹配，会出现噪声增强信号的现象，从而提高输出端的信噪比。随机共振理论是本文研究的理论依据。

如何检测淹没在强噪声中的微弱信号一直是通信中亟需解决的问题，深空通信中更是面临极微弱信号接收的严峻挑战，常规的微弱信号检测方法［3－6］主要是基于时域和频域两种，有时域的相关方法、取样积分方法和频域的谱分析方法等。这些方法的共同点都是通过抑制噪声以提高信噪比，然而，当噪声频率与信号频率接近或重合时，抑制噪声的同时有用信号往往也不可避免地受到损害，这极大地影响了微弱信号的检测效果，成为微弱信号检测的瓶颈。深空通信中，点对点通信理论与技术得到了深入的研究，在应对低信噪比问题上也有众多的研究成果面世，并且很多技术已经被成功应用到各种深空探测任务中，得到了长足的发展。但是采用的一些方法和技术目前很难继续提高，无法应对未来深空探测的更高需求，因此，需要探讨新理论和新方法，通过新的思路解决未来深空通信面临的问题。

因此，寻找新的微弱信号接收方法以弥补传统方法的不足显得尤为重要。随机共振理论的提出给研究人员提供了新的微弱信号检测的思路［7］，其特有的噪声增强信号的特性打破了以往在微弱信号检测中必须抑制噪声来达到目标的观念，在对待噪声问题上，变为利用噪声来提高检测性能。但是，随机共振已有的绝热近似理论指出产生随机共振的信号条件是小参数（幅度、频率、噪声都小于1）信号，而实际的信号处理中应用的往往是大参数信号。为了克服绝热理论的限制，并且打破现有的二次采样随机共振变尺度算法［10］采样频率必须大于信号频率50倍的要求，拓宽随机共振理论在微弱信号检测领域的应用范围，本文提出一种基于欠采样的变尺度随机共振方法来实现对大参数微弱信号的检测，为随机共振理论在实际中的应用提供了新的思路和手段，结合弱残留载波辅助的传输架构，可以进一步将本文提出方法应用于深空通信当中，为解决深空通信中极微弱信号接收的瓶颈提供新的思路。

2 基于随机共振的微弱信号检测模型

2.1 双稳随机共振模型

随机共振系统3个必不可少的要素分别是非线性系统、输入信号和噪声，三者之间的关系如图1所示。

图1 随机共振原理框图Fig.1 Block diagram of stochastic resonance theory

在现有研究随机共振的理论中，应用最为广泛的是非线性双稳势阱模型，通常用朗之万微分方程来描述系统的数学特性，如式（1）所示:

2.2 欠采样随机共振单频微弱信号检测模型

当信号频率较大，超出绝热近似条件时，将不会发生随机共振现象。

为了克服这个限制，文献［8］提出了时序步进算法，通过设置合理的参数p和q，实现了信号从大参数到小参数的转变，进而实现随机共振。但是我们可以看到，当输入信号频率固定时，如果想要进行大参数信号的尺度变换，就必须要有一个目标小参数信号频率，而此时能够实现此操作的变换参数p和q可以有多种组合，在这些组合中寻找性能较好的参数设置是一个复杂繁琐的过程。基于以上考虑，本文提出一种固定单周期间隔的算法，大大降低了计算的复杂度，算法的具体思想是通过构建合适的采样频率对大参数信号进行欠采样，使欠采样之后的数据仍然构成周期信号，但是信号的频率将满足绝热近似条件，从而使得对欠采样信号进行处理可以发生随机共振现象，最后通过尺度反变换恢复原始信号特性。

基于以上的思路，提出基于欠采样的随机共振微弱信号检测模型的原理框图如图2所示。

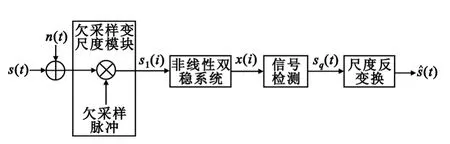
图2 欠采样随机共振微弱信号检测模型Fig.2 The model of weak signal detection based on under－sampling stochastic resonance

欠采样变尺度模块是整个检测模型的核心部分，通过选择合适的采样频率使欠采样之后的信号构成一个大周期慢变信号，实现大参数信号的变尺度转换，从而使欠采样信号频率满足绝热近似条件。

对满足绝热近似条件的欠采样信号进行随机共振处理，本文为了避免噪声调节随机共振的局限性，也为了更加接近实际系统，采用参数调节随机共振方法［11］，通过调节系统参数a和b来实现欠采样信号的随机共振。

欠采样信号经过非线性双稳系统的随机共振处理后，输出信号信噪比将得到有效的提升，但是由随机共振理论可知，输出信号的频率特性与非线性系统处理之前的欠采样信号保持一致。在信号检测模块中，本文采用的是频域微弱检测方法中常用的FFT频谱分析法对随机共振输出信号做频谱分析，实现对欠采样单频信号的恢复。

根据之前欠采样变尺度模块的处理系数，对信号检测模块恢复的信号进行尺度变换，从而得到整个系统输入信号的恢复信号。

3 基于欠采样的变尺度随机共振单频微弱信号检测算法

基于欠采样的变尺度随机共振单频微弱信号检测算法的核心思想是利用对信号进行欠采样来实现信号频率的尺度变换，大大降低了信号采样率，降低了处理的复杂度，并且应用范围更广，所受的限制条件更少，利于硬件实现。

假设输入的单频大参数周期信号频率为f，幅度为A，初始相位为 φ0，即

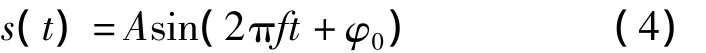
定义欠采样尺度变换系数为N，算法提出采样间隔如式（5）:

式（8）给出了输入信号频率f和欠采样信号频率fq之间的关系，是本文所提出算法的核心。

当输入信号f很大，超出绝热近似条件的情况下，可以通过选择合适的欠采样尺度变换系数N来对信号频率进行尺度变换，通过调整N来使fq满足绝热近似条件范围，从而可以对欠采样信号进行随机共振处理。

将欠采样之后的信号输入非线性双稳系统进行非线性处理，非线性处理的过程就是求解朗之万微分方程的过程，本文采用经典的四阶Runge－Kutta算法对式（1）进行求解，计算公式如式（10）:

其中，h为计算步长，a和b是前文提到的双稳势阱模型的系统参数，均为正值;s1（i）=s（i）+n（i）为欠采样序列和噪声序列之和，也就是非线性双稳系统的输入序列;通过四阶Runge－Kutta算法求解朗之万方程得到的非线性系统输出序列为x（i）。

随机共振理论指出，当信号、噪声和非线性系统三者协调产生随机共振现象时，非线性双稳系统的输出信号是一个类正弦信号，因此对应欠采样信号sq，非线性系统的输出信号可以表示为

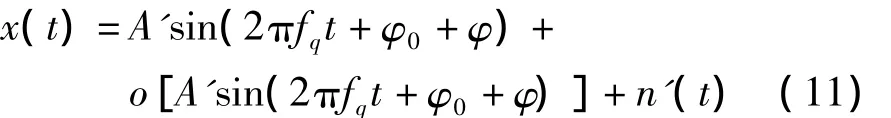
其中，A'为输出信号的幅值，φ为由于非线性处理时延而引入的相位差，o［A'sin（2πfqt+φ0+φ）］为比欠采样信号sq高阶的信号分量，n'（t）为非线性处理之后的噪声项。由于o［A'sin（2πfqt+φ0+φ）］的值非常小，因此输出信号可以近似为和输入的欠采样信号有着同样频率特性的单频信号，即

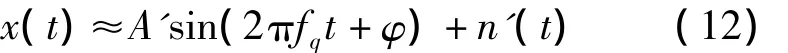
所以对输出信号x（t）做FFT频谱分析可以得到输入的欠采样信号的频率fq，并由式（8）给出的转换关系得到输入到基于欠采样随机共振微弱信号检测模型的信号频率

进而可以恢复出淹没在强噪声中的微弱的大参数单频信号，将信号幅值归一化，设置信号相位为零，得到最终恢复的信号如式（14）:

4 仿真结果

4.1 单频微弱信号检测仿真结果

本文选取信号频率f=2 000 Hz、信号幅值A=1的输入信号进行仿真分析。由于噪声为随机共振系统必需的组成要素之一，在整个随机共振处理中起着很重要的作用，首先要对信号加噪，本文采用最普遍的信噪比SNR作为衡量噪声强度的指标，在本文的仿真中设置SNR=－27 dB，输入信号和加噪之后的信号如图3所示。

图3 输入信号和加噪之后信号Fig.3 Input signal and signal jammed by noise

为了让欠采样信号频率fq满足绝热近似条件，本文选择尺度变换系数N=8 000，按照式（5）给出的采样间隔对加噪之后的输入信号进行欠采样，对欠采样得到信号做FFT频谱分析，得到的结果如图4所示，可以看到信号已经完全淹没在噪声中，无法分辨出欠采样之后信号的频率分量。

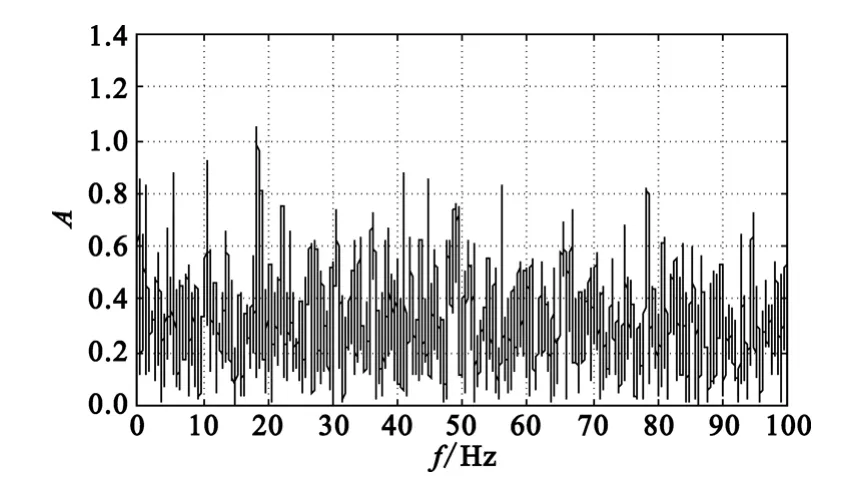
图4 欠采样信号频谱图Fig.4 Spectrum of under－ sampling signal

根据参数调节随机共振的结论，本文仿真时针对欠采样信号频率fq选取系统参数a=1，b=6.5，在利用四阶Runge－Kutta算法求解朗之万方程时，取计算步长为欠采样时间间隔，即h=Ts。输入非线性双稳随机共振模块前后的信号时域图如图5所示。

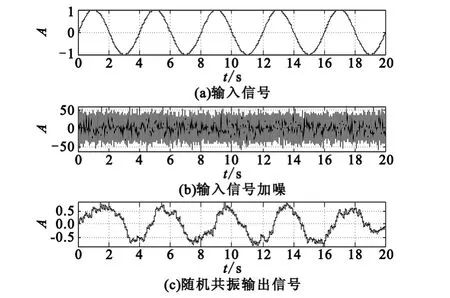
图5 随机共振处理时域图Fig.5 Time － domain diagram of stochastic resonance processing

从时域图的对比可以看出，欠采样信号已经能够满足绝热近似条件，经过非线性处理之后出现了明显的随机共振现象。经过随机共振处理之后的欠采样信号的周期特性已经非常明显。

对随机共振输出信号做FFT频谱分析，得到结果如图6所示。

图6 随机共振输出信号频谱图Fig.6 Spectrum of output signal

频谱特性呈现明显的单峰特性，已经接近单频信号的频谱特点，经过对欠采样随机共振输出信号的分析得到最大值处的频点fmax=0.250 3，由前文分析可知对应恢复的信号频率f=fmax×（N+1）=2 002.65，很好地实现了从强噪声中检测微弱信号的目标。

基于欠采样的变尺度随机共振算法，通过构建合适采样频率来对信号进行尺度变换从而使欠采样信号满足绝热近似条件，这样就可以对欠采样大参数信号进行随机共振处理，经过仿真验证出现了明显的随机共振现象，结合FFT频谱分析的方法有效检测出强噪声背景下的微弱信号。

4.2 性能分析

为了能够克服绝热近似理论的限制，拓宽随机共振的应用范围，很多学者都提出了相应的大参数变尺度随机共振算法，在众多的算法中，文献［10］提出的二次采样随机共振算法是应用最广泛的变尺度算法，但是在二次采样变尺度算法中，采样频率必须要超过信号频率的50倍，算法才能取得理想的效果，当信号频率本身就很大时，算法对采样率的要求使得系统复杂度提高，硬件实现也变得复杂，限制了二次采样算法的应用范围。

本文提出的欠采样变尺度随机共振算法采用的采样频率如式（6）所示，采样频率小于信号频率，可以看出本文提出的欠采样变尺度随机共振克服二次采样变尺度算法中对采样频率的要求，两者之间采样频率的对比如表1所示。

表1 两种变尺度算法的采样频率Table 1 The sampling frequency of two algorithms

仿真结果表明，本文提出的欠采样随机共振算法用于微弱信号检测取得了良好的效果，下面比较本文提出的算法与最佳线性滤波器（匹配滤波器）的微弱周期信号检测性能。欠采样随机共振微弱信号检测方法是否具有更好的信号检测性能关键要看随机共振输出信噪比能否大于最佳线性滤波器的输出信噪比。文献［12］指出，随机共振系统输出信噪比为

其中，σ2为噪声功率。而同样条件下最佳线性滤波器的输出信噪比是

按照前文仿真的条件，即 A=1，a=1，b=6.5，SNR=－27 dB。分别求出对应的输出信噪比为SNRout1= －17.4 dB，SNRout2= －22 dB。因此，本文提出的欠采样随机共振微弱信号检测方法性能明显优于最佳线性滤波器。

5 结论

本文提出的基于欠采样的随机共振算法解决了大参数信号不满足绝热近似条件而无法实现随机共振的问题，而且突破了二次采样随机共振变尺度算法要求采样频率必须大于信号频率50倍的限制，大大拓展了随机共振在信号处理中的应用领域，仿真结果表明可以很好地实现强噪声背景下微弱信号的有效检测。

本文所提方法不仅突破了随机共振中绝热近似理论小参数条件的限制，为微弱信号的检测提供了新的思路，还具有信号采样处理速率低、便于硬件实现的优点，具有十分广阔的应用前景，结合弱残留载波辅助的传输架构，可以进一步将本文提出方法应用于深空通信当中，作为解决深空通信中极微弱信号接收的新思路。

［1］Benzi R，Alfonso S，Vulpiani A.The mechanism of stochastic resonance［J］.Physical A，1981，14（11）:453 －457.

［2］Benzi R，Parisi G，Vulpiani A.Theory of Stochastic Resonance in Climatic Change［J］.IEEE Tellus，1983，43（3）:565－578.

［3］Williams C.Robust chaotic communications exploiting waveform diversity（part 1:Correlation detection and implicit coding）［J］.IET Communications，2008，2（10）:1213－1222.

［4］杨海博，王海燕，申晓红.奇异谱技术在混沌背景下微弱信号检测中的应用［J］.计算机测量与控制，2012，20（3）:593－595.

YANG Hai－ bo，WANG Hai－ yan，SHEN Xiao － hong.Singularity spectrum method for detecting weak signals under chaotic background［J］.Computer Measurement＆Control，2012，20（3）:593 －595.（in Chinese）

［5］刘磊，范铁生，王银斌，等.基于信号包络分析的并行微弱信号检测算法［J］.计算机应用，2012，32（8）:2133－2136.

LIU Lei，FAN Tie － sheng，WANG Yin － bin，et al.Paral-lel weak signal detection algorithm based on envelope analysis［J］.Journal of Computer Applications，2012，32（8）:2133 －2136.（in Chinese）

［6］夏均忠，刘远宏，冷永刚，等.微弱信号检测方法的现状分析［J］.噪声与振动控制，2011，31（3）:156 －161.

XIA Jun － zhong，LIU Yuan － hong，LENG Yong － gang，et al.Analysis of methods of weak signal detection［J］.Noise and Vibration Control，2011，31（3）:156 － 161.（in Chinese）

［7］蔡卫菊.基于随机共振的微弱信号检测［J］.信息与电子工程，2012，10（2）:210 －212，236.

CAI Wei－ju.Detecting weak signal based on stochastic resonance［J］.Information and Electronic Engineering，2012，10（2）:210 －212，236.（in Chinese）

［8］张宇，赵远，唐勐，等.随机共振应用于大频率周期性弱信号检测［J］.哈尔滨工业大学学报，2008，40（11）:1793－1795.

ZHANG Yu，ZHAO Yuan，TANG Meng，et al.Detection of high frequency periodic weak signal based on stochastic resonance［J］.Journal of Harbin Institute of Technology，2008，40（11）:1793 －1795.（in Chinese）

［9］Mcnamara B，Wiesenfeld K，Roy R.Observation of stochastic resonance in a ring laser［J］.Physical Review Letters，1988，60（25）:2626 －2629.

［10］冷永刚，王太勇.二次采样用于随机共振从强噪声中提取弱信号的数值研究［J］.物理学报，2003，52（10）:2432－2437.

LENG Yong－gang，WANG Tai－yong.Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise［J］.Acta Physica Sinica，2003，52（10）:2432 －2437.（in Chinese）

［11］XU Bo － hou，Duan F，Bao R，et al.Stochastic resonance with tuning system parameters:The application of bistable systems in signal processing［J］.Chaos，Solitons and Fractal，2002，13（4）:633 － 644.

［12］杨定新.微弱特征信号检测的随机共振方法与应用研究［D］.长沙:国防科学技术大学，2004.

YANG Ding－xin.On Methodology and Application of Weak Characteristic Signal Detection Based on Stochastic Resonance［D］.Changsha:National University of Defense Technology，2004.（in Chinese）

A Novel W eak Single Frequency Signal Detection M ethod Based on Under－Samp ling Stochastic Resonance

SHI Sheng －chao1，LI Guang －xia1，LI Zhi－qiang1，FENG Shao －dong2，ZHANG Wei－tong1
（1.College of Communications Engineering，PLA University of Science and Technology，Nanjing 210007，China;2.Unit 96610 of PLA，Beijing 102208，China）

Stochastic resonance is widely applied to detect weak signal in a strong noise background because it can enhance the signal－to－noise ratio（SNR）.A weak single frequency signal detection method based on under－sampling stochastic resonance is proposed to solve the problem that traditional stochastic resonance can be only applied to deal with small parameter signals.Stochastic resonance is successfully expanded into the applications of the large parameter signals on the basis of scale－transformation and retrieve technology in the under－ sampling stochastic resonance.Moreover，the algorithm overcomes the limit that signal frequency must be more than 50 times of the sampling frequency in the second sample algorithm.The model of weak signal detection based on under－sampling stochastic resonance is put forward.Finally，detecting the weak single frequency signal under SNR= －27 dB background by the method proposed in this paper is simulated.The result proves the validity of the method.The sampling frequency in the method is much less than that in the traditional methods and this is helpful to apply stochastic resonance in improving the performance of the Costas loop.

deep space communication;weak signal detection;stochastic resonance;under－sampling;scale transformation

The National Natural Science Foundation of China（No.61032004，91338201）;The National High Technology Research and Development Program of China（863 Program）（2012AA121605，2012AA01A503，2012AA01A510）

＊＊

shishengchao@126.com Corresponding author:shishengchao@126.com

TN911.72

A

1001－893X（2014）05－0605－06

10.3969/j.issn.1001 －893x.2014.05.015

石盛超，李广侠，李志强，等.基于欠采样随机共振的单频微弱信号检测新方法［J］.电讯技术，2014，54（5）:605－610.［SHI Shengchao，LI Guang － xia，LI Zhi－ qiang，et al.A Novel Weak Single Frequency Signal Detection Method Based on Under－ Sampling Stochastic Resonance［J］.Telecommunication Engineering，2014，54（5）:605 － 610.］

2013－10－30;

2014－03－24

date:2013－10－30;Revised date:2014－03－24

国家自然科学基金资助项目（61032004，91338201）;国家高技术研究发展计划（863计划）项目（2012AA121605，2012AA01A503，2012AA01A510）

石盛超（1988—），男，山东即墨人，2011年于解放军理工大学获工学学士学位，现为硕士研究生，主要研究方向为卫星通信、卫星测控。

SHI Sheng－ chao was born in Jimo，Shandong Province，in 1988.He received the B.S.degree from PLA University of Science andTechnology in 2001.He is now a graduate student.His research concerns satellite communications and satellite TT＆C.

Email:shishengchao@126.com