修正的干扰噪声自相关矩阵重构波束形成算法*

丛凤翔，王 伟，魏东兴

（1.大连理工大学信息与通信工程学院，辽宁大连116024;2.解放军66440部队，石家庄 050081）

修正的干扰噪声自相关矩阵重构波束形成算法*

丛凤翔1，＊＊，王 伟2，魏东兴1

（1.大连理工大学信息与通信工程学院，辽宁大连116024;2.解放军66440部队，石家庄 050081）

为改善采样自相关矩阵求逆（SMI）算法中期望信号存在于接收信号所引起的性能下降，提出一种修正干扰噪声自相关矩阵重构（CMR）算法。该算法首先选取采样自相关矩阵特征分解的最小特征值对应的特征向量构造空间分布系数，再对其在非期望信号波达方向上进行累加实现矩阵的重构。当存在相干信号时，可采取先利用特征向量元素对协方差矩阵进行托普利兹化处理实现解相干，再进行矩阵重构的托普利兹矩阵重构（TCMR）算法。计算机仿真与实验结果证明适用于非相干信号条件下的CMR算法与适用于相干信号条件下的TCMR算法具有更好的输出性能。

波束形成;特征空间分解;自相关矩阵重构;相干信号;托普利兹矩阵

1 引言

波束形成算法是阵列信号处理领域的主要研究内容，在雷达、声纳、地震勘测以及移动通信领域得到了迅速发展和广泛应用［1］，算法按类别可以分为利用信号先验知识的盲波束形成算法以及需要导频信号或波达方向角（Direction of Arrival，DOA）的非盲算法［2］。当期望信号的DOA可估计时，SMI算法是最常用的算法之一，该算法在足够多的采样点数下可以获得良好的输出性能［2］。近年来出现了多种SMI算法的改进算法，如抑制小特征值扰动的对角载入（Diagonal Loading，DL）类算法［3－4］、可以提升算法鲁棒性的基于特征空间（Eigen Space Based，ESB）类算法［5］、可以对阵列方向图旁瓣进行有效控制的稀疏矩阵约束算法［6］、二次型约束算法［7］，以及能够减弱采样信号中期望信号对系统影响的干扰噪声自相关矩阵重构类算法［8－10］。文献［8］中的矩阵重构算法需要准确知道全部干扰信号的DOA，而文献［9］与［10］中的算法需要对期望信号的方向向量进行约束。

本文运用累加空间分布系数的思想，提出了直接利用最小特征向量重构干扰噪声自相关矩阵的自相关矩阵重构（Covariance Matrix Reconstruction，CMR）算法，具有更强的干扰抑制性能。在相干信号干扰条件下，本文对文献［11］与［12］中的解相干技术进行了改进，用该技术对协方差矩阵进行托普利兹化处理后再运用CMR算法（Toeplitz CMR，TCMR），从而有效地抑制相干信号波达方向上的干扰。CMR与TCMR两种算法适用于期望信号信噪比（Signal－to－Noise Ratio，SNR）与干扰信号干噪比（Interference－to－Noise Ratio，INR）较高的实际应用中，可以获得良好的输出性能。

2 信号模型

3 重构干扰噪声自相关矩阵的波束形成算法

本节在上述阵列模型基础上，对适用于非相干信号环境下的CMR算法与相干信号环境下的TCMR算法进行了推导与分析。

3.1 非相干信号环境下的矩阵重构算法

3.2 相干信号环境下的矩阵重构算法

由于传播环境的复杂性，入射到阵列的信号中常含同频干扰以及多径传播信号等相干信号，导致信源协方差矩阵的秩亏损，使CMR算法无法在相干信号波达方向上形成有效的零陷，因此TCMR算法首先对接收信号的协方差矩阵进行解相干处理。

相干信号的存在所引起的秩亏损将导致矩阵的大特征值数目降低，当全部入射信号为相干信号时，自相关矩阵的秩降到最小值1。因此，当式（11）中的ei取对应于最大特征值的特征向量emax时恒成立，故emax可以看作包含所有入射信号信息的线性组合。

为解决秩亏损问题，更有效地利用数据信息，对阵列接收协方差矩阵Rxx进行特征分解前将其与反向协方差矩阵进行平均:

4 实验结果与性能分析

本节分别于不存在与存在相干信号两种条件下对CMR算法、TCMR算法与 SMI算法、DL算法、ESB算法等传统算法的性能进行计算机仿真，并在DSP开发平台上对TCMR算法与SMI算法的运算时间与资源消耗进行监测对比。实验中信号的数据模型为先后经过127位扩频码扩频与16QAM调制的20 000个二进制原始数据，再被调制到32个OFDM子载波上，经过高斯白噪声信道后入射到10阵元均匀线阵上。

4.1 非相干信号环境下的性能仿真

对CMR算法与另外3种算法的阵列方向图进行仿真。期望信号与3组干扰信号分别从－20°、－40°、20°和 40°入射，期望信号的输入 SNR 为10 dB，INR为30 dB，信号采样点数 K为200，CMR算法在区间上每隔1°取一个采样角度，DL算法中对角加载因子ξ=10σ2n，仿真结果如图1所示。虽然CMR算法的主瓣被一定程度地展宽，但在干扰信号波达方向上可以形成较深的零陷。当干扰信号的INR较大时，可以更有效地抑制干扰信号，获得良好的输出性能。CMR算法有较低的旁瓣电平，可以有效降低旁瓣方向上的噪声分量，进一步优化系统性能。

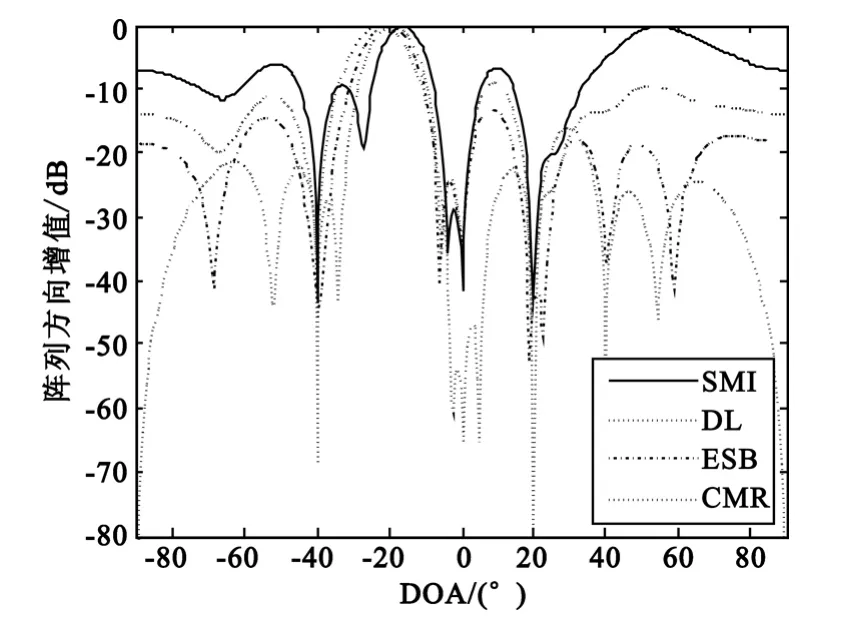
图1 不同算法的阵列方向图Fig.1 Beam pattern of different algorithms

相同期望信号SNR条件下输出SINR的大小是衡量波束形成算法性能最常用的方式之一。当干扰信号 INR固定为30 dB时，期望信号的 SNR从－10 dB至35 dB变化时不同算法经过200次蒙特卡罗仿真后的输出SINR曲线以及（SINR）opt曲线如图2所示。在该实验条件下，当SNR＞5 dB时ESB等传统改进算法的输出SINR不再线性增加。由于CMR算法在选取累加区间时移除了期望信号的可能到达方向，有效克服了期望信号SNR较高条件下对系统性能的影响，使CMR算法曲线近似于线性关系，输出性能接近（SINR）opt。CMR算法对SMI算法等传统算法性能的改善随着SNR的增大而增大，因此在高SNR条件下其优越性更为突出。

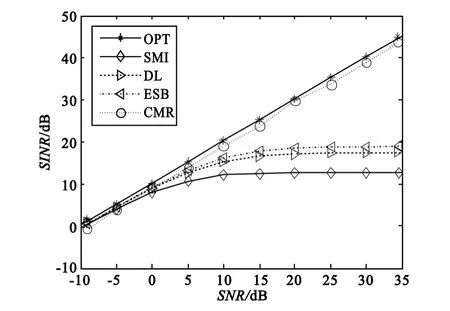
图2 非相干信号环境下输出SINR与SNR的关系曲线Fig.2 Output SINR versus SNR curves under incoherent signal circumstance

4.2 相干信号环境下的性能仿真

期望信号的波达方向角仍为20°，3组INR为15 dB的相干信号分别从40°、－20°和 －40°入射到10阵元均匀线阵。TCMR算法、CMR算法与传统算法在不同SNR条件下的输出SINR曲线与（SINR）opt曲线的蒙特卡罗仿真结果如图3所示。当存在相干信号干扰时，CMR算法在高信噪比的条件下输出性能总体上优于SMI算法与ESB算法，但输出曲线不稳定。对矩阵的Toeplitz化处理使TCMR算法具有良好的相干干扰抑制能力，在高信噪比条件下随着SNR的升高仍然具有稳定且接近（SINR）opt的线性曲线。

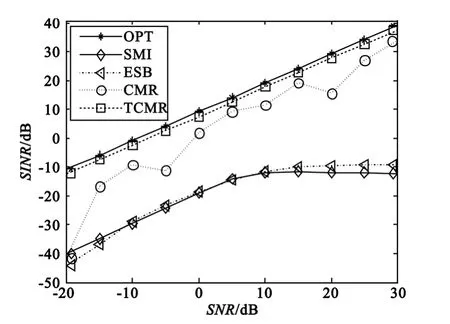
图3 相干信号环境下输出SINR与SNR的关系曲线Fig.3 Output SINR versus SNR curves under coherent signal circumstance

4.3 不同算法硬件实现的资源消耗

本实验在配备主频为300 MHz的芯片TMS320C6747的 DSP开发平台上进行，并具有256 MB的SDRAM，有较大的存储空间用于数据处理。实验对比了TCMR算法与SMI算法在期望信号取不同SNR时的误码率（Bit Error Rate，BER）。几组信号的波达方向与4.2节相同，采样点数K取200，INR=15 dB。监测软件记录的两种算法在权值计算过程中消耗的时间与存储空间如表1所示，计算误码率并导出至计算机绘制BER与SNR的关系曲线如图4所示。

表1 权值计算时的CPU时钟数与存储空间消耗Table 1 Calculation consumption of total CPU cycles and heap resources

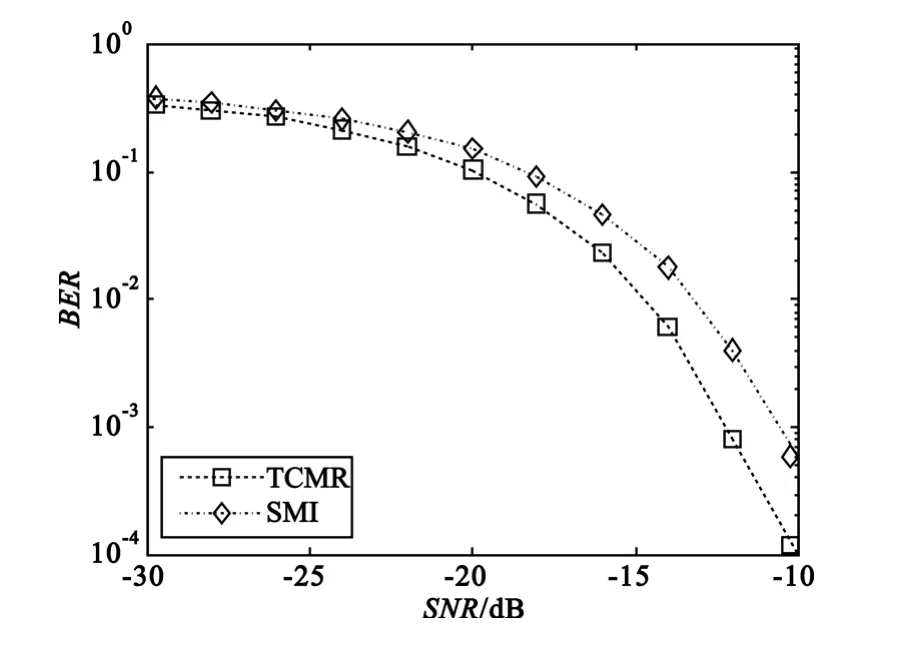
图4 BER与SNR的关系曲线Fig.4 BER versus SNR curves

从图4可以看出，在相同SNR条件下TCMR算法可以获得较低的BER，在高SNR条件下算法的优越性更为明显。在该实验条件下，当期望信号的SNR大于－10 dB时TCMR算法能够使BER下降至10－4以下。表1中，算法运算时间用消耗的CPU时钟数表示，消耗的存储空间用与天线阵元数M有关的式子表示。由于TCMR算法需要进行特征分解与空间分布系数累加，增加了运算时间与空间消耗。但在资源充足以及实时性要求不是非常高的条件下，可以以此为代价换取输出性能的提高与BER的下降。

5 结束语

针对SMI算法中阵列接收信号中存在期望信号所引起的系统性能下降，本文介绍了分别适用于非相干信号条件下的CMR算法与相干信号条件下的TCMR算法。算法主要利用空间分布系数在非期望信号波达方向上的累加来消除高SNR的期望信号对系统性能的影响。TCMR算法在此基础上通过构造Toeplitz化矩阵的方式使算法能够有效抑制相干信号干扰。计算机仿真与硬件实验结果证明了CMR算法与TCMR算法具有良好的输出性能。算法在非期望信号方向上累加分布系数增大了对存储空间的要求，该过程与TCMR算法需要进行的二次特征分解增加了算法的运算量，后续工作应当从减少运算量的角度进行深入研究，以扩展算法的应用范围。

［1］ 张贤达，保铮.通信信号处理［M］.北京:国防工业出版社，2000.

ZHANG Xian － da，BAO Zheng.Modern signal processing［M］.Beijing:National Defense Industry Press，2002.（in Chinese）

［2］Cox H，Zeskind R M，Oven M H.Robust adaptive beamforming［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，35（10）:1365 －1376.

［3］Carlson B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays［J］.IEEE Transactions on Aerospace and Electronic Systems，1988，24（4）:397 －401.

［4］Elnashar A，Elnoubi S M，El－Mikati H A.Further study on robust adaptive beamforming with optimum diagonal loading［J］.IEEE Transactions on Antennas and Propagation，2006，54（12）:3647 －3658.

［5］Jung－Lang Y，Yeh C C.Generalized eigenspace－based beamformers［J］.IEEE Transactions on Signal Processing，1995，43（11）:2453 －2461.

［6］Liu Y，Wan Q.Robust beamformer based on total variation minimisation and sparse － constraint［J］.Electronics Letters，2010，46（25）:1697 －1699.

［7］Nai S － E，Ser W，Yu Z － L，et al.A robust adaptive beamforming framework with beampattern shaping constraints［J］.IEEE Transactions on Antennas and Propagation，2009，57（7）:2198 －2203.

［8］Mallipeddi R，Lie J P，Razul S G，et al.Robust adaptive beamforming based on covariance matrix Reconstruction for look direction mismatch［J］.Progress in Electromagnetics Research Letters，2011，25:37 －46.

［9］GU Yu － jie，Leshem A.Robust adaptive beamforming based on interference covariance matrix Reconstruction and steering vector estimation［J］.IEEE Transactions on Signal Processing，2012，60（7）:3881 －3885.

［10］Lu Z，Li Y，Gao M，et al.Interference covariance matrix Reconstruction via steering vectors estimation for robust adaptive beamforming［J］.Electronics Letters，2013，49（22）:1373－1374.

［11］Yang－Ho C.ESPRIT－Based coherent source localization with forward and backward vectors［J］.IEEE Transactions on Signal Processing，2010，58（12）:6416 －6420.

［12］Zhang Jie，Huang Deng － shan，Huang Ping，et al.Estimation DOAs of the coherent sources based on SVD［C］//Proceedings of 2010 2nd International Conference on Signal Processing Systems（ICSPS）.Dalian:IEEE，2010:174－177.

A M odified Interference－p lus－noise Covariance M atrix Reconstruction Algorithm for Beam former

CONG Feng － xiang1，WANG Wei2，WEI Dong － xing1
（1.School of Information and Communication Engineering，Dalian University of Technology，Dalian 116024，China;2.Unit 66440 of PLA，Shijiazhuang 050081，China）

To improve the performance reduction of sample matrix inversion（SMI）algorithm as the desired signal exists in training data，a modified interference－plus－noise covariance matrix reconstructing（CMR）algorithm is proposed in this paper.The algorithm firstly uses the eigenvector corresponding to the minimum eigenvalue of the sample autocovariance matrix to structure the space distribution coefficient，and then accumulates it on the range except the direction of the desired signal to reconstruct the interference－plus－ noise covariance matrix.In the presence of coherent signals，the element in the max eigenvector can be utilized to make the covariance matrix a Toeplitz matrix，and then the CMR algorithm（Toeplitz CMR，TCMR）can be used.Simulation and experiment results demonstrate that the CMR algorithm applied in incoherent signal circumstance and the TCMR algorithm applied in coherent signal circumstance have better output performance.

adaptive beamforming;eigenspace decomposition;covariance matrix reconstruction;coherent signals;Toeplitz matrix

TN911.7

A

1001－893X（2014）05－0584－05

10.3969/j.issn.1001 －893x.2014.05.011

丛凤翔，王伟，魏东兴.修正的干扰噪声自相关矩阵重构波束形成算法［J］.电讯技术，2014，54（5）:584－588.［CONG Feng－xiang，WANG Wei，WEI Dong － xing.A Modified Interference － plus－ noise Covariance Matrix Reconstruction Algorithm for Beamformer［J］.Telecommunication Engineering，2014，54（5）:584 －588.］

2013－12－09;

2014－02－26

date:2013－12－09;Revised date:2014－02－26

＊＊

congfengxiang@163.com Corresponding author:congfengxiang@163.com

丛凤翔（1988—），男，河北石家庄人，2011年获学士学位，现为硕士研究生，主要研究方向为阵列信号处理;

CONG Feng－xiang was born in Shijiazhuang，Hebei Province，in 1988.He received the B.S.degree in 2011.He is now a graduate student.His research direction is array signal processing.

Email:congfengxiang@163.com

王 伟（1981—），男，河北昌黎人，2011年获硕士学位，现为工程师，主要研究方向为无线通信技术;

WANG Wei was born in Changli，Hebei Province，in 1981.He received the M.S.degree in 2011.He is now an engineer.His research concerns wireless communication technology.

Email:wangqisong2380@sina.com

魏东兴（1969—），男，辽宁大连人，1994年获硕士学位，现为副教授，主要研究方向为宽带通信理论及应用、移动通信、无线通信技术。

WEI Dong － xing was born in Dalian，Liaoning Province，in 1969.He received the M.S.degree in 1994.He is now an associate professor.His research concerns broadband communication theory and application，mobile communication and wireless communication technology.

Email:weidx@dlut.edu.cn