四面受热时型钢混凝土柱的简化计算方法研究
王玉镯,范安宁,闫凯,傅传国
(山东建筑大学 土木工程学院,山东 济南250101)
0 引言
型钢混凝土结构是将型钢与混凝土相结合的一种组合结构,具有承载力大、塑性好等优点,因而被广泛用于高层和超高层建筑中。随着我国建筑行业的快速发展,火灾在建筑结构中发生的频率也日益提高,对国民经济和人类环境造成了巨大的损失和破坏。因此,研究型钢混凝土结构的抗火性能逐渐成为人们关注的热点。
目前,国内外学者分别对火灾中、火灾后的结构本身所用材料和结构的力学性能进行了试验研究和理论分析,取得了大量的理论成果和试验数据[1-3]。有学者对型钢混凝土柱开展了试验研究和有限元分析[4-5],给出了型钢混凝土柱耐火极限的计算公式,并为规程所采用。参考常温下型钢混凝土柱承载能力的计算公式,并借鉴高温下钢筋和混凝土的本构关系,推导了高温下型钢混凝土柱承载能力的计算公式,为工程实际应用提供参考。
依据已有的试验研究[1-2],分析常温下型钢混凝土柱的承载力可知:火灾中型钢混凝土柱的破坏特点与常温下的破坏模式类似,故高温下型钢混凝土柱采用如下假设:
(1)平截面假定;
(2)忽略混凝土的收缩和徐变;
(3)只考虑钢材的抗拉强度;
(4)钢材强度取其设计值,不大于屈服强度;
(5)由于型钢所占的面积较大,取混凝土的净截面计算。
1 高温下材料的简化力学模型
1.1 高温下混凝土的抗压强度
混凝土的高温抗压强度fTc随温度T变化的曲线[2],如图1(a)所示。其简化计算模型如图1(b)所示,根据简化的曲线模型,得到其计算式(1)为


图1 混凝土的温度—抗压强度曲线图(a)高温下混凝土的强度—温度关系图;(b)混凝土的简化计算高温强度图
1.2 高温下钢筋的抗拉强度
高温下钢材的抗拉强度fTy与温度T变化的曲线[2],如图2(a)所示。其简化计算模型如图2(b)所示,根据简化的曲线模型,得到其计算式(2)为式中为高温下钢筋的强度设计值,N/mm2;fy为常温下钢筋的强度设计值,N/mm2。

2 高温下型钢混凝土柱的有限元分析
2.1 高温下型钢混凝土柱的等效截面
利用有限元软件ABAQUS,对截面尺寸为300 mm×300mm型钢混凝土柱进行了四面受火模拟[6],采用ISO—834标准升温曲线,获得了柱截面的温度场分布情况(如图3所示),从而可以简化出300、800℃ 等温线的具体位置,如图 4(a)、(b)、(c)、(d)所示。按照截面极限承载力的等效原则和高温下钢筋和混凝土的强度曲线,对300、800℃等温线的位置近似简化,即得相应的等效截面位置,即型钢混凝土柱截面简化如图5所示。

图2 钢筋的温度—强度曲线图(a)高温下钢筋的温度—强度关系图;(b)钢筋的简化计算高温强度图

图3 柱四面受火温度场图
通过有限元软件对大量不同截面尺寸的温度场计算,根据已知的构件尺寸及耐火极限,从而可以确定300℃(T3)等温线和800℃(T8)等温线的具体位置。
当耐火极限 t=60 min时,300℃(T3)和800℃(T8)等温线的位置可由式(3)、(4)计算为
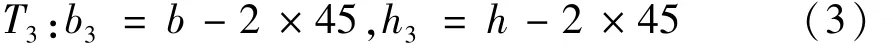
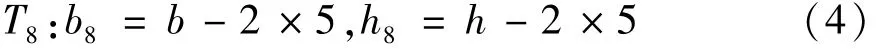
当耐火极限t=90 min时,T3和T8等温线的位置可由式(5)、(6)计算为

当耐火极限t=120 min时,T3和T8等温线的位置可由式(7)、(8)计算为
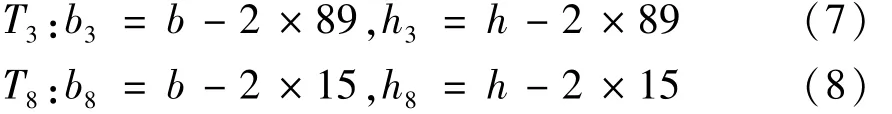
当耐火极限t=180 min时,T3和T8等温线的位置可由式(9)、(10)计算为

式中:b3、b8分别为300、800℃等温线的柱截面宽度,mm;h3、h8分别为300、800℃等温线的柱截面高度,mm;b为柱截面宽度,mm;h为柱截面高度,mm。

图4 不同时间柱四面受火等温线图(a)60 min;(b)90 min;(c)120 min;(d)180 min

图5 柱四面受火等效截面图
2.2 型钢混凝土柱正截面承载力计算
根据以上假定和确定的等效截面,其计算简图如图6(a)、(b)所示,根据截面的平衡原理建立了高温下型钢混凝土柱正截面偏心受压承载力的计算式(11)~(16)[7-10]。
由平衡条件可得:

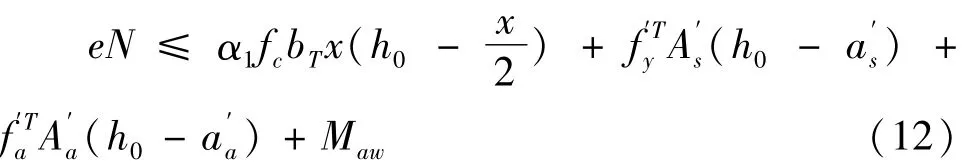
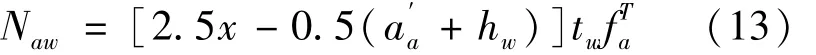
腹板承担的弯矩为
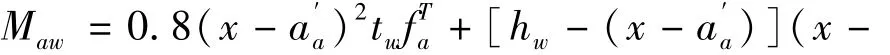


腹板承担的弯矩为
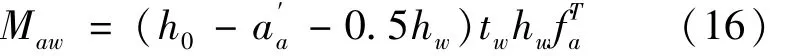
腹板的轴向承载力为的宽度,mm;hw为腹板的截面高度,mm;M为高温下构件的弯矩设计值,N·m;Maw为构件中型钢腹板承受的弯矩,N·m;Naw为构件中型钢腹板承受的轴力为高温下钢筋采用的强度设计值,取值不大于其屈服强度为高温下型钢受拉区、受压区采用的强度设计值,取值不大于其屈服强度;为受拉区钢筋、受压区钢筋的面积,mm2;Aa、为型钢的受拉、受压翼缘的计算截面面积,mm2;为型钢的受拉、受压腹板边缘到截面最近边的距离,mm。

图6 柱截面承载力计算简图(a)截面应力平衡图;(b)等效应力分布图
2.3 算例验证
对型钢混凝土柱高温下的极限载力做了一些试验性的研究[11],其型钢混凝土矩形柱的截面如图7所示,柱高1540 mm,截面尺寸250 mm×250 mm,Q345热轧H型钢,纵向主筋为4根12 mm的热轧钢筋,混凝土的等级为C30,钢筋的混凝土保护层厚度为25 mm,纵筋和箍筋均采用HRB335级钢筋,设计轴力N=700 kN,弯矩设计值M=70 kN·m在火灾作用下,耐火极限取90 min,验算该柱的承载力。
为了同试验结果进行比较,截面参数和材料强度与实际试验中的取值一致:fc=24 N/mm2,fTa=152 N/mm2,fTy=187 N/mm2,l0=1540mm,bT=hT=200 mm,按照式(11)和式(12)计算得:计算值N=865 kN,其值大于设计值N=700 kN,而计算值M=132 kN·m大于设计值M=70 kN·m,均满足承载力的要求,该型钢混凝土柱在火灾作用下,耐火极限为90 min的要求下,柱的截面强度满足要求。
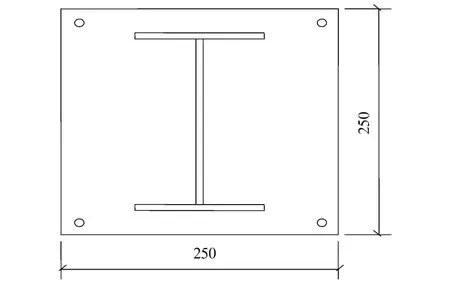
图7 型钢混凝土矩形柱截面示意图
对相同截面尺寸和设计参数的型钢混凝土柱在火灾作用下的剩余承载力和破坏 形态进行了试验研究[11],上述算例与实验中的设计参数均相同,柱在火灾下承受弯矩和轴力的共同作用,实验中的最大强度为N=886 kN、M=124 kN·m,经比较,试验轴力值与计算结果相接近,计算弯矩值大于试验弯矩值。由于试验过程中存在型钢混凝土柱初始偏心,试验误差和材料的不均匀性等因素,从而使轴向承载力的试验值略低于理论计算值。由此可见,利用文中公式计算的理论值与试验值具有一定的吻合度,从而说明公式的合理性,为在实际中采用提供依据。
3 结论
通过本研究可知:
(1)在对高温下材料的力学性能曲线进行合理简化的基础上,根据等效截面原理,建立了高温下型钢混凝土柱正截面受压承载力的计算公式。(2)计算所得的型钢混凝土柱的弯矩值为865 kN,轴力值为132 kN·m,与其试验值具有一定的吻合度。该公式具有一定的合理性和可操作性,为实际工程中考虑高温作用并进行型钢混凝土柱的抗火性能设计提供理论参考依据。
[1] 过镇海,时旭东.钢筋混凝土的高温性能及其计算[M].北京:清华大学出版社,2002.
[2] 吴波.火灾后钢筋混凝土结构的力学性能[M].北京:科学出版社,2003.
[3] 王玉镯.火灾作用下(后)混凝土框架节点的力学性能分析[D].南京:东南大学,2010.
[4] 韩林海,郑永乾.SRC柱和RC柱的耐火性能及抗火设计方[C].第三届全国钢结构防火及防腐技术研讨会暨第一届全国结构抗火学术交流会论文集.福州:福大高校出版社,2005.
[5] 宋天诣,韩林海,经建生.型钢混凝土柱耐火性能的试验研究[C].第四届全国钢结构防火防腐技术研讨会暨第二届全国结构抗火学术交流会论文集.上海:同济大学出版社,2007.
[6] 傅传国,王广勇,王玉镯.火灾下钢筋混凝土框架节点温度场分析[J].山东建筑大学学报,2009,24(1):1-8.
[7] 傅传国,于德帅,傅煜晨,等.预应力型钢混凝土梁火灾下抗弯承载算[J].山东建筑大学学报,2013,28(3):189-196.
[8] 王玉镯,傅传国,韩月臻,等.火灾影响下钢筋凝土单向板的计算方法[J].山东建筑大学学报,2006,21(6):480-482.
[9] 王玉镯,傅传国.ABAQUS结构工程分析及实例详解[M].北京:中国建筑工业出版社,2010.
[10]傅传国,王玉镯,于德帅.火灾作用下预应力型钢混凝土简支梁承载性能试验研究[J].自然灾害学报,2012,32(1):1-7.
[11]李俊华,唐跃峰,刘明哲.火灾后型钢混凝土柱受力性能试验研究[J].建筑结构学报,2012,33(2):56-63.

