基于改进粒子群算法优化的水轮机组低频振荡PID控制研究

钱 涛

（苏州工业职业技术学院电子与通信工程系，江苏 苏州，215104）

0 前言

水轮机能够将水流的能量转换为机械能，属于一种透平式流体机械，主要应用于水电站内，可以驱动发电机发电。低频振荡导致电网不稳定运行的主要问题，已经得到了广泛关注，电网系统低频振荡频率范围为0.5～2.5Hz。电网系统低频振荡的主要原因在于原动机的功率不稳定变化。水轮机组是电力系统的动力来源，水轮机组的稳定出力是确保电力系统平稳运行的关键。水轮机组在运行过程中有可能偏离设计工况，例如，水轮机的水头不等于额定水头时的工况。为了能够消除水轮机组工况的波动导致的低频振荡现象，确保水轮机组的稳定出力，可以利用PID控制技术对水轮机的低频振荡进行控制。但是水轮机组工况变化处于一个非线性状态，传统PID控制技术无法获得比较理想的控制效果。可以将智能算法融入水轮机低频振荡的PID控制之中，从而能够提高水轮机组低频振荡的控制效果。粒子群算法是基于鸟群寻找食物过程提出的随机搜索算法，具有非常好的鲁棒性，能够获得全局最优解，同时具备容易实现和计算效率高的特征。因此，利用粒子算法优化的PID控制技术对水轮机低频振荡进行控制，能够有效地提高水轮机控制的适应性，达到优化控制的目的[1]。

1 水轮机组出力模型

水轮机的输入功率主要是指水轮机水流产生的水力功率，计算公式如下：

式中，ρ表示水的密度，kg/m3；g表示重力加速度，m/s2；Q表示水轮机的流量，m3/s；H表示水轮机的水头，m。

根据相似理论，相似的水轮机有效流量满足如下的关系式：

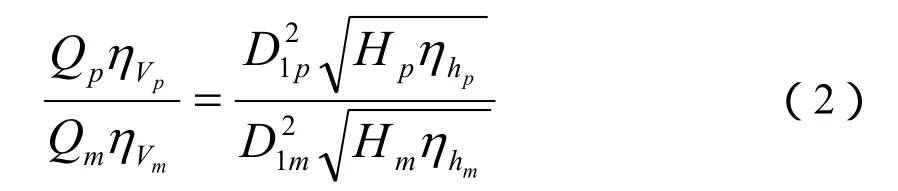
设ηhp=ηhm，ηVp=ηVm，可以得到如下的理论模型：

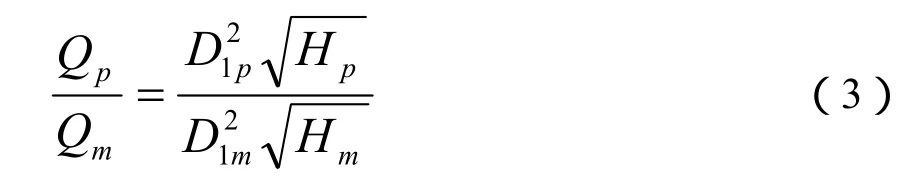
根据式（3）可知，对于相似的水轮机，流量正比于直径的平方，正比于水头的算术平方根。

根据水轮机的出力模型可以推导出以下的数学模型：

设ηhp=ηhm，ηVp=ηVm，ηmp=ηmm，可以获得如下的数学模型：

根据式（5），相似的水轮机，出力正比于直径的平方，正比于水头的3/2次方。

当水轮机的水头偏离额定工况值时，传统的 PID控制无法获得较为理想的控制效果，将导致水轮机组有功功率的波动，因此应该采取改进的PID控制器对其进行控制。

2 PID控制器的基本原理

PID控制器为比例、积分和微分控制器，其主要功能是将控制参数的偏差对应的比例、积分以及微分利用线性组合的方式组成控制量对被控制对象进行控制，PID算法的原理图如图1所示[3]。

PID控制器的时域模型如下所示：

式中，Y(t)表示低频振荡变化的输出；Kp表示比例因子；e(t)表示低频振荡偏差；Ti和Td分别表示积分时间因子和微分时间因子。

图1 PID算法的原理图

在控制水轮机低频振荡时，通常利用数字PID控制器，因此应该利用差分方程离散式（7），可得：

PID控制器的参数优化主要是对式（8）中的Kp、Ti和Td进行优化，传统的优化不能同时兼顾三个参数，从而不能得到最优的控制效果，而粒子群算法可以实现全局优化以及多目标优化，从而能够有效地提高PID控制器的性能。

3 改进粒子群算法的流程

粒子群算法的优化能力较高，所以，应用粒子群算法对 PID控制器的性能参数进行优化是非常重要的。一个基于粒子群算法优化问题的解与搜索空间中一只鸟一一对应，粒子主要是指搜索空间中的所有粒子能够按照适应度函数计算出对应的适应值，此外，每个粒子和一个低频振荡一一对应，适应度以及低频振荡和鸟的飞行方向以及飞行距离一一对应，粒子能够在搜索空间获得全局最优解[4]。

定义D维搜索空间，随机确定一组粒子群，设第i个粒子的位置向量为[4]：

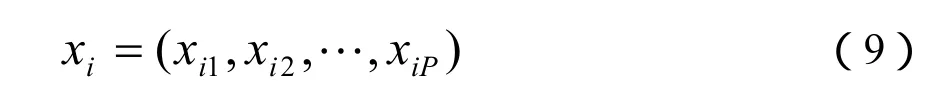
第i个粒子的速度定义为vi，进行粒子群算法迭代运算时，粒子xi可以按照自身的位置以及适应度获得当前的最优位置pre-opti，获得的粒子群可以得到所有粒子的最优位置glo-opti，粒子群算法模型为：

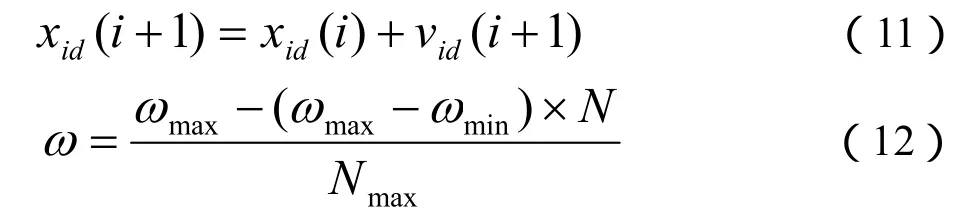
式中，vid(i)表示迭代前的速度，vid(i+1)表示迭代后的速度；xid(i)表示粒子迭代前的位置，xid(i+1)表示粒子迭代后的位置；rand()代表任意数，取值范围为[0，1]；ω代表权重，能够用于算法的全局寻优以及局部寻优；d1和d2均表示粒子群算法的学习因子。粒子算法按照粒子的速度实现寻优，具有较强的记忆能力。

传统的粒子群算法容易陷入早熟，并且寻优效率不高，所以，可以对传统的粒子群算法进行改进，相应的流程如下所示[5]：

（1）初始化粒子群算法的参数；

（2）根据判断发现不在可行搜索空间内的粒子，进行重新的初始化操作；

（3）按照式（10）和式（11）更新粒子群的位置以及速度；

（4）通过判断分析粒子是否超出了自变量的界限，当粒子位置向量中的存在超出可行搜索空间的元素，则从所有粒子群的最优位置向量群中，从全部向量的第j维分量中任意确定一个分量来表示。

（5）判断不同粒子的位置是否满足约束条件，当粒子超出了约束条件，则利用强迫的方法使粒子重新返回可行搜索空间，从而能够保证下次搜索能够得到最优解。

（6）计算可行搜索空间中粒子的适应度，更新粒子的位置以及群体的最优位置。

（7）当算法收敛时，终止迭代运算，否则，返回步骤（3）。

4 水轮机低频振荡控制仿真分析

为了能够验证该改进粒子群算法优化的PID控制的有效性，以某水电站为例进行控制仿真研究，水轮机的额定功率为12050MW，额定水头为12m，实际水头为 50m，额定流量为 130m3/s，机组的飞轮矩为350T·m2。利用PID控制器对水轮机低频振荡进行控制仿真研究，从而能够使水轮机处于稳定的工作状态。水轮机低频振荡PID控制系统的示意图如图2所示。

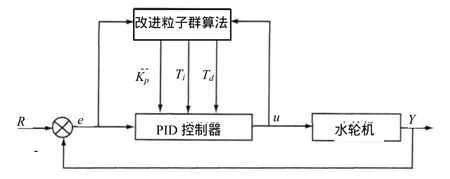
图2 水轮机低频振荡的PID控制系统示意图

改进粒子群算法的参数设置为：种群规模为150，迭代运算的最大值取为200，惯性权值取值范围为[0.1,1]，d1=d2=2.0，PID控制器的参数设置为：Kp=1.2，Ti=0.8，Td=0.20。

为了能够验证改进粒子群算法优化的PID控制器的控制效果，同时利用常规PID控制器和传统粒子群算法优化的PID控制器水轮机低频振荡进行控制仿真分析，仿真程序利用MATLAB软件编制，将三种PID控制器的控制仿真结果进行比较。图3给出了水轮机低频振荡的控制仿真曲线，从仿真曲线可以看出，常规PID控制需要用170次迭代才能进入收敛，传统粒子群算法优化的PID控制器需要80次迭代才能进入收敛，而改进粒子群算法优化的PID控制器只需要40次迭代即可进入收敛，从而表明改进粒子群算放优化的PID控制器具有最快的控制效率。

图3 不同控制器下控制仿真迭代曲线

图4 给出水轮机低频振荡控制的仿真曲线，从图4可以看出，改进粒子群算法优化的PID控制器超调量明显低于传统粒子群算法优化的PID控制器和常规PID控制器的超调量，并且没有明显的数值振荡，从而表明改进粒子群算法优化的PID控制器具有最好的控制效果。

图4 水轮机低频振荡的控制仿真曲线

5 结论

将改进粒子群算法引入到PID控制器，提出了改进粒子群算法优化的PID控制器，由于改进粒子群算法具有较强的全局搜索能力，从而能够提高PID控制器的自适应能力，能够适用于具有非线性特点的水轮机低频振荡的控制之中。通过仿真分析可以看出，改进粒子群算法优化的PID控制器具有较高的控制效率和控制精度。

[1]廖忠． BP网络智能PID控制在水电机组中的应用[J]. 中国计量学院学报, 2006, 3(1)：7-10．

[2]王华强, 石亚娟, 王健波. 神经网络模糊PID在水轮机调速系统中的应用[J]. 合肥工业大学学报(自然科学版), 2012, 35(9): 1187-1192.

[3]胡伟, 徐福缘. 基于改进粒子群算法的PID 控制器参数自整定[J]. 计算机应用研究, 2012, 29(5):1791-1794.

[4]杨智, 陈志堂, 范正平, 等. 基于改进粒子群优化算法的PID控制器整定[J]. 控制理论与应用,2010, 27(10): 1345-1352.