编码器设计与应用的优化

曹颖超，王根义

（1.西安科技大学 计 算机学院，陕西 西 安 7 10054;2.陕西职业技术学院 陕 西 西 安 7 10100）

在现代智能化设备中，编码器应用范围越来越大，但由于社会中一般的应用型人才对编码器知识的缺乏和和对编码器掌握不牢靠，限制了编码器的应用范围。故写此文让基层一般的应用型人才深入掌握编码器知识，提高编码器的应用范围。

1 编码器的概念

一般来说，用文字、符号或者数字表示特定对象的过程都可以叫做编码。日常生活中就经常遇到编码的问题。例如，孩子出生时家长给取名字，在计算机中把一个字符用一个对应的二进制数来表示，给一个地域起一个名称,在计算机中把一个英文字母、数字等字符用一个7位的二进制代码即ASCII来表示，把一个十进制数用BCD来表示等等，都是编码。由于十进制数用电路实现起来比较困难，所以在数字电路中不用它们编码，而是用二进制数进行编码，相应的二进制数叫做二进制代码。编码器就是实现编码操作的电路。用n位二进制代码可以对2n个信号进行编码，把可以表示n位二进制代码的编码电路叫做n位二进制编码器。

2 编码器的设计

以一个2位的二进制编码器的设计为例。

1)编码真值表

一个2位编码器，可以对22＝4个输入变量I3、I2、I1和I0进行编码。输出函数为2位2进制数Y1Y0，这个编码器的真值表如表1所示。

表1 2位编码器编码器真值表Tab1.The truth table of 2 bit encoder

2)输出函数Y1的卡诺图

根据2位的二进制编码器的真值表，可以画出输出函数Y1的卡诺图，如表2所示，其中“×”表示此处的约束行不存在。

表2 输出函数Y1的卡诺图Tab.2 The karnaugh map of output function Y1

3)输出函数Y0的卡诺图如表3所示。

根据2位的二进制编码器的真值表，可以画出输出函数Y1的卡诺图，如表3所示，其中“×”表示此处的约束行不存在。

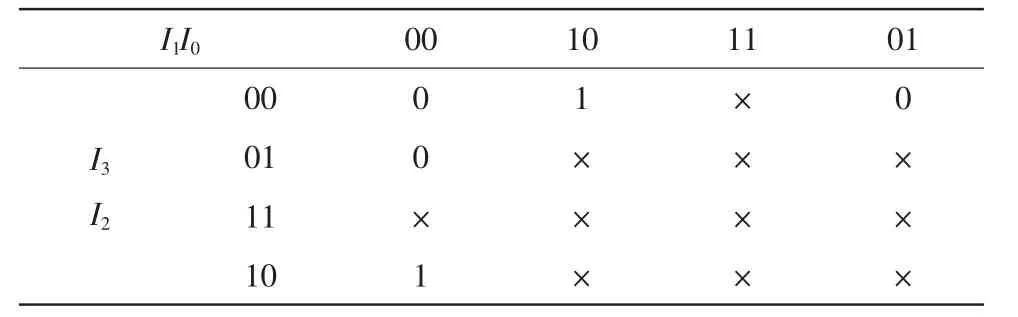
表3 输出函数Y0的卡诺图Tab.3 The karnaugh map of output function Y0

3 编码器的实现

根据输出函数Y1的卡诺图和输出函数Y0的卡诺图，分别化间得出Y1和Y0的最简逻辑表达式如下：

根据Y1和Y0的最简逻辑表达式，就可以用非门、与门和或门来实现这个2位的二进制编码器，画出如图1所示的逻辑图。

当然，实际用的编码器还要解决区分I0～I3均为0、I0为1，I1～I3均为 0、I0～I3中不可能出现两个 1 的情况与 I0～I中至少有两个1这四种种情况。第一种情况，如果I0～I3均为0，即没有任何输入信号，这种情况是很容易区别的 ,只要再添加一个附加的输出变量F，即用Y1的非、Y0的非和I0的非作为一个与门的输出逻辑变量F的输入变量，那么这个逻辑变量F只有在I0～I3均为0时方为1，其余任何情况均为0；第二种情况，如果I0为1，I,1～I3均为0，这种情况属于一种正常普通情况，在这里不需要讨论；第三种情况，I0～I3中不可能出现两个1，即I0～I3这些输入变量互相排斥，这种情况逻辑设计最简单，只要将使逻辑函数值为1的逻辑变量进行逻辑或即可；第四种情况，如果I0～I中至少有两个1，这种情况又可以分为两种情况，一种情况是输入变量出现异常错误情况，可以再添加一个输出逻辑变量予以提示用户，另一种情况是输入变量有这种状态，但要求编码器按照它们的轻重缓急进行排队编码，这在中断系统中是常见现象，这就要求编码器设计者按照输入逻辑变量的编码优先级进行编码设计另外一种编码器，如我们熟悉的8259A芯片。文中如图1所设计的编码器就是针对I0～I中有可能出现两个以上的1的异常错误情况设计的编码器，但没有画出区别I0～I3均为0情况的输出逻辑变量及提示出现异常错误情况的输出逻辑变量的逻辑电路图。

在智能化设备制造中，根据具体情况，如果要求使用的编码器位数比较少，就可以直接用逻辑门来构成，这样往往使用灵活，成本低廉，而且各个方面的性能容易满足。另外一种情况，就是经常要用到的编码器，把它设计好好后制作在一个芯片上，所得到的便是集成编码器，使用非常方便。而且，也可以用位数较少的编码器级联成满足需求的位数较多的编码器。

图1 4线－2线编码器Fig.1 4-2line encoder

4 2位2进优先编码器

1)优先编码的概念

前面讲的编码器，输入信号都是互相排斥的，也就是说在任何时刻,只能对一个输入信号进行编码,不允许有两个和两个以上输入信号同时存在的情况出现,但在优先编码器中则不同，允许几个信号同时输入，但是电路只对其中优先级别最高的进行编码，不理睬级别低的信号，或者说级别低的信号不起作用，这样的电路叫做优先编码器。也就是说，在优先编码器中是优先级别高的信号排斥级别低的，即具有单方面排斥的特性。至于优先级别的高低，则完全是由设计人员根据各个输入信号轻重缓急情况决定的。例如，微机中的I/O接口芯片8259A就用到优先编码器，各个中断源的优先级别还可以由程序员编程规定。

下面以一个2位的二进制优先编码器的设计为例。

2)优先编码真值表

如果我们规定，下列输入信号I3、I2、I1和I0的编码优先级别是I3>I2>I1>I0，则优先编码器的真值表如表4所示。

3)输出函数Y1的卡诺图

根据2位的二进制优先编码器的真值表，可以画出输出函数Y1的卡诺图，如表5所示。

化简卡诺图得，Y1=I3+I2

4)输出函数Y0的卡诺图如表6所示。

根据2位的二进制优先编码器的真值表，可以画出输出函数Y0的卡诺图如表6所示。

化简卡诺图得，Y0=I3+I1

5)优先编码器的实现

根据优先编码器的输出函数Y1的卡诺图和输出函数Y0的卡诺图，分别化间得出Y1和Y0的最简逻辑表达式如下：

用与门很容易实现，画出如图2所示的逻辑图。

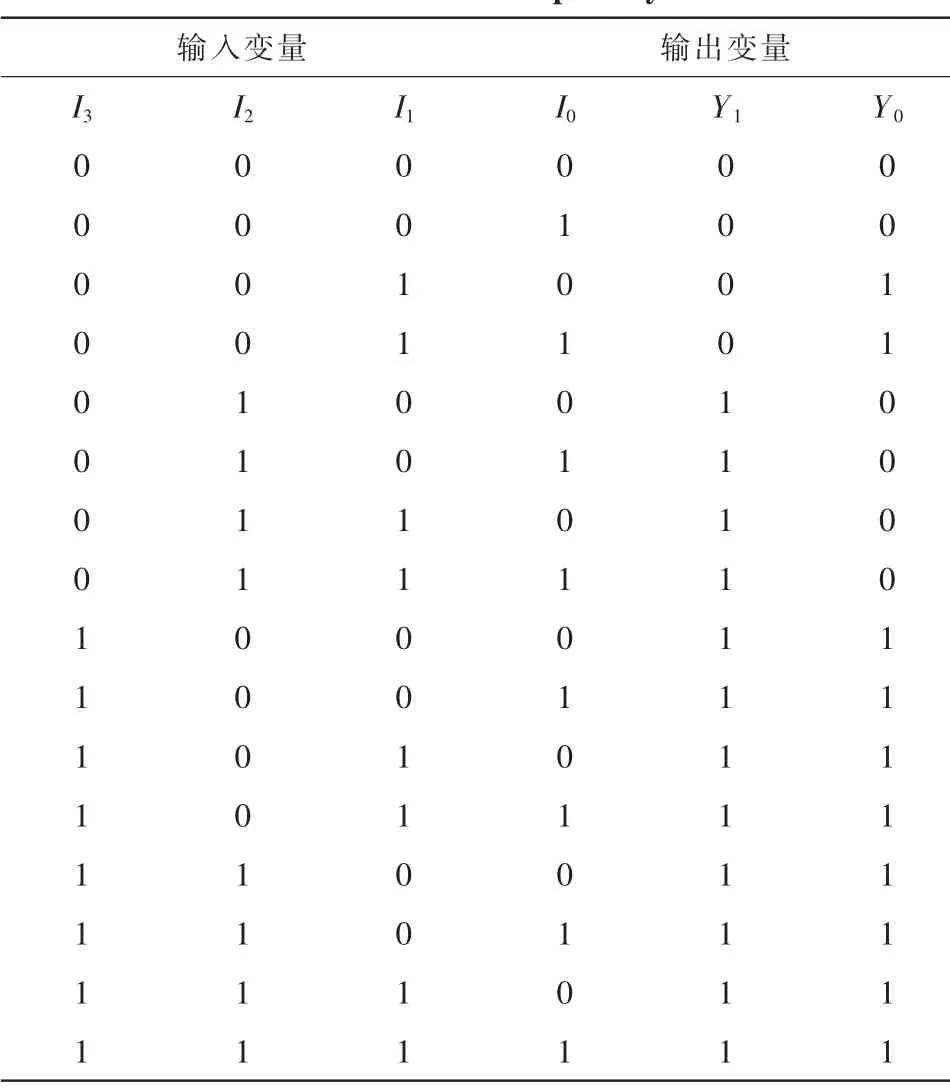
表4 优先编码器真值表Tab.4 The truth table of priority encoder

表5 输出函数Y1的卡诺图Tab.5.The karnaugh map of output function Y1

表6 输出函数Y0的卡诺图Tab.6 The karnaugh map of output function Y0

图2 2位优先编码器的逻辑图Fig.2 The logical diagram of two-bit priority encoder

5 实验

对直接用逻辑门设计制造的编码器和优先编码器，与用集成电路芯片设计制造的编码器和优先编码器进行实验测试，发现在二进制数位相同的条件下，前者比后者成本降低30%，且速度提高1倍，但后者在应用较多，更换较多的场合却比较方便。

6 结论

现在，社会中的智能化设备对编码器的需求量越来越多，大部分编码器的应用者往往因一个简单的编码器而不得不暂时中止手头工作。本论文的创新点，就是提示相关工作人员在一定的条件下可以用几个简单的逻辑门来构成需要的编码器，已解决实际问题。

[1]任为民,沈雅芬数字电子电路学习和实验指导[M]，北京:中央广播电视大学出版社,1993.

[2]康华光.电子技术基础(下册)[M].3版.北京:高等教育出版社,1988.

[3]王晓军.微机原理与接口技术[M].北京，北京邮电大学出版社，2001.

[4]林涛.数字电子技术基础.北京：清华大学出版社，2006.

[5]余孟尝.数字电子技术基础[M].北京：高等教育出版社,1985.

[6]江晓安.数字电子技术[M].2版西安：西安电子科技大学出版社，2001.

[7]刘守义.数字电子技术[M].西安：西安电子科技大学出版社，2003.

[8]吴至友,傅欣欣.无约束全局优化问题的两种新的辅助函数法[J].重庆师范大学学报：自然科学版，2014（5）：1-7.WU Zhi-you;FU Xin-xin.Two new auxiliary function methods of unconstrained global optimization problems[J].Journal of Chongqing Normal University:Natural Science,2014（5）：1-7.

[9]汪颂军,杨健.基于传递函数辨识的双侧频差直流调制抑制研究[J].陕西电力，2014（3）：4-8.WANG Song-jun,YANG Jian.Study on DC Modulation of Bilateral Frequency Difference Based on Transfer Function Identification[J].Shaanxi Electric Power，2014（3）：4-8.