蚁群算法在求解TSP问题中的改进研究
王宝生,屈宝存
(辽宁石油化工大学 辽 宁 抚 顺 1 13001)
旅行商问题(Traveling Salesman Problem,TSP)是一个易于描述却难以处理的NP-HARD问题。近年来,它引起了许多学者的广泛关注。旅行商问题不仅具有很重要的理论价值,而且还具有广泛的实际应用价值,如机器人路径规划、电路板设计、城市管道铺设优化、交通运输以及物流配送等领域都可视为TSP问题的具体应用。对于旅行商问题,目前常用的方法有模拟退火算法、遗传算法、神经网络法等。
蚁群优化算法是模拟自然界中真实蚁群的觅食行为而形成的一种模拟进化算法。它是一种新兴的仿生学优化算法,属于元启发算法的一种。它具有采用分布式并行计算机制、易于与其他方法结合、具有较强的鲁棒性等优点,但其搜索时间长、易陷于局部最优解是其最突出的缺点。因此,既要使得蚁群算法的搜素空间尽可能的大,以寻找那些可能存在最优解的解空间,同时,又要充分利用蚂蚁体内当前所有的有效信息,使得蚁群算法搜索的侧重点放在那些可能具有较高适应值的个体所在的区间内,以较大的概率收敛到全局最优解。因此,在“探索”和“利用”之间建立一个平衡点是蚁群算法研究的关键问题之一。
为了克服蚁群算法的这些缺陷,使它的性能更好,研究者们探索了信息素残留因子(1-ρ)、信息启发式因子、期望启发式因子、信息素强度、蚂蚁数目等蚁群算法的影响因素,并进行了改进[1-3]。高尚提出了混沌蚁群算法,采用混沌初始化改善个体质量和利用混沌扰动避免搜素过程陷入局部极值,实验表明该算法提高了计算效率[4]。汤可宗等从参数的动态调整、信息量的更新规则、局部搜索策略进行相应的改进,引入信息素平滑机制,实验表明该算法具有较好的收敛性和稳定性,能够克服算法中早熟和停滞现象的过早出现[5]。王峰峰等提出了在蚁群算法中植入遗传算法,利用遗传算法生成信息素的分布,克服了蚁群算法中搜索时间长的缺陷,在蚁群算法寻优中,采用交叉和变异的策略改善了TSP解的质量,实验表明该算法是有效的[6]。蔡荣英等提出了迭代改进蚁群算法,在构造解的过程中,蚂蚁始终记忆一个完整的解,并只接受能够改进解的候选城市,使用解的部分重构策略来保持种群的多样性,避免早熟收敛,实验表明该算法在更少的迭代次数中获得更好的解[7]。其他学者也做出了相应的改进研究[8-10]。
文中提出一种改进蚁群算法,该算法在初始位置选择和信息素更新机制两方面进行改进,在相同参数下,改进后的蚁群算法的搜索时间大大缩短,而且得到了更好的最优解。将其应用到旅行商问题中,和其它两种算法相比,其具有较好的搜索最优解的能力,对新解不会过早的终止,探索新解的能力进一步增强。
1 蚁群算法
1.1 蚁群算法的步骤
在求解TSP问题中,蚁群算法的具体实现步骤如下:
1)参数初始化。其中,令时间t=0,循环次数Nc=0,最大循环次数表示为Ncmax;将m个蚂蚁置于n个城市上,则有向图上每条边(i,j)的初始化信息量τij=const,其中const表示常数,且初始时刻△τij=0。
2)循环次数 Nc←Nc+1。
3)蚂蚁的禁忌表索引号k=1。
4)蚂蚁数目k←k+1。
5)蚂蚁根据状态转移概率公式(1.1)计算的概率选择城市 j 并前进
6)修改禁忌表指针,即选则好之后将蚂蚁移动到新的城市,并把该城市移动到该蚂蚁个体的禁忌表中。
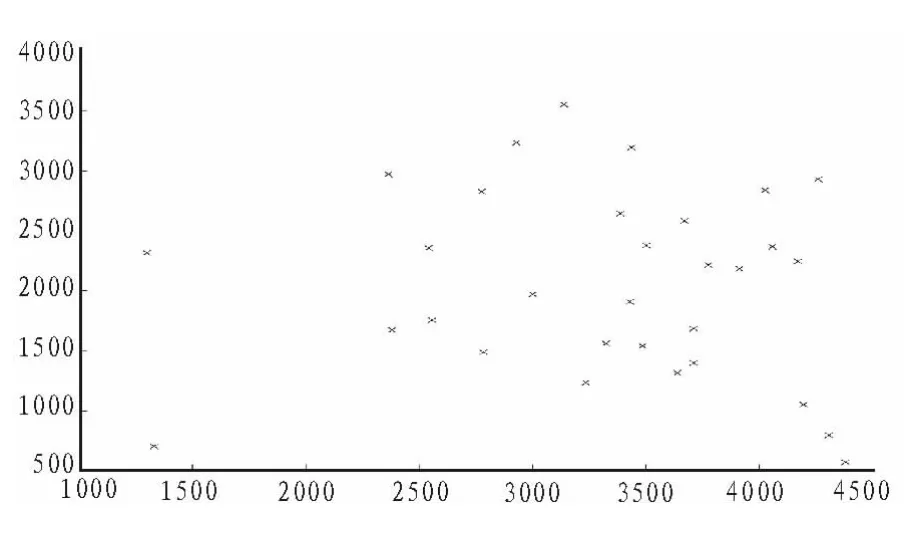
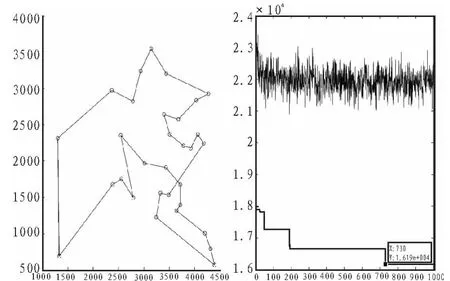
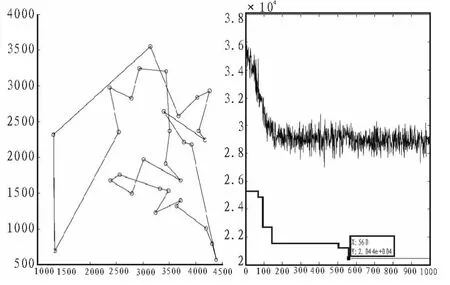
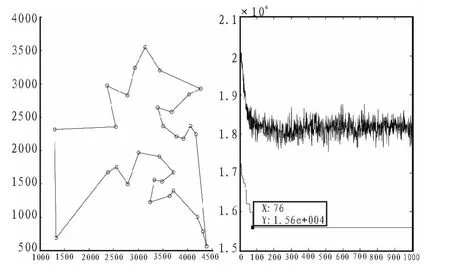
7)若集合C中城市未遍历完,即k 8)根据公式(2)和式(3)更新每条路径上的信息量。 9)若满足结束条件,循环次数Nc>Ncmax,则循环结束并输出程序计算结果,否则清空禁忌表并跳到第2)步。 α为信息启发式因子,表示轨迹的相对重要性,反映了蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用,其值越大,则该蚂蚁越倾向于选择其他蚂蚁经过的路径,蚂蚁之间协作性越强;β为期望启发式因子,表示能见度的相对重要性,反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度,其值越大,则该状态转移概率越接近于贪心规则;ηij(t)为启发函数,其表达式为为相邻两个城市之间的距离。 t+n时刻在路径(i,j)上的信息量按如下规则进行调整 : 式中,ρ为信息素挥发系数,1-ρ为信息素残留因子,为了防止信息的无限积累,ρ的取值范围为次循环中路径(i,j)上的信息素增量,初始时刻为第k只蚂蚁在本次循环中留在路径(i,j)上的信息量。 1)初始位置的缺点 在蚁群算法中,蚂蚁初始位置的选择是随机性的,这样可能造成蚂蚁的分布过于密集。在初始搜索时蚂蚁依据城市间的路径信息来选择下次的搜索路径,使得蚂蚁都倾向于选择在自己附近较短的路径,这样造成了局部收敛过快,得到较小范围的解空间,对求解结果造成影响。 2)在信息素机制方面存在的缺点 ①算法初始化之后,蚂蚁初始化位置是随机选择的,和各个城市间分布了相同的信息素初始浓度,这就造成了算法在开始搜索时的方向不确定性和求解的多样性方面先天不足。 ②在蚂蚁搜索过程中,信息素仅仅在所有蚂蚁完成本次巡游时才会进行全局更新,从而造成搜索时间过长。 由于蚁群算法存在以上的缺点,文中从以上两个方面进行改进,使其全局性与收敛速度都有明显的提高。 对于初始化位置的确定,文中提出一种“蚂蚁边缘化”的初始位置选择策略对初始位置进行优化。 此边缘化的思想是将蚂蚁放在所有城市的边界位置,尽量打散蚂蚁的密集点,这样在初始时刻,蚂蚁相互之间不会过早的影响。判断一个离散区域的边界位置是很困难的,因为它只提供各个城市的坐标信息,这些坐标信息直接可以得到任意两城市的距离信息,这些信息只是一些抽象的数据,对于寻找城市的边界信息是不够的。这里提出一种近似的方法来确定边缘城市。 此方法根据实际城市间距离的数据信息,将某城市和其他城市间的距离信息全部相加和为Si,将Si按照从大到小的次序排列,根据Si的大小判断,最大的Si是离其他城市最远的城市对应的和,其主要思想如下所示: 1)设有m只蚂蚁要选择初始位置,先将n个城市分别求出与其他城市间的距离之和将得到的Si按照从大到小顺序排序; 2)即可确定最大的Si对应的城市即为距离其他城市最远的,其他依次次之; 3)将蚂蚁放在前m个Si对应的城市上,就实现了城市边缘化的选择。 在基本蚁群算法中,分别应用初始位置边缘化和初始位置随机选择,比较2种方法的优劣。此处,城市规模为29,蚂蚁数目为14,最大迭代次数为100,选取10次循环的平均值,α=1,β=5,ρ=0.7。 两种方法的最后结果如表 1 所示。 表1 两种初始化蚂蚁算法的比较Tab.1 The comparison of two kinds of initialization ant algorithm 再次验证蚂蚁数目不同的情况下,两种方法的性能优劣。 城市规模 48,蚂蚁数目分别为 12、24、36、48,最大迭代次数1 000,选取10次循环的平均值,,。应用两种方法的最后结果如表2所示。 表2 不同蚂蚁数目下两种方法的比较Tab.2 The comparison of the two methods under different number of ants 实验结果分析如下: 1)通过表2看出,边缘法比随机法得到了更好的最优解均值,从最优解和最差解的差值可以看出,边缘法的鲁棒性更好。 2)通过表2的对比比较,当蚂蚁数目增加时,边缘法仍然比随机法得到更好的解,但是,两种方法得到的解的差别随着蚂蚁数目的增加越来越小,这是因为,随着蚂蚁的数目增加,越来越多的城市上被放置了蚂蚁,两种方法之间的差异逐渐减小,直到城市数目与蚂蚁数目相同时,两者之间再无差别,同时,算法搜索时间也会随着蚂蚁数目的增多而变长。 由以上分析可知,利用边缘法确定蚂蚁初始化位置确实强于随机方法,对于要巡游的城市规模较大、搜索速率要尽可能快时,可以选择边缘法,同时将蚂蚁数目为城市数目的3/4或者 1/2。 信息素在蚁群算法中的作用关系到算法能够最终顺利找到最优解的关键因素。信息素更新机制为蚂蚁寻找最佳路径提供了指导,对于蚁群算法解决静态组合优化问题和动态组合优化问题这都是非常必要的。 本文对信息素的更新规则做了一些改进。首先,在初始化阶段,对蚂蚁初始化位置和各路径上的信息素初始浓度分布按照某些规则进行分配,使之符合实际情况。其次,将蚂蚁局部的信息素更新和全局信息素更新结合使用,通过精英选择策略,在候选解上的蚂蚁完成一次巡游之后,对它附近路径的信息素就进行更新,其他路径上的信息素不变化。 2.2.1 表格初始化信息素的分配的规范化 利用边缘法可以对蚂蚁初始化位置进行选择,可以考虑将搜索路径上的初始信息素浓度分配按照下述规则进行:在边界的m个城市之间路径上分配相同的信息素τ(0)=c;在余下的路径上根据具体点的位置和求解问题类型的不同,可以通过下述公式确定余下的n-m个点中的某点x处的初始信息素大小: 式中,i是距离城市x处最近的边缘城市位置,k、a均是大于零的常数,若为最小值问题,则a>1;若为最大值问题,则0 k、a的选择应以具体情况而定,即保证算法能够在更接近真实环境下寻优。 2.2.2 蚂蚁全局路径上信息素的改进 在基本的蚁群算法中,蚂蚁只有在一个搜索周期结束后,才能完成一次信息素的更新。对于所有蚂蚁走过的路径,某些路径上可能得到差的解,由于信息素的增加,此解可能变成假的最优解;当最优解还没走过时,该路径的信息素随着蒸发量的变化变得越来越小,从而被忽略。则在下次搜索中,最优解对应的路径被选取的概率越来越小,这样造成了大量无效的搜索,使得运算速度降低。 文中采用以下的信息素更新算法:在全局路径上,假设L(t)是蚂蚁搜索了t次之后所得到的最佳路径,L*(t)是蚂蚁未走过的路径,对所有蚂蚁走过的路径(i,j)∈Lk(t),t次寻优结束后,位置i到j间的路径信息素更新量为△τij(t): 蚂蚁没走过的路径的信息素更新量为: 其中,γ∈(0,1),f(t)为 L(t)对应的最佳目标值。 对于全局蚂蚁走过的路径,信息素的更新规则为: 对于蚂蚁未走过的路径的信息素更新规则为: 此规则减弱了已走过路径的信息素更新速度,避免因为信息素增加过多而导致下次搜索的误判,同时还增强了蚂蚁未到达路径的信息素更新速度,提高了搜素的效率。 以某物流配送中心的VRP系统为例验证算法的效果,假设2辆载货车的载重量8 T,向8个顾客送货,顾客对货物需求量为 gi(i=1,2,…,8),每条配送路径的花费为 Ci,j(i,j=1,2,…,8),可得以下经验数据如表3所示。 表3 物流配送中心配送路线成本表Tab.3 Distribution route cost table of logistics center 对蚁群算法和改进信息素的蚁群算法对上述配送路线进行优化,找到一条最佳的配货路线,即路程最短或者代价最小。 算法中参数设置如下:α=2,β=5,ρ=7,蚂蚁数目 60,迭代10次,实验结果如表4所示。 表4 两种蚁群算法的优化结果比较Tab.4 The comparison of two kinds of ant colony algorithm optimization 改进信息素蚁群算法最后求得的平均最优值是67.5,选择的最优路线是:0-4-7-6-0-1-3-5-8-2-0,这比用基本蚁群算法求解得到的76.5要精确了很多,实验证明改进算法在解决车辆路径寻优问题具有很高的性能。 根据以上思想,该改进的蚁群算法流程可描述如下: 1)参数初始化。其中,令时间t=0,循环次数Nc=0,最大循环次数表示为Ncmax。 根据边缘法初始化蚂蚁位置的思想,将m只蚂蚁放在前m个Si对应的城市上,此时有向图上每条边(i,j)的初始化信息量 τix(0)=ka-f(i-x)。 5)蚂蚁根据状态转移概率公式(1)计算的概率选择城市j并前进 6)修改禁忌表指针,即选则好之后将蚂蚁移动到新的城市,并把该城市移动到该蚂蚁个体的禁忌表中。 7)若集合C中城市未遍历完,即k 8)当所有蚂蚁完成本次搜索后,根据式(5)、(6)、(7)、(8)进行全局信息素更新。 9)若满足结束条件,循环次数Nc>Ncmax,则循环结束并输出程序计算结果,否则清空禁忌表并跳转到第2)步。 为了检验算法的有效性和优越性,分别将基本蚁群算法、遗传算法、改进的蚁群算法应用于31个城市TSP问题中进行仿真实验。其中参数设置为:1)蚁群算法:蚂蚁规模25,最大迭代次数1 000,信息素挥发系数0.7,信息素启发式因子1,期望值因子5。2)遗传算法:种群规模100,最大迭代次数1 000,交叉率0.9,变异率0.1。将TSPLIB31中各个城市的坐标给出,如图1所示。 图1 31个城市的坐标Fig.1 The coordinates of 31 cities 通过仿真得: 1)基本蚁群算法的最短路径,其示意图如图2所示。 图2 基本蚁群算法Fig.2 Basic ant colony algorithm 其最终优化路线为(数字代表TSP31城市坐标的标号):15-1-29-30-31-27-28-26-25-24-20-21-22-18-3-17-19-16-23-11-6-5-4-2-8-9-10-7-13-12-14。 2)遗传算法的最短路径,其示意图如图3所示。 图3 遗传算法最短路径Fig.3 The shortest path of GA 其最终优化路线为: 5-6-9-8-7-3-1-4-15-18-25-27-26-10-11-28-30-29-24-19-23-13-31-14-12-20-21-17-2-16-22。 3)改进的蚁群算法的最短路径,其示意图如图4所示。 图4 改进蚁群算法Fig.4 Improved ant colony algorithm 其最终优化路线为: 14-12-13-11-23-16-5-6-7-2-4-8-9-10-18-1-17-19-3-24-25-20-21-22-26-28-27-30-31-29-15。 通过以上仿真,可以得到表5。 表5 利用几种算法求解TSP31问题的试验结果Tab.5 Experimental results of several algorithms for solving TSP31 分析以上实验数据可见,改进后的蚁群算法具有较好的搜索最优解的能力。如对TSP31在原有蚁群算法上的最短路径为1.619e+004,改进后的算法中得到的最短路径为1.56e+004,在路径演化过程中,改进的算法对新解不会过早的终止,探索新解的能力优化进一步增强。同时,在相同的参数下,改进后的算法不仅迭代次数大大减少、优化时间大大缩短,而且得到了更好的最优解。实验表明,改进后的算法具有较好的性能。 文中在蚁群算法的基础上,通过对初始位置选择、信息素初始化分配和全局信息素三方面的改进,将其应用到求解TSP中,较有效的克服了蚁群算法中出现的搜索时间长、易停滞、收敛速度较慢等问题;从仿真结果来看,该算法在求解性能和时间性能方面都取得了很好的结果,从而实现了TSP问题的优化,为解决一些组合优化问题提供了一定的参考。 [1]Duan H B,Wang D B,Yu X F.Research on the optimum configuration strategy for the adjustable parameters in ant colony algorithm[J].Journal of Communication and Computer,2005,2(9):32-35. [2]叶志伟,郑肇葆.蚁群算法中参数设置的研究-以TSP为例[J].武汉大学学报,2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Research on the ant colony algorithm parameter settings-to TSP Case[J].Wuhan University,2004,29(7):597-601. [3]詹士昌,徐婕,吴俊.蚁群算法中有关算法参数的最优选择[J].科技通报,2003,19(5):381-386.ZHAN Shi-chang,XU Jie,WU Jun.Ant colony algorithm,the optimal choice of algorithm parameters related[J].Technology,2003,19(5):381-386. [4]高尚.解旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005,25(9):100-104.GAO Shang.Chaos ant colony algorithm for traveling salesman problem[J].Systems Engineering Theory and Practice,2005,25(9):100-104. [5]汤可宗,江新姿,张磊,等.一种求解旅行商问题的改进蚁群算法[J].华东理工学院学报,2007,30(4):387-391.TANG Ke-zong,JIANG Xin-zi,ZHANG Lei,et al.Improved ant colony algorithm for solving traveling salesman problem[J].East China Institute of Technology,2007,30(4): 387-391. [6]王峰峰,王仁明,伍佳.求解TSP问题的一种改进蚁群算法[J].控制理论与应用,2010,29(7):1-3.WANG Feng-feng,WANG Ren - ming,WU Jia.TSP problem an improved ant colony algorithm [ J].Control Theory and Applications,2010,29(7):1-3. [7]蔡荣英,王李进,吴超,等.一种求解旅行商问题的迭代改进蚁群优化算法[J].山东大学学报:工学版,2012,42(1):6-11.CAI Rong-ying,WANG Li-jin,WU Chao,et al.Solving Traveling Salesman Problem iterative improvement ACO[J].Shandong University :Engineering Science,2012,42(1):6-11. [8]陈永强.人工蚁群算法及其在组合优化中的应用[D].哈尔滨:哈尔滨工业大学,2003. [9]马良,项培军.蚂蚁算法在组合优化中的应用[J].管理科学学报,2001.4(2):32-36.MA Liang,XIANG Pei-jun.Ant algorithm in combinatorial optimization[J].Journal of Management Sciences,2001.4(2):32-36. [10]叶志伟,郑 葆 .蚁群算法中参数α,β,ρ设置研究-以TSP为例 [ J ].武汉大学学报,2004,29(7):597-601.YE Zhi-wei,ZHENG Zhao-bao.Ant colony algorithm parametersα,β,ρ,set - A case study TSP [J].Wuhan University,2004,29(7):597-601.
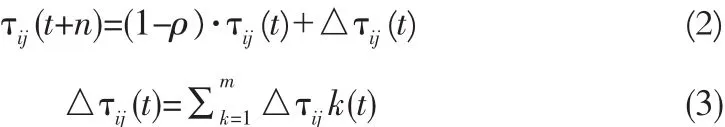
1.2 蚁群算法的缺点
2 改进的蚁群算法
2.1 初始位置选择


2.2 信息素更新规则的改进

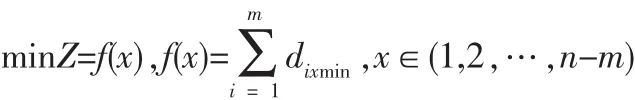

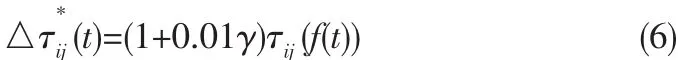




2.3 改进蚁群算法的流程

3 改进蚁群算法在TSP中的应用

4 结论

